DOCSLIB.ORG

Addis Ababa University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Addis Ababa University ADDIS ABABA UNIVERSITY SCHOOL OF GRADUATE STUDIES FACULTY OF BUSINESS AND ECONOMICS ANALYSIS OF FACTORS AFFECTING THE TECHNICAL EFFICIENCY OF COFFEE PRODUCERS IN JIMMA ZONE: A STOCHASTIC FRONTIER ANALYSIS BY ALEMAYEHU ETHIOPIA DEREGE A thesis submitted to the School of Graduate Studies of Addis Ababa University in partial fulfillment of the requirements for the Degree of Master of Science in Economics (Economic Policy Analysis) MAY, 2010 Acknowledgments I am deeply grateful and indebted to Dr Wase Birhanu, my advisor, for answering my big call in short period of time and for his invaluable comments and suggestions. His contributions to this thesis and his profound contribution to my knowledge are very much appreciated in deed. Had it not been for his scrupulous observation, the completion of this paper would have been very difficult. It is impossible to list all names of those individuals who contributed to this thesis. I am extremely indebted to Jimma Zone Agriculture and Rural Development offices for providing me every necessary material and cooperation to my questions. My especial thanks are also due to Professor Tim Coelli, Mr. Badeso Taye, Mr. Qanno Telila, Mr. Hundanol Atnafu, Mr. Gezhany, Jimma zone coffee expert, Mr. Nabsu and Faxxanne for their especial cooperation and help. Above all I am very grateful to super Savior, God for enabling me to fulfill my all dreams in deed. My especial thanks also go to my parents, especially my grandfather Mr. Dareje shube for his moral and financial assistance. Finally, I would like to acknowledge my deep gratitude to African Economic Research Consortium (AERC) for granting the financial assistance to take part in the Joint Facility for Elective Programme in Nairobi, Kenya and for sponsoring my thesis. i Table of Contents Acknowledgments……………………………………………………………………………………………………………………………………i Table of Contents…………………………………………………………………………………………………………………………………….ii List of Tables…………………………………………………………………………………………………………………………………………..iv List of Figures…………………………………………………………………………………………………………………………………………iv List of Appendices………………………………………………………………………………………………………………………………....iv Acronomys and Abbreviations………………………………………………………………………………………………………………..vi Abstract………………………………………………………………………………………………………………………………………………….vii Chapter One: Introduction ............................................................................................................... 1 1.1. Background of the Study ..................................................................................................................... 1 1.2. Statement of the Problem .................................................................................................................... 3 1.3. Objective of the Study ......................................................................................................................... 5 1.4. Hypothesis of the study ....................................................................................................................... 5 1.5. The Scope of the Study ....................................................................................................................... 6 1.6. Significance of the Study .................................................................................................................... 7 1.7 Organization of the Study .................................................................................................................... 8 Chapter Two: Literature Review ...................................................................................................... 9 2.1. Theoretical Literature .......................................................................................................................... 9 2.1.1. Definitions of Efficiency .............................................................................................................. 9 2.1.2. Techniques of Efficiency Measurement ..................................................................................... 12 2.1.3. Approaches for Identifying and Analyzing Determinants of Technical Efficiency ................... 13 2.1.4. The Econometric Approach to Efficiency Measurement ........................................................... 15 2.1.5. The Stochastic Production Frontiers Approach ......................................................................... 17 2.1.5.1. The Normal-Half Stochastic Frontier Model ...................................................................... 19 2.1.5.2. The Exponential and Truncated-Normal Stochastic Frontier Models ................................. 23 2.2. The Empirical Literature ................................................................................................................... 24 Chapter Three: Data and Methodology .......................................................................................... 30 3.1. Background of the Study Area .......................................................................................................... 30 3.2. Data source and Sampling Design .................................................................................................... 31 ii 3.2. 1. Sources of Data ........................................................................................................................ 31 3.2.2. Sampling Design ........................................................................................................................ 32 3.2.3. Data Quality Control and Questionnaire Organization .............................................................. 35 3.3 Methodology of the study .................................................................................................................. 36 3.3.1. Model specification .................................................................................................................... 36 3.3.1.1. The Empirical stochastic frontier model ............................................................................. 37 3.3.1.2. Sources of Technical Inefficiency ....................................................................................... 39 3.3.2. Method of data analysis ............................................................................................................. 41 3.4. Definitions and Measurement (Indicator) of variables used in stochastic and technical inefficiency effects models .......................................................................................................................................... 43 Chapter Four: Results and Discussion ............................................................................................ 50 4.1. Descriptive analysis .......................................................................................................................... 51 4.1.1 Summary statistics of the variables ............................................................................................. 51 4.2. Econometrics Analysis ...................................................................................................................... 54 4.2.1. Hypothesis testing ...................................................................................................................... 56 4.2.2 Effects of Distributional Assumptions on Technical Efficiency Estimates (Model Comparison and Selection) ....................................................................................................................................... 58 4.2.3. Kernel density estimation for the truncated normal distributional assumption .......................... 63 4.2.4 Technical Efficiency: Result from Truncated normal Model ..................................................... 64 4.2.5 Partial Elasticities and Return to Scale ....................................................................................... 64 4.2.6 Technical efficiency of Jimma zone by woreda .......................................................................... 67 4.2.7. Input Utilization, Technical efficiency, Actual and Potential Yield of coffee producers in the Jimma zone .......................................................................................................................................... 69 4.2.8 Analysis of Factors Affecting Technical Inefficiency ................................................................ 71 Chapter Five ................................................................................................................................... 77 5.1 Conclusions and Policy implications ................................................................................................. 77 5.1.1 Summary and conclusions ........................................................................................................... 77 5.1.2 Policy Implications...................................................................................................................... 81 Referances ...................................................................................................................................... 85 List of Appendices .......................................................................................................................... 90 iii List of Tables Table 1 Distribution of Sample households per Woreda ............................................................................. 35 Table 2 Summary statistics and mean difference across technically efficient and inefficient households .. 51 Table 3: Likelihood ratio
Load more

Recommended publications
  • Districts of Ethiopia
    Region District or Woredas Zone Remarks Afar Region Argobba Special Woreda -- Independent district/woredas Afar Region Afambo Zone 1 (Awsi Rasu) Afar Region Asayita Zone 1 (Awsi Rasu) Afar Region Chifra Zone 1 (Awsi Rasu) Afar Region Dubti Zone 1 (Awsi Rasu) Afar Region Elidar Zone 1 (Awsi Rasu) Afar Region Kori Zone 1 (Awsi Rasu) Afar Region Mille Zone 1 (Awsi Rasu) Afar Region Abala Zone 2 (Kilbet Rasu) Afar Region Afdera Zone 2 (Kilbet Rasu) Afar Region Berhale Zone 2 (Kilbet Rasu) Afar Region Dallol Zone 2 (Kilbet Rasu) Afar Region Erebti Zone 2 (Kilbet Rasu) Afar Region Koneba Zone 2 (Kilbet Rasu) Afar Region Megale Zone 2 (Kilbet Rasu) Afar Region Amibara Zone 3 (Gabi Rasu) Afar Region Awash Fentale Zone 3 (Gabi Rasu) Afar Region Bure Mudaytu Zone 3 (Gabi Rasu) Afar Region Dulecha Zone 3 (Gabi Rasu) Afar Region Gewane Zone 3 (Gabi Rasu) Afar Region Aura Zone 4 (Fantena Rasu) Afar Region Ewa Zone 4 (Fantena Rasu) Afar Region Gulina Zone 4 (Fantena Rasu) Afar Region Teru Zone 4 (Fantena Rasu) Afar Region Yalo Zone 4 (Fantena Rasu) Afar Region Dalifage (formerly known as Artuma) Zone 5 (Hari Rasu) Afar Region Dewe Zone 5 (Hari Rasu) Afar Region Hadele Ele (formerly known as Fursi) Zone 5 (Hari Rasu) Afar Region Simurobi Gele'alo Zone 5 (Hari Rasu) Afar Region Telalak Zone 5 (Hari Rasu) Amhara Region Achefer -- Defunct district/woredas Amhara Region Angolalla Terana Asagirt -- Defunct district/woredas Amhara Region Artuma Fursina Jile -- Defunct district/woredas Amhara Region Banja -- Defunct district/woredas Amhara Region Belessa --
    [Show full text]
  • Challenges of Clinical Chemistry Analyzers Utilization in Public Hospital Laboratories of Selected Zones of Oromia Region, Ethiopia: a Mixed Methods Study
    Research Article ISSN: 2574 -1241 DOI: 10.26717/BJSTR.2021.34.005584 Challenges of Clinical Chemistry Analyzers Utilization in Public Hospital Laboratories of Selected Zones of Oromia Region, Ethiopia: A Mixed Methods Study Rebuma Belete1*, Waqtola Cheneke2, Aklilu Getachew2 and Ahmedmenewer Abdu1 1Department of Medical Laboratory Sciences, College of Health and Medical Sciences, Haramaya University, Harar, Ethiopia 2School of Medical Laboratory Sciences, Faculty of Health Sciences, Institute of Health, Jimma University, Jimma, Ethiopia *Corresponding author: Rebuma Belete, Department of Medical Laboratory Sciences, College of Health and Medical Sciences, Haramaya University, Harar, Ethiopia ARTICLE INFO ABSTRACT Received: March 16, 2021 Background: The modern practice of clinical chemistry relies ever more heavily on automation technologies. Their utilization in clinical laboratories in developing countries Published: March 22, 2021 is greatly affected by many factors. Thus, this study was aimed to identify challenges affecting clinical chemistry analyzers utilization in public hospitals of selected zones of Oromia region, Ethiopia. Citation: Rebuma Belete, Waqtola Cheneke, Aklilu Getachew, Ahmedmenew- Methods: A cross-sectional study using quantitative and qualitative methods er Abdu. Challenges of Clinical Chemistry was conducted in 15 public hospitals from January 28 to March 15, 2019. Purposively Analyzers Utilization in Public Hospital selected 68 informants and 93 laboratory personnel working in clinical chemistry section Laboratories of Selected Zones of Oromia were included in the study. Data were collected by self-administered questionnaires, Region, Ethiopia: A Mixed Methods Study. in-depth interviews and observational checklist. The quantitative data were analyzed Biomed J Sci & Tech Res 34(4)-2021. by descriptive statistics using SPSS 25.0 whereas qualitative data was analyzed by a BJSTR.
    [Show full text]
  • Historical Survey of Limmu Genet Town from Its Foundation up to Present
    INTERNATIONAL JOURNAL OF SCIENTIFIC & TECHNOLOGY RESEARCH VOLUME 6, ISSUE 07, JULY 2017 ISSN 2277-8616 Historical Survey Of Limmu Genet Town From Its Foundation Up To Present Dagm Alemayehu Tegegn Abstract: The process of modern urbanization in Ethiopia began to take shape since the later part of the nineteenth century. The territorial expansion of emperor Menelik (r. 1889 –1913), political stability and effective centralization and bureaucratization of government brought relative acceleration of the pace of urbanization in Ethiopia; the improvement of the system of transportation and communication are identified as factors that contributed to this new phase of urban development. Central government expansion to the south led to the appearance of garrison centers which gradually developed to small- sized urban center or Katama. The garrison were established either on already existing settlements or on fresh sites and also physically they were situated on hill tops. Consequently, Limmu Genet town was founded on the former Limmu Ennarya state‘s territory as a result of the territorial expansion of the central government and system of administration. Although the history of the town and its people trace many year back to the present, no historical study has been conducted on. Therefore the aim of this study is to explore the history of Limmu Genet town from its foundation up to present. Keywords: Limmu Ennary, Limmu Genet, Urbanization, Development ———————————————————— 1. Historical Background of the Study Area its production. The production and marketing of forest coffee spread the fame and prestige of Limmu Enarya ( The early history of Limmu Oromo Mohammeed Hassen, 1994). The name Limmu Ennarya is The history of Limmu Genet can be traced back to the rise derived from a combination of the name of the medieval of the Limmu Oromo clans, which became kingdoms or state of Ennarya and the Oromo clan name who settled in states along the Gibe river basin.
    [Show full text]
  • (Coffea Arabica L.) Accessions Collected from Limmu Coffee
    American Journal of BioScience 2021; 9(3): 79-85 http://www.sciencepublishinggroup.com/j/ajbio doi: 10.11648/j.ajbio.20210903.12 ISSN: 2330-0159 (Print); ISSN: 2330-0167 (Online) Phenotypic Diversity of Ethiopian Coffee ( Coffea arabica L.) Accessions Collected from Limmu Coffee Growing Areas Using Multivariate Analysis Lemi Beksisa *, Tadesse Benti, Getachew Weldemichael Ethiopian Institute of Agricultural Research, Jimma Agricultural Research Center, Jimma, Ethiopia Email address: *Corresponding author To cite this article: Lemi Beksisa, Tadesse Benti, Getachew Weldemichael. Phenotypic Diversity of Ethiopian Coffee ( Coffea arabica L.) Accessions Collected from Limmu Coffee Growing Areas Using Multivariate Analysis. American Journal of BioScience . Vol. 9, No. 3, 2021, pp. 79-85. doi: 10.11648/j.ajbio.20210903.12 Received : April 17, 2021; Accepted : May 11, 2021; Published : May 20, 2021 Abstract: Forty seven Coffea arabica L. germplasm accessions collected from Limmu district were field evaluated from 2004/5 to 2013/14 with two commercial check varieties at Agaro Agricultural Research sub center in single plot. The objective of the experiment was to assess the variability among the accessions using quantitative traits. Data for about eight quantitative traits were recorded only once in experimental period, while the yield data were recorded for six consecutive cropping seasons. Cluster, genetic divergence, and principal component analysis were used to assess the variability among the genotypes. The results revealed that average linkage cluster analysis for nine traits grouped the germplasm accessions in to three clusters. The number of accessions per cluster ranged from three in cluster III to 25 in cluster II. The clustering pattern of the coffee accessions revealed that the prevalence of moderate genetic diversity in Limmu coffee for the characters studied.
    [Show full text]
  • Oromia Region Administrative Map(As of 27 March 2013)
    ETHIOPIA: Oromia Region Administrative Map (as of 27 March 2013) Amhara Gundo Meskel ! Amuru Dera Kelo ! Agemsa BENISHANGUL ! Jangir Ibantu ! ! Filikilik Hidabu GUMUZ Kiremu ! ! Wara AMHARA Haro ! Obera Jarte Gosha Dire ! ! Abote ! Tsiyon Jars!o ! Ejere Limu Ayana ! Kiremu Alibo ! Jardega Hose Tulu Miki Haro ! ! Kokofe Ababo Mana Mendi ! Gebre ! Gida ! Guracha ! ! Degem AFAR ! Gelila SomHbo oro Abay ! ! Sibu Kiltu Kewo Kere ! Biriti Degem DIRE DAWA Ayana ! ! Fiche Benguwa Chomen Dobi Abuna Ali ! K! ara ! Kuyu Debre Tsige ! Toba Guduru Dedu ! Doro ! ! Achane G/Be!ret Minare Debre ! Mendida Shambu Daleti ! Libanos Weberi Abe Chulute! Jemo ! Abichuna Kombolcha West Limu Hor!o ! Meta Yaya Gota Dongoro Kombolcha Ginde Kachisi Lefo ! Muke Turi Melka Chinaksen ! Gne'a ! N!ejo Fincha!-a Kembolcha R!obi ! Adda Gulele Rafu Jarso ! ! ! Wuchale ! Nopa ! Beret Mekoda Muger ! ! Wellega Nejo ! Goro Kulubi ! ! Funyan Debeka Boji Shikute Berga Jida ! Kombolcha Kober Guto Guduru ! !Duber Water Kersa Haro Jarso ! ! Debra ! ! Bira Gudetu ! Bila Seyo Chobi Kembibit Gutu Che!lenko ! ! Welenkombi Gorfo ! ! Begi Jarso Dirmeji Gida Bila Jimma ! Ketket Mulo ! Kersa Maya Bila Gola ! ! ! Sheno ! Kobo Alem Kondole ! ! Bicho ! Deder Gursum Muklemi Hena Sibu ! Chancho Wenoda ! Mieso Doba Kurfa Maya Beg!i Deboko ! Rare Mida ! Goja Shino Inchini Sululta Aleltu Babile Jimma Mulo ! Meta Guliso Golo Sire Hunde! Deder Chele ! Tobi Lalo ! Mekenejo Bitile ! Kegn Aleltu ! Tulo ! Harawacha ! ! ! ! Rob G! obu Genete ! Ifata Jeldu Lafto Girawa ! Gawo Inango ! Sendafa Mieso Hirna
    [Show full text]
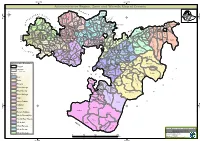
  • Administrative Region, Zone and Woreda Map of Oromia a M Tigray a Afar M H U Amhara a Uz N M
    35°0'0"E 40°0'0"E Administrative Region, Zone and Woreda Map of Oromia A m Tigray A Afar m h u Amhara a uz N m Dera u N u u G " / m r B u l t Dire Dawa " r a e 0 g G n Hareri 0 ' r u u Addis Ababa ' n i H a 0 Gambela m s Somali 0 ° b a K Oromia Ü a I ° o A Hidabu 0 u Wara o r a n SNNPR 0 h a b s o a 1 u r Abote r z 1 d Jarte a Jarso a b s a b i m J i i L i b K Jardega e r L S u G i g n o G A a e m e r b r a u / K e t m uyu D b e n i u l u o Abay B M G i Ginde e a r n L e o e D l o Chomen e M K Beret a a Abe r s Chinaksen B H e t h Yaya Abichuna Gne'a r a c Nejo Dongoro t u Kombolcha a o Gulele R W Gudetu Kondole b Jimma Genete ru J u Adda a a Boji Dirmeji a d o Jida Goro Gutu i Jarso t Gu J o Kembibit b a g B d e Berga l Kersa Bila Seyo e i l t S d D e a i l u u r b Gursum G i e M Haro Maya B b u B o Boji Chekorsa a l d Lalo Asabi g Jimma Rare Mida M Aleltu a D G e e i o u e u Kurfa Chele t r i r Mieso m s Kegn r Gobu Seyo Ifata A f o F a S Ayira Guliso e Tulo b u S e G j a e i S n Gawo Kebe h i a r a Bako F o d G a l e i r y E l i Ambo i Chiro Zuria r Wayu e e e i l d Gaji Tibe d lm a a s Diga e Toke n Jimma Horo Zuria s e Dale Wabera n a w Tuka B Haru h e N Gimbichu t Kutaye e Yubdo W B Chwaka C a Goba Koricha a Leka a Gidami Boneya Boshe D M A Dale Sadi l Gemechis J I e Sayo Nole Dulecha lu k Nole Kaba i Tikur Alem o l D Lalo Kile Wama Hagalo o b r Yama Logi Welel Akaki a a a Enchini i Dawo ' b Meko n Gena e U Anchar a Midega Tola h a G Dabo a t t M Babile o Jimma Nunu c W e H l d m i K S i s a Kersana o f Hana Arjo D n Becho A o t
    [Show full text]
  • Factors Affecting Social Accountability in Service Providing Public Sectors: Exploring Beneficiaries' Perspectiv Es in Jimma Z
    Research, Society and Development ISSN: 2525-3409 ISSN: 2525-3409 [email protected] Universidade Federal de Itajubá Brasil Factors Affecting Social Accountability in Service Providing Public Sectors: Exploring Beneficiaries’ Perspectiv es in Jimma Zone Doja, Hunde; Duressa, Tadele Factors Affecting Social Accountability in Service Providing Public Sectors: Exploring Beneficiaries’ Perspectiv es in Jimma Zone Research, Society and Development, vol. 8, no. 12, 2019 Universidade Federal de Itajubá, Brasil Available in: https://www.redalyc.org/articulo.oa?id=560662203013 DOI: https://doi.org/10.33448/rsd-v8i12.1571 This work is licensed under Creative Commons Attribution 4.0 International. PDF generated from XML JATS4R by Redalyc Project academic non-profit, developed under the open access initiative Factors Affecting Social Accountability in Service Providing Public Sectors: Exploring Beneficiaries’ Perspectiv es in Jimma Zone Fatores que afetam a responsabilidade social nos setores prestadores de serviços: explorando as perspectivas dos beneficiários na zona de Jimma Factores que afectan la responsabilidad social en la prestación de servicios a sectores públicos: exploración de las perspectivas de los beneficiarios en la zona de Jimma Hunde Doja [email protected] Jimma University, Etiopía hp://orcid.org/0000-0002-1559-6252 Tadele Duressa [email protected] Jimma University, Etiopía Research, Society and Development, vol. 8, no. 12, 2019 hp://orcid.org/0000-0002-8663-1027 Universidade Federal de Itajubá, Brasil Received: 29 August 2019 Revised: 31 August 2019 Accepted: 25 September 2019 Abstract: is study was undertaken to identify the factors affecting social Published: 27 September 2019 accountability in service providing public sector organizations from beneficiary DOI: https://doi.org/10.33448/rsd- perspectives in Jimma Zone.
    [Show full text]
  • Ethiopia: the State of the World's Forest Genetic Resources
    ETHIOPIA This country report is prepared as a contribution to the FAO publication, The Report on the State of the World’s Forest Genetic Resources. The content and the structure are in accordance with the recommendations and guidelines given by FAO in the document Guidelines for Preparation of Country Reports for the State of the World’s Forest Genetic Resources (2010). These guidelines set out recommendations for the objective, scope and structure of the country reports. Countries were requested to consider the current state of knowledge of forest genetic diversity, including: Between and within species diversity List of priority species; their roles and values and importance List of threatened/endangered species Threats, opportunities and challenges for the conservation, use and development of forest genetic resources These reports were submitted to FAO as official government documents. The report is presented on www. fao.org/documents as supportive and contextual information to be used in conjunction with other documentation on world forest genetic resources. The content and the views expressed in this report are the responsibility of the entity submitting the report to FAO. FAO may not be held responsible for the use which may be made of the information contained in this report. THE STATE OF FOREST GENETIC RESOURCES OF ETHIOPIA INSTITUTE OF BIODIVERSITY CONSERVATION (IBC) COUNTRY REPORT SUBMITTED TO FAO ON THE STATE OF FOREST GENETIC RESOURCES OF ETHIOPIA AUGUST 2012 ADDIS ABABA IBC © Institute of Biodiversity Conservation (IBC)
    [Show full text]
  • Ethiopia Administrative Map As of 2013
    (as of 27 March 2013) ETHIOPIA:Administrative Map R E Legend E R I T R E A North D Western \( Erob \ Tahtay Laelay National Capital Mereb Ahferom Gulomekeda Adiyabo Adiyabo Leke Central Ganta S Dalul P Afeshum Saesie Tahtay Laelay Adwa E P Tahtay Tsaedaemba Regional Capital Kafta Maychew Maychew Koraro Humera Asgede Werei Eastern A Leke Hawzen Tsimbila Medebay Koneba Zana Kelete Berahle Western Atsbi International Boundary Welkait Awelallo Naeder Tigray Wenberta Tselemti Adet Kola Degua Tsegede Temben Mekele Temben P Zone 2 Undetermined Boundary Addi Tselemt Tanqua Afdera Abergele Enderta Arekay Ab Ala Tsegede Beyeda Mirab Armacho Debark Hintalo Abergele Saharti Erebti Regional Boundary Wejirat Tach Samre Megale Bidu Armacho Dabat Janamora Alaje Lay Sahla Zonal Boundary Armacho Wegera Southern Ziquala Metema Sekota Endamehoni Raya S U D A N North Wag Azebo Chilga Yalo Amhara East Ofla Teru Woreda Boundary Gonder West Belesa Himra Kurri Gonder Dehana Dembia Belesa Zuria Gaz Alamata Zone 4 Quara Gibla Elidar Takusa I Libo Ebenat Gulina Lake Kemkem Bugna Kobo Awra Afar T Lake Tana Lasta Gidan (Ayna) Zone 1 0 50 100 200 km Alfa Ewa U Fogera North Farta Lay Semera ¹ Meket Guba Lafto Semen Gayint Wollo P O Dubti Jawi Achefer Bahir Dar East Tach Wadla Habru Chifra B G U L F O F A D E N Delanta Aysaita Creation date:27 Mar.2013 P Dera Esite Gayint I Debub Bahirdar Ambasel Dawunt Worebabu Map Doc Name:21_ADM_000_ETH_032713_A0 Achefer Zuria West Thehulederie J Dangura Simada Tenta Sources:CSA (2007 population census purpose) and Field Pawe Mecha
    [Show full text]
  • Annual Report 2019
    >> ANNUAL REPORT, PROJECT 200452, MARCH 31ST, 2020 ANNUAL REPORT 2019 STRENGTHENING THE HEALTH SYSTEM IN JIMMA ZONE (OROMIA REGION, ETHIOPIA) THROUGH PERFORMANCE BASED FINANCING (2019-2023) MARCH 31ST, 2020, THE HAGUE, THE NETHERLANDS INGE BARMENTLO POLITE DUBE MOSES MUNYUMAHORO MAARTEN ORANJE CARMEN SCHAKEL ANNUAL REPORT 2019 - STRENGTHENING THE HEALTH SYSTEM IN JIMMA ZONE, ETHIOPIA MARCH 2020 © CORDAID 2 ANNUAL REPORT 2019 - STRENGTHENING THE HEALTH SYSTEM IN JIMMA ZONE, ETHIOPIA TABLE OF CONTENTS LIST OF ABBREVIATIONS ................................................................................................ 4 EXECUTIVE SUMMARY ..................................................................................................... 5 PROJECT BACKGROUND ................................................................................................. 8 1. OUTCOME 1: IMPROVED HEALTH SERVICE DELIVERY ........................................... 9 2. OUTCOME 2: IMPROVED GOVERNANCE OF HEALTH SERVICE DELIVERY ......... 57 3. OUTCOME 3: AN ENHANCED HEALTH INFORMATION SYSTEM............................ 61 CONCLUSIONS ................................................................................................................ 63 ANNEXES ......................................................................................................................... 66 Annex 1: Theory of Change (From: Original Proposal PBF Jimma Zone, October 2018)................. 67 Annex 2: Logical Framework (From: Original Proposal PBF Jimma Zone, October 2018)
    [Show full text]
  • Trypanosome Infection Rate in Glossina
    Trypanosome Infection Rate in Glossina tachinoides: Infested Rivers of Limmu Kosa District Jimma Zone, Western Ethiopia behablom meharenet ( [email protected] ) kality tsetse ies mass rearing and irradiation center https://orcid.org/0000-0002-3080-1541 Dereje Alemu national institute for controle and erradication of tstse y and trypanosomosis Research note Keywords: Limmu Kosa District, Trypanosome, Infection Rate, Glossina tachinoides Posted Date: January 24th, 2020 DOI: https://doi.org/10.21203/rs.2.14379/v3 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Version of Record: A version of this preprint was published at BMC Research Notes on March 5th, 2020. See the published version at https://doi.org/10.1186/s13104-020-04970-1. Page 1/8 Abstract Objective : Trypanosomosis is a disease of domestic animals and humans resulting from infection with parasitaemic protozoa of the genus Trypanosoma transmitted primarily by tsetse ies. A cross-sectional study was conducted from January-March 2018, to estimate the infection rate of trypanosome in Glossina tachinoides , their distribution, magnitude and involved trypanosome species in Limmu Kosa District of Jimma zone. Methodology and result : Study methodology involved entomological survey using monoconical traps to study the magnitude of Fly density Flay/Trap/Day (FTD) and tsetse y dissection to estimate infection rate of trypanosome in vector ies. The study result indicated that there was only one species of Tsetse y Glossina tachinoides detected with FTD=4.45. From total of (n=284) dissected Glossina tachinoides ies only (n= 5) positive for Trypanosome resulting in 1.76% Infection Rate.
    [Show full text]
  • Annual Report IOM PRESENCE in ETHIOPIA IOM Presence in Ethiopia ETHIOPIA: Administrative Map (As of 14 January 2011)
    IOM Ethiopia 2018Annual Report IOM PRESENCE IN ETHIOPIA IOM Presence in Ethiopia ETHIOPIA: Administrative Map (as of 14 January 2011) R ShireERITREA E Legend Tahtay Erob Laelay Adiyabo Mereb Ahferom Gulomekeda \\( Adiyabo Leke D National Capital Ganta Medebay Dalul North Adwa Afeshum Saesie Tahtay Zana Laelay Tsaedaemba Kafta Western Maychew PP Koraro Central Humera Asgede Tahtay Eastern Regional Capital Naeder Werei Hawzen Western Tsimbila Maychew Adet Leke Koneba Berahle Welkait Kelete Atsbi S Tigray Awelallo Wenberta International Boundary Tselemti Kola Degua Tsegede Mekele E Temben Temben P Addi Tselemt Tanqua Afdera Zone 2 Enderta Arekay Abergele Regional Boundary Tsegede Beyeda Ab Ala MRCMirab Saharti A Armacho Debark Samre Hintalo Erebti Abergele Wejirat Tach Megale Bidu Zonal Boundary Armacho Dabat Janamora Alaje Lay Sahla North Armacho Wegera Southern Ziquala Woreda Boundary Metema Gonder Sekota Endamehoni Raya Wag Azebo Chilga Yalo Amhara East Ofla Teru West Belesa Himra Kurri Gonder Dehana Belesa Lake Dembia Zuria Gaz Alamata Zone 4 Quara Gibla Semera Elidar Takusa Libo Ebenat Gulina Kemkem Bugna Lasta Kobo Awra Afar Gidan Lake Tana South (Ayna) 0 50 100 200 km Ewa Alfa Fogera Gonder North ¹ Lay Zone 1 Farta Meket Guba Lafto Dubti Gayint MRC Asayta Semen Wollo P Jawi Achefer Tach Habru Chifra Bahr Dar East Wadla Delanta G U L F O F A D E N P Gayint Aysaita Creation date:14 Jan.2011 Dera Esite Bahirdar Ambasel Map Doc Name:21_ADM_000_ETH_011411_A0 Debub Zuria Dawunt Worebabu Achefer West Sources:CSA,EMA Dangura Pawe Esite Simada Tenta Adaa'r Mile Mecha Yilmana Afambo Guba Special Kutaber Feedback:[email protected] http;//ochaonline.un.org/ethiopia Dangila Densa Mekdela Bati DJIBOUTI SUDAN Metekel West Thehulederie The boundaries and names shown and the designations used on Telalak Fagta Lakoma Gonje ADDIS ABABADessie Gojam Sayint Zuria Kalu this map do not imply official endorsement or acceptance by the Sirba Mandura Hulet Goncha South Zone Sekela Quarit Mehal Asossa Abay Banja Dega Ej Enese Siso Argoba United Nations.
    [Show full text]