Fracture Mechanics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

10-1 CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams And
EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy CHAPTER 10 DEFORMATION 10.1 Stress-Strain Diagrams and Material Behavior 10.2 Material Characteristics 10.3 Elastic-Plastic Response of Metals 10.4 True stress and strain measures 10.5 Yielding of a Ductile Metal under a General Stress State - Mises Yield Condition. 10.6 Maximum shear stress condition 10.7 Creep Consider the bar in figure 1 subjected to a simple tension loading F. Figure 1: Bar in Tension Engineering Stress () is the quotient of load (F) and area (A). The units of stress are normally pounds per square inch (psi). = F A where: is the stress (psi) F is the force that is loading the object (lb) A is the cross sectional area of the object (in2) When stress is applied to a material, the material will deform. Elongation is defined as the difference between loaded and unloaded length ∆푙 = L - Lo where: ∆푙 is the elongation (ft) L is the loaded length of the cable (ft) Lo is the unloaded (original) length of the cable (ft) 10-1 EN380 Naval Materials Science and Engineering Course Notes, U.S. Naval Academy Strain is the concept used to compare the elongation of a material to its original, undeformed length. Strain () is the quotient of elongation (e) and original length (L0). Engineering Strain has no units but is often given the units of in/in or ft/ft. ∆푙 휀 = 퐿 where: is the strain in the cable (ft/ft) ∆푙 is the elongation (ft) Lo is the unloaded (original) length of the cable (ft) Example Find the strain in a 75 foot cable experiencing an elongation of one inch. -

6. Fracture Mechanics
6. Fracture mechanics lead author: J, R. Rice Division of Applied Sciences, Harvard University, Cambridge MA 02138 Reader's comments on an earlier draft, prepared in consultation with J. W. Hutchinson, C. F. Shih, and the ASME/AMD Technical Committee on Fracture Mechanics, pro vided by A. S. Argon, S. N. Atluri, J. L. Bassani, Z. P. Bazant, S. Das, G. J. Dvorak, L. B. Freund, D. A. Glasgow, M. F. Kanninen, W. G. Knauss, D. Krajcinovic, J D. Landes, H. Liebowitz, H. I. McHenry, R. O. Ritchie, R. A. Schapery, W. D. Stuart, and R. Thomson. 6.0 ABSTRACT Fracture mechanics is an active research field that is currently advancing on many fronts. This appraisal of research trends and opportunities notes the promising de velopments of nonlinear fracture mechanics in recent years and cites some of the challenges in dealing with topics such as ductile-brittle transitions, failure under sub stantial plasticity or creep, crack tip processes under fatigue loading, and the need for new methodologies for effective fracture analysis of composite materials. Continued focus on microscale fracture processes by work at the interface of solid mechanics and materials science holds promise for understanding the atomistics of brittle vs duc tile response and the mechanisms of microvoid nucleation and growth in various ma terials. Critical experiments to characterize crack tip processes and separation mecha nisms are a pervasive need. Fracture phenomena in the contexts of geotechnology and earthquake fault dynamics also provide important research challenges. 6.1 INTRODUCTION cracking in the more brittle structural materials such as high strength metal alloys. -

Crack Tip Elements and the J Integral
EN234: Computational methods in Structural and Solid Mechanics Homework 3: Crack tip elements and the J-integral Due Wed Oct 7, 2015 School of Engineering Brown University The purpose of this homework is to help understand how to handle element interpolation functions and integration schemes in more detail, as well as to explore some applications of FEA to fracture mechanics. In this homework you will solve a simple linear elastic fracture mechanics problem. You might find it helpful to review some of the basic ideas and terminology associated with linear elastic fracture mechanics here (in particular, recall the definitions of stress intensity factor and the nature of crack-tip fields in elastic solids). Also check the relations between energy release rate and stress intensities, and the background on the J integral here. 1. One of the challenges in using finite elements to solve a problem with cracks is that the stress field at a crack tip is singular. Standard finite element interpolation functions are designed so that stresses remain finite a everywhere in the element. Various types of special b c ‘crack tip’ elements have been designed that 3L/4 incorporate the singularity. One way to produce a L/4 singularity (the method used in ABAQUS) is to mesh L the region just near the crack tip with 8 noded elements, with a special arrangement of nodal points: (i) Three of the nodes (nodes 1,4 and 8 in the figure) are connected together, and (ii) the mid-side nodes 2 and 7 are moved to the quarter-point location on the element side. -

AC Fischer-Cripps
A.C. Fischer-Cripps Introduction to Contact Mechanics Series: Mechanical Engineering Series ▶ Includes a detailed description of indentation stress fields for both elastic and elastic-plastic contact ▶ Discusses practical methods of indentation testing ▶ Supported by the results of indentation experiments under controlled conditions Introduction to Contact Mechanics, Second Edition is a gentle introduction to the mechanics of solid bodies in contact for graduate students, post doctoral individuals, and the beginning researcher. This second edition maintains the introductory character of the first with a focus on materials science as distinct from straight solid mechanics theory. Every chapter has been 2nd ed. 2007, XXII, 226 p. updated to make the book easier to read and more informative. A new chapter on depth sensing indentation has been added, and the contents of the other chapters have been completely overhauled with added figures, formulae and explanations. Printed book Hardcover ▶ 159,99 € | £139.99 | $199.99 The author begins with an introduction to the mechanical properties of materials, ▶ *171,19 € (D) | 175,99 € (A) | CHF 189.00 general fracture mechanics and the fracture of brittle solids. This is followed by a detailed description of indentation stress fields for both elastic and elastic-plastic contact. The discussion then turns to the formation of Hertzian cone cracks in brittle materials, eBook subsurface damage in ductile materials, and the meaning of hardness. The author Available from your bookstore or concludes with an overview of practical methods of indentation. ▶ springer.com/shop MyCopy Printed eBook for just ▶ € | $ 24.99 ▶ springer.com/mycopy Order online at springer.com ▶ or for the Americas call (toll free) 1-800-SPRINGER ▶ or email us at: [email protected]. -

Fracture and Deformation of Soft Materials and Structures
Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2018 Fracture and deformation of soft am terials and structures Zhuo Ma Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Aerospace Engineering Commons, Engineering Mechanics Commons, Materials Science and Engineering Commons, and the Mechanics of Materials Commons Recommended Citation Ma, Zhuo, "Fracture and deformation of soft am terials and structures" (2018). Graduate Theses and Dissertations. 16852. https://lib.dr.iastate.edu/etd/16852 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Fracture and deformation of soft materials and structures by Zhuo Ma A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Engineering Mechanics Program of Study Committee: Wei Hong, Co-major Professor Ashraf Bastawros, Co-major Professor Pranav Shrotriya Liang Dong Liming Xiong The student author, whose presentation of the scholarship herein was approved by the program of study committee, is solely responsible for the content of this dissertation. The Graduate College will ensure this dissertation is globally accessible and will not permit alterations after a degree is conferred. Iowa State University Ames, Iowa 2018 Copyright © Zhuo Ma, 2018. All rights reserved. ii TABLE OF CONTENTS Page LIST OF FIGURES .......................................................................................................... -

Cross-Linked Polymers and Rubber Elasticity Chapter 9 (Sperling)
Cross-linked Polymers and Rubber Elasticity Chapter 9 (Sperling) • Definition of Rubber Elasticity and Requirements • Cross-links, Networks, Classes of Elastomers (sections 1-3, 16) • Simple Theory of Rubber Elasticity (sections 4-8) – Entropic Origin of Elastic Retractive Forces – The Ideal Rubber Behavior • Departures from the Ideal Rubber Behavior (sections 9-11) – Non-zero Energy Contribution to the Elastic Retractive Forces – Stress-induced Crystallization and Limited Extensibility of Chains (How to make better elastomers: High Strength and High Modulus) – Network Defects (dangling chains, loops, trapped entanglements, etc..) – Semi-empirical Mooney-Rivlin Treatment (Affine vs Non-Affine Deformation) Definition of Rubber Elasticity and Requirements • Definition of Rubber Elasticity: Very large deformability with complete recoverability. • Molecular Requirements: – Material must consist of polymer chains. Need to change conformation and extension under stress. – Polymer chains must be highly flexible. Need to access conformational changes (not w/ glassy, crystalline, stiff mat.) – Polymer chains must be joined in a network structure. Need to avoid irreversible chain slippage (permanent strain). One out of 100 monomers must connect two different chains. Connections (covalent bond, crystallite, glassy domain in block copolymer) Cross-links, Networks and Classes of Elastomers • Chemical Cross-linking Process: Sol-Gel or Percolation Transition • Gel Characteristics: – Infinite Viscosity – Non-zero Modulus – One giant Molecule – Solid -

Chapter 10: Elasticity and Oscillations
Chapter 10 Lecture Outline 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Chapter 10: Elasticity and Oscillations •Elastic Deformations •Hooke’s Law •Stress and Strain •Shear Deformations •Volume Deformations •Simple Harmonic Motion •The Pendulum •Damped Oscillations, Forced Oscillations, and Resonance 2 §10.1 Elastic Deformation of Solids A deformation is the change in size or shape of an object. An elastic object is one that returns to its original size and shape after contact forces have been removed. If the forces acting on the object are too large, the object can be permanently distorted. 3 §10.2 Hooke’s Law F F Apply a force to both ends of a long wire. These forces will stretch the wire from length L to L+L. 4 Define: L The fractional strain L change in length F Force per unit cross- stress A sectional area 5 Hooke’s Law (Fx) can be written in terms of stress and strain (stress strain). F L Y A L YA The spring constant k is now k L Y is called Young’s modulus and is a measure of an object’s stiffness. Hooke’s Law holds for an object to a point called the proportional limit. 6 Example (text problem 10.1): A steel beam is placed vertically in the basement of a building to keep the floor above from sagging. The load on the beam is 5.8104 N and the length of the beam is 2.5 m, and the cross-sectional area of the beam is 7.5103 m2. -

Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M
Fracture Mechanics Elastic Plastic Fracture Mechanics Elastic Plastic Fracture Mechanics Presented by Calvin M. Stewart, PhD MECH 5390-6390 Fall 2020 Outline • Introduction to Non-Linear Materials • J-Integral • Energy Approach • As a Contour Integral • HRR-Fields • COD • J Dominance Introduction to Non-Linear Materials Introduction to Non-Linear Materials • Thus far we have restricted our fractured solids to nominally elastic behavior. • However, structural materials often cannot be characterized via LEFM. Non-Linear Behavior of Materials • Two other material responses are that the engineer may encounter are Non-Linear Elastic and Elastic-Plastic Introduction to Non-Linear Materials • Loading Behavior of the two materials is identical but the unloading path for the elastic plastic material allows for non-unique stress- strain solutions. For Elastic-Plastic materials, a generic “Constitutive Model” specifies the relationship between stress and strain as follows n tot =+ Ramberg-Osgood 0 0 0 0 Reference (or Flow/Yield) Stress (MPa) Dimensionaless Constant (unitless) 0 Reference (or Flow/Yield) Strain (unitless) n Strain Hardening Exponent (unitless) Introduction to Non-Linear Materials • Ramberg-Osgood Constitutive Model n increasing Ramberg-Osgood −n K = 00 Strain Hardening Coefficient, K = 0 0 E n tot K,,,,0 n=+ E Usually available for a variety of materials 0 0 0 Introduction to Non-Linear Materials • Within the context of EPFM two general ways of trying to solve fracture problems can be identified: 1. A search for characterizing parameters (cf. K, G, R in LEFM). 2. Attempts to describe the elastic-plastic deformation field in detail, in order to find a criterion for local failure. -
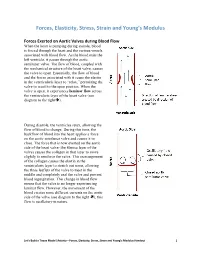
Forces, Elasticity, Stress, Strain and Young's Modulus Handout
Forces, Elasticity, Stress, Strain and Young’s Modulus Forces Exerted on Aortic Valves during Blood Flow When the heart is pumping during systole, blood is forced through the heart and the various vessels associated with blood flow. As the blood exits the left ventricle, it passes through the aortic semilunar valve. The flow of blood, coupled with the mechanical structure of the heart valve, causes the valve to open. Essentially, the flow of blood and the forces associated with it cause the elastin in the ventricularis layer to “relax,” permitting the valve to recoil to the open position. When the valve is open, it experiences laminar flow across the ventricularis layer of the heart valve (see diagram to the right). During diastole, the ventricles relax, allowing the flow of blood to change. During this time, the backflow of blood into the heart applies a force on the aortic semilunar valve and causes it to close. The force that is now exerted on the aortic side of the heart valve (the fibrosa layer of the valve) causes the collagen in that layer to move slightly to reinforce the valve. This rearrangement of the collagen causes the elastin in the ventricularis layer to stretch out some, allowing the three leaflets of the valve to meet in the middle and completely seal the valve and prevent blood regurgitation. This change in blood flow means that the valve is no longer experiencing laminar flow. However, the movement of the blood creates some different currents on the aortic side of the valve (see diagram to the right ); this flow is oscillatory in nature. -

Fracture Mechanics You Can Understand
Fracture Mechanics You Can Understand. John Goldak and Hossein Nimrouzi October 14, 2018 This document is intended to present much of the theory of linear elastic fracture mechanics (LEFM) in a way that is readily understandable to a second year engineering student. For a given crack geometry in a given structure, material type and boundary conditions, LEFM provides the formula below for the normal stress σyy(x; 0) on the crack plane with the crack. See Fig. 1. KI σyy(x; 0) = p f(θ) (1) 2πr p p where KI is the amplitude of the function f(θ)=( 2πr). The function f(θ)=( 2πr) is only a function of polar coordinates (r; θ). For a centre crack in an infinite plate with uniaxial ∗ tensile stress σyy before (without) the crack and crack length a, the value of the coefficient KI , which is called the stress intensity factor, is computed from the equation below. ∗ p KI = σyy πa (2) ∗ where σyy is is the traction normal to the crack plane evaluated in the UNCRACKED ∗ specimen or structure. Note that σyy and σyy(x; 0) are very different things. LEFM succeeded because experiments showed that if for a given material, crack geom- etry and load case, KI was less than a critical value called the fracture toughness that is denoted KIC , the crack was unlikely to grow rapidly and the risk the structure would fail was low. However, if KI was greater than the fracture toughness, the risk that the crack would grow rapidly and the structure would fail was high. -

SCK« CEN Stuimkchntrum VOOR Kl-.Rnfcnlrglt CTNTRF D'ftudl 1)1 I'fcnl-Rgil- MICI.FAIRF Precracking of Round Notched Bars
BE9800004 SCK« CEN STUIMKChNTRUM VOOR Kl-.RNfcNLRGlt CTNTRF D'FTUDl 1)1 I'fcNl-RGIl- MICI.FAIRF Precracking of round notched bars Progress Report M. Scibetta SCK-CEN Mol* Belgium Precracking of round notched bars Progress Report M. Scibetta SCK»CEN Mol, Belgium February, 1996 BLG-708 Precracking of round notched bars 1 Abstract 3 2 Introduction 3 3 Overview of precracking techniques 4 3.1 Introduction 4 3.2 Equipment 4 3.3 Eccentricity 5 3.4 Time required to precrack 5 3.5 Crack depth determination 5 3.5.1 The compliance method 6 3.5.1.1 Measuring force 6 3.5.1.2 Measuring displacement 6 3.5.1.3 Measuring an angle with a laser 6 3.5.1.4 Measuring force and displacement 7 3.5.2 Optical methods 7 3.5.3 The potential drop method 7 3.5.4 The resonance frequency method 8 3.6 Summary 8 4 Stress intensity factor and compliance of a bar under bending 9 4.1 Analytical expression 9 4.2 Stress intensity factor along the crack front 10 4.4 Combined effect of contact and eccentricity 12 4.5 Effect of mode II 12 4.6 Compliance 13 5 Stress intensity factor and compliance of a bar under bending using the finite element method (FEM) 15 5.1 Stress intensity factors 15 5.2 Compliance 17 6 Precracking system 18 6.2 Schematic representation of the experimental system 19 6.3 Initial stress intensity factor 19 6.4 Initial force 20 6.5 Initial contact pressure 20 6.6 Final force 22 6.7 Final stress intensity factor 22 7 Stress intensity factor of a precracked bar under tension 23 7.1 Analytical formulations 23 7.2 Finite element method 24 8 Compliance of a precracked bar under tension 26 8.1 Analytical formulations 26 8.2 Finite element method 27 9 Conclusions 28 10 Future investigations 29 11 References 30 Annex 1 Stress intensity factor and compliance function of a precracked bar under bending 33 Annex 2 Neutral axis position and stress intensity factor correction due to contact .34 Annex 3 Stress intensity factor and compliance function of a precracked bar under tension 35 1 Abstract Precracking round notched bars is the first step before fracture mechanics tests. -

Elasticity of Materials at High Pressure by Arianna Elizabeth Gleason A
Elasticity of Materials at High Pressure By Arianna Elizabeth Gleason A dissertation submitted in partial satisfaction of the Requirements for the degree of Doctor of Philosophy in Earth and Planetary Science in the GRADUATE DIVISION of the UNIVERSITY OF CALIFORNIA, BERKELEY Committee in charge: Professor Raymond Jeanloz, Chair Professor Hans-Rudolf Wenk Professor Kenneth Raymond Fall 2010 Elasticity of Materials at High Pressure Copyright 2010 by Arianna Elizabeth Gleason 1 Abstract Elasticity of Materials at High Pressure by Arianna Elizabeth Gleason Doctor of Philosophy in Earth and Planetary Science University of California, Berkeley Professor Raymond Jeanloz, Chair The high-pressure behavior of the elastic properties of materials is important for condensed matter and materials physics, and planetary and geosciences, as it contributes to the mechanical deformations and stability of solids under external stresses. The high-pressure elasticity of relevant minerals is of substantial geophysical importance for the Earth’s interior since they relate to (1) velocities of seismic waves and (2) the change in density that occurs when minerals are under pressure. Absence of samples from the deep interior prompts comparisons between seismological observations and the elastic properties of candidate minerals as a way to extract information regarding the composition and mineralogy of the Earth. Implementing a new method for measuring compressional- and shear-wave velocities, Vp and Vs, based on Brillouin spectroscopy of polycrystalline materials at high pressures, I examine four case studies: 1) soda-lime glass, 2) NaCl, 3) MgO, and 4) Kilauea basalt glass. The results on multigrain soda-lime glass show that even with an index differing by 3 percent, an oil medium removes the effects of multiple scattering from the Brillouin spectra of the glass powders; similarly, high-pressure Brillouin spectra from transparent polycrystalline samples should, in many cases, be free from optical-scattering effects.