A Distributed Heat Pulse Sensor Network for Thermo‐Hydraulic Monitoring Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
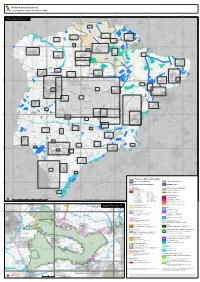
Rutland Main Map A0 Portrait
Rutland County Council Local Plan Pre-Submission Policies Map 480000 485000 490000 495000 500000 505000 Rutland County - Main map Thistleton Inset 53 Stretton (west) Clipsham Inset 51 Market Overton Inset 13 Inset 35 Teigh Inset 52 Stretton Inset 50 Barrow Greetham Inset 4 Inset 25 Cottesmore (north) 315000 Whissendine Inset 15 Inset 61 Greetham (east) Inset 26 Ashwell Cottesmore Inset 1 Inset 14 Pickworth Inset 40 Essendine Inset 20 Cottesmore (south) Inset 16 Ashwell (south) Langham Inset 2 Ryhall Exton Inset 30 Inset 45 Burley Inset 21 Inset 11 Oakham & Barleythorpe Belmesthorpe Inset 38 Little Casterton Inset 6 Rutland Water Inset 31 Inset 44 310000 Tickencote Great Inset 55 Casterton Oakham town centre & Toll Bar Inset 39 Empingham Inset 24 Whitwell Stamford North (Quarry Farm) Inset 19 Inset 62 Inset 48 Egleton Hambleton Ketton Inset 18 Inset 27 Inset 28 Braunston-in-Rutland Inset 9 Tinwell Inset 56 Brooke Inset 10 Edith Weston Inset 17 Ketton (central) Inset 29 305000 Manton Inset 34 Lyndon Inset 33 St. George's Garden Community Inset 64 North Luffenham Wing Inset 37 Inset 63 Pilton Ridlington Preston Inset 41 Inset 43 Inset 42 South Luffenham Inset 47 Belton-in-Rutland Inset 7 Ayston Inset 3 Morcott Wardley Uppingham Glaston Inset 36 Tixover Inset 60 Inset 58 Inset 23 Barrowden Inset 57 Inset 5 Uppingham town centre Inset 59 300000 Bisbrooke Inset 8 Seaton Inset 46 Eyebrook Reservoir Inset 22 Lyddington Inset 32 Stoke Dry Inset 49 Thorpe by Water Inset 54 Key to Policies on Main and Inset Maps Rutland County Boundary Adjoining -

BRONZE AGE SETTLEMENT at RIDLINGTON, RUTLAND Matthew Beamish
01 Ridlington - Beamish 30/9/05 3:19 pm Page 1 BRONZE AGE SETTLEMENT AT RIDLINGTON, RUTLAND Matthew Beamish with contributions from Lynden Cooper, Alan Hogg, Patrick Marsden, and Angela Monckton A post-ring roundhouse and adjacent structure were recorded by University of Leicester Archaeological Services, during archaeological recording preceding laying of the Wing to Whatborough Hill trunk main in 1996 by Anglian Water plc. The form of the roundhouse together with the radiocarbon dating of charred grains and finds of pottery and flint indicate that the remains stemmed from occupation toward the end of the second millennium B.C. The distribution of charred cereal remains within the postholes indicates that grain including barley was processed and stored on site. A pit containing a small quantity of Beaker style pottery was also recorded to the east, whilst a palaeolith was recovered from the infill of a cryogenic fissure. The remains were discovered on the northern edge of a flat plateau of Northamptonshire Sand Ironstone at between 176 and 177m ODSK832023). The plateau forms a widening of a west–east ridge, a natural route way, above northern slopes down into the Chater Valley, and abrupt escarpments above the parishes of Ayston and Belton to the south (illus. 2). Near to the site, springs issue from just below the 160m and 130m contours to the north and south east respectively and ponds exist to the east corresponding with a boulder clay cap. The area was targeted for investigation as it lay on the northern fringe of a substantial Mesolithic/Early Neolithic flint scatter (LE5661, 5662, 5663) (illus. -

Designated Rural Areas and Designated Regions) (England) Order 2004
Status: This is the original version (as it was originally made). This item of legislation is currently only available in its original format. STATUTORY INSTRUMENTS 2004 No. 418 HOUSING, ENGLAND The Housing (Right to Buy) (Designated Rural Areas and Designated Regions) (England) Order 2004 Made - - - - 20th February 2004 Laid before Parliament 25th February 2004 Coming into force - - 17th March 2004 The First Secretary of State, in exercise of the powers conferred upon him by sections 157(1)(c) and 3(a) of the Housing Act 1985(1) hereby makes the following Order: Citation, commencement and interpretation 1.—(1) This Order may be cited as the Housing (Right to Buy) (Designated Rural Areas and Designated Regions) (England) Order 2004 and shall come into force on 17th March 2004. (2) In this Order “the Act” means the Housing Act 1985. Designated rural areas 2. The areas specified in the Schedule are designated as rural areas for the purposes of section 157 of the Act. Designated regions 3.—(1) In relation to a dwelling-house which is situated in a rural area designated by article 2 and listed in Part 1 of the Schedule, the designated region for the purposes of section 157(3) of the Act shall be the district of Forest of Dean. (2) In relation to a dwelling-house which is situated in a rural area designated by article 2 and listed in Part 2 of the Schedule, the designated region for the purposes of section 157(3) of the Act shall be the district of Rochford. (1) 1985 c. -

Royal Forest Trail
Once there was a large forest on the borders of Rutland called the Royal Forest of Leighfield. Now only traces remain, like Prior’s Coppice, near Leighfield Lodge. The plentiful hedgerows and small fields in the area also give hints about the past vegetation cover. Villages, like Belton and Braunston, once deeply situated in the forest, are square shaped. This is considered to be due to their origin as enclosures within the forest where the first houses surrounded an open space into which animals could be driven for their protection and greater security - rather like the covered wagon circle in the American West. This eventually produced a ‘hollow-centred’ village later filled in by buildings. In Braunston the process of filling in the centre had been going on for many centuries. Ridlington betrays its forest proximity by its ‘dead-end’ road, continued only by farm tracks today. The forest blocked entry in this direction. Indeed, if you look at the 2 ½ inch O.S map you will notice that there are no through roads between Belton and Braunston due to the forest acting as a physical administrative barrier. To find out more about this area, follow this trail… You can start in Oakham, going west out of town on the Cold Overton Road, then 2nd left onto West Road towards Braunston. Going up the hill to Braunston. In Braunston, walk around to see the old buildings such as Cheseldyn Farm and Quaintree Hall; go down to the charming little bridge over the River Gwash (the stream flowing into Rutland Water). -

Local Plan Review Issues and Options Consultation Document
1 Rutland Local Plan Review Issues and Options Consultation Contents Introduction ......................................................................................................................... 3 How can sites for new housing and other development be put forward? ........................... 6 Neighbourhood Plans............................................................................................................ 8 What role should the Local Plan take in coordinating neighbourhood plans? .................... 8 The spatial portrait, vision and objectives .............................................................................. 9 Are changes to the spatial portrait, vision or objectives needed? ...................................... 9 The spatial strategy ............................................................................................................. 10 Are changes to the settlement hierarchy needed? ........................................................... 10 How much new housing will be needed? ......................................................................... 16 Will sites for employment, retail or other uses need to be allocated?............................... 18 What type of new housing is going to be needed? .......................................................... 19 How will new development be apportioned between the towns and villages? .................. 21 How will new growth be apportioned between Oakham and Uppingham? ....................... 23 Site allocations ................................................................................................................... -

Areas Designated As 'Rural' for Right to Buy Purposes
Areas designated as 'Rural' for right to buy purposes Region District Designated areas Date designated East Rutland the parishes of Ashwell, Ayston, Barleythorpe, Barrow, 17 March Midlands Barrowden, Beaumont Chase, Belton, Bisbrooke, Braunston, 2004 Brooke, Burley, Caldecott, Clipsham, Cottesmore, Edith SI 2004/418 Weston, Egleton, Empingham, Essendine, Exton, Glaston, Great Casterton, Greetham, Gunthorpe, Hambelton, Horn, Ketton, Langham, Leighfield, Little Casterton, Lyddington, Lyndon, Manton, Market Overton, Martinsthorpe, Morcott, Normanton, North Luffenham, Pickworth, Pilton, Preston, Ridlington, Ryhall, Seaton, South Luffenham, Stoke Dry, Stretton, Teigh, Thistleton, Thorpe by Water, Tickencote, Tinwell, Tixover, Wardley, Whissendine, Whitwell, Wing. East of North Norfolk the whole district, with the exception of the parishes of 15 February England Cromer, Fakenham, Holt, North Walsham and Sheringham 1982 SI 1982/21 East of Kings Lynn and the parishes of Anmer, Bagthorpe with Barmer, Barton 17 March England West Norfolk Bendish, Barwick, Bawsey, Bircham, Boughton, Brancaster, 2004 Burnham Market, Burnham Norton, Burnham Overy, SI 2004/418 Burnham Thorpe, Castle Acre, Castle Rising, Choseley, Clenchwarton, Congham, Crimplesham, Denver, Docking, Downham West, East Rudham, East Walton, East Winch, Emneth, Feltwell, Fincham, Flitcham cum Appleton, Fordham, Fring, Gayton, Great Massingham, Grimston, Harpley, Hilgay, Hillington, Hockwold-Cum-Wilton, Holme- Next-The-Sea, Houghton, Ingoldisthorpe, Leziate, Little Massingham, Marham, Marshland -

English Hundred-Names
l LUNDS UNIVERSITETS ARSSKRIFT. N. F. Avd. 1. Bd 30. Nr 1. ,~ ,j .11 . i ~ .l i THE jl; ENGLISH HUNDRED-NAMES BY oL 0 f S. AND ER SON , LUND PHINTED BY HAKAN DHLSSON I 934 The English Hundred-Names xvn It does not fall within the scope of the present study to enter on the details of the theories advanced; there are points that are still controversial, and some aspects of the question may repay further study. It is hoped that the etymological investigation of the hundred-names undertaken in the following pages will, Introduction. when completed, furnish a starting-point for the discussion of some of the problems connected with the origin of the hundred. 1. Scope and Aim. Terminology Discussed. The following chapters will be devoted to the discussion of some The local divisions known as hundreds though now practi aspects of the system as actually in existence, which have some cally obsolete played an important part in judicial administration bearing on the questions discussed in the etymological part, and in the Middle Ages. The hundredal system as a wbole is first to some general remarks on hundred-names and the like as shown in detail in Domesday - with the exception of some embodied in the material now collected. counties and smaller areas -- but is known to have existed about THE HUNDRED. a hundred and fifty years earlier. The hundred is mentioned in the laws of Edmund (940-6),' but no earlier evidence for its The hundred, it is generally admitted, is in theory at least a existence has been found. -

Uppingham Parish Plan
UPPINGHAM PARISH PLAN OCTOBER 2007 UPPINGHAM PARISH PLAN Introduction In April 2006 a steering group was formed with the support of the Rural Community Council and Uppingham Town Council to prepare a plan for the future of Uppingham. We are grateful to the staff of both Councils for their help and encouragement. The group prepared a questionnaire that was delivered to all households in the town early in 2007. The responses to this questionnaire were analysed and it is relevant that more than 50% of respondents described themselves as retired. The views of the respondents form the plan and it is clear that they like their town and are concerned about changes taking place without consultation. However they accept that if changes must take place such changes take into account their views and the character and history of the town. The plan is to be taken into account by the Town Council, Rutland County Council, National Government and statutory service providers in matters affecting Uppingham. The group has considered it important to provide a background to the plan by reference to history and the town at the present time. We believe all facts to be correct and apologise if there are any errors or omissions. Neil Hermsen – Chairman of the Steering Group A little local history Although Uppingham does not appear in the Domesday Book there is little doubt that a set- tlement existed for many years before the Norman Conquest. The name, deriving from the “Ham of the Yppingas” meaning “people of the upland”, indicates that it came into existence by the early 6th century but the settlement may have come into being even earlier. -

Profession-Led HLP Level 1 Register - East Midlands 23/11/2017
Profession-Led HLP Level 1 Register - East Midlands 23/11/2017 GPHC Pharmacy Name Number Street Address City County Postcode Telephone 3 Queen 3q Pharmacy 1105385 Street Wellingborough Northamptonshire NN8 4RW 01933273373 84b Berners 7-11 Pharmacy 1100687 Street Leicester Leicestershire LE2 0FS 01162511333 Abbey 63 Central Pharmacy 1096941 Avenue Nottingham Nottinghamshire NG9 2QP 01159254522 Acorn 8-10 Main Pharmacy 1035692 Road Jacksdale Nottinghamshire NG16 5JW 01773602759 Alan Stockley Pharmacy 1035279 37 Lynn Road Snettisham Norfolk PE31 7LR 01485541230 224 Alpharm Loghborough Chemist 1034092 Road Leicester Leicestershire LE4 5LG 01162661604 224 Alpharm Loughborough Chemist Ltd 1034092 Road Leicester Leicestershire LE45LG 01162661604 Main Street, Amber Horsley Pharmacy 1092960 Woodhouse Ilkeston Derbyshire DE76AX 01332782844 Applegate Pharmacy 1035596 132 Alfreton Rd Nottingham Nottinghamshire NG73NS 01159785744 Arley Rowlands Pharmacy 1116812 Court Arley Warwickshire CV78PF 01676549195 ASDA Pharmacy 111-127 Front Arnold 1113527 Street Arnold Nottingham NG5 7ED 01159649110 Asda Pharmacy Bletcham Way 1090788 Bletcham Way Milton Keynes Buckinghamshire MK1 1QB 01908362510 Profession-Led HLP Level 1 Register - East Midlands 23/11/2017 Asda Pharmacy Derby Road, Derby Road, Spondon 1030344 Spondon Derby Derbyshire DE21 7UY 01332826719 Asda Pharmacy Hinckley 1034003 Barwell Lane Hinckley Leics LE5 5TL 01455896719 Asda Pharmacy Hyson Green 1035714 Radford Road Hyson Green Nottingham NG7 5FP 01159002510 Narborough Asda Road South, Pharmacy -

2004 No. 418 HOUSING, ENGLAND the Housing
STATUTORY INSTRUMENTS 2004 No. 418 HOUSING, ENGLAND The Housing (Right to Buy) (Designated Rural Areas and Designated Regions) (England) Order 2004 Made - - - - 20th February 2004 Laid before Parliament 25th February 2004 Coming into force - - 17th March 2004 The First Secretary of State, in exercise of the powers conferred upon him by sections 157(1)(c) and 3(a) of the Housing Act 1985(a) hereby makes the following Order: Citation, commencement and interpretation 1.—(1) This Order may be cited as the Housing (Right to Buy) (Designated Rural Areas and Designated Regions) (England) Order 2004 and shall come into force on 17th March 2004. (2) In this Order “the Act” means the Housing Act 1985. Designated rural areas 2. The areas specified in the Schedule are designated as rural areas for the purposes of section 157 of the Act. Designated regions 3.—(1) In relation to a dwelling-house which is situated in a rural area designated by article 2 and listed in Part 1 of the Schedule, the designated region for the purposes of section 157(3) of the Act shall be the district of Forest of Dean. (2) In relation to a dwelling-house which is situated in a rural area designated by article 2 and listed in Part 2 of the Schedule, the designated region for the purposes of section 157(3) of the Act shall be the district of Rochford. (3) In relation to a dwelling-house which is situated in a rural area designated by article 2 and listed in Part 3 of the Schedule, the designated region for the purposes of section 157(3) of the Act shall be the district of Rutland. -
Out of Print Click to Download
Number One . .. " .. "'. '\� . .. :,;. :':f..• � .,1- '. , ... .Alt,;'�: ' � .. :: ",' , " • .r1� .: : •.: . .... .' , "" "" "·';'i:\:.'·'�., ' ' • •• ·.1 ..:',.. , ..... ,:.' ::.,::: ; ')"'� ,\:.", . '." � ' ,., d',,,·· '� . ' . � ., ., , , " ,' . ":'�, , " ,I -; .. ',' :... .: . :. , . : . ,',." The Rutland Record Society was formed in May 1979. Its object is to advise the education of the public in the history of the Ancient County of Rutland, in particular by collecting, preserving, printing and publishing historical records relating to that County, making such records accessible for research purposes to anyone following a particular line of historical study, and stimUlating interest generally in the history of that County. PATRON Col. T.C.S. Haywood, O.B.E., J.P. H.M. Lieutenant for the County of Leicestershire with special responsibility for Rutland PRESIDENT G.H. Boyle, Esq., Bisbrooke Hall, Uppingham CHAIRMAN Prince Yuri Galitzine, Quaintree Hall, Braunston, Oakham VICE-CHAIRMAN Miss J. Spencer, The Orchard, Braunston, Oakham HONORARY SECRETARIES B. Matthews, Esq., Colley Hill, Lyddington, Uppingham M.E. Baines, Esq., 14 Main Street, Ridlington, Uppingham HONORAR Y TREASURER The Manager, Midland Bank Limited, 28 High Street, Oakham HONORARY SOLICITOR J.B. Ervin, Esq., McKinnell, Ervin & MitchelI, 1 & 3 New Street, Leicester HONORARY ARCHIVIST G.A. Chinnery, Esq., Pear Tree Cottage, Hungarton, Leicestershire HONORAR Y EDITOR Bryan Waites, Esq., 6 Chater Road, Oakham COUNCIL President, Chairman, Vice-Chairman, Trustees, Secretaries, -

Polling Station Postal Address
Polling place addresses Parishes voting at station Ridlington Village Hall Ayston Main Street Ridlington Ridlington Oakham Rutland LE15 9AU Belton Village Hall Belton-in-Rutland Main Street Belton-in-Rutland LE15 9LB Braunston Village Hall Braunston-in-Rutland Wood Lane Brooke Braunston-in-Rutland Leighfield Oakham Rutland LE15 8QZ Preston Village Hall Preston Main Street Preston Oakham Rutland LE15 9NJ Cottesmore Village Hall The Community Centre Barrow 23 Main Street Cottesmore Cottesmore Oakham Rutland LE15 7DH Market Overton Village Hall Market Overton 52 Main Street Market Overton Oakham Rutland LE15 7PL Ashwell Village Hall Ashwell Brookdene Burley Ashwell Oakahm Rutland LE15 7LQ Egleton Village Hall Egleton Church Lane Hambleton Oakham Rutland LE15 8AD Exton Village Hall Exton & Horn The Green Whitwell Exton Oakham Rutland LE15 8AP The Olive Branch, Clipsham Clipsham Pickworth Main Street Clipsham Oakham Rutland LE15 7SH Greetham Community Centre Greetham Great Lane Greetham Oakham Rutland LE15 7NG Jackson Stops, Stretton Stretton Rookery Lane Thistleton Stretton Oakham Rutland LE15 7RA Barrowden Village Hall Barrowden Wakerley Road Barrowden Oakham Rutland LE15 8EP Ketton Library Ketton High Street Tixover Ketton Stamford Lincs PE9 3TE Tinwell Village Hall Tinwell Rear of All Saints Church Off Crown Lane Tinwell Nr Stamford Lincs PE9 3UD Langham Village Hall Langham Church Street Langham Oakham Rutland LE15 7HY St John The Baptist Church Bisbrooke Church Lane Bisbrooke Uppingham LE15 9EL Caldecott Village Hall Caldecott Church