DOCSLIB.ORG

Identify Equations, Point of Intersection of Equations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Identify Equations, Point of Intersection of Equations Chapter 8 Systems: Identify Equations, Point of Intersection of Equations Classification of Second Degree Equations When you write a conic section in its general form, you have an equation of the form Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 . (All of the equations we have seen so far have a value for B that is 0.) With only minimal work, you can determine if an equation in this form is a circle, an ellipse, a parabola or a hyperbola. If A, B and C are not all 0, and if the graph if not degenerate (point, line or two lines), then: • The graph is a circle if B 2 − 4AC < 0 and A = C . • The graph is an ellipse if B 2 − 4AC < 0 and A ≠ C . • The graph is a parabola if B 2 − 4AC = 0 . • The graph is a hyperbola if B 2 − 4AC > 0 . Remember, if there is no “xy” term, then B = 0. Recall the following equations: Parabola: (yk− )4(2 = pxh − ) or (xh− )4(2 = pyk − ) . Circle: (x − h)2 + (y − k)2 = r 2 (xh− )(2 yk − ) 2 Ellipse: + = 1 number number (xh− )(2 yk − ) 2 (yk− )(2 xh − ) 2 Hyperbola: − = 1 or − = 1 a2 b 2 a2 b 2 Example 1: Identify each conic. (Note, none of these are degenerates conics.) (x − 2)2 (y + 2)2 a. 12 x = y 2 b. − = 1 9 16 (x + 4)2 (y −1)2 c. + = 1 d. 6x 2 − 4xy + 3y 2 + 5x − 7y + 3 = 0 4 9 Chapter 8 – Systems 1 e. 2x 2 − 8y 2 − 6x −16 y − 25 = 0 Sometimes equations that look like they should be conic sections do not behave very well. For example, I. (x − 3)2 + (y +1)2 = 0 represents a point (3, -1). Looks like it could be a circle equation, but r = 0. II. 9x 2 − 4y 2 = 0 represents 2 lines. Looks like it could be a hyperbola, but right hand- side is 0, not 1. Solve for y: 4y 2 = 9x 2 9x 2 y 2 = 4 3x y = ± 2 III. 2x 2 + 3y 2 = −1 represents nothing, no graph, no point, no line(s). Looks like it could be an ellipse, but right hand-side is -1, not 1. These are all examples of degenerate conic sections . You will not see these very often, but you should be aware of them. Chapter 8 – Systems 2 Systems of Second Degree Equations When we graph two conic sections or a conic section and a line on the same coordinate planes, their graphs may contain points of intersection. The graph below shows a hyperbola and a line and contains two points of intersection. We want to be able to find the points of intersection. To do this, we will solve a system of equations, but now one or both of the equations will be second degree equations. Determining the points of intersection graphically is difficult, so we will do these algebraically. Example 2: Solve the system of equations: f (x) = −2x 2 + 8x − 5 g(x) = 6x − 5 Chapter 8 – Systems 3 Example 3: Solve the system of equations: x 2 + y 2 = 4 4x 2 − y 2 = 1 Example 4: Solve the system of equations: (x − )1 2 + (y − )3 2 = 4 y = x Chapter 8 – Systems 4 Example 5: Graph each equation and determine the number of points of intersection of the two graphs. x 2 + y 2 = 64 x 2 y 2 + = 1 25 9 5 y 4 3 2 1 x −9 −8 −7 −6 −5 −4 −3 −2 −1 1 2 3 4 5 6 7 8 9 −1 −2 −3 −4 −5 Chapter 8 – Systems 5 Review Test 4 MATH 1330 Review for Test -4 Time: 50 minutes Number of questions: ~7 Multiple Choice ~3 Free Response What is covered: Chapters 7 and 8. Do not forget to reserve a seat for Test – 4! Take practice Test – 4! Example 1: A ramp for wheelchair accessibility is to be constructed with an angle of elevation of 14 degrees and a final height of 4 ft. How long is the ramp? Example 2: Find the area of triangle XYZ if ∠Y = 60° , z = 8 and x = 4. Example 3: ABC is a triangle with AB = 10, BC = 13, and AC = 7. Find cos(A). Note: You are asked to find cos(A) not the measure of angle A. Do not use a calculator. Review Test 4 Example 4: Given triangle ABC with AB = 3, and BC = 3√2 The measure of angle A is 135o. How many choices are there for the measure of angle C? Example 5: In acute triangle ABC, the measure of angle A is 2x, the length of AB is 7, and the length of AC is √3. If sin(x) = 1∕6 , what is the area of the triangle? Example 6: Two cyclists leave the corner of State Street and Main Street simultaneously. State Street and Main Street are not at right angles; the cyclists' paths have an angle of 150o between them. How far apart are the cyclists after they each travel 7 miles? Review Test 4 Example 7: ABC is a triangle with AB = 9, BC = 14, and AC = 12. Find cos(A). Note: You are asked to find cos(A) not the measure of angle A. Do not use a calculator. Example 8: Find the coordinates of the center and the radius for the given circle. 12 830 Review Test 4 Example 9: Given the following, find: 1 144 25 a. The vertices b. The foci c. Equations of the asymptotes Example 10: Graph 16 Vertex Focal Point End points of the focal chord .
Load more

Recommended publications
  • Proofs with Perpendicular Lines
    3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units.
    [Show full text]
  • Some Intersection Theorems for Ordered Sets and Graphs
    IOURNAL OF COMBINATORIAL THEORY, Series A 43, 23-37 (1986) Some Intersection Theorems for Ordered Sets and Graphs F. R. K. CHUNG* AND R. L. GRAHAM AT&T Bell Laboratories, Murray Hill, New Jersey 07974 and *Bell Communications Research, Morristown, New Jersey P. FRANKL C.N.R.S., Paris, France AND J. B. SHEARER' Universify of California, Berkeley, California Communicated by the Managing Editors Received May 22, 1984 A classical topic in combinatorics is the study of problems of the following type: What are the maximum families F of subsets of a finite set with the property that the intersection of any two sets in the family satisfies some specified condition? Typical restrictions on the intersections F n F of any F and F’ in F are: (i) FnF’# 0, where all FEF have k elements (Erdos, Ko, and Rado (1961)). (ii) IFn F’I > j (Katona (1964)). In this paper, we consider the following general question: For a given family B of subsets of [n] = { 1, 2,..., n}, what is the largest family F of subsets of [n] satsifying F,F’EF-FnFzB for some BE B. Of particular interest are those B for which the maximum families consist of so- called “kernel systems,” i.e., the family of all supersets of some fixed set in B. For example, we show that the set of all (cyclic) translates of a block of consecutive integers in [n] is such a family. It turns out rather unexpectedly that many of the results we obtain here depend strongly on properties of the well-known entropy function (from information theory).
    [Show full text]
  • Complete Intersection Dimension
    PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. LUCHEZAR L. AVRAMOV VESSELIN N. GASHAROV IRENA V. PEEVA Complete intersection dimension Publications mathématiques de l’I.H.É.S., tome 86 (1997), p. 67-114 <http://www.numdam.org/item?id=PMIHES_1997__86__67_0> © Publications mathématiques de l’I.H.É.S., 1997, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http:// www.ihes.fr/IHES/Publications/Publications.html) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou im- pression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ COMPLETE INTERSECTION DIMENSION by LUGHEZAR L. AVRAMOV, VESSELIN N. GASHAROV, and IRENA V. PEEVA (1) Abstract. A new homological invariant is introduced for a finite module over a commutative noetherian ring: its CI-dimension. In the local case, sharp quantitative and structural data are obtained for modules of finite CI- dimension, providing the first class of modules of (possibly) infinite projective dimension with a rich structure theory of free resolutions. CONTENTS Introduction ................................................................................ 67 1. Homological dimensions ................................................................... 70 2. Quantum regular sequences ..............................................................
    [Show full text]
  • And Are Lines on Sphere B That Contain Point Q
    11-5 Spherical Geometry Name each of the following on sphere B. 3. a triangle SOLUTION: are examples of triangles on sphere B. 1. two lines containing point Q SOLUTION: and are lines on sphere B that contain point Q. ANSWER: 4. two segments on the same great circle SOLUTION: are segments on the same great circle. ANSWER: and 2. a segment containing point L SOLUTION: is a segment on sphere B that contains point L. ANSWER: SPORTS Determine whether figure X on each of the spheres shown is a line in spherical geometry. 5. Refer to the image on Page 829. SOLUTION: Notice that figure X does not go through the pole of ANSWER: the sphere. Therefore, figure X is not a great circle and so not a line in spherical geometry. ANSWER: no eSolutions Manual - Powered by Cognero Page 1 11-5 Spherical Geometry 6. Refer to the image on Page 829. 8. Perpendicular lines intersect at one point. SOLUTION: SOLUTION: Notice that the figure X passes through the center of Perpendicular great circles intersect at two points. the ball and is a great circle, so it is a line in spherical geometry. ANSWER: yes ANSWER: PERSEVERANC Determine whether the Perpendicular great circles intersect at two points. following postulate or property of plane Euclidean geometry has a corresponding Name two lines containing point M, a segment statement in spherical geometry. If so, write the containing point S, and a triangle in each of the corresponding statement. If not, explain your following spheres. reasoning. 7. The points on any line or line segment can be put into one-to-one correspondence with real numbers.
    [Show full text]
  • Device Constructions with Hyperbolas
    Device Constructions with Hyperbolas Alfonso Croeze1 William Kelly1 William Smith2 1Department of Mathematics Louisiana State University Baton Rouge, LA 2Department of Mathematics University of Mississippi Oxford, MS July 8, 2011 Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Two Foci Focus and Directrix Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas The Project Basic constructions Constructing a Hyperbola Advanced constructions Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Rusty Compass Theorem Given a circle centered at a point A with radius r and any point C different from A, it is possible to construct a circle centered at C that is congruent to the circle centered at A with a compass and straightedge. Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X D B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas A B X Y Angle Duplication A X Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Angle Duplication A X A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Constructing a Perpendicular C C A B Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C C X X O A B A B Y Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas We needed a way to draw a hyperbola.
    [Show full text]
  • Intersection of Convex Objects in Two and Three Dimensions
    Intersection of Convex Objects in Two and Three Dimensions B. CHAZELLE Yale University, New Haven, Connecticut AND D. P. DOBKIN Princeton University, Princeton, New Jersey Abstract. One of the basic geometric operations involves determining whether a pair of convex objects intersect. This problem is well understood in a model of computation in which the objects are given as input and their intersection is returned as output. For many applications, however, it may be assumed that the objects already exist within the computer and that the only output desired is a single piece of data giving a common point if the objects intersect or reporting no intersection if they are disjoint. For this problem, none of the previous lower bounds are valid and algorithms are proposed requiring sublinear time for their solution in two and three dimensions. Categories and Subject Descriptors: E.l [Data]: Data Structures; F.2.2 [Analysis of Algorithms]: Nonnumerical Algorithms and Problems General Terms: Algorithms, Theory, Verification Additional Key Words and Phrases: Convex sets, Fibonacci search, Intersection 1. Introduction This paper describes fast algorithms for testing the predicate, Do convex objects P and Q intersect? where an object is taken to be a line or a polygon in two dimensions or a plane or a polyhedron in three dimensions. The related problem Given convex objects P and Q, compute their intersection has been well studied, resulting in linear lower bounds and linear or quasi-linear upper bounds [2, 4, 11, 15-171. Lower bounds for this problem use arguments This research was supported in part by the National Science Foundation under grants MCS 79-03428, MCS 81-14207, MCS 83-03925, and MCS 83-03926, and by the Defense Advanced Project Agency under contract F33615-78-C-1551, monitored by the Air Force Offtce of Scientific Research.
    [Show full text]
  • Section 6.2 Introduction to Conics: Parabolas 103
    Section 6.2 Introduction to Conics: Parabolas 103 Course Number Section 6.2 Introduction to Conics: Parabolas Instructor Objective: In this lesson you learned how to write the standard form of the equation of a parabola. Date Important Vocabulary Define each term or concept. Directrix A fixed line in the plane from which each point on a parabola is the same distance as the distance from the point to a fixed point in the plane. Focus A fixed point in the plane from which each point on a parabola is the same distance as the distance from the point to a fixed line in the plane. Focal chord A line segment that passes through the focus of a parabola and has endpoints on the parabola. Latus rectum The specific focal chord perpendicular to the axis of a parabola. Tangent A line is tangent to a parabola at a point on the parabola if the line intersects, but does not cross, the parabola at the point. I. Conics (Page 433) What you should learn How to recognize a conic A conic section, or conic, is . the intersection of a plane as the intersection of a and a double-napped cone. plane and a double- napped cone Name the four basic conic sections: circle, ellipse, parabola, and hyperbola. In the formation of the four basic conics, the intersecting plane does not pass through the vertex of the cone. When the plane does pass through the vertex, the resulting figure is a(n) degenerate conic , such as . a point, a line, or a pair of intersecting lines.
    [Show full text]
  • Apollonius of Pergaconics. Books One - Seven
    APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro].
    [Show full text]
  • Stable Rationality of Quadric Surface Bundles Over Surfaces
    STABLE RATIONALITY OF QUADRIC SURFACE BUNDLES OVER SURFACES BRENDAN HASSETT, ALENA PIRUTKA, AND YURI TSCHINKEL Abstract. We study rationality properties of quadric surface bun- dles over the projective plane. We exhibit families of smooth pro- jective complex fourfolds of this type over connected bases, con- taining both rational and non-rational fibers. 1. Introduction Is a deformation of a smooth rational (or irrational) projective vari- ety still rational (or irrational)? The main goal of this paper is to show that rationality is not deformation invariant for families of smooth com- plex projective varieties of dimension four. Examples along these lines are known when singular fibers are allowed, e.g., smooth cubic three- folds (which are irrational) may specialize to cubic threefolds with or- dinary double points (which are rational), while smooth cubic surfaces (which are rational) may specialize to cones over elliptic curves. Totaro shows that specializations of rational varieties need not be rational in higher dimensions if mild singularities are allowed [Tot16b]. However, de Fernex and Fusi [dFF13] show that the locus of rational fibers in a smooth family of projective complex threefolds is a countable union of closed subsets on the base. Let S be a smooth projective rational surface over the complex num- bers with function field K = C(S). A quadric surface bundle consists of a fourfold X and a flat projective morphism π : X ! S such that the generic fiber Q=K of π is a smooth quadric surface. We assume that π factors through the projectivization of a rank four vector bundle on S such that the fibers are (possibly singular) quadric surfaces; see Section 3 for relevant background.
    [Show full text]
  • 14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler
    14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler Preliminaries: Conic Sections Ellipses, parabolas and hyperbolas can all be generated by cutting a cone with a plane (see diagrams, from Wikimedia Commons). Taking the cone to be xyz222+=, and substituting the z in that equation from the planar equation rp⋅= p, where p is the vector perpendicular to the plane from the origin to the plane, gives a quadratic equation in xy,. This translates into a quadratic equation in the plane—take the line of intersection of the cutting plane with the xy, plane as the y axis in both, then one is related to the other by a scaling xx′ = λ . To identify the conic, diagonalized the form, and look at the coefficients of xy22,. If they are the same sign, it is an ellipse, opposite, a hyperbola. The parabola is the exceptional case where one is zero, the other equates to a linear term. It is instructive to see how an important property of the ellipse follows immediately from this construction. The slanting plane in the figure cuts the cone in an ellipse. Two spheres inside the cone, having circles of contact with the cone CC, ′, are adjusted in size so that they both just touch the plane, at points FF, ′ respectively. It is easy to see that such spheres exist, for example start with a tiny sphere inside the cone near the point, and gradually inflate it, keeping it spherical and touching the cone, until it touches the plane. Now consider a point P on the ellipse.
    [Show full text]
  • 2.3 Conic Sections: Hyperbola ( ) ( ) ( )
    2.3 Conic Sections: Hyperbola Hyperbola (locus definition) Set of all points (x, y) in the place such that the absolute value of the difference of each distances from F1 and F2 to (x, y) is a constant distance, d. In the figure above: The distance from F1 to (x1, y1 ) - the distance from F2 to (x1, y1 ) = d and The distance from F1 to (x2 , y2 ) - the distance from F2 to (x2 , y2 ) = d Standard Form of a Hyperbola: Horizontal Hyperbola Vertical Hyperbola 2 2 2 2 (x − h) (y − k) (y − k) (x − h) 2 − 2 = 1 2 − 2 = 1 a b a b center = (h,k) 2a = distance between vertices c = distance from center to focus c2 = a2 + b2 c eccentricity e = ( e > 1 for a hyperbola) a Conjugate axis = 2b Transverse axis = 2a Horizontal Asymptotes Vertical Asymptotes b a y − k = ± (x − h) y − k = ± (x − h) a b Show how d = 2a 2 (x − 2) y2 Ex. Graph − = 1 4 25 Center: (2, 0) Vertices (4, 0) & (0, 0) Foci (2 ± 29,0) 5 Asymptotes: y = ± (x − 2) 2 Ex. Graph 9y2 − x2 − 6x −10 = 0 9y2 − x2 − 6x = 10 9y2 −1(x2 + 6x + 9) = 10 − 9 2 9y2 −1(x + 3) = 1 2 9y2 1(x + 3) 1 − = 1 1 1 2 y2 x + 3 ( ) 1 1 − = 9 1 Center: (-3, 0) ⎛ 1⎞ ⎛ 1⎞ Vertices −3, & −3,− ⎝⎜ 3⎠⎟ ⎝⎜ 3⎠⎟ ⎛ 10 ⎞ Foci −3,± ⎝⎜ 3 ⎠⎟ 1 Asymptotes: y = ± (x + 3) 3 Hyperbolas can be used in so-called ‘trilateration’ or ‘positioning’ problems. The procedure outlined in the next example is the basis of the Long Range Aid to Navigation (LORAN) system, (outdated now due to GPS) Ex.
    [Show full text]
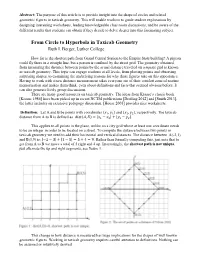
  • From Circle to Hyperbola in Taxicab Geometry
    Abstract: The purpose of this article is to provide insight into the shape of circles and related geometric figures in taxicab geometry. This will enable teachers to guide student explorations by designing interesting worksheets, leading knowledgeable class room discussions, and be aware of the different results that students can obtain if they decide to delve deeper into this fascinating subject. From Circle to Hyperbola in Taxicab Geometry Ruth I. Berger, Luther College How far is the shortest path from Grand Central Station to the Empire State building? A pigeon could fly there in a straight line, but a person is confined by the street grid. The geometry obtained from measuring the distance between points by the actual distance traveled on a square grid is known as taxicab geometry. This topic can engage students at all levels, from plotting points and observing surprising shapes, to examining the underlying reasons for why these figures take on this appearance. Having to work with a new distance measurement takes everyone out of their comfort zone of routine memorization and makes them think, even about definitions and facts that seemed obvious before. It can also generate lively group discussions. There are many good resources on taxicab geometry. The ideas from Krause’s classic book [Krause 1986] have been picked up in recent NCTM publications [Dreiling 2012] and [Smith 2013], the latter includes an extensive pedagogy discussion. [House 2005] provides nice worksheets. Definition: Let A and B be points with coordinates (푥1, 푦1) and (푥2, 푦2), respectively. The taxicab distance from A to B is defined as 푑푖푠푡(퐴, 퐵) = |푥1 − 푥2| + |푦1 − 푦2|.
    [Show full text]