Real Time Measurement in Guadiana River Estuary
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pdfs/ BOE/1938/505/A06178-06181.Pdf (5) Apuntes Históricos De La Universidad De Barcelona (2018)
Revista 2018 DICIEMBRE NÚMERO 12 de Historia de las Vegas Altas —Vegas Altas History Review — Artículos MARINA FATUARTE CORTÉS Reseñando a López Prudencio: “Relieves antiguos” en “Correo de la mañana”, Badajoz, 1925 CRISTIAN GALLEGO MARTÍN-ROMO; ESTEBAN CRUZ HIDALGO Autarquía y condiciones laborales: las reglamentaciones nacionales de trabajo durante el primer franquismo DANIEL CORTÉS GONZÁLEZ Apuntes históricos sobre los Centros de Enseñanza en Don Benito (1885-1977) JESÚS SECO GONZÁLEZ Dimensión social del regadío y la colonización de Vegas Altas Memoria Viva MARÍA JOSÉ SERRANO SUÁREZ Entrevista a Alberto Muñoz Pérez de las Vacas Natushistoria MARÍA INMACULADA FERNÁNDEZ MARTIN; NOELIA RANGEL PRECIADO La Dehesa extremeña. Un recurso didáctico Turismo por... DAVID MARTÍN BERMEJO El Valle de Alagón. Un lugar por descubrir Apartado Literario-Narrativo MARÍA JOSÉ FERNÁNDEZ SÁNCHEZ Viaje a la eternidad FRANCISCO VALDÉS NICOLAU Un delicado y doloroso tema Rincón del Pasado Imágenes para el recuerdo Facsímil: Carta de privilegio del título de Villa a Don Benito (1735) Reseñas Bibliográficas 12 Revista de Historia de las Vegas Altas - Vegas Altas History Review Nº 12 (Diciembre 2018) Una edición del Grupo de Estudios de las Vegas Altas (GEVA) ISSN: 2253-7287 Editada en Don Benito. Disponible online en https://revistadehistoriadelasvegasaltas.com Revista de la Asociación “Torre Isunza” para la Defensa del Patrimonio Histórico y Cultural de Don Benito (http://asociaciontorreisunza.wordpress.com). E-mail de contacto: [email protected] -

The Celts of the Southwestern Iberian Peninsula
e-Keltoi: Journal of Interdisciplinary Celtic Studies Volume 6 The Celts in the Iberian Peninsula Article 9 7-12-2005 The eltC s of the Southwestern Iberian Peninsula Luis Berrocal-Rangel Departamento de Prehistoria y Arqueología, Universidad Autónoma de Madrid Follow this and additional works at: https://dc.uwm.edu/ekeltoi Recommended Citation Berrocal-Rangel, Luis (2005) "The eC lts of the Southwestern Iberian Peninsula," e-Keltoi: Journal of Interdisciplinary Celtic Studies: Vol. 6 , Article 9. Available at: https://dc.uwm.edu/ekeltoi/vol6/iss1/9 This Article is brought to you for free and open access by UWM Digital Commons. It has been accepted for inclusion in e-Keltoi: Journal of Interdisciplinary Celtic Studies by an authorized administrator of UWM Digital Commons. For more information, please contact open- [email protected]. The Celts of the Southwestern Iberian Peninsula Luis Berrocal-Rangel Departamento de Prehistoria y Arqueología Universidad Autónoma de Madrid Abstract Archaeological investigations carried out in the southwestern Iberian Peninsula during recent years have contributed to the identification of the cultural characteristics of its ancient populations, called Keltikoi or Celtici by Ephorus, Herodotus, Strabo and Pliny. From a detailed analysis of the types and distribution of the material culture, references in the Classical sources, epigraphic evidence, contemporary observations, and the presence of an individual decorative style of hand-made pottery, it is now possible to record the specific cultural traits of those native populations that occupied, at least from the end of the fifth century BC, the basins of the Sado and Guadiana Rivers in both Spain and Portugal. -
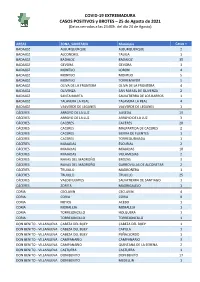
210825 Datos Covid- 19 EXT.Casos+ Y Brotes
COVID-19 EXTREMADURA CASOS POSITIVOS y BROTES – 25 de Agosto de 2021 (Datos cerrados a las 24:00h. del día 24 de Agosto) AREAS ZONA_SANITARIA Municipio Casos + BADAJOZ ALBURQUERQUE ALBURQUERQUE 2 BADAJOZ ALCONCHEL TALIGA 1 BADAJOZ BADAJOZ BADAJOZ 35 BADAJOZ GEVORA GEVORA 1 BADAJOZ MONTIJO LOBON 4 BADAJOZ MONTIJO MONTIJO 5 BADAJOZ MONTIJO TORREMAYOR 5 BADAJOZ OLIVA DE LA FRONTERA OLIVA DE LA FRONTERA 4 BADAJOZ OLIVENZA SAN RAFAEL DE OLIVENZA 2 BADAJOZ SANTA MARTA SALVATIERRA DE LOS BARROS 1 BADAJOZ TALAVERA LA REAL TALAVERA LA REAL 4 BADAJOZ VALVERDE DE LEGANES VALVERDE DE LEGANES 1 CÁCERES ARROYO DE LA LUZ ALISEDA 19 CÁCERES ARROYO DE LA LUZ ARROYO DE LA LUZ 3 CÁCERES CACERES CACERES 20 CÁCERES CACERES MALPARTIDA DE CACERES 2 CÁCERES CACERES SIERRA DE FUENTES 1 CÁCERES CACERES TORREQUEMADA 1 CÁCERES MIAJADAS ESCURIAL 2 CÁCERES MIAJADAS MIAJADAS 10 CÁCERES MIAJADAS VILLAMESIAS 2 CÁCERES NAVAS DEL MADROÑO BROZAS 3 CÁCERES NAVAS DEL MADROÑO GARROVILLAS DE ALCONETAR 2 CÁCERES TRUJILLO MADROÑERA 1 CÁCERES TRUJILLO TRUJILLO 25 CÁCERES VALDEFUENTES SALVATIERRA DE SANTIAGO 1 CÁCERES ZORITA MADRIGALEJO 1 CORIA CECLAVIN CECLAVIN 4 CORIA CORIA CORIA 9 CORIA HOYOS ACEBO 1 CORIA MORALEJA MORALEJA 1 CORIA TORREJONCILLO HOLGUERA 1 CORIA TORREJONCILLO TORREJONCILLO 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY CABEZA DEL BUEY 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY CAPILLA 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY PEÑALSORDO 1 DON BENITO - VILLANUEVA CAMPANARIO CAMPANARIO 3 DON BENITO - VILLANUEVA CAMPANARIO QUINTANA DE LA SERENA 2 DON BENITO - VILLANUEVA CASTUERA CASTUERA 1 DON BENITO - VILLANUEVA DON BENITO DON BENITO 17 DON BENITO - VILLANUEVA DON BENITO MEDELLIN 1 COVID-19 EXTREMADURA CASOS POSITIVOS y BROTES – 25 de Agosto de 2021 (Datos cerrados a las 24:00h. -

Cto Extremadura Infantil-Junior Don Benito, 25 - 26/1/2020
CTO EXTREMADURA INFANTIL-JUNIOR DON BENITO, 25 - 26/1/2020 Prueba 22 Fem., 200m Libre 13 - 17 años 26/01/2020 - 10:43 Listado de inscrito REX 1:59.08 FÁTIMA GALLARDO CARAPETO CASTELLON 29/11/2013 MME 17 1:59.14 FÁTIMA GALLARDO CARAPETO X 01/01/2014 MME 16 1:59.08 FÁTIMA GALLARDO CARAPETO X 01/01/2013 MME 15 2:02.63 FÁTIMA GALLARDO CARAPETO X 01/01/2012 MME 14 2:01.94 FÁTIMA GALLARDO CARAPETO X 01/01/2011 MME 13 2:12.80 FÁTIMA GALLARDO CARAPETO X 01/01/2010 MINIMAS 2007 13: 2:40.00 / MÍNIMAS 2003 17: 2:40.00 / MÍNIMAS 2004 16: 2:43.50 / MÍNIMAS 2005 15: 2:48.00 / MÍNIMAS 2006 14: 2:52.00 Introducir conversión: ESP:Conversion Spanish Rules LICENCIA NOMBRE AÑO CLUB M. REAL PISC M. CONV FECHA LUGAR 1 1108394 SANCHEZ-MIRANDA CABANILLAS A.2005 C.N. Don Benito Acuarun 2:09.70 25m S 2:09.70 22/12/2019 CÁCERES 2 1127489 PEDROSA MOLERO Clara 2004 El Perú Cáceres Wellness 2:10.00 25m S 2:10.00 22/12/2019 CÁCERES 3 1089022 MARTIN BECERRA Ana Maria 2003 C.N. Almendralejo 2:10.61 25m S 2:10.61 18/05/2019 CACERES 4 1100670 GARCIA SANTOS Andrea 2004 C.N. Plasencia 2:11.41 25m S 2:11.41 22/12/2019 CÁCERES 5 1140683 DOMINGUEZ HERNANDEZ Aitana 2005 C.N. Plasencia 2:12.61 25m S 2:12.61 05/05/2019 BADAJOZ 6 1089030 MORON ALONSO Beatriz 2004 C.N. -

Presentation
Presentation Presentation from the 2008 World Water Week in Stockholm ©The Author(s), all rights reserved Stockholm Water Week 2008 Virtual Water and Water Footppyrint: From Theory to Practice Virtual Water and Water Footprint: A Case Study from Spain M. Ramón Llamas§ Alberto Garrido*, Maite M. Aldaya §, Paula Novo*,Roberto RdíRodríguez Cd*Casado*, ClConsuelo VlVarela‐OtOrtega * § Universidad Complutense, Spain *Universidad Politécnica de Madrid, Spain Project Funded by • Sylabus Motivation Objectives Data Results Discussion Motivation • WF + VW are indicators that inform water policy decisions • There are critical issues that the literature has covered only superficially: – The Green‐blue water compp,onents, and drought cycles – Virtual water trade as water policy indicator • A few but crucial methodological issues question hit herto WF+VW evaliluations for SiSpain Objectives 1. Obtain new evaluations of WF and VW at lower scale (provincial) and for different years 2. Evaluate water scarcity in light of the evaluations of WF and VW 3. Distill water policy and farm policy lessons drawn from the WF and VW Data sources 1. Area/yield of 93 crops, rainfed and irrigated, in each province along 9 years (1997‐2005) (Ministry of Agriculture) 2. ETP evaluated for each crop, province and year (Allen et al., 1998; INM, 2007) 3. Blue water estimated as a complement to available green water and checked with Water Authorities 4. Trade of all crop products and years (MITYC, 2007) Results 1. Comparisons from previous evaluations 2. Spanish agricultural and livestock footprints 3. Agricultural Virtual Water Trade 4. Hydrological and economic water productivity 5. Does international agricultural trade increase water use in Spain? 6. -

Alien Species in the Guadiana Estuary
Aquatic Invasions (2009) Volume 4, Issue 3: 501-506 DOI 10.3391/ai.2009.4.3.11 © 2009 The Author(s) Journal compilation © 2009 REABIC (http://www.reabic.net) This is an Open Access article Short communication Alien species in the Guadiana Estuary (SE-Portugal/SW-Spain): Blackfordia virginica (Cnidaria, Hydrozoa) and Palaemon macrodactylus (Crustacea, Decapoda): potential impacts and mitigation measures Maria Alexandra Chícharo1*, Tânia Leitão1, Pedro Range1, Cristina Gutierrez2, Jesus Morales2, Pedro Morais1 and Luís Chícharo1 1CIMAR/CCMAR – Centro de Ciências do Mar, Faculdade de Ciências do Mar e do Ambiente, Campus de Gambelas, Universidade do Algarve, 8005-139 Faro, Portugal 2Instituto Andaluz de Investigación y Formación Agraria, Pesquera, Alimentaria y de la Producción Ecológica (IFAPA) Centro “Agua del Pino”, Ctra. Punta Umbria-Cartaya s/n. 21450 Cartaya, Huelva, España E-mail: [email protected] (MAC), [email protected] (TL), [email protected] (PR), [email protected] (PM), [email protected] (LC), [email protected] (JM), [email protected] (CG) *Corresponding author Received 9 May 2009; accepted in revised form 6 August 2009; published online 10 August 2009 Abstract The cnidarian Blackfordia virginica and the adult of the caridean prawn, Palaemon macrodactylus are first recorded from the Guadiana Estuary. The habitats and environmental conditions under which these species were found are described and the potential impacts and mitigation measures for their introduction are discussed. The first observations of adults of these species were made in July 2008, at the transitional zone of the estuary (brackish area). Most samples taken in the middle-estuary were characterized by large densities of B. -

River Basin Management Plans
EUROPE-INBO PORTO (PORTUGAL) 27 – 30 SEPTEMBER 2011 Tagus River Basin District Administration Administração da Região Hidrográfica do Tejo, I.P. (ARH do Tejo, I.P.) Manuel Lacerda WATER LAW – INSTITUTIONAL FRAMEWORK . Public Administration . National level - National Water Authority (Instituto da Água – INAG) . Regional level - Coordination and Regional Development Commissions . River Basin District level – River Basin District Administrations (Administrações de Região Hidrográfica – ARH) . Local level - Municipalities . Public or private entities . Users Associations . Multipurpose Infrastructures . Advisory bodies . National Water Council . River Basin District Council RIVER BASIN DISTRICT ADMINISTRATIONS (RBDA) IN PORTUGAL MAINLAND ▪ ARH do Norte (North RBDA) . Minho and Lima RB . Cávado, Ave e Leça RB . Douro RB ▪ ARH do Centro (Centre RBDA) . Vouga, Mondego and Lis RB . West Coast RB ▪ ARH do Tejo (Tagus RBDA) . Tagus RB ▪ ARH do Alentejo (Alentejo RBDA) . Sado and Mira RB . Guadiana RB ▪ ARH do Algarve (Algarve RBDA) . Algarve RB TAGUS RBDA AREA AND MAIN FIGURES Portugal ARH do Tejo mainland jurisdiction area Area (km2) 89 271 28 077 (31 %) Population (inhabit.) 9 858 925 3 485 816 (35 %) Municipalities (nr.) 278 107 (38 %) Coastal line (km) 898 261 (32 %) Bathing areas (nr.) 425 124 (29 %) TAGUS – INTERNATIONAL RIVER BASIN DISTRICT . Convention for the Protection and Sustainable Use of Water in the Shared River Basins of Portugal and Spain (Albufeira Convention) . Commission for Implementation and Development of the Convention (CADC) -

Climate Change Effects on the Hydrology of The
Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2018-258-RC1, 2018 HESSD © Author(s) 2018. This work is distributed under the Creative Commons Attribution 4.0 License. Interactive comment Interactive comment on “Climate change effects on the hydrology of the headwaters of the Tagus River: implications for the management of the Tagus-Segura transfer” by Francisco Pellicer-Martínez and José Miguel Martínez-Paz Anonymous Referee #1 Received and published: 2 July 2018 GENERAL COMMENTS The manuscript studies the effects of climate change on the Tagus-Segura water trans- fer. According to the authors, the work constitutes a new contribution because it ana- lyzes the impact of climate change in an inter-basin water transfer from an integrated Printer-friendly version water management perspective. Despite they cite a recent article where the issue has already been addressed (Morote et al., 2017), they explain that their approach includes Discussion paper three new aspects: 1) specific modelling of climate scenarios; 2) hydrological modelling and; 3) simulation of the system management under the current operating rule. C1 In my opinion, despite the subject could be really interesting for the future manage- ment of Tagus-Segura water transfer, the selected methodology does not constitute a HESSD new contribution to the existing literature. Besides, although the estimation of climate change socioeconomic impacts for the case study could be considered as a novelty, it is scarcely developed. Demand curves are mentioned for the first time in the Dis- Interactive cussion section, the methodology to obtain them is not further explained and plots are comment not provided. -

Lisbon, Évora & the Algarve
VBT Itinerary by VBT www.vbt.com Portugal: Lisbon, Évora & the Algarve Bike Vacation + Air Package Cycle into the magnificent heart of the Alentejo and Algarve regions. During your Portugal bike tour, VBT deeply immerses you in spectacular landscapes and a famously welcoming culture. You’ll ride among stunning vineyard-laden vistas past cork forests and olive groves to remarkably preserved hilltop villages and scenic seaside towns. Sample farm-fresh cuisine as the guests of a farmhouse café and delicious wines from local wineries. Straddle the border with Spain when you embark on a Guadiana River cruise. The region’s rich heritage greets you, too, in the UNESCO site of Évora, a stunningly preserved medieval gem, and in ancient Mértola, home to a Moorish mosque steeped in history. Authentic accommodations, including an elegant Algarve retreat, evoke the character of the region, enhancing this unforgettable adventure. 1 / 10 VBT Itinerary by VBT www.vbt.com Cultural Highlights Marvel at the UNESCO World Heritage site of Évora and the eerie Chapel of the Bones in the São Francisco Church Stroll the charming cobbled lanes of hilltop Monsaraz, a stunning village crowned by a medieval castle Cycle Alentejo’s stunning landscapes of sprawling vineyards, cork tree forests and olive groves Roam the hallowed halls of the Moorish medieval mosque in the ancient town of Mértola 2 / 10 VBT Itinerary by VBT www.vbt.com Pedal along the Guadiana River, then cruise its waters by privately chartered river boat Straddle two time zones at the border between Portugal and Spain along the Guadiana River Indulge in the amenities of your elegant Algarve retreat, relaxing in a heated pool and savoring locally sourced meals Taste the delectable flavors of Portugal in the simple ingredients of its rustic cuisine and the famed locally produced wines What to Expect This tour offers a combination of rolling terrain and moderate-to-challenging hills. -

Drought and Ecological Flows in the Lower Guadiana River Basin (Southwest Iberian Peninsula)
water Article Drought and Ecological Flows in the Lower Guadiana River Basin (Southwest Iberian Peninsula) Inmaculada Pulido-Calvo * , Juan Carlos Gutiérrez-Estrada and Víctor Sanz-Fernández Departamento de Ciencias Agroforestales, Escuela Técnica Superior de Ingeniería, Campus El Carmen, Universidad de Huelva, 21007 Huelva, Spain; [email protected] (J.C.G.-E.); [email protected] (V.S.-F.) * Correspondence: [email protected] Received: 13 December 2019; Accepted: 22 February 2020; Published: 2 March 2020 Abstract: Drought temporal characterization is a fundamental instrument in water resource management and planning of basins with dry-summer Mediterranean climate and with a significant seasonal and interannual variability of precipitation regime. This is the case for the Lower Guadiana Basin, where the river is the border between Spain and Portugal (Algarve-Baixo Alentejo-Andalucía Euroregion). For this transboundary basin, a description and evaluation of hydrological drought events was made using the Standardized Precipitation Index (SPI) with monthly precipitation time series of Spanish and Portuguese climatic stations in the study area. The results showed the occurrence of global cycles of about 25–30 years with predominance of moderate and severe drought events. It was observed that the current requirements of ecological flows in strategic water bodies were not satisfied in some months of October to April of years characterized by severe drought events occurring in the period from 1946 to 2015. Therefore, the characterization of the ecological status of the temporary streams that were predominant in this basin should be a priority in the next hydrologic plans in order to identify the relationships between actual flow regimes and habitat attributes, thereby improving environmental flows assessments, which will enable integrated water resource management. -

NOBLES EMPADRONADOS EN EXTREMADURA EN 1829” Por Joaquín Ignacio Polo Miembro De HISPAGEN Febrero De 2005
ÍNDICE ONOMÁSTICO para “NOBLES EMPADRONADOS EN EXTREMADURA EN 1829” Por Joaquín Ignacio Polo Miembro de HISPAGEN Febrero de 2005 NOBLES EMPADRONADOS EN EXTREMADURA EN 1829 es un estudio del Conde de Canilleros y de San Miguel, publicado en 1961 por el INSTITUTO "LUIS DE SALAZAR Y CASTRO" (C. S. I. C.) en un aparte de la Revista Hidalguía. 1 NOTAS El presente Índice Onomástico solamente pretende ser una herramienta de ayuda para el investigador genealógico en las tierras extremeñas, al objeto de poder entrar en la información directamente a través del gentilico. Para una mayor facilidad en las búsquedas, todos los gentilicios se presentan en mayúsculas y sin tilde (p. e. BENITEZ en lugar de Benítez). Los títulos nobiliarios están clasificados tanto por el título (conde, marqués, etc.) como por el nombre del título (CANILLEROS, CASA AYALA, etc.) El título se ha escrito en minúsculas. Las poblaciones se escriben en su grafía normal. NOBLES EMPADRONADOS EN EXTREMADURA EN 1829 es un magnífico estudio del Conde de Canilleros y de San Miguel, que fue publicado el año 1961, por el INSTITUTO "LUIS DE SALAZAR Y CASTRO" (C. S. I. C.) en un aparte de la Revista Hidalguía. ÍNDICE ONOMÁSTICO APELLIDO POBLACIONES ACEDO ................................................................Almendralejo, Malpartida de la Serena, Valle de la Serena ACEVEDO GAMONAL......................................Plasencia ACEVEDO...........................................................Plasencia ADAME ...............................................................Fuente -

The Landforms of Spain
UNIT The landforms k 1 o bo ote Work in your n of Spain Spain’s main geographical features Track 1 Spain’s territory consists of a large part of the Iberian Peninsula, the Canary Islands in the Atlantic Ocean, the Balearic Islands in the Mediterranean Sea and the autonomous cities of Ceuta and Melilla, located on the north coast of Africa. All of Spain’s territory is located in the Northern Hemisphere. Peninsular Spain shares a border with France and Andorra to the north and with Portugal, which is also on the Iberian Peninsula, to the west. The Cantabrian Sea and the Atlantic Ocean border the north and west coast of the Peninsula and the Mediterranean Sea borders the south and east coast. The Balearic Islands are an archipelago in the Mediterranean Sea. The Canary Islands, however, are an archipelago located almost 1 000 kilometres southwest of the Peninsula, in the middle of the Atlantic Ocean, just north of the coast of Africa. Spain is a country with varied terrain and a high average altitude. Spain’s high average altitude is due to the numerous mountain ranges and systems located throughout the country and the fact that a high inner plateau occupies a large part of the Peninsula. The islands are also mostly mountainous and have got significant elevations, especially in the Canary Islands. Northernmost point 60°W 50°W 40°W 30°W 20°W 10°W 0° 10°E 20°E 30°E 40°E 50°E 60°N Southernmost point Easternmost point s and Westernmost point itie y iv ou ct ! a m 50°N r Estaca o S’Esperó point (Menorca), f de Bares, 4° 19’ E d ATLANTIC 43° 47’ N n a L 40°N ltar Gibra Str.