DOCSLIB.ORG

Mental Math: Estimate Sums and Differences

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mental Math: Estimate Sums and Differences RETEACH Workbook Grade 4 P Visit The Learning Site! www.harcourtschool.com S H HSP TTitle_CR_NLG4.indditle_CR_NLG4.indd 1 66/7/07/7/07 33:27:56:27:56 PPMM Copyright © by Harcourt, Inc. All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage and retrieval system, without permission in writing from the publisher. Permission is hereby granted to individuals using the corresponding student’s textbook or kit as the major vehicle for regular classroom instruction to photocopy entire pages from this publication in classroom quantities for instructional use and not for resale. Requests for information on other matters regarding duplication of this work should be addressed to School Permissions and Copyrights, Harcourt, Inc., 6277 Sea Harbor Drive, Orlando, Florida 32887-6777. Fax: 407-345-2418. HARCOURT and the Harcourt Logo are trademarks of Harcourt, Inc., registered in the United States of America and/or other jurisdictions. Printed in the United States of America ISBN 13: 978-0-15-356800-8 ISBN 10: 0-15-356800-3 If you have received these materials as examination copies free of charge, Harcourt School Publishers retains title to the materials and they may not be resold. Resale of examination copies is strictly prohibited and is illegal. Possession of this publication in print format does not entitle users to convert this publication, or any portion of it, into electronic format. 1 2 3 4 5 6 7 8 9 10 018 6 15 14 13 12 11 10 09 08 07 NNL_SEGr4.inddL_SEGr4.indd template1template1 66/7/07/7/07 33:04:36:04:36 PPMM Unit 1: UNDERSTAND WHOLE NUMBERS Unit 2: MULTIPLICATION AND DIVISION AND OPERATIONS FACTS Chapter 1: Understand Place Value Chapter 4: Multiplication and Division Facts 1.1 Place Value Through 4.1 Algebra: Relate Hundred Thousands ............RW1 Operations ..................... RW19 1.2 Model Millions ..................RW2 4.2 Algebra: Relate Multiplication 1.3 Place Value Through and Division ................... RW20 Millions ...........................RW3 4.3 Multiply and Divide 1.4 Compare Whole Numbers. ....RW4 Facts Through 5 ............... RW21 1.5 Order Whole Numbers. ........RW5 4.4 Multiply and Divide 1.6 Problem Solving Workshop Facts Through 10 ............. RW22 Strategy: Use Logical 4.5 Multiplication Table Reasoning ........................RW6 Through 12 .................... RW23 4.6 Patterns on the Chapter 2: Add and Subtract Whole Multiplication Table .......... RW24 Numbers 4.7 Problem Solving Workshop 2.1 Algebra: Relate Addition Skill: Choose the and Subtraction .................RW7 Operation ...................... RW25 2.2 Round Whole Numbers 4.8 Algebra: Find Missing Through Millions ...............RW8 Factors .......................... RW26 2.3 Mental Math: Estimate Sums and Differences ..........RW9 Chapter 5: Algebra: Use Multiplication and 2.4 Mental Math Division Facts Strategies ...................... RW10 5.1 Multiplication 2.5 Problem Solving Workshop Properties ...................... RW27 Skill: Estimate or 5.2 Multiplication and Division Exact Answer .................. RW11 Expressions ..................... RW28 2.6 Add and Subtract 3-Digit and 5.3 Order of Operations ......... RW29 4-Digit Numbers. .............. RW12 5.4 Multiplication and Division 2.7 Choose a Method. ............ RW13 Equations ...................... RW30 5.5 Problem Solving Workshop Chapter 3: Algebra: Use Addition and Strategy: Predict and Test ... RW31 Subtraction 5.6 Explore Inequalities .......... RW32 3.1 Addition Properties .......... RW14 5.7 Patterns: Find a Rule ......... RW33 3.2 Write and Evaluate Expressions ..................... RW15 3.3 Addition and Subtraction Equations ..................... RW16 3.4 Problem Solving Workshop Strategy: Work Backward ... RW17 3.5 Patterns: Find a Rule ........ RW18 GG4-NL4-NL TTOC_TE.inddOC_TE.indd 1 66/7/07/7/07 33:44:02:44:02 PPMM Unit 3: TIME, TEMPERATURE, AND DATA Unit 4: MULTIPLY BY 1-DIGIT AND 2-DIGIT NUMBERS Chapter 6: Time and Temperature 6.1 Telling Time .................... RW34 Chapter 9: Multiply by 1-Digit Numbers 6.2 Elapsed Time .................. RW35 9.1 Mental Math: Multiplication 6.3 Elapsed Time on Patterns ........................ RW57 a Calendar ..................... RW36 9.2 Mental Math: Estimate 6.4 Algebra: Change Units Products ........................ RW58 of Time ......................... RW37 9.3 Model 2-Digit by 1-Digit 6.5 Problem Solving Workshop Multiplication ................. RW59 Skill: Sequence 9.4 Record 2-Digit by 1-Digit Informaiton .................... RW38 Multiplication ................. RW60 6.6 Temperature ................... RW39 9.5 Multiply 3-Digit and 4-Digit 6.7 Explore Negative Numbers .. RW40 Numbers and Money ......... RW61 9.6 Multiply with Zeros .......... RW62 Chapter 7: Collect and Organize Data 9.7 Problem Solving Workshop 7.1 Collect and Organize Data .. RW41 Skill: Evaluate 7.2 Venn Diagrams ................ RW42 Reasonableness ............... RW63 7.3 Find Mean, Median, and Mode ...................... RW43 Chapter 10: Multiply by 2-Digit Numbers 7.4 Line Plots ....................... RW44 10.1 Mental Math: Multiplication 7.5 Choose a Reasonable Patterns ........................ RW64 Scale and Interval ............. RW45 10.2 Multiply by Tens .............. RW65 7.6 Problem Solving Workshop 10.3 Mental Math: Estimate Skill: Make Products ........................ RW66 Generalizations ............... RW46 10.4 Problem Solving Workshop Strategy: Solve a Chapter 8: Interpret and Graph Data Simpler Problem .............. RW67 8.1 Bar Graphs ..................... RW47 10.5 Model 2-Digit by 2-Digit 8.2 Make Bar and Double-Bar Multiplication ................. RW68 Graphs .......................... RW48 10.6 Record 2-Digit by 2-Digit 8.3 Circle Graphs .................. RW49 Multiplication ................. RW69 8.4 Algebra: Use a Coordinate 10.7 Multiply 2-Digit and 3-Digit Grid ............................. RW50 Numbers and Money ......... RW70 8.5 Line Graphs .................... RW51 10.8 Choose a Method ............. RW71 8.6 Make Line Graphs ............ RW52 10.9 Problem Solving Workshop 8.7 Problem Solving Workshop Skill: Multistep Problems .... RW72 Strategy: Make a Graph ..... RW53 8.8 Choose an Appropriate Graph ........... RW54 8.9 Algebra: Graph Relationships .................. RW55 8.10 Problem Solving Workshop Skill: Identify Relationships ... RW56 GG4-NL4-NL TTOC_TE.inddOC_TE.indd 2 66/7/07/7/07 33:44:07:44:07 PPMM Unit 5: DIVIDE BY 1-DIGIT AND Unit 6: FRACTIONS AND DECIMALS 2-DIGIT DIVISORS Chapter 15: Understand Fractions and Mixed Chapter 11: Understand Division Numbers 11.1 Divide with Remainders ..... RW73 15.1 Read and Write Fractions ... RW94 11.2 Model 2-Digit by 1-Digit 15.2 Model Equivalent Division ......................... RW74 Fractions ....................... RW95 11.3 Record 2-Digit by 1-Digit 15.3 Compare and Order Division ......................... RW75 Fractions ....................... RW96 11.4 Problem Solving Workshop 15.4 Read and Write Mixed Strategy: Draw a Diagram ... RW76 Numbers ....................... RW97 11.5 Mental Math: 15.5 Compare and Order Division Patterns .............. RW77 Mixed Numbers ............... RW98 11.6 Mental Math: 15.6 Problem Solving Workshop Estimate Quotients ........... RW78 Skill: Sequence 11.7 Place the First Digit .......... RW79 Information .................... RW99 Chapter 12: Practice Division Chapter 16: Add and Subtract Fractions and 12.1 Problem Solving Workshop Mixed Numbers Skill: Interpret the 16.1 Model Addition ..............RW100 Remainder ..................... RW80 16.2 Model Subtraction ..........RW101 12.2 Divide 3-Digit Numbers 16.3 Record Addition and Money .................... RW81 and Subtraction ..............RW102 12.3 Zeros in Division .............. RW82 16.4 Problem Solving Workshop 12.4 Choose a Method ............. RW83 Strategy: Write an Equation ......................RW103 Chapter 13: Divide by 2-Digit Divisors 16.5 Add and Subtract 13.1 Estimate Quotients ........... RW84 Mixed Numbers ..............RW104 13.2 Model Division by 2-Digit 16.6 Model Addition and Divisors ......................... RW85 Subtraction of Unlike 13.3 Record Division ............... RW86 Fractions ......................RW105 13.4 Adjusting Quotients .......... RW87 13.5 Problem Solving Workshop Chapter 17: Understand Decimals and Place Skill: Too Much/Too Little Value Information .................... RW88 17.1 Relate Fractions and Decimals .................RW106 Chapter 14: Number Theory and Patterns 17.2 Decimals to Thousandths ... RW107 14.1 Factors and Multiples ........ RW89 17.3 Equivalent Decimals .........RW108 14.2 Divisibility Rules ............... RW90 17.4 Relate Mixed Numbers 14.3 Prime and Composite and Decimals .................RW109 Numbers ....................... RW91 17.5 Compare and 14.4 Number Patterns .............. RW92 Order Decimals ...............RW110 14.5 Problem Solving Workshop 17.6 Problem Solving Workshop Strategy: Find a Pattern ..... RW93 Skill: Draw Conclusions .....RW111 GG4-NL4-NL TTOC_TE.inddOC_TE.indd 3 66/7/07/7/07 33:44:12:44:12 PPMM Chapter 18: Add and Subtract Decimals and Unit 8: MEASUREMENT AND PROBABILITY Money 18.1 Round Decimals ..............RW112 18.2 Estimate Decimal Sums Chapter 22: Customary and Metric Measurement and Differences ..............RW113 22.1 Measure Fractional Parts ... RW139 18.3 Model Addition ..............RW114 22.2 Algebra: Change 18.4 Model
Load more

Recommended publications
  • Gladstone and the Bank of England: a Study in Mid-Victorian Finance, 1833-1866
    GLADSTONE AND THE BANK OF ENGLAND: A STUDY IN MID-VICTORIAN FINANCE, 1833-1866 Patricia Caernarv en-Smith, B.A. Thesis Prepared for the Degree of MASTER OF ARTS UNIVERSITY OF NORTH TEXAS May 2007 APPROVED: Denis Paz, Major Professor Adrian Lewis, Committee Member and Chair of the Department of History Laura Stern, Committee Member Sandra L. Terrell, Dean of the Robert B. Toulouse School of Graduate Studies Caernarven-Smith, Patricia. Gladstone and the Bank of England: A Study in Mid- Victorian Finance, 1833-1866. Master of Arts (History), May 2007, 378 pp., 11 tables, bibliography, 275 titles. The topic of this thesis is the confrontations between William Gladstone and the Bank of England. These confrontations have remained a mystery to authors who noted them, but have generally been ignored by others. This thesis demonstrates that Gladstone’s measures taken against the Bank were reasonable, intelligent, and important for the development of nineteenth-century British government finance. To accomplish this task, this thesis refutes the opinions of three twentieth-century authors who have claimed that many of Gladstone’s measures, as well as his reading, were irrational, ridiculous, and impolitic. My primary sources include the Gladstone Diaries, with special attention to a little-used source, Volume 14, the indexes to the Diaries. The day-to-day Diaries and the indexes show how much Gladstone read about financial matters, and suggest that his actions were based to a large extent upon his reading. In addition, I have used Hansard’s Parliamentary Debates and nineteenth-century periodicals and books on banking and finance to understand the political and economic debates of the time.
    [Show full text]
  • The-Way-Into-The-Holiest-FB-Meyer
    The Way Into the Holiest by F. B. Meyer Christian Classics Ethereal Library About The Way Into the Holiest by F. B. Meyer Title: The Way Into the Holiest URL: http://www.ccel.org/ccel/meyer/into_holiest.html Author(s): Meyer, F.B. (1847-1929) Publisher: Grand Rapids, MI: Christian Classics Ethereal Library Rights: Copyright Christian Classics Ethereal Library Date Created: 2000-07-09 CCEL Subjects: All; Bible; LC Call no: BS2775 LC Subjects: The Bible New Testament Special parts of the New Testament The Way Into the Holiest F. B. Meyer Table of Contents About This Book. p. ii THE WAY INTO THE HOLIEST:. p. 1 PREFACE.. p. 1 I. THE WORD OF GOD.. p. 2 II. THE DIGNITY OF CHRIST. p. 6 III. THE GLORY OF CHRIST©S OFFICE. p. 8 IV. DRIFTING. p. 12 V. ªWHAT IS MAN?º. p. 16 VI. ªPerfect through sufferingsº. p. 20 VII. THE DEATH OF DEATH. p. 23 VIII. CHRIST©S MERCIFUL AND FAITHFUL HELP. p. 26 IX. A WARNING AGAINST UNBELIEF. p. 30 X. THE GOSPEL OF REST. p. 36 XI. THE WORD OF GOD AND ITS EDGE. p. 40 XII. TIMELY AND NEEDED HELP. p. 44 XIII. GETHSEMANE. p. 48 XIV. IMPOSSIBLE TO RENEW TO REPENTANCE . p. 53 XV. THE ANCHORAGE OF THE SOUL.. p. 56 XVI. THE PRIESTHOOD OF CHRIST. p. 60 XVII. THE SUPERLATIVE GREATNESS OF CHRIST. p. 63 XVIII. THE TRUE TABERNACLE . p. 67 XIX. THE TWO COVENANTS. p. 71 XX. THE HEAVENLY THINGS THEMSELVES.. p. 75 XXI. TEACHING BY CONTRAST. p. 79 XXII. THE BLOOD OF CHRIST.
    [Show full text]
  • The Western, Media, and Masculinity by Norman M. Gendelman A
    Coming Home: The Western, Media, and Masculinity By Norman M. Gendelman A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Film & Media in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Kristen Whissel, Chair Professor Mary Ann Doane Associate Professor Abigail De Kosnik Professor Emeritus Scott Simmon Fall 2020 Copyright 2020 by Norman Matthew Gendelman 1 Abstract Coming Home: The Western, Media, and Masculinity by Norman Matthew Gendelman Doctor of Philosophy in Film & Media University of California, Berkeley Professor Kristin Whissel, Chair In its analysis of four postwar Westerns (the films The Last Sunset and Gunman’s Walk, and the television Westerns Have Gun—Will Travel and The Rifleman), this dissertation finds a contradictory ideological strain intrinsic to the genre’s frontier legacy, as well as a critical semiosis specific to its production era. By centralizing the postwar era’s domestic concerns over and against the genre’s typical emphasis on the frontier mythos associated with Theodore Roosevelt, these Westerns subvert the stereotypical frontier/civilization dyad. By reconceiving the genre in a way that privileges “civilization” over “frontier,” this dissertation shows that the crucible of “savage” Nature, which formerly determined the exceptionality of the Westerner’s masculine character (as a synecdoche for an exceptional national one), is a cultural production that turns against civilization itself. Denuded of their naturalizing origin, and depicted as social productions within the dramatic action, the gunmen protagonists of each of these four Westerns additionally appear as complex gender constructions. By juxtaposing allusions from each Western to the ideological and aesthetic history of the genre and the socio-political context of the postwar era, the dissertation approaches the Cold War era as similarly mythological, constructed, and contradictory.
    [Show full text]
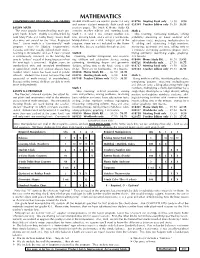
  • MATHEMATICS COMPREHENSIVE PROGRAMS - ALL GRADES Student Workbooks Are Used in Grades 1-3 Only 018726 Meeting Book Only 13.50 8 50
    MATHEMATICS COMPREHENSIVE PROGRAMS - ALL GRADES Student Workbooks are used in grades 1-3 only 018726 Meeting Book only 13.50 8 .50 and contain student materials, flash cards and 021349 Teacher Edition only 59.50 36 .95 SAXON MATH practice pages. The Math K Home Study Kit The most popular homeschooling math pro- contains teacher edition and meeting book. Math 2 gram hands down! Highly recommended by Math 1, 2, and 3 kits contain teacher edi- Skip counting; comparing numbers; solving both Mary Pride and Cathy Duffy, Saxon Math tion, meeting book, and a set of 2 workbooks. problems; mastering all basic addition and also wins our award for the “Most Requested Manipulatives are a vital, integral part of the subtraction facts; mastering multiplication to Text.” Saxon math is a “user-friendly” math program; these are not included in the Home 5; adding and subtracting 2-digit numbers; program - even for Algebra, Trigonometry, Study Kits, but are available through us also. measuring; perimeter and area; telling time to Calculus and other usually difficult math topics. 5 minutes; identifying geometric shapes; iden- Learning is incremental and each new concept Math K tifying symmetry; identifying angles; graphing. is continuously reviewed, so the learning has Counting, number recognition, and sequenc- 132 lessons. time to “sink in” instead of being forgotten when ing; addition and subtraction stories; sorting; 018400 Home Study Kit . 96.50 59 .95 the next topic is presented. Higher scores on patterning, identifying shapes and geometric 001526 Workbooks only . 27.50 16 .75 standardized tests and increased enrollments designs; telling time to the hour; using a cal- 018727 Meeting Book only 13.50 8 .50 in upper-level math and science classes have endar.
    [Show full text]
  • The Altering Eye: Contemporary International Cinema 2009
    Repositorium für die Medienwissenschaft Robert Phillip Kolker The Altering Eye: Contemporary International Cinema 2009 https://doi.org/10.25969/mediarep/4111 Veröffentlichungsversion / published version Buch / book Empfohlene Zitierung / Suggested Citation: Kolker, Robert Phillip: The Altering Eye: Contemporary International Cinema. Cambridge: Open Book Publishers 2009. DOI: https://doi.org/10.25969/mediarep/4111. Erstmalig hier erschienen / Initial publication here: https://doi.org/10.11647/OBP.0002 Nutzungsbedingungen: Terms of use: Dieser Text wird unter einer Creative Commons - This document is made available under a creative commons - Namensnennung - Nicht kommerziell - Keine Bearbeitungen 2.0/ Attribution - Non Commercial - No Derivatives 2.0/ License. For Lizenz zur Verfügung gestellt. Nähere Auskünfte zu dieser Lizenz more information see: finden Sie hier: https://creativecommons.org/licenses/by-nc-nd/2.0/ https://creativecommons.org/licenses/by-nc-nd/2.0/ Robert Phillip Kolker The Altering Eye Contemporary International Cinema THE ALTERING EYE Robert Kolker is Emeritus Professor of English at the University of Maryland and Lecturer in Media Studies at the University of Virginia. His works include A Cinema of Loneliness: Penn, Stone, Kubrick, Scorsese, Spielberg Altman; Bernardo Bertolucci; Wim Wenders (with Peter Beicken); Film, Form and Culture; Media Studies: An Introduction; editor of Alfred Hitchcock’s Psycho: A Casebook; Stanley Kubrick’s 2001: A Space Odyssey: New Essays and The Oxford Handbook of Film and Media Studies. http://www.virginia.edu/mediastudies/people/adjunct.html Robert Phillip Kolker THE ALTERING EYE Contemporary International Cinema Revised edition with a new preface and an updated bibliography Cambridge 2009 Published by 40 Devonshire Road, Cambridge, CB1 2BL, United Kingdom http://www.openbookpublishers.com First edition published in 1983 by Oxford University Press.
    [Show full text]
  • Keeping Meaning in Proportion: the Multiplication Table As a Case of Pedagogical Bridging Tools
    See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/277289221 Keeping meaning in proportion: The multiplication table as a case of pedagogical bridging tools. Unpublished doctoral dissertation Article · January 2004 CITATIONS READS 15 154 1 author: Dor Abrahamson University of California, Berkeley 157 PUBLICATIONS 1,498 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects: relation between physical and conceptual activity View project EDUC 222C: Design-Based Research Forum View project All content following this page was uploaded by Dor Abrahamson on 18 July 2015. The user has requested enhancement of the downloaded file. NORTHWESTERN UNIVERSITY Keeping Meaning in Proportion: The Multiplication Table as a Case of Pedagogical Bridging Tools A DISSERTATION SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS for the degree DOCTOR OF PHILOSOPHY Field of Education and Social Policy – Learning Sciences By Dor Abrahamson EVANSTON, ILLINOIS June, 2004 2 © Copyright by Dor Abrahamson 2004 All Rights Reserved ii 3 ABSTRACT Keeping Meaning in Proportion: The Multiplication Table as a Case of Pedagogical Bridging Tools Dor Abrahamson The broad agenda of this dissertation is the design of mathematics curricula for elementary and middle-school students to build meaning for and fluency with mathematical concepts. The paradigm of the work is design research, which combines empirical and theoretical studies. The empirical substance of this dissertation is a set of studies that were implementations of an experimental curricular unit for 5th-grade students learning the domain of ratio and proportion. The theoretical component of this paper is the apprehending zone (Fuson & Abrahamson, 2004a), a Piagetian–Vygotskiian conceptual–practical model of design, teaching, and learning in mathematics classrooms.
    [Show full text]