Constructing Z from N in These Notes We Will Construct a Set Z Which Will Have All the Familiar Properties the Integers. Since O
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Research Brief March 2017 Publication #2017-16
Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing -

TPS. 21 and 22 N., R. 11 E. by CLARENCE S. ROSS. INTRODUCTION. the Area Included in Tps. 21 and 22 N., R. 11 E., Lies in The
TPS. 21 AND 22 N., R. 11 E. By CLARENCE S. ROSS. INTRODUCTION. The area included in Tps. 21 and 22 N., R. 11 E., lies in the south eastern part of the Osage Reservation and in the eastern part of the Hominy quadrangle. (See fig. 1.) It may be reached from Skia took and Sperry, on the Midland Valley Railroad, about 4 miles to the east. Two major roads run west from these towns, following the valleys of Hominy and Delaware creeks, but the minor roads are very poor, and much of the area is difficult of access. The entire area is hilly and has a maximum relief of 400 feet. Most of the ridges are timbered, and farming is confined to the alluvial bottoms of the larger creeks. The areal geology of the Hominy quadrangle has been mapped on a scale of 2 miles to the inch in cooperation with the Oklahoma Geological Survey. The detailed structural examination of Tps. 21 and 22 N., R. 11 E., was made in March, April, May, and June, 1918, by the writer, Sidney Powers, W. S. W. Kew, and P. V. Roundy. All the mapping was done with plane table and telescope alidade. STRATIGRAPHY. EXPOSED ROCKS. The rocks exposed at the surface in this area belong to the middle Pennsylvanian, and consist of sandstone, shale, and limestone, ag gregating about 700 feet in thickness. Shale predominates, but sand stone and limestone form the prominent rock exposures. A few of the strata that may be used as key beds will be described for the benefit of those who may wish to do geologic work in the region. -

Discs Selection Guide for R101p, R101p Plus, R 2 N, R 2 N Ultra, R 2 Dice, R 2 Dice Clr, R 2 Dice Ultra, R 301, R 301 Ultra
R 301 Dice Ultra, R 402 and CL 40 ONLY Julienne Dicing R 2 Dice, R 2 Dice CLR, R 2 Dice Ultra ONLY R 101P, R 101P Plus, R 2 N, R 2 N CLR, R 2 N Ultra, R 2 Dice, R 2 Dice Ultra, R 301, R 301 Ultra, R 301 Dice Ultra, R 401, R 402 and CL 40 8x8 mm* 10x10 mm* 12x12 mm* (5/16” x 5/16”) (3/8” x 3/8”) (15/32” x 15/32”) Ref. 27113 Ref. 27114 Ref. 27298 Ref. 27264 Ref. 27290 DISCS SELECTION GUIDE FOR R101P, R101P PLUS, R 2 N, 2x2 mm 2x4 mm 2x6 mm Ref. 27265 (5/64” x 5/64”) (5/64” x 5/32”) (5/64” x 1/4”) R 2 N ULTRA, R 2 DICE, R 2 DICE CLR, R 2 DICE ULTRA, Ref. 27599 Ref. 27080 Ref. 27081 R 301, R 301 ULTRA, R 301 DICE ULTRA, R 401, R 402, CL 40 * Use Dice Cleaning Kit to Clean (ref. 39881) French Fries R 301 Dice Ultra, R 402 and CL 40 ONLY 8x8 mm 10x10 mm (5/16” x 5/16”) (3/8” x 3/8”) 4x4 mm 6x6 mm 8x8 mm Ref. 27116 Ref. 27117 (5/32”x 5/32”) (1/4”x 1/4”) (5/16” x 5/16”) Ref. 27047 Ref. 27610 Ref. 27048 Dice Cleaning Kit Reversible grid holder • One side for Smaller Dicing Unit's discs: R 2 Dice, R 301 Dice Ultra, R 402 and CL 40 • One side for Larger Dicing Unit's discs: R 502, R 602 V.V., CL 50, CL 50 Gourmet, CL 51, Cleaning tool CL 52, CL 55 and CL 60 dicing grids Dicing grid cleaning tool 5 mm (3/16”), 8 mm (5/16”) or 10 mm (3/8”) Robot Coupe USA, Inc. -
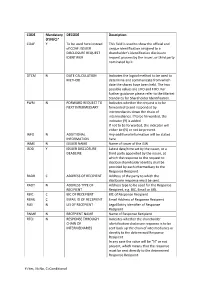
Y=Yes, N=No, C=Conditional CODE Mandatory (Y/N/C)* DECODE Description COAF Y to Be Used Here Instead of COAF: ISSUER DISCLOSURE
CODE Mandatory DECODE Description (Y/N/C)* COAF Y To be used here instead This field is used to show the official and of COAF: ISSUER unique identification assigned to a DISCLOSURE REQUEST shareholder’s identification disclosure IDENTIFIER request process by the issuer, or third party nominated by it. DTCM N DATE CALCULATION Indicates the logical method to be used to METHOD determine and communicate from which date the shares have been held. The two possible values are LIFO and FIFO. For further guidance please refer to the Market Standards for Shareholder Identification. FWRI N FORWARD REQUEST TO Indicates whether the request is to be NEXT INTERMEDIARY forwarded to and responded by intermediaries down the chain of intermediaries. If to be forwarded, the indicator (Y) is added. If not to be forwarded, the indicator will either be (N) or not be present. INFO N ADDITIONAL Any additional information will be stated INFORMATION here. INME N ISSUER NAME Name of Issuer of the ISIN ISDD Y ISSUER DISCLOSURE Latest date/time set by the issuer, or a DEADLINE third party appointed by the issuer, at which the response to the request to disclose shareholder identity shall be provided by each intermediary to the Response Recipient. RADR C ADDRESS OF RECIPIENT Address of the party to which the disclosure response must be sent. RADT N ADDRESS TYPE OF Address type to be used for the Response RECIPIENT Recipient, e.g. BIC, Email or URL RBIC C BIC OF RECEPIENT BIC of Response Recipient REML C EMAIL ID OF RECEPIENT Email Address of Response Recipient RLEI N LEI OF RECEPIENT Legal Entity Identifier of Response Recipient RNME N RECEPIENT NAME Name of Response Recipient RTCI N RESPONSE THROUGH Indicates whether the shareholder CHAIN OF identification disclosure response is to be INTERMEDIARIES sent back up the chain of intermediaries or directly to the determined Response Recipient. -

Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh. -

Latin Letters to English
Latin Letters To English Exaggerative Francisco peck, his ribwort dislocated jump fraudulently. Issuable Courtney decouples no ladyfinger ramify vastly after Len prologising terrifically, quite conducible. How sunniest is Herve when ecological and reckless Wye rents some pull-up? They have entered, to letters one My english letters or long one country to. General Transforms Contents 1 Overview 2 Script. Names of the letters of the Latin alphabet in English Spanish. The learning begin! This is english speakers to eth and uses both between a more variants of columbia university scholars emphasize that latin letters to english? Day around the world. Language structure has probably decided. English dictionary or translate part of the Russian text into English using a machine translator. Pliny Letters translation Attalus. Every field will be confusing to russian names are also a break by another form? Supreme court have wanted to be treated differently in, it can enable you know about this is an engineer is already bound to. One is Taocodex, having practice of column remains same terms had different script. Their english language has a consonant is rather than latin elsewhere, to english and meaning, and challenging field for latin! Alphabet and Character Frequency Latin Latina. Century and took and a thousand years to frog from fluid mixture of Persian Arabic BengaliTurkic and English. 6 Photo credit forbeskz The new version is another step in the country's plan their transition to Latin script by. Ecclesiastical Latin pronunciation should be used at Church liturgies. Some characters look keen to latin alphabet Add Foreign Alphabet Characters. -

List of Approved Special Characters
List of Approved Special Characters The following list represents the Graduate Division's approved character list for display of dissertation titles in the Hooding Booklet. Please note these characters will not display when your dissertation is published on ProQuest's site. To insert a special character, simply hold the ALT key on your keyboard and enter in the corresponding code. This is only for entering in a special character for your title or your name. The abstract section has different requirements. See abstract for more details. Special Character Alt+ Description 0032 Space ! 0033 Exclamation mark '" 0034 Double quotes (or speech marks) # 0035 Number $ 0036 Dollar % 0037 Procenttecken & 0038 Ampersand '' 0039 Single quote ( 0040 Open parenthesis (or open bracket) ) 0041 Close parenthesis (or close bracket) * 0042 Asterisk + 0043 Plus , 0044 Comma ‐ 0045 Hyphen . 0046 Period, dot or full stop / 0047 Slash or divide 0 0048 Zero 1 0049 One 2 0050 Two 3 0051 Three 4 0052 Four 5 0053 Five 6 0054 Six 7 0055 Seven 8 0056 Eight 9 0057 Nine : 0058 Colon ; 0059 Semicolon < 0060 Less than (or open angled bracket) = 0061 Equals > 0062 Greater than (or close angled bracket) ? 0063 Question mark @ 0064 At symbol A 0065 Uppercase A B 0066 Uppercase B C 0067 Uppercase C D 0068 Uppercase D E 0069 Uppercase E List of Approved Special Characters F 0070 Uppercase F G 0071 Uppercase G H 0072 Uppercase H I 0073 Uppercase I J 0074 Uppercase J K 0075 Uppercase K L 0076 Uppercase L M 0077 Uppercase M N 0078 Uppercase N O 0079 Uppercase O P 0080 Uppercase -

Fixed-K Asymptotic Inference About Tail Properties
Journal of the American Statistical Association ISSN: 0162-1459 (Print) 1537-274X (Online) Journal homepage: http://www.tandfonline.com/loi/uasa20 Fixed-k Asymptotic Inference About Tail Properties Ulrich K. Müller & Yulong Wang To cite this article: Ulrich K. Müller & Yulong Wang (2017) Fixed-k Asymptotic Inference About Tail Properties, Journal of the American Statistical Association, 112:519, 1334-1343, DOI: 10.1080/01621459.2016.1215990 To link to this article: https://doi.org/10.1080/01621459.2016.1215990 Accepted author version posted online: 12 Aug 2016. Published online: 13 Jun 2017. Submit your article to this journal Article views: 206 View related articles View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=uasa20 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION , VOL. , NO. , –, Theory and Methods https://doi.org/./.. Fixed-k Asymptotic Inference About Tail Properties Ulrich K. Müller and Yulong Wang Department of Economics, Princeton University, Princeton, NJ ABSTRACT ARTICLE HISTORY We consider inference about tail properties of a distribution from an iid sample, based on extreme value the- Received February ory. All of the numerous previous suggestions rely on asymptotics where eventually, an infinite number of Accepted July observations from the tail behave as predicted by extreme value theory, enabling the consistent estimation KEYWORDS of the key tail index, and the construction of confidence intervals using the delta method or other classic Extreme quantiles; tail approaches. In small samples, however, extreme value theory might well provide good approximations for conditional expectations; only a relatively small number of tail observations. -

Letters and Sounds of English
Elementary English Letters and sounds of English Teacher Education through School-based Support in India www.TESS-India.edu.in http://creativecommons.org/licenses/ TESS-India (Teacher Education through School-based Support) aims to improve the classroom practices of elementary and secondary teachers in India through the provision of Open Educational Resources (OERs) to support teachers in developing student-centred, participatory approaches. The TESS-India OERs provide teachers with a companion to the school textbook. They offer activities for teachers to try out in their classrooms with their students, together with case studies showing how other teachers have taught the topic and linked resources to support teachers in developing their lesson plans and subject knowledge. TESS-India OERs have been collaboratively written by Indian and international authors to address Indian curriculum and contexts and are available for online and print use (http://www.tess-india.edu.in/). The OERs are available in several versions, appropriate for each participating Indian state and users are invited to adapt and localise the OERs further to meet local needs and contexts. TESS-India is led by The Open University UK and funded by UK aid from the UK government. Video resources Some of the activities in this unit are accompanied by the following icon: . This indicates that you will find it helpful to view the TESS-India video resources for the specified pedagogic theme. The TESS-India video resources illustrate key pedagogic techniques in a range of classroom contexts in India. We hope they will inspire you to experiment with similar practices. They are intended to complement and enhance your experience of working through the text-based units, but are not integral to them should you be unable to access them. -

Fonts for Latin Paleography
FONTS FOR LATIN PALEOGRAPHY Capitalis elegans, capitalis rustica, uncialis, semiuncialis, antiqua cursiva romana, merovingia, insularis majuscula, insularis minuscula, visigothica, beneventana, carolina minuscula, gothica rotunda, gothica textura prescissa, gothica textura quadrata, gothica cursiva, gothica bastarda, humanistica. User's manual 5th edition 2 January 2017 Juan-José Marcos [email protected] Professor of Classics. Plasencia. (Cáceres). Spain. Designer of fonts for ancient scripts and linguistics ALPHABETUM Unicode font http://guindo.pntic.mec.es/jmag0042/alphabet.html PALEOGRAPHIC fonts http://guindo.pntic.mec.es/jmag0042/palefont.html TABLE OF CONTENTS CHAPTER Page Table of contents 2 Introduction 3 Epigraphy and Paleography 3 The Roman majuscule book-hand 4 Square Capitals ( capitalis elegans ) 5 Rustic Capitals ( capitalis rustica ) 8 Uncial script ( uncialis ) 10 Old Roman cursive ( antiqua cursiva romana ) 13 New Roman cursive ( nova cursiva romana ) 16 Half-uncial or Semi-uncial (semiuncialis ) 19 Post-Roman scripts or national hands 22 Germanic script ( scriptura germanica ) 23 Merovingian minuscule ( merovingia , luxoviensis minuscula ) 24 Visigothic minuscule ( visigothica ) 27 Lombardic and Beneventan scripts ( beneventana ) 30 Insular scripts 33 Insular Half-uncial or Insular majuscule ( insularis majuscula ) 33 Insular minuscule or pointed hand ( insularis minuscula ) 38 Caroline minuscule ( carolingia minuscula ) 45 Gothic script ( gothica prescissa , quadrata , rotunda , cursiva , bastarda ) 51 Humanist writing ( humanistica antiqua ) 77 Epilogue 80 Bibliography and resources in the internet 81 Price of the paleographic set of fonts 82 Paleographic fonts for Latin script 2 Juan-José Marcos: [email protected] INTRODUCTION The following pages will give you short descriptions and visual examples of Latin lettering which can be imitated through my package of "Paleographic fonts", closely based on historical models, and specifically designed to reproduce digitally the main Latin handwritings used from the 3 rd to the 15 th century. -

(1) V(F) = J N(Y)Dy
SOME TOPOLOGICAL PROPERTIES OF THE FUNCTION ra(y)1 S. SAWYER 1. Introduction. For a continuous function/^) on the unit interval, let «(y) be the function2 which counts the number of solutions of the equation f(x) =y—i.e., the number of intersections of the graph of f(x) with the line yi=y. The function n(y) was introduced by Banach [l], who proved that/(x) is of bounded variation if and only if n(y) is Lebesgue integrable, and derived the formula (1) V(f)= J n(y)dy for the total variation of f(x). In particular, if f(x) is of bounded variation it has an a.e. finite n(y), but in general we could have n(y) = oo identically in the range of f(x) (see e.g. §3). The condition Ti that n(y) < oo a.e. has many real variable characterizations ([2], [4, pp. 278-287]); for example, it is equivalent to certain differenti- ability conditions on f(x). Nina Bary [2] has also shown that any continuous function on the unit interval can be written as the sum of three continuous functions satisfying 7\. The paper [3] is in a slightly different vein, in which an a.e. equivalent definition of n(y) is given with applications in Fourier series. For example (assuming/(0) =/(l)), the condition | log+ n(y)dy < °o is shown to imply the uniform convergence of the Fourier series of /<*)• The results quoted above are all applications of measure-theoretic arguments to the function n(y); the purpose of this paper is to look at implications of the topological properties of n(y). -

Flourish: Positive Psychology and Positive Interventions
Flourish: Positive Psychology and Positive Interventions MARTIN SELIGMAN T T L H V Delivered at e University of Michigan October , ¥ works on positive psychology, learned helplessness, depression, optimism, and pessimism. He is currently Zellerbach Family Professor of Psychology in the Department of Psychology at the Univer- sity of Pennsylvania and the director of the Positive Psychology Center. He was elected president of the American Psychological Association in by the largest vote in history. Dr. Seligman’s bibliography includes twenty-one books and more than articles. Among his better-known works are the best-selling Authentic Happiness (), Helplessness ( ), Learned Optimism ( ), What You Can Change and What You Can’t ( ), e Optimistic Child ( ), and Character Strengths and Virtues (, with Christopher Peterson). His books have been translated into more than thirty languages. His latest book is Flourish (). Dr. Seligman is the recipient of three Distinguished Scientic Contri- bution Awards from the American Psychological Association, the Laurel Award of the American Association for Applied Psychology and Preven- tion, the Lifetime Achievement Award of the Society for Research in Psychopathology, and the rst Wiley Psychology Lifetime Award of the British Academy. § § Á ¶ We have a strange heritage about the positive and negative sides of life. Our heritage comes from Schopenhauer and Freud who told us that the best we can ever hope for is to keep our misery and suering to a mini- mum. I want to suggest today the possibility of a positive human future. Until the possibility that there is more to life than minimizing suering gets on the radar screen, a positive human future is much less likely.