Combining Orthopedic Special Tests to Improve Diagnosis of Shoulder Pathology
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unicompartmental Knee Replacement
This is a repository copy of Unicompartmental Knee Replacement. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/120113/ Version: Accepted Version Article: Takahashi, T, Pandit, HG orcid.org/0000-0001-7392-8561 and Phil, D (2017) Unicompartmental Knee Replacement. Journal of Arthroscopy and Joint Surgery, 4 (2). pp. 55-60. ISSN 0021-8790 https://doi.org/10.1016/j.jajs.2017.08.009 © 2017 International Society for Knowledge for Surgeons on Arthroscopy and Arthroplasty. Published by Elsevier, a division of RELX India, Pvt. Ltd. This manuscript version is made available under the CC-BY-NC-ND 4.0 license http://creativecommons.org/licenses/by-nc-nd/4.0/ Reuse This article is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivs (CC BY-NC-ND) licence. This licence only allows you to download this work and share it with others as long as you credit the authors, but you can’t change the article in any way or use it commercially. More information and the full terms of the licence here: https://creativecommons.org/licenses/ Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ Accepted Manuscript Title: Unicompartmental Knee Replacement Author: Tsuneari Takahashi PII: S2214-9635(17)30041-X DOI: http://dx.doi.org/doi:10.1016/j.jajs.2017.08.009 Reference: JAJS 97 To appear in: Authors: Hemant G. -

Arthroscopy - Orthoinfo - AAOS 6/10/12 3:40 PM
Arthroscopy - OrthoInfo - AAOS 6/10/12 3:40 PM Copyright 2010 American Academy of Orthopaedic Surgeons Arthroscopy Arthroscopy is a surgical procedure orthopaedic surgeons use to visualize, diagnose, and treat problems inside a joint. The word arthroscopy comes from two Greek words, "arthro" (joint) and "skopein" (to look). The term literally means "to look within the joint." In an arthroscopic examination, an orthopaedic surgeon makes a small incision in the patient's skin and then inserts pencil-sized instruments that contain a small lens and lighting system to magnify and illuminate the structures inside the joint. Light is transmitted through fiber optics to the end of the arthroscope that is inserted into the joint. By attaching the arthroscope to a miniature television camera, the surgeon is able to see the interior of the joint through this very small incision rather than a large incision needed for surgery. The television camera attached to the arthroscope displays the image of the joint on a television screen, allowing the surgeon to look, for example, throughout the knee. This lets the surgeon see the cartilage, ligaments, and under the kneecap. The surgeon can determine the amount or type of injury and then repair Here are parts of the shoulder joint as or correct the problem, if it is necessary. seen trhough an arthroscope: the rotator cuff (RC), the head fo the humerus Why is arthroscopy necessary? (HH), and the biceps tendon (B). Diagnosing joint injuries and disease begins with a thorough medical history, physical examination, and usually X-rays. Additional tests such as magnetic resonance imaging (MRI) or computed tomography (CT) also scan may be needed. -

Download Program
38th Annual San Diego Course June 4 – 5, 2021 Interactive Virtual Shoulder Course Arthroscopy Arthroplasty Fractures Program Chairmen: James C. Esch, M.D., SDSI President and C.E.O. Patrick J. Denard, M.D., Program Chair Final Program Tornier. A trusted name. A relentless focus. Innovation Now driven by Stryker. We’re doubling down on shoulder arthroplasty and to a T. renewing our promise to you and the patients you serve. Stryker. The leader, committed to making healthcare better. Tornier. The shoulder solutions, driving industry-leading innovation. You. The surgeon, delivering better outcomes for your patients. Coming together is what sets us apart. The innovation continues Summer 2021. TM and ® denote Trademarks and Registered Trademarks of Stryker Corporation or its affiliates. ©2021 Stryker Corporation or its affiliates. AP-015176A 06-MAY-2021 Instability excellence Redefining peak performance Elevate your expertise for shoulder instability repairs. With solutions ranging from simple to complex, Smith+Nephew’s Instability Excellence portfolio is setting new standards to take you to the next level while returning your patients to peak performance. Learn more at smith-nephew.com. Smith & Nephew, Inc., 150 Minuteman Road, Andover, MA 01810, www.smith-nephew.com, T +978 749 1000, US Customer Service: +1 800 343 5717 ◊Trademark of Smith+Nephew. All trademarks acknowledged. ©2021 Smith+Nephew. All rights reserved. Printed in USA. 30280 V1 04/21 Advanced healing solutions Redefining healing potential for rotator cuff repair REGENESORB◊ Material Replaced by bone within 24 months.*1,2 at 6 months at at 18 months at Comparisons of absorption, measured via μCT, at 6 and 18 months.3 Suture Anchor Learn more at smith-nephew.com. -

The Benefit of Arthroscopy for Symptomatic Total Knee Arthroplasty
CORE Metadata, citation and similar papers at core.ac.uk Provided by Elsevier - Publisher Connector Arthroscopy for symptomatic total knee arthroplasty THE BENEFIT OF ARTHROSCOPY FOR SYMPTOMATIC TOTAL KNEE ARTHROPLASTY Hsiu-Peng Teng, Yi-Jiun Chou, Li-Chun Lin, and Chi-Yin Wong Department of Orthopedic Surgery, Kaohsiung Veterans General Hospital, Kaohsiung, Taiwan. Thirty-one knees with symptomatic total knee arthroplasty were diagnosed and treated arthroscopically. There were 18 knees with soft tissue impingement and 13 knees without. There were 16 knees with painful arthroplasty and range of motion (ROM) greater than 90°. Hypertrophied synovitis with or without impingement was more easily found by arthroscopy in this group than in the other 15 knees with the chief complaint of limited ROM, where more remarkable fibrotic tissue with intra-articular adhesion was found. Overall, the average improvement in ROM was 43.1° immediately after arthroscopy, and 20° at the final follow-up. Symptoms improved in 90.3% of patients, and 58.1% were satisfied with the outcome of their surgery. Arthroscopy is helpful for intra-articular diagnosis, obtaining a specimen for histopatho- logic analysis, culture for subclinical infection, and better improvement in ROM. In our experience, arthros- copy for symptomatic knee arthroplasty is reliable, safe and effective. Key Words: arthroscopy, total knee arthroplasty (Kaohsiung J Med Sci 2004;20:473–7) Total knee arthroplasty (TKA) is a popular and successful detailed history review, physical examination, and radio- treatment for knee-joint problems. However, a subset of graphic studies (anteroposterior, lateral and Merchant patients will suffer from persistent pain, with or without in- views) to detect possible pathologic conditions (e.g. -

Procedure Name: Knee Arthroscopy Brief Description of Procedure
Procedure Name: Knee Arthroscopy Brief Description of Procedure: Arthroscopic surgery is a common orthopedic procedure that is used to diagnose and treat problems in joints. Greek words: ‘arthro,’ meaning “joint” and ‘scope,’ meaning, “look.” When arthroscopy is per- formed, a telescope with a camera is inserted into the joint through a small incision. The camera is attached to a light source and shows a picture of the inside of the joint on a monitor. One or more incisions may be made to treat the underlying problem. This procedure can be used to diagnose a joint problem, perform surgery that repairs a joint problem, remove a loose or foreign body, or monitor a dis- ease or the effectiveness of a treatment. Arthroscopy is commonly performed on the knee, shoulder, and ankle. It also can be done on the hip, elbow, and wrist. Describe anesthesia type that typically is given: General Anesthesia is usually used for this surgery. See Anesthesia Section. What patients that smoke can expect when having surgery: After surgery your anesthesia specialist will check your breathing and lung sounds to determine if a breathing treatment is needed. Smoking increases airway irritation, which leads to wheezing and coughing. Further breathing treatments and medications are sometimes needed. Average length of surgery time: 45 minutes-1 hour Average length in immediate recovery: 30 minutes Average length for time of discharge: Expect to be here an average of one hour after surgery. During this time you may experience some discomfort. Medication can be given to make pain bearable. When can you go back to work: Depending on your occupation you and your doctor will discuss when you may return to work. -

Procedure Coding in ICD-9-CM and ICD- 10-PCS
Procedure Coding in ICD-9-CM and ICD- 10-PCS ICD-9-CM Volume 3 Procedures are classified in volume 3 of ICD-9-CM, and this section includes both an Alphabetic Index and a Tabular List. This volume follows the same format, organization and conventions as the classification of diseases in volumes 1 and 2. ICD-10-PCS ICD-10-PCS will replace volume 3 of ICD-9-CM. Unlike ICD-10-CM for diagnoses, which is similar in structure and format as the ICD-9-CM volumes 1 and 2, ICD-10-PCS is a completely different system. ICD-10-PCS has a multiaxial seven-character alphanumeric code structure providing unique codes for procedures. The table below gives a brief side-by-side comparison of ICD-9-CM and ICD-10-PCS. ICD-9-CM Volume3 ICD-10-PCS Follows ICD structure (designed for diagnosis Designed and developed to meet healthcare coding) needs for a procedure code system Codes available as a fixed or finite set in list form Codes constructed from flexible code components (values) using tables Codes are numeric Codes are alphanumeric Codes are 3-4 digits long All codes are seven characters long ICD-9-CM and ICD-10-PCS are used to code only hospital inpatient procedures. Hospital outpatient departments, other ambulatory facilities, and physician practices are required to use CPT and HCPCS to report procedures. ICD-9-CM Conventions in Volume 3 Code Also In volume 3, the phrase “code also” is a reminder to code additional procedures only when they have actually been performed. -
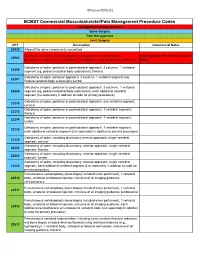
Commercial MSK Procedure Code List Effective 09.01.21.Xlsx
Effective 09/01/21 BCBST Commercial Musculoskeletal/Pain Management Procedure Codes Investigational or Non-Covered Spine Surgery Pain Management Joint Surgery CPT Description Commercial Notes 20930 Allograft for spine surgery only morselized Computer-assisted surgical navigational procedure for musculoskeletal Investigational Per BCBST Medical 20985 procedures, image-less (List separately in addition to code for primary procedure) Policy Osteotomy of spine, posterior or posterolateral approach, 3 columns, 1 vertebral 22206 segment (eg, pedicle/vertebral body subtraction); thoracic Osteotomy of spine, posterior approach, 3 columns, 1 vertebral segment (eg. 22207 Pedicle/vertebral body subtraction);lumbar Osteotomy of spine, posterior or posterolateral approach, 3 columns, 1 vertebral 22208 segment (eg, pedicle/vertebral body subtraction); each additional vertebral segment (list separately in addition to code for primary procedure) Osteotomy of spine, posterior or posterolateral approach, one vertebral segment; 22210 cervical Osteotomy of spine, posterior or posterolateral approach, 1 vertebral segment; 22212 thoracic Osteotomy of spine, posterior or posterolateral approach, 1 vertebral segment; 22214 lumbar Osteotomy of spine, posterior or posterolateral approach, 1 vertebral segment; 22216 each additional vertebral segment (List separately in addition to primary procedure) Osteotomy of spine, including discectomy anterior approach, single vertebral 22220 segment; cervical Osteotomy of spine, including discectomy, anterior approach, single -

Assessment of Discectomy and Eminectomy for Temporomandibular Joint Derangement: Manitoba Experience
Assessment of Discectomy and Eminectomy for Temporomandibular Joint Derangement: Manitoba Experience Bachelor of Science in Dentistry (B.Sc. Dent) Thesis By: Harmeet Manghera B.Sc. Dent 2019 Supervisors: Dr. Reda F. Elgazzar and Dr. Adnan Shah Dental Diagnostic and Surgical Sciences Oral and MaxilloFacial Surgery TABLE OF CONTENTS ACKNOWLEDGEMENTS …….……...…………………………………………………..….… 3 ABSTRACT …………………………………………………………………………………..…..4 INTRODUCTION …………………………………….………………………………………….5 PATIENTS AND METHODS………………………………………………...………………….7 RESULTS………………………………………………………………………..……………......9 DISCUSSION…………………………………………………………………………...……….13 CONCLUSION…………………………………………………………………….…………….17 REFERENCES…………………………………………………………………………………. 18 2 Acknowledgements I wish to express my sincere gratitude towards my mentors Dr. Elgazzar and Dr. Shah, in the department of DDSS/OMFS, for their encouragement and supervision during this project. I am also grateful to Dr. Bhullar, the Associate Dean of Research, for running the BSc (Dent) Program through the Faculty of Dentistry, University of Manitoba. This project was partially supported by the Canadian Association of Oral and Maxillofacial Surgeons. HSC and SOGH Health Records personnel provided the resources needed to complete this thesis. It would not have been possible without their help. I am thankful for my parents for providing moral support and encouragement along the journey. 3 Abstract Temporomandibular joint disorder (TMD) is caused by the loss of function of the intra- articular tissues, leading to a failure in the -

Minimally Invasive Orthopedic Surgery: Arthroscopy
Minimally Invasive Orthopedic Surgery: Arthroscopy Robert Treuting, MD Department of Surgery, Ochsner Clinic and Alton Ochsner Medical Foundation, New Orleans, LA Arthroscopy,aminimallyinvasivealternativetostandardopensurgicaltechniquesandnowthemostcommonly performedorthopedicsurgicalprocedure,wasoneofthegreatestadvancesinorthopedicsurgeryofthe20 th century.Minimallyinvasivesurgeriesresultinlesspostoperativeswellingthanopentechniquesandreduce pain,riskofcomplications,andrecoverytimes.Arthroscopyhasevolvedfromadiagnostictooltoatherapeutic toolcapableoftreatingawiderangeofinjuriesanddisorders.Manyinjuries,particularlythosethatatonetime wouldhavebeencareerendingforathletes,cannowbeaddressedwitharthroscopyallowingaquickerreturnto fullfunction.Whilearthroscopyhasresultedinanoveralldecreaseinmorbiditycomparedwithopentechniques, itisstillaninvasiveprocedureandinherentlyinvolvesrisks.Almostallarthroscopicprocedurescanbeperformed inanoutpatientsetting.In1999,211arthroscopicprocedureswereperformedatOchsner. TreutingR.Minimallyinvasiveorthopedicsurgery:arthroscopy.TheOchsnerJournal2000;2:158-163. rthopedicsurgery,likeallfieldsofmedicine,experienced outbreakofWorldWarII.In1921,Bircher(1882-1956)useda tremendousprogressinthe20thcentury.Alongwithan modifiedJacobaeuslaparoscopetovisualizetheinteriorofthe O improvedunderstandingofbasicmolecular,cellular, kneein18patientsinSwitzerlandandlaterpublishedhisfindings genetic,andbiomechanicalfactorsofthemusculoskeletalsystem, onposttraumaticarthritisandthediagnosisofmeniscalpathology jointreplacementsurgeryandarthroscopicsurgerywerethetwo -

See a Sample Opinion
Hospital for Special Surgery COMPREHENSIVE REPORT & CARE PLAN HSS REMOTE 2nd Opinion Rick Hannan | Dr. Danyal H. Nawabi Prepared on 08/11/2020 Dr. Danyal H. Nawabi About Dr. Nawabi Dr. Danyal H. Nawabi is an orthopedic surgeon in the Sports Medicine Institute. He is a specialist in the fields of knee, shoulder, and hip surgery, performing both arthroscopic surgery and joint replacement. Dr. Nawabi completed his medical training at Oxford University in England and residency in orthopedic surgery on the prestigious Percivall Pott Rotation in London, training at the Royal National Orthopaedic and the Royal London Hospitals. He was awarded the Sir Walter Mercer Gold Medal as the top graduating resident in the UK and served as the British Orthopaedic Association Young Ambassador in 2010. Following residency, he completed three years of advanced fellowship training in total joint replacement, sports medicine, and hip preservation at HSS, where he was a double recipient of the Philip D. Wilson Award for Excellence in Orthopaedic Surgery. Dr. Nawabi has special expertise in ACL reconstruction, sports knee 2 and shoulder injuries, hip arthroscopy and robotic-assisted joint replacement in young and active patients. His expertise in sports knee and shoulder surgery was developed in London after completing a dedicated one year fellowship under the supervision of the internationally renowned sports surgeon, Dr. Andy Williams. During this fellowship he gained experience treating elite soccer athletes from Chelsea Football Club and other English Premier League clubs. He has served as an assistant team physician to the New York Red Bulls MLS franchise. Dr. Nawabi’s expertise in hip surgery was developed at HSS during a one year fellowship under the supervision of Dr. -

Icd-9-Cm (2010)
ICD-9-CM (2010) PROCEDURE CODE LONG DESCRIPTION SHORT DESCRIPTION 0001 Therapeutic ultrasound of vessels of head and neck Ther ult head & neck ves 0002 Therapeutic ultrasound of heart Ther ultrasound of heart 0003 Therapeutic ultrasound of peripheral vascular vessels Ther ult peripheral ves 0009 Other therapeutic ultrasound Other therapeutic ultsnd 0010 Implantation of chemotherapeutic agent Implant chemothera agent 0011 Infusion of drotrecogin alfa (activated) Infus drotrecogin alfa 0012 Administration of inhaled nitric oxide Adm inhal nitric oxide 0013 Injection or infusion of nesiritide Inject/infus nesiritide 0014 Injection or infusion of oxazolidinone class of antibiotics Injection oxazolidinone 0015 High-dose infusion interleukin-2 [IL-2] High-dose infusion IL-2 0016 Pressurized treatment of venous bypass graft [conduit] with pharmaceutical substance Pressurized treat graft 0017 Infusion of vasopressor agent Infusion of vasopressor 0018 Infusion of immunosuppressive antibody therapy Infus immunosup antibody 0019 Disruption of blood brain barrier via infusion [BBBD] BBBD via infusion 0021 Intravascular imaging of extracranial cerebral vessels IVUS extracran cereb ves 0022 Intravascular imaging of intrathoracic vessels IVUS intrathoracic ves 0023 Intravascular imaging of peripheral vessels IVUS peripheral vessels 0024 Intravascular imaging of coronary vessels IVUS coronary vessels 0025 Intravascular imaging of renal vessels IVUS renal vessels 0028 Intravascular imaging, other specified vessel(s) Intravascul imaging NEC 0029 Intravascular -

Knee Replacement Surgery (Arthroplasty), Total and Partial
UnitedHealthcare® Commercial Medical Policy Surgery of the Knee Policy Number: 2021T0553S Effective Date: July 1, 2021 Instructions for Use Table of Contents Page Related Commercial Policy Coverage Rationale ........................................................................... 1 • Unicondylar Spacer Devices for Treatment of Pain Documentation Requirements......................................................... 1 or Disability Definitions ........................................................................................... 2 Community Plan Policy Applicable Codes .............................................................................. 2 • Surgery of the Knee U.S. Food and Drug Administration ................................................ 3 References ......................................................................................... 4 Medicare Advantage Coverage Summary Policy History/Revision Information................................................ 4 • Joints and Joint Procedures Instructions for Use ........................................................................... 5 Coverage Rationale Surgery of the Knee is proven and medically necessary in certain circumstances. For medical necessity clinical coverage criteria, refer to the InterQual® 2021, Apr. 2021 Release, CP: Procedures: • Arthroscopy, Diagnostic, +/- Synovial Biopsy, Knee • Arthroscopy or Arthroscopically Assisted Surgery, Knee • Arthrotomy, Knee • Total Joint Replacement (TJR), Knee • Removal and Replacement, Total Joint Replacement (TJR),