KINEMATIC MODELING of the TECHNIQUE STALDER BACKWARD to HANDSTAND on the UNEVEN BARS UDC 796.41:531.1 Emilija Petković
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Gymnastics Results
Olympic Indoor Hall Gymnastics Artistic Ολυµπιακό Κλειστό Γυµναστήριο Ενόργανη Γυµναστική / Gymnastique Artistique Gymnase Olympique Women’s Qualification Προκριµατικοί Γυναικών / Qualification Dames SUN 15 AUG 2004 Uneven Bars 21:00 Ασύµµετρο ∆ίζυγο / Barres asymétriques Results Αποτελέσµατα / Résultats RankBib Name NOC Total Code 1 392 KHORKINA Svetlana RUS 9.750 Q 2 334 LIN Li CHN 9.700 Q 3 333 LI Ya CHN 9.675 Q 4 354 LEPENNEC Emilie FRA 9.662 Q 5 414 KUPETS Courtney USA 9.637 Q 6 385 SOFRONIE N. ROM 9.625 Q 6 413 HUMPHREY Terin USA 9.625 Q 8 416 PATTERSON Carly USA 9.600 9 332 FAN Ye CHN 9.600 10 375 PYON Kwang Sun PRK 9.600 Q 11 415 MCCOOL Courtney USA 9.575 12 403 KRASNYNSKA Irina UKR 9.575 R 13 365 TWEDDLE Elizabeth GBR 9.575 R 14 313 HYPOLITO Daniele BRA 9.575 R 14 342 GENER Tania ESP 9.575 16 352 CHAOUCH Soraya FRA 9.550 17 371 HAN Jong Ok PRK 9.537 18 336 ZHANG Nan CHN 9.525 19 343 GOMEZ Elena ESP 9.525 20 335 WANG Tiantian CHN 9.512 21 353 DEBAUVE Marine FRA 9.500 22 410 BHARDWAJ Mohini USA 9.487 23 323 PLANTE Amelie CAN 9.475 24 391 EZHOVA Liudmila RUS 9.475 25 374 KIM Un Jong PRK 9.475 26 346 MORO Sara ESP 9.450 27 439 van LEEUWEN Laura NED 9.437 28 304 RUSSO Monette AUS 9.437 29 381 BAN Oana ROM 9.425 30 317 COMIN Camila BRA 9.412 31 305 SKINNER Lisa AUS 9.387 32 429 BISMPIKOU Stefani GRE 9.387 33 384 ROSU Monica ROM 9.375 34 345 MORENO Patricia ESP 9.375 35 315 RODRIGUES Ana Paula BRA 9.375 36 434 OSHIMA Kyoko JPN 9.362 37 302 MOORHOUSE Stephanie AUS 9.337 38 355 SCHMUTZ Camille FRA 9.337 39 386 STROESCU Silvia ROM 9.325 40 301 NGUYEN Karen AUS 9.300 41 382 EREMIA A. -

P020110307527551165137.Pdf
CONTENT 1.MESSAGE FROM DIRECTOR …………………………………………………………………………………………………………………………………………………… 03 2.ORGANIZATION STRUCTURE …………………………………………………………………………………………………………………………………………………… 05 3.HIGHLIGHTS OF ACHIEVEMENTS …………………………………………………………………………………………………………………………………………… 06 Coexistence of Conserve and Research----“The Germplasm Bank of Wild Species ” services biodiversity protection and socio-economic development ………………………………………………………………………………………………………………………………………………… 06 The Structure, Activity and New Drug Pre-Clinical Research of Monoterpene Indole Alkaloids ………………………………………… 09 Anti-Cancer Constituents in the Herb Medicine-Shengma (Cimicifuga L) ……………………………………………………………………………… 10 Floristic Study on the Seed Plants of Yaoshan Mountain in Northeast Yunnan …………………………………………………………………… 11 Higher Fungi Resources and Chemical Composition in Alpine and Sub-alpine Regions in Southwest China ……………………… 12 Research Progress on Natural Tobacco Mosaic Virus (TMV) Inhibitors…………………………………………………………………………………… 13 Predicting Global Change through Reconstruction Research of Paleoclimate………………………………………………………………………… 14 Chemical Composition of a traditional Chinese medicine-Swertia mileensis……………………………………………………………………………… 15 Mountain Ecosystem Research has Made New Progress ………………………………………………………………………………………………………… 16 Plant Cyclic Peptide has Made Important Progress ………………………………………………………………………………………………………………… 17 Progresses in Computational Chemistry Research ………………………………………………………………………………………………………………… 18 New Progress in the Total Synthesis of Natural Products ……………………………………………………………………………………………………… -

Entries WAG AARHUS 2006-AA
NOMINATIVE ENTRIES WOMEN'S ARTISTIC GYMNASTICS 39th Artistic Gymnastics World Championships AARHUS (DEN), 2006 Category Fed/Name Birth Yr All Around 50041 ARG DOMENEGHINI Nadir 1990 16 50044 ARG FICOSECCO Eugenia 1987 19 50042 ARG FRATANTUENO Agostina 1989 17 18058 ARG GONZALEZ Aylen 1989 17 17229 ARG POLIANDRI Sol 1988 18 50043 ARG POTOCHNIK Tatiana 1990 16 50072 AUS BONORA GEORGIA 1990 16 19316 AUS DYKES Hollie 1990 16 50071 AUS HERNANDEZ Melody 1990 16 19313 AUS JOURA Daria 1990 16 50132 AUS MORGAN Shona 1990 16 17555 AUS NGUYEN Karen 1987 19 18665 AUS VIVIAN Olivia 1989 17 16094 AUT HASENOEHRL Carina 1988 18 16095 AUT MAYER Sandra 1988 18 17068 BEL HENRY Chloé 1987 19 16890 BEL VANWALLEGHEM Aagje 1987 19 17079 BLR DMITRANITSA Liudmila 1989 17 18696 BLR LARINA Tatsiana 1989 17 17077 BLR MAKSHTAROVA Viktoria 1990 16 17075 BLR MARACHKOUSKAYA Nastassia 1990 16 13442 BLR NOVIKAVA Aksana 1987 19 50040 BLR SHAKOTS Volha 1990 16 16102 BLR SYCHEUSKAYA Alina 1988 18 50067 BRA CHAVES SANTOS Juliana 1990 16 13159 BRA COMIN Camila 1983 23 18053 BRA DA COSTA Bruna 1989 17 13160 BRA DOS SANTOS Daiane 1983 23 13161 BRA HYPOLITO Daniele 1984 22 16234 BRA SOUZA Lais 1988 18 17083 BUL GEORGIEVA Silvia 1990 16 16289 BUL HRISTOVA Veneta 1988 18 17080 BUL IOTOVA Suzana 1987 19 1097 BUL KARPENKO Victoria 1981 25 18543 BUL STANKOVA Mariana 1990 16 13386 BUL TANKOUCHEVA Nikolina 1986 20 *=Reserve gymnast Updated 29.09.2006 15:02:28 Page 1/7 NOMINATIVE ENTRIES WOMEN'S ARTISTIC GYMNASTICS 39th Artistic Gymnastics World Championships AARHUS (DEN), 2006 Category -

2017 – 2020 CODE of POINTS Women's Artistic Gymnastics
FÉDÉRATION INTERNATIONALE DE GYMNASTIQUE 2017 – 2020 CODE OF POINTS Women’s Artistic Gymnastics Approved by the FIG Executive Committee For Women’s Artistic Gymnastics competitions at Olympic Games Youth Olympic Games World Championships Regional and Intercontinental Competitions Events with international participants In competitions for nations with lower level of gymnastics development, as well as for Junior Competitions, modified competition rules should be appropriately designed by continental or regional technical authorities, as indicated by the age and level of development (see the FIG Age Group Development Program) The Code of Points is the property of the FIG. Translation and copying are prohibited without prior written approval by FIG. In case any statement contained herein is in conflict with the Technical Regulations, the Technical Regulations shall take precedence. Where there is a difference among the languages, the English text shall be considered correct. ii ACKNOWLEDGEMENTS FIG CODE UPDATES President Nellie Kim BLR After the Official FIG Competitions the FIG/WTC publishes a WAG 1st Vice-President Donatella Sacchi ITA Newsletter which includes: 2nd Vice-President Naomi Valenzo MEX – all new elements and variations with a number and illustration Secretary Kym Dowdell AUS – new connections Member Qiurui Zhou CHN Member Yoshie Harinishi JPN The Code Update will be sent by the FIG Secretary General to all affiliated Member Loubov Burda-Andrianova RUS federations, including the effective date, from which time it is valid for all Athlete representative Beth Tweddle GBR further FIG competitions. James Stephenson & USA Illustrations Koichi Endo JPN Original illustrations Ingrid Nicklaus GER HELP DESK Original Symbols Margot Dietz GER For additional examples, descriptions, definitions, updates and clarifications can be found at the FIG website under WAG Help Desk. -

12Th ARTISTIC GYMNASTICS WORLD-CUP FINAL NIA, Birmingham
12th ARTISTIC GYMNASTICS WORLD-CUP FINAL NIA, Birmingham (GBR) 11 - 12 December 2004 INDIVIDUAL JUDGES SCORES Women’s Seniors - Apparatus Finals SUN 12 DEC 2004 - 13:09 NOC B1 B2 B3 B4 B5 B6 RankBib Name SV Pen. Total Code FIG FIG FIG MEX CZE ARG 1 65 PONOR Catalina ROM 10.00 9.75 9.65 9.70 9.75 9.75 9.70 9.725 2 54 LI Ya CHN 10.00 9.55 9.70 9.60 9.70 9.60 9.55 9.612 3 64 EREMIA A. ROM 10.00 9.60 9.70 9.60 9.60 9.60 9.65 9.612 4 57 ZHANG Nan CHN 10.00 9.60 9.70 9.45 9.55 9.65 9.60 9.600 5 67 EZHOVA Liudmila RUS 10.00 9.35 9.60 9.45 9.40 9.50 9.40 9.437 6 53 FAN Ye CHN 9.80 9.20 9.20 8.95 9.15 9.25 9.15 9.175 7 51 HYPOLITO Daniele BRA 9.90 9.05 8.80 9.00 9.00 8.95 8.80 8.937 8 68 PAVLOVA Anna RUS 9.80 8.80 8.90 8.90 8.60 8.80 8.90 8.850 Legend SV Start value B1 - B6 Panel "B" judges 1 - 6 Pen Penalty Beam GAW008101_75C 1.0 Report Created SUN 12 DEC 2004 13:33 Page 1/1 12th ARTISTIC GYMNASTICS WORLD-CUP FINAL NIA, Birmingham (GBR) 11 - 12 December 2004 INDIVIDUAL JUDGES SCORES Women’s Seniors - Apparatus Finals SUN 12 DEC 2004 - 14:14 NOC B1 B2 B3 B4 B5 B6 RankBib Name SV Pen. -

39TH ARTISTIC GYMNASTICS WORLD CHAMPIONSHIPS Aarhus (DEN) October 13Th
39TH ARTISTIC GYMNASTICS WORLD CHAMPIONSHIPS Aarhus (DEN) October 13th - 21st 2006 Results Women’s Individual All-Around Final THU 19 OCT 2006 - 19:30 NOC RankBib Name Total Code 1363 FERRARI VanessaITA 14.800 15.825 14.900 15.500 61.025 2391 BIEGER Jana USA 14.725 15.350 15.300 15.375 60.750 3472 IZBASA Sandra RalucaROM 15.025 14.225 15.475 15.525 60.250 4474 NISTOR Steliana ROM 14.275 15.275 15.800 14.600 59.950 5113 JOURA Daria AUS 14.500 15.100 15.000 15.275 59.875 6194 PANG Panpan CHN 14.025 15.425 14.800 15.425 59.675 7111 DYKES Hollie AUS 14.350 14.975 15.625 14.550 59.500 8294 TWEDDLE ElizabethGBR 14.550 14.700 14.950 15.250 59.450 9303 CHUSOVITINA OksanaGER 15.000 14.700 14.375 14.875 58.950 10396 PRIESS Ashley USA 14.450 15.425 15.325 13.600 58.800 11285 SEVERINO IsabelleFRA 14.600 14.100 14.925 15.000 58.625 12196 ZHOU Zhuoru CHN 14.300 15.150 14.425 14.700 58.575 13403 KOZICH Alina UKR 14.500 13.875 15.175 14.650 58.200 14250 CAMPOS Laura ESP 14.825 14.550 14.575 14.150 58.100 15371 KURODA Mayu JPN 13.400 15.550 15.100 13.925 57.975 16174 HOPFNER-HIBBS ElyseCAN 13.950 14.325 15.125 14.300 57.700 16251 DE SIMONE LenikaESP 13.725 14.900 14.650 14.425 57.700 18495 KAESLIN Ariella SUI 13.575 14.675 15.075 14.350 57.675 19486 PAVLOVA Anna RUS 14.925 13.900 14.225 14.575 57.625 20281 LINDOR KatheleenFRA 14.450 14.125 14.725 14.300 57.600 21154 HYPOLITO DanieleBRA 13.750 14.150 14.575 14.700 57.175 22408 ZGOBA Dariya UKR 13.650 15.600 14.075 13.600 56.925 23451 HONG Su Jong PRK 15.700 13.350 13.275 13.750 56.075 24487 PRAVDINA KristinaRUS 13.675 13.275 14.850 13.725 55.525 Legend Vault Uneven Bars Beam Floor Note: Underlined totals indicate starting apparatus. -

ENTRY LIST by NOC WOMEN’S As of FRI 22 AUG 2003
37TH WORLD CHAMPIONSHIPS ARTISTIC GYMNASTICS Anaheim, California USA August 16-24, 2003 ENTRY LIST BY NOC WOMEN’S As of FRI 22 AUG 2003 NOC NOC Code NameBib Date of Birth ARG Argentina CARNEVALE Celeste Andrea101 25 AUG 1985 CONDE Maria Daniela102 26 NOV 1985 PARIGI Gabriela103 24 DEC 1985 SIROLLI Melina Debora104 23 APR 1984 STANCATO Cecilia Marianela105 14 OCT 1987 VASTA Ruth Belen106 18 SEP 1987 AUS Australia ARCHER Belinda109 6 FEB 1987 DUNN Jacqui110 5 MAR 1984 KELLY Danielle108 24 MAY 1986 MOORHOUSE Stephanie111 20 JAN 1987 RUSSO Monette112 4 AUG 1988 SKINNER Lisa113 17 FEB 1981 SLATER Allana114 3 APR 1984 AUT Austria AIGNER Julia116 4 JUL 1986 GRATT Tanja118 13 DEC 1986 HASENOEHRL Carina119 4 FEB 1988 MATZENAUER Nausikaa117 9 NOV 1986 MAYER Sandra120 24 SEP 1988 PRAXMARER Stefanie121 12 MAR 1987 BEL Belgium DEBRAS Caroline123 12 MAY 1978 SOHET Celine124 19 MAY 1985 VAN WALLEGHEM Aagje125 24 OCT 1987 BER Bermuda ASTWOOD Kalena127 5 NOV 1988 LOPES Casey128 27 SEP 1988 BLR Belarus MILKO Irina131 15 OCT 1986 NOVIKAVA Aksana132 24 MAR 1987 SIRUTZ Irina133 3 SEP 1988 SYCHEUSKAYA Alina130 9 DEC 1988 TARASENKA Yulia134 14 APR 1985 TIARENTIAVA Velha135 1 MAY 1988 ZHARGANOVA Tatiana136 24 JUL 1980 BOL Bolivia DE LA FUENTE PARADA Maria Jose138 2 DEC 1988 GA0000101_32A 1.0 Report Created FRI 22 AUG 2003 15:09 Page 1/19 37TH WORLD CHAMPIONSHIPS ARTISTIC GYMNASTICS Anaheim, California USA August 16-24, 2003 ENTRY LIST BY NOC WOMEN’S As of FRI 22 AUG 2003 NOC NOC Code NameBib Date of Birth BRA Brazil COMIN Camila141 31 MAR 1983 DOS SANTOS Daiane142 -

Vertical Facility List
Facility List The Walt Disney Company is committed to fostering safe, inclusive and respectful workplaces wherever Disney-branded products are manufactured. Numerous measures in support of this commitment are in place, including increased transparency. To that end, we have published this list of the roughly 7,600 facilities in over 70 countries that manufacture Disney-branded products sold, distributed or used in our own retail businesses such as The Disney Stores and Theme Parks, as well as those used in our internal operations. Our goal in releasing this information is to foster collaboration with industry peers, governments, non- governmental organizations and others interested in improving working conditions. Under our International Labor Standards (ILS) Program, facilities that manufacture products or components incorporating Disney intellectual properties must be declared to Disney and receive prior authorization to manufacture. The list below includes the names and addresses of facilities disclosed to us by vendors under the requirements of Disney’s ILS Program for our vertical business, which includes our own retail businesses and internal operations. The list does not include the facilities used only by licensees of The Walt Disney Company or its affiliates that source, manufacture and sell consumer products by and through independent entities. Disney’s vertical business comprises a wide range of product categories including apparel, toys, electronics, food, home goods, personal care, books and others. As a result, the number of facilities involved in the production of Disney-branded products may be larger than for companies that operate in only one or a limited number of product categories. In addition, because we require vendors to disclose any facility where Disney intellectual property is present as part of the manufacturing process, the list includes facilities that may extend beyond finished goods manufacturers or final assembly locations. -

APPARATUS NAMED AFTER FED DESCRIPTION EVENT / YEAR VIDEO Vault WOMEN's ARTISTIC GYMNASTICS ELEMENTS
WOMEN'S ARTISTIC GYMNASTICS ELEMENTS EVENT / APPARATUS NAMED AFTER FED DESCRIPTION VIDEO YEAR Vault Vault 1 Kim Nellie USSR Handspring fwd on - 1½ (540°) off WC Varna (BUL) 1974 Vault 1 Korbut Olga USSR Handspring fwd with 1/1 turn (360°) on - 1/1 turn (360°) off Vault 2 Chusovitina Oksana UZB Handspring fwd on - piked salto fwd with 1/1 turn (360°) off Vault 2 Chusovitina Oksana UZB Handspring fwd on - stretched salto fwd with 1½ turn (540°) off Vault 2 Davydova Elena USSR Handspring fwd with 1/1 turn (360°) on - tucked salto fwd off Vault 2 Evdokimova Irina KAZ Handspring fwd on - stretched salto fwd off Vault 2 Produnova Elena RUS Handspring fwd on - tucked double salto fwd off Vault 2 Wang Huiying CHN Handspring fwd on - stretched salto fwd with ½ turn (180°) off Vault 2 Yeo Seojeong KOR Handspring fwd on - stretched salto fwd with 2/1 turn (720°) off Korean Cup ( KOR) 2019 Vault 3 Kim Nellie USSR Tsukahara tucked with 1/1 turn (360°) off OG Montreal (CAN) 1976 Vault 3 Kim Nellie USSR Tsukahara stretched with 1/1 turn (360°) off WC Strasbourg (FRA) 1978 Vault 3 Tourischeva Liudmila USSR Tsukahara tucked Vault 3 Zamolodchikova Elena RUS Tsukahara stretched with 2/1 turn (720°) off Vault 4 Amanar Simona ROU Round-off flic-flac on - stretched salto bwd with 2½ turn (900°) off Vault 4 Dungelova Erika BUL Round-off flic-flac on - tucked salto bwd with 2/1 turn (720°) off Vault 4 Luconi Patrizia ITA Round-off, flic-flac with ¾ turn (270°) on – tucked salto bwd off Vault 4 Baitova Svetlana USSR Round-off flic-flac on - stretched salto bwd -
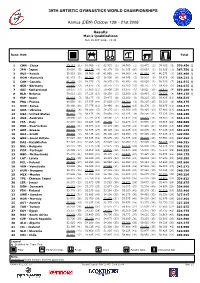
Qualification Team Results
39TH ARTISTIC GYMNASTICS WORLD CHAMPIONSHIPS Aarhus (DEN) October 13th - 21st 2006 Results Men’s Qualifications SUN 15 OCT 2006 - 19:30 Rank NOC Total 1 CHN - China 59.125 (11) 62.000 (1) 62.925 (2) 64.900 (1) 62.475 (2) 59.025 (8) 370.450 Q 2 JPN - Japan 59.650 (8) 59.275 (4) 62.175 (3) 61.975 (20) 63.050 (1) 61.625 (1) 367.750 Q 3 RUS - Russia 59.525 (10) 58.800 (6) 61.650 (4) 64.000 (4) 61.050 (4) 60.375 (2) 365.400 Q 4 ROM - Romania 61.475 (1) 60.200 (2) 59.800 (6) 64.075 (3) 59.900 (9) 58.875 (9) 364.325 Q 5 CAN - Canada 61.250 (2) 58.775 (7) 58.375 (15) 63.650 (6) 60.825 (6) 59.100 (7) 361.975 Q 6 GER - Germany 58.900 (13) 59.675 (3) 59.175 (12) 63.100 (10) 60.775 (7) 59.450 (5) 361.075 Q 7 SUI - Switzerland 59.675 (7) 57.950 (11) 59.400 (10) 63.675 (5) 59.625 (10) 58.875 (9) 359.200 Q 8 BLR - Belarus 58.625 (15) 57.125 (17) 60.150 (5) 62.800 (13) 60.950 (5) 59.525 (4) 359.175 Q 9 ESP - Spain 61.025 (3) 58.175 (9) 59.475 (8) 63.200 (9) 58.225 (15) 58.425 (12) 358.525 10 FRA - France 60.850 (5) 57.575 (14) 57.925 (17) 64.700 (2) 58.225 (15) 59.200 (6) 358.475 11 KOR - Korea 58.100 (18) 57.775 (12) 59.450 (9) 62.200 (18) 62.275 (3) 58.675 (11) 358.475 12 UKR - Ukraine 60.325 (6) 59.200 (5) 59.275 (11) 62.550 (15) 59.125 (13) 57.800 (14) 358.275 13 USA - United States 61.025 (3) 58.475 (8) 59.050 (14) 63.225 (8) 59.200 (11) 57.125 (20) 358.100 14 AUS - Australia 59.000 (12) 57.725 (13) 59.500 (7) 61.875 (23) 58.475 (14) 59.600 (3) 356.175 15 ITA - Italy 57.275 (22) 55.225 (23) 63.100 (1) 62.275 (17) 57.975 (17) 56.650 (22) 352.500 -

Gymnastic Artistic
Olympic Indoor Hall Gymnastics Artistic Ολυµπιακό Κλειστό Γυµναστήριο Ενόργανη Γυµναστική / Gymnastique Artistique Gymnase Olympique Competition Schedule Αγωνιστικό Πρόγραµµα / Horaire des Compétitions As of MON 16 AUG 2004 Date Time Event SAT 14 AUG Men’s Qualification 12:30 - Subdivision 1 16:30 - Subdivision 2 20:30 - Subdivision 3 SUN 15 AUG Women’s Qualification 10:00 - Subdivision 1 13:30 - Subdivision 2 17:00 - Subdivision 3 21:00 - Subdivision 4 MON 16 AUG 20:30 Men’s Team Final TUE 17 AUG 21:00 Women’s Team Final WED 18 AUG 20:30 Men’s All-Around Final THU 19 AUG 21:00 Women’s All-Around Final SUN 22 AUG Apparatus Finals - Day 1 20:00 - Men s Floor 20:35 - Women s Vault 21:08 - Men s Pommel Horse 21:43 - Women s Uneven Bars 22:14 - Men s Rings MON 23 AUG Apparatus Finals - Day 2 20:00 - Men s Vault 20:35 - Women s Beam 21:10 - Men s Parallel Bars 21:45 - Women s Floor 22:20 - Men s Horizontal Bar TUE 24 AUG 12:00 Gala Changed the day of the week for the gala. GA0000000_08 1.1 Report Created MON 16 AUG 2004 15:51 Page 1/1 Olympic Indoor Hall Gymnastics Artistic Ολυµπιακό Κλειστό Γυµναστήριο Ενόργανη Γυµναστική / Gymnastique Artistique Gymnase Olympique WOMEN’S Γυναικών / FEMMES Entry List by NOC Κατάλογος Συµµετεχόντων ανά ΕΟΕ / Liste des Participants par Pays As of SAT 14 AUG 2004 NOC NOC Code NameBib Date of Birth ARG Argentina CARNEVALE Celeste440 25 AUG 1985 AUS Australia MOORHOUSE Stephanie302 20 JAN 1987 MUNRO Melissa303 8 FEB 1988 NGUYEN Karen301 24 NOV 1987 RUSSO Monette304 4 AUG 1988 SKINNER Lisa305 17 FEB 1981 SLATER -

Powertech 2013 Poster Sessions
Monday 17h40 – 18h30 Makalu POSTER PRESENTATION A5619SA Advanced Combined Cycle Modeling Ammari S. (ALSTOM GRID, France), Cheung K.W. (ALSTOM GRID, United States) A5701JA Multinodal Load Forecasting Using an ART-ARTMAP-Fuzzy Neural Network and PSO Strategy Antunes J.F. (INSTITUTO FEDERAL DE EDUCAÇÃO - IFMT, Brazil), de Souza Araújo N.V. (UFMT, Brazil), Minussi C.R. (UNESP - UNIVERSIDADE ESTADUAL PAULISTA, Brazil) A5201BA A Novel Maximum Power Point Tracking for Photovoltaic Systems Axelrod B. (HOLON INSTITUTE OF TECHNOLOGY, Israel), Berkovich Y. (HOLON INSTITUTE OF TECHNOLOGY, Israel), Golan G. (HOLON INSTITUTE OF TECHNOLOGY, Israel) A6023FB Locating and Capacity Determination of Distributed Generations Using NSGA-II Algorithm Banihashemi F. (UNIVERSITY OF TEHRAN, Iran), Lesani H. (UNIVERSITY OF TEHRAN, Iran), Salar Makhzani A. (MULTIMEDIA UNIVERSITY CYBERJAYA, Malaysia) A5693BB Regime-based control to reduce power fluctuations from offshore wind power plants Barahona B. (TECHNICAL UNIVERSITY OF DENMARK, Denmark), Cutululis N.A. (TECHNICAL UNIVERSITY OF DENMARK, Denmark), Trombe P.-J. (TECHNICAL UNIVERSITY OF DENMARK, Denmark), Pinson P. (TECHNICAL UNIVERSITY OF DENMARK, Denmark) A5950SB A Control Method using PI/Fuzzy Controllers Based DFIG in Wind Energy Conversion System Louarem S. (UNIVERSITÉ SÉTIF I, Algeria), Belkhiat S. (UNIVERSITÉ SÉTIF I, Algeria), Chouaib Belkhiat D. E. (UNIVERSITE JOSEPH FOURIER, France) A5546XC A Service Restoration Algorithm Based on Subsystem-Switch for Power Grid Zhang X. (NORTH CHINA ELECTRIC POWER UNIVERSITY, China), Cheng X. (NORTH CHINA ELECTRIC POWER UNIVERSITY, China), Zhao D. (NORTH CHINA ELECTRIC POWER UNIVERSITY, China), Liu Y. (NORTH CHINA ELECTRIC POWER UNIVERSITY, China) A5955VD Five forecasting algorithms for energy consumption in Vietnam Tran V. G. (G2ELAB - GRENOBLE INSTITUTE OF TECHNOLOGY, France), Debusschère V.