DOCSLIB.ORG

Spectroscopy of Binaries in Globular Clusters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spectroscopy of Binaries in Globular Clusters Spectroscopy of Binaries in Globular Clusters Dissertation for the award of the degree “Doctor rerum naturalium” (Dr.rer.nat.) of the Georg-August-Universität Göttingen within the doctoral program PROPHYS of the Georg-August University School of Science (GAUSS) submitted by Benjamin David Giesers from Oldenburg Göttingen, 2019 Thesis Commitee Prof. Dr. Stefan Dreizler Sonnenphysik und Stellare Astrophysik, Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Dr. Sebastian Kamann Star formation and stellar populations, Astrophysics Research Institute, Liverpool John Moores University, United Kingdom Dr. Tim-Oliver Husser Stellare Astrophysik, Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Members of the Examination Board Reviewer: Prof. Dr. Stefan Dreizler Sonnenphysik und Stellare Astrophysik, Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Second Reviewer: Prof. Dr. Ulrich Heber Stellare Astrophysik, Dr. Karl Remeis Sternwarte, Friedrich-Alexander-Universität Erlangen- Nürnberg, Germany Further members of the Examination Board: Dr. Saskia Hekker Stellar Ages and Galactic Evolution, Max-Planck-Institut für Sonnensystemforschung, Göttin- gen, Germany Prof. Dr. Wolfram Kollatschny Extragalaktische Astrophysik, Institut für Astrophysik, Georg-August-Universität Göttingen, Germany Prof. Dr. Wolfgang Glatzel Sonnenphysik und Stellare Astrophysik, Institut für Astrophysik, Georg-August-Universität Göttingen, Germany PD Dr. Jörn Große-Knetter Kern- und Atomphysik, II. Physikalisches Institut, Georg-August-Universität Göttingen, Ger- many Date of the oral examination: 13 December 2019 Abstract The natural constants in the universe are adjusted so that dense and massive star forming re- gions can end up in gravitational bound star clusters, called globular clusters. These objects are found in all galaxies and are building blocks of galaxies and the universe. The kinematic properties of globular clusters cannot be explained by that of a population consisting only of single stars. In fact, an important aspect of these clusters are binary star systems, as they alter the dynamical evolution. To date, there are some estimates of the binary fraction of Galactic globular clusters, but very little is known about the properties of binary systems themselves. With their high mass, black holes can also have an important impact on the cluster evolution. However, black holes are extremely difficult to detect unless they are actively accreting. In order to gain insights into the binary properties, such as orbital period, multi-epoch spec- troscopic observations of individual stars in a given cluster are generally needed. However, classical spectrographs only offer limited capabilities when it comes to probing the crowded central regions of globular clusters where most of the binary systems are expected to be found. This is where the Multi Unit Spectroscopic Explorer (MUSE), a second generation instrument mounted on one of the Very Large Telescopes (VLTs), comes into play. With MUSE, the spectro- scopy of individual stars in cluster cores became not only feasible, but also observationally effi- cient. This work makes use of multi-epoch MUSE observations of 27 Galactic globular clusters, including more than 380 000 stars and 1 400 000 individual spectra, to derive radial velocities that allow the identification and characterisation of binary systems. For the first time in astronomy, three binary systems, each composed of a black hole and a visible stellar companion, were discovered by this blind spectroscopic survey. A fit of a Kep- lerian orbit to these systems allowed us to infer the properties which are accessible by the radial velocity method. These findings helped to understand the retention fraction of black holes and how they affect the dynamical properties of globular clusters. The identification of these three black holes in NGC 3201 provided evidence that the cluster hosts an extensive subsystem of black holes including at least 40 objects. Black holes, as well as the binary systems, provide the cluster with an extra source of energy that explains why the core of NGC 3201 is not as dense as expected for a 12 Gyr old simple stellar population. The pilot study on the globular cluster NGC 3201 shows what can be learned about the binary content of a globular cluster when using state-of-the-art observations and simulations. A new statistical method was developed to infer the binary probability of individual stars based on noisy and sparse radial velocities taking data from all stars of a given cluster into account. With the help of a sophisticated MOCCA globular cluster model of NGC 3201, the total binary fraction of 6:8 %, freed from many observational biases, was derived for this cluster. This is the most accurate estimate obtained to date. The best fitting MOCCA model also suggests that NGC 3201 was born with a large binary fraction (≥ 50 %) and that the present day binary population consists mainly of primordial binaries. For the first time in a study of globular clusters, Keplerian orbits to a significant sample of 95 binaries were obtained. The periods, eccentricities, and derived minimum companion masses of these systems give insights into the binary population of NGC 3201. The combination of Hubble Space Telescope (HST) photometry and literature data with the MUSE star sample of NGC 3201 revealed the binary nature and spectral properties of peculiar objects such as blue straggler stars, sub-subgiants, and eclipsing binaries. This showed a high blue straggler binary fraction of at least 58 % and evidence for two iii blue straggler formation scenarios in NGC 3201. On the one hand, blue stragglers are formed involving mass transfer in a binary or triple star system. On the other hand, blue stragglers are formed by the coalescence of two stars following the encounter of two binary systems. It is now known that most Galactic globular clusters do not consist of only one primordial stellar population, but have instead multiple populations that differ, for example, in elemental abundances. NGC 3201 shows two distinct populations and it was a logical step to compare the binary contents of these populations with each other. We found, that the binary fraction of the first population is significantly higher than the fraction of the second population. Previous studies have shown similar results for the outer regions of other clusters, but this work was the first to find such results in a cluster centre. This challenges some theories that expect the binary fractions of different populations in cluster centres to be the same. In the core of NGC 3201 the most plausible explanation is that the populations were formed with different primordial binary fractions, which is conceivable if the second population has been formed within and after the already formed first population. iv Acknowledgments I would like to thank Stefan Dreizler very much for enabling me to explore the different aspects of astrophysics. He is responsible for the multitude of opportunities I had during my Bachelor, Master, and PhD projects. I also give special thanks to my additional supervisors Sebastian Kamann and Tim-Oliver Husser, not only for their helpful and patient support, but for all the work done beforehand, without which this work would not have been possible. The opportunities allowed me to collaborate internationally with Guillem Anglada Escudé and Abbas Askar. Both have greatly contributed to the significance of my scientific work. I would like to thank the MUSE consortium for building such a wonderful instrument and organising several inspiring meetings all over Europe with many helpful scientific discussions. I also like to thank ESO for the preparation of the press release (especially Richard Hook) and the unique experience at the Paranal Observatory, which I will never forget. A special thanks goes to the co-authors of my papers, Abbas Askar, Guillem Anglada Es- cudé, Jarle Brinchmann, Peter Weilbacher, Marcella Carollo, Martin Roth, Martin Wendt, Lutz Wisotzki, Nate Bastian, Fabian Göttgens, Marilyn Latour, Tim-Oliver Husser, Sebastian Kamann, and Stefan Dreizler. Finally, I would like to thank a selection of people who have accompanied me on my scientific journey: Jantje Freudenthal, Marvin Böhm, Wolfram Kollatschny, Roland Bacon, Rick Hessman, Arash Bahramian, Robert Mathieu, and Stan Lai. Göttingen, October 2019 Benjamin Giesers v Contents 1. Introduction 1 1.1. Globular clusters . .2 1.1.1. Cluster formation . .4 1.1.2. Cluster evolution . .4 1.1.3. Binaries . .6 1.1.4. Blue stragglers . 10 1.1.5. Black holes . 12 1.1.6. Multiple populations . 14 1.1.7. Simulations . 16 1.2. Multiple star systems and binaries . 17 1.2.1. Observational techniques . 18 1.2.2. The radial velocity technique of binary systems . 19 1.3. Integral-field spectroscopy and MUSE . 21 1.4. MUSE survey of globular clusters . 22 1.4.1. Pilot study . 22 1.4.2. A stellar census of globular clusters with MUSE . 23 1.5. Aims of this work . 26 2. Publications 29 B. Giesers, S. Dreizler, T.-O. Husser, S. Kamann, G. Anglada Escudé, J. Brinchmann, C. M. Carollo, M. M. Roth, P. M. Weilbacher, and L. Wisotzki. A detached stellar- mass black hole candidate in the globular cluster NGC 3201. In Monthly Notices of the Royal Astronomical Society, volume 475, pages L15-L19, March 2018. 31 B. Giesers, S. Kamann, S. Dreizler, T.-O. Husser, A. Askar, F. Göttgens, J. Brinchmann, M. Latour, P. M. Weilbacher, M. Wendt, and M. M. Roth. A stellar census in globular clusters with MUSE: Binaries in NGC 3201. In Astronomy & Astrophysics, volume 632, pages A3, December 2019. 37 S. Kamann, B. Giesers., N. Bastian, J. Brinchmann, S. Dreizler, F. Göttgens, T.-O. Husser, M. Latour, P. M. Weilbacher, and L. Wisotzki. The binary content of multiple popula- tions in NGC 3201. In Astronomy & Astrophysics, volume 635, pages A65, March 2020. 57 3. Conclusions & Outlook 63 3.1. A new statistical method . 63 vii Contents 3.2. The binary fraction of NGC 3201 . 64 3.3. Orbital parameters of 95 binaries . 64 3.4.
Load more

Recommended publications
  • The Discovery of Exoplanets
    L'Univers, S´eminairePoincar´eXX (2015) 113 { 137 S´eminairePoincar´e New Worlds Ahead: The Discovery of Exoplanets Arnaud Cassan Universit´ePierre et Marie Curie Institut d'Astrophysique de Paris 98bis boulevard Arago 75014 Paris, France Abstract. Exoplanets are planets orbiting stars other than the Sun. In 1995, the discovery of the first exoplanet orbiting a solar-type star paved the way to an exoplanet detection rush, which revealed an astonishing diversity of possible worlds. These detections led us to completely renew planet formation and evolu- tion theories. Several detection techniques have revealed a wealth of surprising properties characterizing exoplanets that are not found in our own planetary system. After two decades of exoplanet search, these new worlds are found to be ubiquitous throughout the Milky Way. A positive sign that life has developed elsewhere than on Earth? 1 The Solar system paradigm: the end of certainties Looking at the Solar system, striking facts appear clearly: all seven planets orbit in the same plane (the ecliptic), all have almost circular orbits, the Sun rotation is perpendicular to this plane, and the direction of the Sun rotation is the same as the planets revolution around the Sun. These observations gave birth to the Solar nebula theory, which was proposed by Kant and Laplace more that two hundred years ago, but, although correct, it has been for decades the subject of many debates. In this theory, the Solar system was formed by the collapse of an approximately spheric giant interstellar cloud of gas and dust, which eventually flattened in the plane perpendicular to its initial rotation axis.
    [Show full text]
  • Globular Clusters by Steve Gottlieb
    Southern Globulars 6/27/04 9:19 PM Nebula Filters by Andover Ngc 60 Telestar NCG-60 $148 Meade NGC60 For viewing emission and Find, compare and buy 60mm Computer Guided Refractor Telescope $181 planetary nebulae. Telescopes! Simply Fast Telescope! Includes 4 eye Free Shipping. Affiliate. Narrowband and O-III types Savings www.amazon.com pieces - Affiliate www.andcorp.com www.Shopping.com www.walmart.com Observing Down Under: Part I - Globular Clusters by Steve Gottlieb Omega Centauri - HST This is the first part in a series based on my trip to Australia last summer, covering observations of a few southern showpiece objects. The other parts in the series are: Southern Planetaries Southern Galaxies Two Southern Galaxy Groups These observing notes were made in early July while my family was staying at the Magellan Observatory (astronomical farmstead) for eight nights. The observatory is in the southern tablelands of New South Wales between Goulburn and Canberra (roughly 3.5 hrs from Sydney) and is hosted by Zane Hammond and his wife Fiona. Viewing the showpiece southern globulars was high on my observing priorities for Australia. Because the center of the Milky Way wheels overhead from -35° latitude, the globular system is much better placed and several of the best globulars in the sky which are completely inaccessible from the north are well placed. In the August issue of S&T, Les Dalrymple (who I observed with one evening), ranked M13 no better than 8th among the best globulars visible from Australia. I'd still jack up its ranking a couple of notches, but it's just one of the weak runnerups to 47 Tucana and Omega Centauri viewed over 75° up in the sky and behind NGC 6752, 6397 and M22.
    [Show full text]
  • An Intriguing Globular Cluster in the Galactic Bulge from the VVV Survey ? D
    Astronomy & Astrophysics manuscript no. minni48_vf5 ©ESO 2021 June 29, 2021 An Intriguing Globular Cluster in the Galactic Bulge from the VVV Survey ? D. Minniti1; 2, T. Palma3, D. Camargo4, M. Chijani-Saballa1, J. Alonso-García5; 6, J. J. Clariá3, B. Dias7, M. Gómez1, J. B. Pullen1, and R. K. Saito8 1 Departamento de Ciencias Físicas, Facultad de Ciencias Exactas, Universidad Andres Bello, Fernández Concha 700, Las Condes, Santiago, Chile 2 Vatican Observatory, Vatican City State, V-00120, Italy 3 Observatorio Astronómico, Universidad Nacional de Córdoba, Laprida 854, 5000 Córdoba, Argentina 4 Colégio Militar de Porto Alegre, Ministério da Defesa, Av. José Bonifácio 363, Porto Alegre, 90040-130, RS, Brazil 5 Centro de Astronomía (CITEVA), Universidad de Antofagasta, Av. Angamos 601, Antofagasta, Chile 6 Millennium Institute of Astrophysics, Nuncio Monseñor Sotero Sanz 100, Of. 104, Providencia, Santiago, Chile 7 Instituto de Alta Investigación, Sede Iquique, Universidad de Tarapacá, Av. Luis Emilio Recabarren 2477, Iquique, Chile 8 Departamento de Física, Universidade Federal de Santa Catarina, Trindade 88040-900, Florianópolis, SC, Brazil Received ; Accepted ABSTRACT Context. Globular clusters (GCs) are the oldest objects known in the Milky Way so each discovery of a new GC is astrophysically important. In the inner Galactic bulge regions these objects are difficult to find due to extreme crowding and extinction. However, recent near-IR Surveys have discovered a number of new bulge GC candidates that need to be further investigated. Aims. Our main objective is to use public data from the Gaia Mission, the VISTA Variables in the Via Lactea Survey (VVV), the Two Micron All Sky Survey (2MASS), and the Wide-field Infrared Survey Explorer (WISE) in order to measure the physical parameters of Minni 48, a new candidate globular star cluster located in the inner bulge of the Milky Way at l = 359:35 deg, b = 2:79 deg.
    [Show full text]
  • Hypervelocity Stars Ejected from the Galactic Center
    Hypervelocity Stars Ejected from the Galactic Center The Milky Way Halo Conference May 31, 2007 Warren R. Brown Smithsonian Astrophysical Observatory Collaborators: Margaret Geller, Scott Kenyon, Michael Kurtz Hypervelocity stars (HVSs) are stars traveling with such extreme speeds that they are no longer bound to the Galaxy. Hypervelocity stars are interesting because they must be ejected by a massive black hole. As a result, hypervelocity stars give us tools to understand the history stellar interactions with the massive black hole and environment of stars around it. 1 The Milky Way Kaufmann If this is a picture of the Milky Way, the hypervelocity stars we are finding are deep in the halo, at distances of 50 – 100 kpc. The hypervelocity stars we are finding are also B-type stars. B-type stars are stars that are more massive and much more luminous than the Sun. Because B stars burn their fuel very rapidly, they have relatively short lifetimes of order 100 million years. In 1947, Humanson and Zwicky first reported B-type stars at high Galactic latitudes. Because B stars are born in the disk and live only a short time, you wouldn’t expect to find B stars very deep in the halo. Spectroscopic surveys show that the high- latitude B stars are a mix of evolved (horizontal branch) stars that belong to the halo and some main sequence, so-called “run-away B stars.” These run-away B stars all have travel times constant with a disk origin. Run-away stars are explained by two mechanisms: ejections from stellar binary encounters in young star clusters, or when a former binary companion goes supernova.
    [Show full text]
  • Plotting Variable Stars on the H-R Diagram Activity
    Pulsating Variable Stars and the Hertzsprung-Russell Diagram The Hertzsprung-Russell (H-R) Diagram: The H-R diagram is an important astronomical tool for understanding how stars evolve over time. Stellar evolution can not be studied by observing individual stars as most changes occur over millions and billions of years. Astrophysicists observe numerous stars at various stages in their evolutionary history to determine their changing properties and probable evolutionary tracks across the H-R diagram. The H-R diagram is a scatter graph of stars. When the absolute magnitude (MV) – intrinsic brightness – of stars is plotted against their surface temperature (stellar classification) the stars are not randomly distributed on the graph but are mostly restricted to a few well-defined regions. The stars within the same regions share a common set of characteristics. As the physical characteristics of a star change over its evolutionary history, its position on the H-R diagram The H-R Diagram changes also – so the H-R diagram can also be thought of as a graphical plot of stellar evolution. From the location of a star on the diagram, its luminosity, spectral type, color, temperature, mass, age, chemical composition and evolutionary history are known. Most stars are classified by surface temperature (spectral type) from hottest to coolest as follows: O B A F G K M. These categories are further subdivided into subclasses from hottest (0) to coolest (9). The hottest B stars are B0 and the coolest are B9, followed by spectral type A0. Each major spectral classification is characterized by its own unique spectra.
    [Show full text]
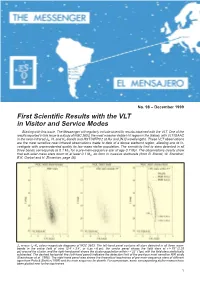
  • First Scientific Results with the VLT in Visitor and Service Modes
    No. 98 – December 1999 First Scientific Results with the VLT in Visitor and Service Modes Starting with this issue, The Messenger will regularly include scientific results obtained with the VLT. One of the results reported in this issue is a study of NGC 3603, the most massive visible H II region in the Galaxy, with VLT/ISAAC in the near-infrared Js, H, and Ks-bands and HST/WFPC2 at Hα and [N II] wavelengths. These VLT observations are the most sensitive near-infrared observations made to date of a dense starburst region, allowing one to in- vestigate with unprecedented quality its low-mass stellar population. The sensitivity limit to stars detected in all three bands corresponds to 0.1 M0 for a pre-main-sequence star of age 0.7 Myr. The observations clearly show that sub-solar-mass stars down to at least 0.1 M0 do form in massive starbursts (from B. Brandl, W. Brandner, E.K. Grebel and H. Zinnecker, page 46). Js versus Js–Ks colour-magnitude diagrams of NGC 3603. The left-hand panel contains all stars detected in all three wave- bands in the entire field of view (3.4′×3.4′, or 6 pc × 6 pc); the centre panel shows the field stars at r > 75″ (2.25 pc) around the cluster, and the right-hand panel shows the cluster population within r < 33″ (1pc) with the field stars statistically subtracted. The dashed horizontal line (left-hand panel) indicates the detection limit of the previous most sensitive NIR study (Eisenhauer et al.
    [Show full text]
  • A Near-Infrared Photometric Survey of Metal-Poor Inner Spheroid Globular Clusters and Nearby Bulge Fields
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server A Near-Infrared Photometric Survey of Metal-Poor Inner Spheroid Globular Clusters and Nearby Bulge Fields T. J. Davidge 1 Canadian Gemini Office, Herzberg Institute of Astrophysics, National Research Council of Canada, 5071 W. Saanich Road, Victoria, B. C. Canada V8X 4M6 email:[email protected] ABSTRACT Images recorded through J; H; K; 2:2µm continuum, and CO filters have been obtained of a sample of metal-poor ([Fe/H] 1:3) globular clusters ≤− in the inner spheroid of the Galaxy. The shape and color of the upper giant branch on the (K; J K) color-magnitude diagram (CMD), combined with − the K brightness of the giant branch tip, are used to estimate the metallicity, reddening, and distance of each cluster. CO indices are used to identify bulge stars, which will bias metallicity and distance estimates if not culled from the data. The distances and reddenings derived from these data are consistent with published values, although there are exceptions. The reddening-corrected distance modulus of the Galactic Center, based on the Carney et al. (1992, ApJ, 386, 663) HB brightness calibration, is estimated to be 14:9 0:1. The mean ± upper giant branch CO index shows cluster-to-cluster scatter that (1) is larger than expected from the uncertainties in the photometric calibration, and (2) is consistent with a dispersion in CNO abundances comparable to that measured among halo stars. The luminosity functions (LFs) of upper giant branch stars in the program clusters tend to be steeper than those in the halo clusters NGC 288, NGC 362, and NGC 7089.
    [Show full text]
  • Download This Article in PDF Format
    A&A 601, A29 (2017) Astronomy DOI: 10.1051/0004-6361/201629685 & c ESO 2017 Astrophysics Delay-time distribution of core-collapse supernovae with late events resulting from binary interaction E. Zapartas1, S. E. de Mink1, R. G. Izzard2, S.-C. Yoon3, C. Badenes4, Y. Götberg1, A. de Koter1; 5, C. J. Neijssel1, M. Renzo1, A. Schootemeijer6, and T. S. Shrotriya6 1 Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands e-mail: [E.Zapartas;S.E.deMink]@uva.nl 2 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 3 Astronomy Program, Department of Physics and Astronomy, Seoul National University, 151–747 Seoul, Korea 4 Department of Physics and Astronomy & Pittsburgh Particle Physics, Astrophysics, and Cosmology Center (PITT-PACC), University of Pittsburgh, Pittsburgh, PA 15260, USA 5 Institute of Astronomy, KU Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium 6 Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany Received 11 September 2016 / Accepted 1 January 2017 ABSTRACT Most massive stars, the progenitors of core-collapse supernovae, are in close binary systems and may interact with their companion through mass transfer or merging. We undertake a population synthesis study to compute the delay-time distribution of core-collapse supernovae, that is, the supernova rate versus time following a starburst, taking into account binary interactions. We test the systematic robustness of our results by running various simulations to account for the uncertainties in our standard assumptions. We find that +9 a significant fraction, 15−8%, of core-collapse supernovae are “late”, that is, they occur 50–200 Myr after birth, when all massive single stars have already exploded.
    [Show full text]
  • Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects
    Juliana Crestani Ribeiro de Souza Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects Porto Alegre 2017 Juliana Crestani Ribeiro de Souza Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects Dissertação elaborada sob orientação do Prof. Dr. Eduardo Luis Damiani Bica, co- orientação do Prof. Dr. Charles José Bon- ato e apresentada ao Instituto de Física da Universidade Federal do Rio Grande do Sul em preenchimento do requisito par- cial para obtenção do título de Mestre em Física. Porto Alegre 2017 Acknowledgements To my parents, who supported me and made this possible, in a time and place where being in a university was just a distant dream. To my dearest friends Elisabeth, Robert, Augusto, and Natália - who so many times helped me go from "I give up" to "I’ll try once more". To my cats Kira, Fen, and Demi - who lazily join me in bed at the end of the day, and make everything worthwhile. "But, first of all, it will be necessary to explain what is our idea of a cluster of stars, and by what means we have obtained it. For an instance, I shall take the phenomenon which presents itself in many clusters: It is that of a number of lucid spots, of equal lustre, scattered over a circular space, in such a manner as to appear gradually more compressed towards the middle; and which compression, in the clusters to which I allude, is generally carried so far, as, by imperceptible degrees, to end in a luminous center, of a resolvable blaze of light." William Herschel, 1789 Abstract We provide a sample of 170 Galactic Globular Clusters (GCs) and analyse its spatial distribution properties.
    [Show full text]
  • Exep Science Plan Appendix (SPA) (This Document)
    ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 1 of 61 Created By: David A. Breda Date Program TDEM System Engineer Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology Dr. Nick Siegler Date Program Chief Technologist Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology Concurred By: Dr. Gary Blackwood Date Program Manager Exoplanet Exploration Program NASA/Jet Propulsion Laboratory California Institute of Technology EXOPDr.LANET Douglas Hudgins E XPLORATION PROGRAMDate Program Scientist Exoplanet Exploration Program ScienceScience Plan Mission DirectorateAppendix NASA Headquarters Karl Stapelfeldt, Program Chief Scientist Eric Mamajek, Deputy Program Chief Scientist Exoplanet Exploration Program JPL CL#19-0790 JPL Document No: 1735632 ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 2 of 61 Approved by: Dr. Gary Blackwood Date Program Manager, Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory Dr. Douglas Hudgins Date Program Scientist Exoplanet Exploration Program Science Mission Directorate NASA Headquarters Created by: Dr. Karl Stapelfeldt Chief Program Scientist Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory California Institute of Technology Dr. Eric Mamajek Deputy Program Chief Scientist Exoplanet Exploration Program Office NASA/Jet Propulsion Laboratory California Institute of Technology This research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. © 2018 California Institute of Technology. Government sponsorship acknowledged. Exoplanet Exploration Program JPL CL#19-0790 ExEP Science Plan, Rev A JPL D: 1735632 Release Date: February 15, 2019 Page 3 of 61 Table of Contents 1.
    [Show full text]
  • Exoplanetary Atmospheres: Key Insights, Challenges, and Prospects
    AA57CH15_Madhusudhan ARjats.cls August 7, 2019 14:11 Annual Review of Astronomy and Astrophysics Exoplanetary Atmospheres: Key Insights, Challenges, and Prospects Nikku Madhusudhan Institute of Astronomy, University of Cambridge, Cambridge CB3 0HA, United Kingdom; email: [email protected] Annu. Rev. Astron. Astrophys. 2019. 57:617–63 Keywords The Annual Review of Astronomy and Astrophysics is extrasolar planets, spectroscopy, planet formation, habitability, atmospheric online at astro.annualreviews.org composition https://doi.org/10.1146/annurev-astro-081817- 051846 Abstract Copyright © 2019 by Annual Reviews. Exoplanetary science is on the verge of an unprecedented revolution. The All rights reserved thousands of exoplanets discovered over the past decade have most recently been supplemented by discoveries of potentially habitable planets around nearby low-mass stars. Currently, the field is rapidly progressing toward de- tailed spectroscopic observations to characterize the atmospheres of these planets. Various surveys from space and the ground are expected to detect numerous more exoplanets orbiting nearby stars that make the planets con- ducive for atmospheric characterization. The current state of this frontier of exoplanetary atmospheres may be summarized as follows. We have entered the era of comparative exoplanetology thanks to high-fidelity atmospheric observations now available for tens of exoplanets. Access provided by Florida International University on 01/17/21. For personal use only. Annu. Rev. Astron. Astrophys. 2019.57:617-663. Downloaded from www.annualreviews.org Recent studies reveal a rich diversity of chemical compositions and atmospheric processes hitherto unseen in the Solar System. Elemental abundances of exoplanetary atmospheres place impor- tant constraints on exoplanetary formation and migration histories.
    [Show full text]
  • Globular Clusters in the Inner Galaxy Classified from Dynamical Orbital
    MNRAS 000,1{17 (2019) Preprint 14 November 2019 Compiled using MNRAS LATEX style file v3.0 Globular clusters in the inner Galaxy classified from dynamical orbital criteria Angeles P´erez-Villegas,1? Beatriz Barbuy,1 Leandro Kerber,2 Sergio Ortolani3 Stefano O. Souza 1 and Eduardo Bica,4 1Universidade de S~aoPaulo, IAG, Rua do Mat~ao 1226, Cidade Universit´aria, S~ao Paulo 05508-900, Brazil 2Universidade Estadual de Santa Cruz, Rodovia Jorge Amado km 16, Ilh´eus 45662-000, Brazil 3Dipartimento di Fisica e Astronomia `Galileo Galilei', Universit`adi Padova, Vicolo dell'Osservatorio 3, Padova, I-35122, Italy 4Universidade Federal do Rio Grande do Sul, Departamento de Astronomia, CP 15051, Porto Alegre 91501-970, Brazil Accepted XXX. Received YYY; in original form ZZZ ABSTRACT Globular clusters (GCs) are the most ancient stellar systems in the Milky Way. There- fore, they play a key role in the understanding of the early chemical and dynamical evolution of our Galaxy. Around 40% of them are placed within ∼ 4 kpc from the Galactic center. In that region, all Galactic components overlap, making their disen- tanglement a challenging task. With Gaia DR2, we have accurate absolute proper mo- tions for the entire sample of known GCs that have been associated with the bulge/bar region. Combining them with distances, from RR Lyrae when available, as well as ra- dial velocities from spectroscopy, we can perform an orbital analysis of the sample, employing a steady Galactic potential with a bar. We applied a clustering algorithm to the orbital parameters apogalactic distance and the maximum vertical excursion from the plane, in order to identify the clusters that have high probability to belong to the bulge/bar, thick disk, inner halo, or outer halo component.
    [Show full text]