Uva-DARE (Digital Academic Repository)
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
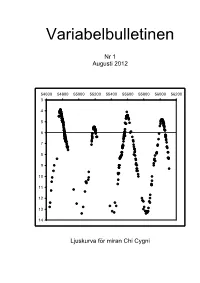
Variabelbulletinen Nr. 1
Variabelbulletinen Nr 1 Augusti 2012 54600 54800 55000 55200 55400 55600 55800 56000 56200 3 4 5 6 7 8 9 10 11 12 13 14 Ljuskurva för miran Chi Cygni 2 Variabelbulletinen Nr 1. Augusti 2012. ISSN 2001-3930 En publikation från Svensk AmatörAstronomisk Förening Variabelsektionen (SAAF/V) Sektionsledare Chris Allen Ansvariga för databasen SVO Thomas Karlsson och Robert Wahlström Redaktör Hans Bengtsson Icke signerat material har författats av redaktören. Innehållsförteckning Introduktion. …………………...…………………………………………………………………….……………………….…… 4 Hans Bengtsson: Klassiska miror och legendariska variabilister. ………………...…….…..... 4 Thomas Karlsson: Epsilon Aurigae. ….……………………...……………………………...………………..…. 16 Hans Bengtsson: Våra variabler. Första delen. ………………………………………..…….....….……. 16 Thomas Karlsson: Ljusstark supernova i M101. ………………………………………………..…….… 26 Gustav Holmberg: Några RCB-stjärnor säsongen 2011-2012. …....…………...……….……. 28 Thomas Karlsson: Bestämning av period för 58 variabler. …………..……………...……….…... 31 Thomas Karlsson: Maxima för miror. ………………………………………………………………...……….… 33 Thomas Karlsson: Fotometri i Sagitta och Vulpecula. …………………………………………….… 34 Statistisk från SVO. ……………..…………………………………………...………………………………………...…… 38 Hans Bengtsson: Variabelmöten – en ny tradition. …………...……………………………………….. 39 Hans Bengtsson: Flera flugor i samma smäll. …………………………...............................…………... 40 Förstasidan Ljuskurva för miran Chi Cygni. Följande observatörer har bidragit till diagrammet: Chris Allen (45), Hans Bengtsson (102), Göran Fredriksson (9), -

1903Aj 23 . . . 22K 22 the Asteojsomic Al
22 THE ASTEOJSOMIC AL JOUENAL. Nos- 531-532 22K . Taking into account the smallness of the weights in- concerned. Through the use of these tables the positions . volved, the individual differences which make up the and motions of many stars not included in the present 23 groups in the preceding table agree^very well. catalogue can be brought into systematic harmony with it, and apparently without materially less accuracy for the in- dividual stars than could be reached by special compu- Tables of Systematic Correction for N2 and A. tations for these stars in conformity with the system of B. 1903AJ The results of the foregoing comparisons. have been This is especially true of the star-places computed by utilized to form tables of systematic corrections for ISr2, An, Dr. Auwers in the catalogues, Ai and As. As will be seen Ai and As. In right-ascension no distinction is necessary by reference to the catalogue the positions and motions of between the various catalogues published by Dr. Auwers, south polar stars taken from N2 agree better with the beginning with the Fundamental-G at alo g ; but in decli- results of this investigation than do those taken from As, nation the distinction between the northern, intermediate, which, in turn, are quoted from the Cape Catalogue for and southern catalogues must be preserved, so far as is 1890. SYSTEMATIC COBEECTIOEB : CEDEE OF DECLINATIONS. Eight-Ascensions ; Cokrections, ¿las and 100z//xtf. Declinations; Corrections, Æs and IOOzZ/x^. B — ISa B —A B —N2 B —An B —Ai âas 100 â[is âas 100 âgô âSs 100 -

Astrobiology Math
National Aeronautics andSpace Administration Aeronautics National Astrobiology Math This collection of activities is based on a weekly series of space science problems intended for students looking for additional challenges in the math and physical science curriculum in grades 6 through 12. The problems were created to be authentic glimpses of modern science and engineering issues, often involving actual research data. The problems were designed to be one-pagers with a Teacher’s Guide and Answer Key as a second page. This compact form was deemed very popular by participating teachers. Astrobiology Math Mathematical Problems Featuring Astrobiology Applications Dr. Sten Odenwald NASA / ADNET Corp. [email protected] Astrobiology Math i http://spacemath.gsfc.nasa.gov Acknowledgments: We would like to thank Ms. Daniella Scalice for her boundless enthusiasm in the review and editing of this resource. Ms. Scalice is the Education and Public Outreach Coordinator for the NASA Astrobiology Institute (NAI) at the Ames Research Center in Moffett Field, California. We would also like to thank the team of educators and scientists at NAI who graciously read through the first draft of this book and made numerous suggestions for improving it and making it more generally useful to the astrobiology education community: Dr. Harold Geller (George Mason University), Dr. James Kratzer (Georgia Institute of Technology; Doyle Laboratory) and Ms. Suzi Taylor (Montana State University), For more weekly classroom activities about astronomy and space visit the Space Math@ NASA website, http://spacemath.gsfc.nasa.gov Image Credits: Front Cover: Collage created by Julie Fletcher (NAI), molecule image created by Jenny Mottar, NASA HQ. -

1 R PUBLICATIONS of VARIABLE STAR SEQTI ROYAL
C. No. 18 (?992) o Mniim.nmMii: IIIMIlJV : 1—r 1 r FIGURE S PUBLICATIONS of 7 VARIABLE STAR SEQTI f ROYAL ASTRONOMICAL SOCIETY 1 1 OF NEW ZEALAND to to it li a /4 '4 5t#a^B ill- « I to JUSGR Director: Frank M. Bateson it P.O. Box 3093, GREERTON, TAURANGA, NEW ZEALAND. H a i ISSN 0111-736X PUBLICATIONS OF THE VARIABLE STAR SECTION ROYAL ASTRONOMICAL SOCIETY NEW ZEALAND" No. 18 CONTENTS i & ii. INDEX iii. EDITORIAL 1. THE LIGHT CURVE OF RU PEGASI 1980 - 1992 F.M. Bateson, R. Mcintosh & D. Brunt 8. NOVA SCORPII 1992 - PRELIMINARY LIGHT CURVE Ranald Mcintosh 11. VISUAL OBSERVATIONS OF BL TELESCOPII Peter F. Williams 17. A POSSIBLE OUTBURST OF V4-30 CARINAE M. Morel 22. OBSERVATIONS OF THE TRANSIENT X-RAY SOURCE AO538-66 Frank M. Bateson 28. THE DISCOVERY OF NOVA PUPPIS 1991 Paul Camilleri 30. THE LIGHT CURVE OF NOVA PUPPIS 1991 Frank M. Bateson 32. TWO COLOUR SEQUENCE FOR 0525J52 TV COLUMBAE P.M. Kilmartin 33. THE SEMI-REGULAR VARIABLE RX LEPORIS Frank M. Bateson 37. THE FADING OF S DORADUS F.M. Bateson & A.F. Jones 41. OUTBURSTS OF THE DWARF NOVA IP PEGASI Frank M. Bateson ii PUBLICATIONS OF THE VARIABLE STAR SECTION ROYAL ASTRONOMICAL SOCIETY NEW ZEALAND No. 18 CONTENTS (cont.) 45o LIGHT CURVES OF SOME MIRA VARIABLES Ranald Mcintosh & Don Brunt 46. (a) S PICTORIS J.D. 2,426,800 - 2,448,775 Figs. 1 - 8 54. (b) T CENTAURI J.D. 2,425,450 - 2,448,680 Figs. 9 - 16 62. -

Joint Meeting of the American Astronomical Society & The
American Association of Physics Teachers Joint Meeting of the American Astronomical Society & Joint Meeting of the American Astronomical Society & the 5-10 January 2007 / Seattle, Washington Final Program FIRST CLASS US POSTAGE PAID PERMIT NO 1725 WASHINGTON DC 2000 Florida Ave., NW Suite 400 Washington, DC 20009-1231 MEETING PROGRAM 2007 AAS/AAPT Joint Meeting 5-10 January 2007 Washington State Convention and Trade Center Seattle, WA IN GRATITUDE .....2 Th e 209th Meeting of the American Astronomical Society and the 2007 FOR FURTHER Winter Meeting of the American INFORMATION ..... 5 Association of Physics Teachers are being held jointly at Washington State PLEASE NOTE ....... 6 Convention and Trade Center, 5-10 January 2007, Seattle, Washington. EXHIBITS .............. 8 Th e AAS Historical Astronomy Divi- MEETING sion and the AAS High Energy Astro- REGISTRATION .. 11 physics Division are also meeting in LOCATION AND conjuction with the AAS/AAPT. LODGING ............ 12 Washington State Convention and FRIDAY ................ 44 Trade Center 7th and Pike Streets SATURDAY .......... 52 Seattle, WA AV EQUIPMENT . 58 SUNDAY ............... 67 AAS MONDAY ........... 144 2000 Florida Ave., NW, Suite 400, Washington, DC 20009-1231 TUESDAY ........... 241 202-328-2010, fax: 202-234-2560, [email protected], www.aas.org WEDNESDAY..... 321 AAPT AUTHOR One Physics Ellipse INDEX ................ 366 College Park, MD 20740-3845 301-209-3300, fax: 301-209-0845 [email protected], www.aapt.org Acknowledgements Acknowledgements IN GRATITUDE AAS Council Sponsors Craig Wheeler U. Texas President (6/2006-6/2008) Ball Aerospace Bob Kirshner CfA Past-President John Wiley and Sons, Inc. (6/2006-6/2007) Wallace Sargent Caltech Vice-President National Academies (6/2004-6/2007) Northrup Grumman Paul Vanden Bout NRAO Vice-President (6/2005-6/2008) PASCO Robert W. -

On the Physical Environment in Galactic Nuclei
i yy, `!-+^fw-+Ye.-.rte... e., :. .• t ^' f Technical Memorandum 80569 On the Physical Environment In Galactic Nuclei J. H. Beall- (11ASA-TM-80569) ON THE PHYSICAL ENVIRONMENT N80-17939 IN THE GALACTIC NUCLEI Ph.D. Thesis - Maryland Univ. (NASA) 190 p HC A09/MF A01 CSCL 03B Unclas G3/90 12893 SEPTEMBER 1979 National Aeronautics and Space Administration Goddard Space Flight Center l s " GreenWt, Maryland 20771 R^ Lij LM ^^ ca A CnMr. .t47 may` - 4 —jr, l r P= ON ThE PHYSICAL ENVI90NMENT IN GALACTIC NUCLEI* r ^;y James Howard Beall DISSERTATION SUBMITZED TO THE FACULTY OF THE GRADUATE SCHOOL CF 28E UNIVERSITY OF MARYLAND IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY 1979 *Wcrk sue ao rted by NASA Grant NGF 21-002-316 r ABSTRACT On the Fhysical Environment in Galactic Nuclei, James koward Beall, Doctor of Philosophy, 1979 Dissertation directed by N.R. Rose Professor Eepartment of Physics,and Astronomy Galactic nuclei and 9 ,e.-isars exit radiation over the entire electromagnetic spectrum. There is considerable interest in the nature of the emission mechanisms which may be responsible for the observed radiation. The possibility that a single mechanism is responsible for a wide frequency range of the electromagnetic flux suggests that multiple frequency observations of galactic nuclei and l a cars can be used to place constraints on models for the source •vchanisms. involved. f In conjunction with observations by the High Energy 2—ray Spectrometer on OSO-8, four sources have been investigated in this manner: (i) the nucleus of the elliptical galaxy, f Centaurus A (NGC 5128) ; (ii) the quasar, 3C273; 6 (iii) the nucleus of the Seyfert galaxy, NGC 4151; and (iv) the nucleus of the !Milky Way galaxy. -

Fundamental Problems in the Evaluation of Electron Micrographs
RIJKSUNIVERSITEIT TE GRONINGEN FUNDAMENTAL PROBLEMS IN THE EVALUATION OF ELECTRON MICROGRAPHS Proefschrift ter verkrijging van het doctoraat in de Wiskunde en Natuurwetenschappen aan de Rijksuniversiteit te Groningen op gezag van de Rector Magnificus Dr. J. Borgman in het openbaar te verdedigen op vrijdag 23 februari 1979 des namiddags te 2.45 uur precies door ANDRE MARTINUS JAN HUISER geboren te Groningen I Promotor: Dr. H. A. Ferwerda Coreferent: Prof. Dr. Ir. H. J. Frankena I r. tev nagedaehtenis van mijn vader ••./»'• VOORWOORD Graag wil ik diegenen bedanken met wie ik heb samengewerkt tijdens mijn promotie onderzoek. Zonder de ongenoemden te kort te willen doen wil ik enkelen met name noemen. In de eerste plaats mijn promotor, Dr. H.A. Ferwerda. Hem ben ik zeer erkentelijk voor de critische belangstelling waarmee hij mijn werk begeleid heeft en vooral voor zijn sympatieke wijze van samen- werking. Bij het schrijven van dit proefschrift heb ik veel steun ondervon- den van mijn coreferent, Dr. Ir. H.J. Frankena. Van zijn opmerkingen en suggesties heb ik in korte tijd veel geleerd. Hiervoor wil ik hem heel hartelijk danken. Verder ben ik grote dank verschuldigd aan Dr. B. J. Hoenders, Ir. P. van Toorn, en Dr. A.H. Greenaway voor hun tegenspel in de talloze discussies op wetenschappelijk en niet wetenschappelijk terrein, in en buiten het laboratorium. Zonder hun zouden belangrijke onderdelen van dit proefschrift wellicht nooit zijn ontstaan. Niet in het minst ben ik dank verschuldigd aan Sietske Lutter voor de aanstekelijke opgewektheid waarmee zij het leeuwendeel van dit proefschrift getypt heeft; alsmede Elli Boswijk die ook een gedeelte van het typewerk voor haar rekening heeft genomen. -

2010/7-8 • a Nagy Magellán-Felhő
július- 2010/7-8 • augusztus A Nagy Magellán-felhõ TARTALOM Világító lampionok . 3 Kutatások az ELTE-n . 4 Napfizika Debrecenben . 7 Csillagászati hírek . 10 Csiba Márton (1937–2010) . 23 Csillagászattörténet A Magyar Csillagászati Egyesület lapja Üstökös tsillag a templomtornyon . 24 Journal of the Hungarian Astronomical Association A II. Csillagászattörténeti Találkozó . 27 H–1300 Budapest, Pf. 148., Hungary Szakkör a Polarisban . 29 1037 Budapest, Laborc u. 2/C. Galilei 1610–2010 TELEFON/FAX: (1) 240-7708, +36-70-548-9124 Galilei csillagai alatt . 35 (hétköznap 8–20-óráig) Egy Galilei-élmény . 38 E-MAIL: [email protected] Esti csillagnézõ túrák . 39 meteor.mcse.hu, www.mcse.hu A távcsövek világa hirek.csillagaszat.hu, www.csillagvaros.hu NEAF – NÉzz Az ég Felé! . 43 HU ISSN 0133-249X Új csillagvizsgáló Hajdúhadházon . 51 Egy 304/1525 mm-es Newton-reflektor . 54 FÔSZERKESZTÔ: Mizser Attila Egy év – egy kép . 107 SZERKESZTÔBIZOTTSÁG: A Gyöngyös-patak mentén . 108 Dr. Fûrész Gábor, Dr. Kiss László, Tíz éves a Stella Sopron . 112 Dr. Kereszturi Ákos, Dr. Kolláth Zoltán, Mizser Attila, Jelenségnaptár . 115 Sánta Gábor, Sárneczky Krisztián, Dr. Szabados Programajánló . 119 László és Szalai Tamás Asztrofotósként Namíbiában . 120 SZÍNES ELÕKÉSZÍTÉS: VIZI PÉTER Képmelléklet . 132 A Meteor elôfizetési díja 2010-re: (nem tagok számára) 6400 Ft meGFIGYELÉsek Egy szám ára: 550 Ft Meteorok Kiadványunkat az MCSE tagjai Videometeoros észlelések 2009-ben . 57 illetményként kapják! Hold FELELÔS KIADÓ: az MCSE elnöke A Fra Mauro-kráter . 60 Üstökösök Az egyesületi tagság formái (2010) Tavaszi zsongás . 66 • rendes tagsági díj (jogi személyek számára is) Változócsillagok (illetmény: Meteor+ Visszatérõ nóvák másodlagos változásai . 72 Meteor csill. -

A New Binary Be Star Detected by VLTI/AMBER Spectro-Interferometry
A&A 488, L67–L70 (2008) Astronomy DOI: 10.1051/0004-6361:200810624 & c ESO 2008 Astrophysics Letter to the Editor δ Centauri: a new binary Be star detected by VLTI/AMBER spectro-interferometry A. Meilland1,F.Millour1,Ph.Stee2,A.Spang2, R. Petrov2, D. Bonneau2, K. Perraut3, and F. Massi4 1 Max Planck Intitut fur Radioastronomie, Auf dem Hugel 69, 53121 Bonn, Germany e-mail: [email protected] 2 Laboratoire A.H. FIZEAU, UMR 6525, UNS/OCA/CNRS, Campus Valrose, 06108 Nice Cedex 2, France 3 Laboratoire d’Astrophysique de Grenoble, UMR 5571 Université Joseph Fourier/CNRS, BP 53, 38041 Grenoble Cedex 9, France 4 INAF – Osservatorio Astrofisico di Arcetri, Istituto Nazionale di Astrofisica, Largo E. Fermi 5, 50125 Firenze, Italy Received 16 July 2008 / Accepted 29 July 2008 ABSTRACT Aims. We study the Be star δ Cen circumstellar disk using long-baseline interferometry which is the only observing technique capable of resolving spatially and spectroscopically objects smaller than 5 mas in the H and K band. Methods. We used the VLTI/AMBER instrument on January 6, 8, and 9, 2008, in the H and K bands to complete low (35) and medium (1500) spectral resolution observations. Results. We detected an oscillation in the visibility curve plotted as a function of the spatial frequency which is a clear signature of a companion around δ Cen. Our best-fit soltution infers a binary separation of 68.7 mas, a companion flux contribution in the K band of about 7% of the total flux, a PA of 117.5◦, and an envelope flux around the Be primary that contributes up to about 50% of the total flux, in agreement with our Spectral Energy Distribution (SED) fit. -

VSS Newsletter – May 2009
Newsletter 2009/2 2009 May From the Director The opening bars of the first movement Sometimes I feel like the conductor of an orchestra – I wave a wand but everyone else produces the real music. And that’s the way it is in these early days of VSS. A priority for me has been to recruit people far better qualified than I to develop the various spe- cialist areas of VSS. In addition to Stan Walker in LPVs and Alan Plummer in Visual, we now have Dr Paddy McGee of Adelaide to handle CVs. With a PhD in CVs and a range of valuable collabora- tions, it would be hard to find better. I’m really looking forward to see what Paddy comes up with for us. Bob Evans of Invercargill has kindly agreed to handle membership and finance for VSS. Thank God you’re here, Bob! Membership already stands at 20, and I’d expect more to sign up at the RASNZ Conference. A membership form is in the back of this Newsletter. Remember, only VSS members can partake in VSS Projects. After much arm-twisting, I’ve finally persuaded me to take on the role of Coordinator of the Eclips- ing Binaries Programme. I’ve got a couple of projects in mind that I’ll discuss later in this Newsletter, but I confess I’ve been too busy running this show to have anything concrete yet. Which is why a Director shouldn’t be a Coordinator. Anyone want to take Eclipsers away from me, please? Pleeeease? Everyone is waiting on what Michael Chapman will produce for our website, www.varstars.org. -

Download VSS Annual Report 2015
VARIABLE STARS SOUTH An interesting innovation was set up by Carl Royal Astronomical Society of New Zealand, Knight of Manawatu who helped a local year Variable Star Section 11student, Tessa Hiscox of Freyberg High School, in a practical project involving CCD measures of Active membership continued to increase in 2015 the Cepheid, UU Muscae, for her participation in with more than a dozen additions, some of whom the August 2015 science fair in Palmerston North. This made presentations at conferences or published resulted in a Distinction Prize for Tessa but the refereed papers. more lasting and practical result has been a series of meetings with school science teachers in the Members also attended conferences; eight were at area and a general discussion about what the Mt John Anniversary Symposium with fifteen cooperation is practical and realistic. or more at the associated RASNZ Annual Conference. A poster paper was presented at the Also in the outreach area Alan Plummer continues former, two spoken papers and three posters were to write a monthly article for Sky & Telescope, presented at the latter. As well, our editor, Phil Australia, Alan Baldwin contributes items for the Evans, attended a meeting in Hawaii of current and RASNZ newsletter, Stan Walker has written past Swinburne University master’s students where he articles for Southern Stars and the Auckland introduced VSS to a number of attendees. Andrew Society's Journal and our website, maintained by Pearce, an enthusiastic visual observer, presented David O'Driscoll, is very popular with many a poster paper at the Spring Meeting of the visitors. -

High S/N Echelle Spectroscopy in Young Stellar Groups II. Rotational
A&A manuscript no. (will be inserted by hand later) ASTRONOMY AND Your thesaurus codes are: ASTROPHYSICS 08.05.1; 08.06.2; 08.18.1; 10.15.2 Sco OB2 20.3.2018 High S/N Echelle Spectroscopy in Young Stellar Groups ⋆ II. Rotational Velocities of Early-Type Stars in Sco OB2 A.G.A. Brown@1, W. Verschueren@2,1 @1 Sterrewacht Leiden, P.O. Box 9513, 2300 RA, Leiden, The Netherlands @2 University of Antwerp (RUCA), Astrophysics Research Group, Groenenborgerlaan 171, 2020 Antwerpen, Belgium Received... , accepted... Abstract. We investigate the rotational velocities of 1. Introduction early-type stars in the Sco OB2 association. We measure vsini for 156 established and probable members of the An outstanding problem in theories of star formation association. The measurements are performed with three is the so-called angular momentum problem. Molecular different techniques, which are in increasing order of ex- clouds and cloud cores, even if they spin about their axis pected vsini: 1) converting the widths of spectral lines di- only once per Galactic rotation, contain much more an- rectly to vsini, 2) comparing artificially broadened spectra gular momentum than the stars that form from them (see of low vsini stars to the target spectrum, 3) comparing the e.g., Spitzer 1968). Observations suggest that an inter- i He λ4026 line profile to theoretical models. The sample is stellar parent cloud must lose at least two to four or- extended with literature data for 47 established members ders of magnitude of angular momentum for a relatively of Sco OB2. Analysis of the vsini distributions shows that wide binary system and a single star, respectively, to be- there are no significant differences between the subgroups come dynamically possible (see Mouschovias 1991).