Probability: More Examples & Concepts
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

CREATIVE QUARTER CREATIVE QUARTER November 2016
Programme CREATIVE QUARTER CREATIVE QUARTER November 2016 Creative Quarter is a day of free events in South Kensington offering young people the chance to explore work in the creative industries and creative careers. Leading science and art institutions are inviting school groups to participate in a programme of talks, workshops and behind the scenes tours with some of the UK’s leading creative and scientific professionals. Places are free but advance booking for talks and workshops is essential. We will also have a great programme of drop-in events to complement the booked events as well as lots of fascinating exhibitions and displays. Creative Quarter is a joint event organised by the cultural and educational organisations in Discover South Kensington – home of science, arts and inspiration. www.discoversouthken.com Royal College of Music MUSIC Exploring Careers in Music 10:00 What does a creative career in music look like? From performing to teaching, composing and more, this Royal College of Music session will explore potential musical pathways and feature guest speakers, live music and interactive Amaryllis Fleming Concert Hall, workshop elements. Prince Consort Road, London SW7 2BS BOOKING DETAILS RCM Box Office 020 7591 4314 (Mon-Fri 10am-4pm) MUSIC Beyond the Notes – Performance Masterclass 11:30 – 13:00 This practical masterclass will develop musical creativity, performance and ensemble skills and provide engaging and Royal College of Music useful feedback for AS and A level music students. Amaryllis Fleming Concert Hall, Prince Consort Road, There will be an exciting opportunity for a limited number of participants to share a solo piece or small ensemble, with London SW7 2BS friendly team of experts and small audience. -

Deliveries Map South Kensington Campus
South Kensington Campus Deliveries Map September 2016 Hyde Park Kensington Gore Royal Albert Hall Prince’s Gate Gardens Prince’s Gate Queen’s Gate Queen’s Beit Quad Ethos Prince Consort Road Sports Centre Blackett Royal School of Mines Royal Prince’s Gardens (North Side) College of Music Bone Roderic Hill Roderic Bessemer Business School ACEX Huxley Prince’s Dalby Court Gardens Electrical Electrical Engineering PR Shereld Faculty Prince’s Gardens (Watts Way) Queen’s City and Lawn Guilds Southside Library Skempton Building Road Exhibition Imperial College Road College Gate Gate NO CARS Chemistry House Chemistry metres Sir RCS1 Alexander Fleming South Frankland Road Kensington No access beyond this point for deliveries Main walkway Catering, Shereld Stores for deliveries (Level 2) Building x Mechanical Engineering/ Chemical Engineering Main entrance Business School x x Electrical and Electronic Physics, Blackett Delivery route Engineering x Laboratory x Post room x Service Point, Shereld PR VWR stores for: SAF, Aeronautics, Huxley, Building x Chemistry, RCS, Flowers Shereld (except ICT, and Sir Ernst Chain Careers, Catering) deliveries x Beit Quadrangle Goldsmiths Building Grantham Institute – Sir Ernst Chain Building – Imperial College Union Huxley Building Climate Change and Wolfson Laboratories Ethos Sports Centre ACE Extension the Environment Flowers Building Prince’s Gdns, North Side William Penney Faculty Building Chemistry Building Weeks Hall Laboratory Prince’s Gate Sir Alexander Fleming Blackett Laboratory 16 Electrical Engineering Queen’s Gate Building Roderic Hill Building Business School Central Library Chemistry RCS Bone Building Prince’s Gate Queen’s Tower Prince’s Gate Royal School of Mines Eastside Skempton Building Alumni Visitor Centre Aston Webb Shereld Building City and Guilds Buildings where Building Bessemer Building Student Hub wheelchair access is Conference Oce Southside not possible at this time. -

ICIC Data Analysis Lecture 1 2014
Course'Team Alan%Heavens% ICIC Data Analysis Workshop Andrew%Jaffe% Principled statistical methods for researchers Jonathan%Pritchard% ! 8-11 September 2014 Daniel%Mortlock% Roberto%Tro;a%% Justin Alsing Hik Shariff Sponsored by STFC ! Rachel Groom and Winton Capital Sandie Bernor South Kensington Campus South Kensington Campus Hyde Park Logis>cs%and%events Kensington Gore Royal Albert • Fire%exits% Hall We • Prince’s Gate I/O:%Tea/coffee/lunch%(Blacke;%311),%toilets% 2 Gardens are e’s Gate Princ here Queen’s Gate • Breakfast%8.15P8.45%a.m.% 1 Beit Quad Prince Consort Road Ethos 3 Sports 45 8 Centre Blackett 7 Royal School 12 • 9 10 of Mines Events:% Prince’s Gardens (North Side) 6 e Bon 11 oderic Hill R Bessemer Business School 17 35 13 14 ACEX • Talk%by%Tom%Babbedge%(Winton)%today%~5%p.m.% al 36 Huxley 16 18 Prince’s 19 15 Gardens Electric Eastside Engineering 22 • Barbecue%tonight%6%p.m.%58%Princes%Gate% 20 Sherfeld 21 Faculty 23 28 25 Prince’s Gardens (Watts Way) Queen’s 26 27 City and Lawn Guilds • Southside Drinks%recep>on%5:30%p.m.%tomorrow% Library Skempton Building 29 24 Exhibition Road 58 Princes Gate Imperial College Road • Public%engagement%lunch,%Wednesday% 30 32 Chemistry 33 Chemistry 50 metres RCS1 31 Sir Alexander 34 Fleming South 4 Frankland Road Kensington Cromwell Road e Thurloe Plac Buildings where wheelchair access is not possible at this time Thurloe Street 1 Beit Quadrangle 12 Goldsmiths Building 21 Grantham Institute 30 Sir Ernst Chain Building – 2 Imperial College Union 13 Huxley Building for Climate Change Wolfson -

Architectural Tour of Exhibition Road and 'Albertopolis'
ARCHITECTURAL TOUR OF EXHIBITION ROAD AND ‘ALBERTOPOLIS’ The area around Exhibition Road and the Albert Hall in Kensington is dominated by some of London’s most striking 19th- and 20th-century public buildings. This short walking tour is intended as an introduction to them. Originally this was an area of fields and market gardens flanking Hyde Park. In 1851, however, the Great Exhibition took place in the Crystal Palace on the edge of the park. It was a phenomenal success and in the late 1850s Exhibition Road was created in commemoration of the event. Other international exhibitions took place in 1862 and 1886 and although almost all the exhibition buildings have now vanished, the institutions that replaced them remain. Queen Victoria’s husband, Prince Albert, had a vision of an area devoted to the arts and sciences. ‘Albertopolis’, as it was dubbed, is evident today in the unique collection of colleges and museums in South Kensington. Begin at Exhibition Road entrance of the V&A: Spiral Building, V&A, Daniel Libeskind, 1996- The tour begins at the Exhibition Road entrance to the V&A, dominated now by a screen erected by Aston Webb in 1909 to mask the original boiler house yard beyond. Note the damage to the stonework, caused by a bomb during the Second World War and left as a memorial. Turn right to walk north up Exhibition Road, 50 yards on your right is the: Henry Cole Wing, V&A, Henry Scott with Henry Cole and Richard Redgrave, 1868-73 Henry Cole was the first director of the South Kensington Museum (now the V&A). -
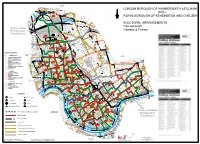
London Borough of Hammersmith & Fulham With
London Borough of Brent BUCKINGHAM BUCKINGHAMHIGH WENDOVER HOLLAND RD AVENUE SPEZIA RD STREET RUCKLIDGE MWS LEGHORN STATION ROAD ROAD RD MONSON BUCHANAN RD WROTTE GDNS ROAD HARLESDEN CAPLE AVENUE RD ROAD LUSHING- RD SLEYTON RD RD RANELAGH RD RD ODESSA HARLEY RD ALL SOULS' GDNS RD AVE BATHURST LONDON BOROUGH OF HAMMERSMITH & FULHAM INGALE R O A D ROAD FURNESS P A L E R M O LANGLER ROAD HONEYWOOD NIGHT ROAD LINDEN AVE TUBBS ROAD CLIFTON ROAD RD PURVES VICTOR COLLEGE FELIXTOWE ROAD HAR ROAD NAPIER RD ROAD ASHBURNHAM RAVENSWORTH STATION Willesden ROW MS GREYHOUND ROAD GDNS PONSARD RD ROAD CHAMBERLANE RD APP LETCHFORD ROAD Junction LETCHFORD BURROWS ROAD VALLIERE GDNS RD S WITH RD BAN. RD ST RIGELEY HARROW MORTIMER CREWE RD RIGELEY MS GDNS ROAD ST Kensal Green ROAD PL RD LANE HOLBERTON MARNE ST WALDO KENMONT GDNS HAZEL ROAD TRENMAR PLOUGH CLOSE WAKEMAN LOTHROP ROAD AVENUE RD CPA HALSTOW STEPHENSON ALMA ROAD STREET BAYF. RD RAINHAM RD OLIPHANT AVE KILRAVOCK LANCEFIELD LANE CPA COMPTON RD PLACE PEMBER RD PEACH GOODHALL Old Oak RD ILBERT STREET PARRY ATLAS CUMBERLAND PK QUEENS ROYAL BOROUGH OF KENSINGTON AND CHELSEA SCRUBS STREET PARK AVENUE Sidings BERENS OAK ENTER COURT STREET FORTUNEWAY BRUCKNER WARF. RD PRISE Hythe Road AVE KILBURN Gateway Kensal Green ST OLD H Y T H E WAY Industrial Trading Estate SIXTH FIFTH HARROW CAIRD ST ROAD Estate ROAD SALTER ROAD STREET St. Mary's HUXLEY ST RIVER ST Cemetery ENBROOK ST ROAD GALTONS ST R D DROOP CL GRAND FOURTH Cemetery STREET ST THIRD LAPF. SALTER BARFETT CL ROAD BASHLEY WARLOCK GDNS ROAD ALPER. -

RBKC 2012/32 Page 1 of 58 the ROYAL BOROUGH OF
THE ROYAL BOROUGH OF KENSINGTON AND CHELSEA TRAFFIC MANAGEMENT ORDER 2012 No. 32 The Kensington and Chelsea (Charged-For Parking Places) Consolidation Order 2012 Made 9th August 2012 Coming into operation: 13th August 2012 ARRANGEMENT OF ARTICLES PART I - PRELIMINARY Article Citation and commencement 1 Revocation of Orders 2 Interpretation 3 PART II - DESIGNATION OF PARKING PLACES Designation of parking places 4 Vehicles for which parking places are designated 5 PART III - SUPPLEMENTARY PROVISIONS Section 1 - General Alteration of position of a vehicle in a parking place 6 Removal of a vehicle from a parking place 7 Movement of a vehicle in a parking place in an emergency 8 Manner of standing in a parking place 9 Manner of waiting in a parking place 10 Restriction on the use of a parking place 11 Restriction on waiting by a vehicle in a parking place 12 Power to suspend the use of a parking place 13 Installation of pay and display machines, placing of traffic signs, etc. 14 Section 2 – The parking charge, maximum parking periods and indications relating to pay and display machines and tickets, etc. Amount of the parking charge at pay and display parking places 15 Payment of the parking charge 16 Indications by ticket and pay and display machine 17 Ticket, pay and display machine and certain permit indications as evidence 18 RBKC 2012/32 Page 1 of 58 No additional payment of a parking charge to be made and no further tickets to be displayed 19 on a vehicle Interval before a vehicle may again be left in a pay and display parking place 20 -

Directions to Imperial College Archives Rcn
DIRECTIONS TO IMPERIAL COLLEGE ARCHIVES RCN Meeting, September 18, 2018 College Archives & Corporate Records Unit Imperial College of Science, Technology and Medicine Anne Barrett College Archivist & Corporate Records Manager Room 455 Sherfield Building London SW7 2AZ Tel: 0207 594 8850 ext: 48850 / 48818 e-mail: [email protected]; [email protected] Directions to Imperial College Archives from South Kensington Station If you take the pedestrian tunnel route, then follow instructions from the red highlighted text after on emerging and turning left (north facing). If you prefer to walk above ground then follow the directions below from the station. Turn right out of the arcade and walk along to the bookshop With your back to the book shop, cross the pedestrian area, pass the café on the corner at your left and continue walking northwards Cross at the lights at the corner with the Thai restaurant opposite you Continue up to the major road, which is Cromwell Road, and cross at the pedestrian crossing Continue up Exhibition Road, past the Natural History and Science Museums on your left Turn second left (first left if using the tunnel) into a private road (Imperial College Road), pass the traffic barrier Walk on to the second right turning by the Queen’s Tower and lawn. Keeping these on your left walk on a short way and at the stone lions turn left. The Sherfield Building will be on your right. Continue walking to the entrance under a covered area straight ahead, and turn right through the automatic doors of the Sherfield Building (building 23 R on the map) Take the lift to level 4 Cross the lift lobby diagonally to your right, following signs to College Archives Go through 1 set of double doors bear left, up a ramp, then through a further 2 sets of double doors; turn left through the last set Room 455 is at the far end of the corridor If you become lost find a telephone and ring extension 48850 (or mobile ring 07714244168) . -

Chapter 3: Delivery Plan
Chapter Three Delivery Plan 3. Delivery Plan 3.1 Introduction This chapter sets out our delivery plan to achieve our LIP objectives, as identified in Chapter 2. It is structured as follows: • Section 3.2 identifies potential funding sources for 2011/12 to 2013/14. • Section 3.3 summarises our delivery actions for this time period and beyond, and describes how the proposed interventions will deliver our LIP objectives. • Section 3.4 sets out our high level programme of investment for this time period (extending to 2015/16 with respect to our proposed major schemes), based on the delivery actions. This section also describes how our more detailed annual programme will be drawn up in the form of an Annual Spending Submission to Transport for London. • Finally, Section 3.5 outlines our approach to programme risk management. 3.2 Potential funding sources Table 3.1 identifies potential funding sources for implementation of our LIP, including our three-year LIP funding allocation from TfL, contributions from the council’s revenue support grant and funding from other sources including developers, local businesses, and specific grants from government (e.g. the Community Infrastructure Fund). These funding levels may vary in total and between individual years of the programme. Our key source of funding is our LIP allocation from TfL, which amounts to £8 million across three years for LIP-funded schemes. We have supplemented this with £15 million of the council’s own funding. This represents a significant investment in our transport networks given the current economic climate. Of this, £11 million has been allocated to maintenance. -

Download Programme
AORTA MASTERCLASS REGISTRATION FORM www.aortamasterclass.info 03rd – 04th June 2017, London PAYMENT (check your payment method) Bank draft (Please enclose a copy) PAYMENT: Event Planet srl Branch 02020 BANK: BANCO DI NAPOLI S.p.a. IBAN: IT88 P010 1003 5151 0000 0009 082 AORTA MASTERCLASS Swift Code: IBSPITNA ROYAL BROMPTON & HAREFIELD NHS Trust Credit Card Credit Card N. Expiry Date VISA MASTERCARD DINERS CLUB Cash on site Free registration Total amount £ (Registration without payment will be not accepted) Information concerning the protection of privacy and the processing and utilization of personal data IN ACCORDANCE WITH LAW 675, PASSED ON DEC. 31 1996, WE WISH TO INFORM YOU THAT THE PERSONAL DATA YOU FURNISHED IN FILLING OUT THE REGISTRATION FORM FOR ENROLLMENT IN THIS MEETING WILL BE USED rd th EXCLUSIVELY FOR ENROLLMENT PURPOSES. IN PROCESSING THIS INFORMATION WE GUARANTEE THAT YOUR 03 - 04 JUNE 2017 PRIVACY WILL NOT BE VIOLATED AND THAT THIS DATA WILL NOT BE GIVEN OR COMMUNICATED TO THIRD PARTIES. SIGNATURE REQUIRED AORTA MASTERCLASS 2017 I have read and agree to abide by the terms and conditions enclosed IMPERIAL COLLEGE. SIR ALEXANDER FLEMING BUILDING in this registration fees form Signature Date LONDON If you are interested please fill up and scan this registration form and send it to the following email address: [email protected] or register on the website www.aortamasterclass.info FREE FOR STUDENTS AORTA MASTERCLASS PROGRAMME Saturday 03rd June 2017 DAY 1 SATURDAY 3rd JUNE 09.30 Registration, tea and coee 10.00 -

Guest Information Variety of Stores, Oxford Street Is Just a Short Bus Journey Away
LOCAL ATTRACTIONS CAMPUS MAP Hyde South Kensington Campus Royal Albert Hall Park Situated just a five-minute walk away, the Royal Albert Hall Kensington Gore Breakfast is one of the UK’s most loved and distinctive buildings, Senior Common Room Royal 07.00 - 10.30 Mon - Fri recognisable all over the world. The venue hosts more than Albert Hall 07.30 - 10.30 Sat - Sun 350 performances a year from international artists and shows including the BBC Proms each summer. The Royal Albert Hall also offers a number of guided tours for visitors. Gate Prince’s Gate s Gate ’s Gardens e’ inc ueen Pr Q Natural History Museum 44 The Natural History Museum is one of London’s architectural Prince Consort Road 3 treasures, filled with wonders from the natural world. Prince’s Gardens (North Side) 9 Science Museum Prince’s 2 Gardens The Science Museum covers all areas of science and technology 5 7 and exhibits world-class collections of scientific, technological 6 8 and medical achievements from across the globe. xhibition Road E Prince’s Gardens (Watts Way) Queen’s Lawn 1 Victoria and Albert Museum Imperial College Road The V&A is a haven for fans of art and design. It houses Science 50 metres a permanent collection of over 2.3 million objects from Museum Frankland Road South architecture, furniture, fashion, photography, ceramics and Kensington Natural History V&A much more. Museum Museum Cromwell R o a d Routes to breakfast ace Hyde Park and Marble Arch 1 Th urloe Pl Hyde Park is just a few minutes’ walk from Prince’s Gardens Thurloe Stree t and offers 350 acres of green open space in the heart of central Prince’s Gardens, Southside Halls Beit Hall (24-hour 1 4 7 Bank and ATM London. -

Stage What's On
WHAT’S ON MAIN STAGE The Hardwood Hub A series of short talks taking place throughout the day, hosted by Priya Khanchandani, Editor of ICON Magazine, Drop-In Design: MultiPly and design curator Max Fraser. 10:30–17:00 Visit Drop-in Design during the London Design Festival and 10:30 Albertopolis & Design A crucible for designing create your own structure inspired by the landmark project from the 1st to the 4th industrial revolution MultiPly in The Sackler Courtyard. Presented by the V&A. Dr Stephen Green, Senior Teaching Fellow at the Dyson School of Design Engineering looks to the area’s rich Design history The VR Box and exciting future. Bioluminescence by Jason Bruges Studio 11:00 Can Technology Change the Consciousness of a City? 10:30–17:00 Citizens aren’t data points in a passive-aggressive algorithm. Step into the darkness and be transported to the depths of the ocean Abhay Adhikari explores how we build a digitally-enabled city where the dazzling lights of bioluminescent creatures dance all around. with an abundance of empathy. This experience was developed by Jason Bruges Studio for the Natural History Museum’s current Life in the Dark exhibition. 11:30 Material Consequences: London’s Wasteline Aleksandar Stojakovic and Alexander Frehse, Studio 8FOLD founders, The Hands-on Zone discuss their installation ‘Wasteline’, presenting ways in which cities are dealing with waste, future models and architecture solutions. Roaming Collections 10:30–12.00 and 13.30–15.00 12:00 Material Consequences: From the physical to the digital See and touch specimens that have adapted to life in the dark and Materials are being recognised not only as physical objects but inspired the Natural History Museum’s current temporary exhibition. -

Together on the Frontline of the Ght with MS
PLUGGED IN Life as a blogging professor // SPLASH : Water polo and London 2012 Voyages of particle discovery ➺ KEEPING UP WITH MASCOT RIVALRIES ➺ A grand passion for aviation THE MAGA ZINE OF IMPERIAL COLLEGE LONDON Winter 2012–13 brains trust Together on the frontline of the ght with MS WELCOME | winter 2012–13 FROM THE ➜ inside issue 38 PRESIDENT & RECTOR Sta • Editor-in-Chief: Tom Miller (Biology 1995) • Creative Director: Beth Elzer Hungry for experiences that stretch them and nourish them, • Editor-at-Large and Features Imperial students go well beyond the nerd Editor: Natasha Martineau (MSc Science Communication 1994) • News Editor: Simon Watts • Managing Editors: Pamela Our 2012–13 University Agar, Saskia Daniel Challenge team jokingly referred • Sub Editor and Distribution: to the reputation of Imperial Saskia Daniel students as nerds who can x 32 Behind the scenes • Designers: Abby Lloyd-Pack, a computer but can’t appreciate BODY OF KNOWLEDGE Beth Elzer a good novel. ey went on The virtual cadaver that’s • Contributors: Elizabeth Atkin, to thrash the competition transforming anatomy training Olivia Davenport, Caroline Davis, in their rst match – their John-Paul Jones, Simon Levey, countless winning responses to 34 Going public Kerry Noble, Emily Ross-Joannou, arts and humanities questions I PROFESS Colin Smith, Elizabeth Swi, giving them the edge. Structural biologist Stephen Katie Weeks, Sam Wong (MSc Curry on life as a blogging Science Communication 2009) I’ve watched Imperial students STUDENT EXPLORERS professor tussle on the sports pitch and Over the summer members of The magazine for Imperial’s sing enchantingly in the Royal Imperial College Caving Club 37 Travel friends, supporters and alumni, Albert Hall and am continually helped discover Slovenia’s President & 18 Feature CERN COURIER including former students of in awe of their wide-ranging longest cave system.