THE RESPONSE of SMALL CRAFT to WAVE ACTION by M
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Spring 2000-A Snips
Spring 2000 The Trailer Sailors Association Notes and Announcements 2 Trailer/Sailor s Association Information . ... ... 2 President s column ... .... .Wayne Bell 2 Errata from past issues . ... 3 North Channel Cruise Announcement ... .John Clement 3 Note on Priority Mail ..David Craigie 4 Treasurer s Report ... David Craigie 4 Flags and Tee Shirts Announcement .. 5 Trailer Sailor Web Discussion Board ...John Coppedge 5 Trailer Sailors Need Help in Florida ...David Craigie How-to Articles 6 Gizmos, Gadgets, and Galley ...ed. Debbie Bell 7 Think Alcohol Stoves are Hazard-Free? ....Ray R. Davidson 7 Cushion Tip ..Bob Brennan 8 Managing Your H2O While Cruising ..David Craigie Cruising Articles 9 Before I Get Old ... ....Rita Thomas 10 Cruising with George and George ...Larry McComb 12 The Diagonal Alternative ...Bill Atkins 15 Things to do In, On, and Around Lake Erie ..Alan Reichert 16 Summer 1998 Around Lake Huron (almost)-Part 2 ...Henk Vanderhulst 19 Pacific Coast Cruising Adventure Aboard our Bayfield 25 .Rod & Karen Duncan 20 Three Swans in the Pacific Northwest ....Carol Kulish 25 Lake Superior Cruise 1999 .Jack Johnson 27 Charleston, SC to Savannah, GA via the ICW .Max & Mandy Miller 31 McGregor Bay ..Wayne Bell 34 A Fall Cruise of the Southern Chesapeake . ...Guy Hubbard 33 Classified Ad . 38 Cruise and Gathering Announcements .. 39 Editor s Last Word ... ..Mike Nelson 40 Membership Application ... The authors of the newsletter disclaim any and all responsibility for any kind of injury or damages sustained which may result from the application of any or all ideas or suggestions appearing in any articles of Clipper Snips. -

Clipper Snips
Clipper Snips The magazine of the Trailer/Sailors Association Trailer/Sailors Association www.trailersailors.org Summer/Fall 2010 2 Presidents Column Mike Nelson Articles 12 Pizza On Your Boat Mike Nelson & Irene Clement 13 Sailabration 2010 John Clement 17 I’m Glad I’m a Moron Rebecca and Bob Bringle 21 De-Rigged & Ready to Go, But It’s Late Irene Clement 22 Ramp Report— Annapolis Maryland John Ulmer Cruises 3 Spring 2010 Cruise Bryan Childs & Bob Harris 6 Extended Cruising on a Small Boat Laurence Wright 25 What’s in a Name Larry Dale Other Stuff 11 Sailors Quiz Marjorie Whites 20 Tips and Tricks Diana Nelson T/SA Tee-shirts For T/SA Hats ($13US) T/SA Wear Flags ($16US), Temporarily unavailable contact: David Craigie at for sale [email protected] 1 challenge in upcoming years. Notes from the As of this date, I have received only 4 responses to my posting on our TrailSail discussion group about an President annual meeting. Those responders said they would Mike Nelson only attend a meeting if it were within an hour or two of their homes. No decision has yet been made, but if As I write this, another summer draws to a close, al- the interest level in an annual meeting remains low, it though the calendar says we still have some summer probably will not be held this year. left. I hope you all have had good sailing times. Webmaster Chris Holderness has suggested we move The 2010 North Channel cruise, as well as the Early our web site to a different technical platform. -
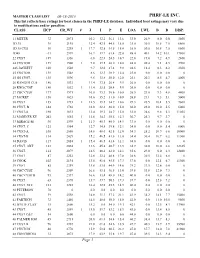
PHRF-LE INC. This List Reflects Base Ratings for Boat Classes in the PHRF-LE Database
MASTER CLASS LIST 06-18-2015 PHRF-LE INC. This list reflects base ratings for boat classes in the PHRF-LE database. Individual boat ratings may vary due to modifications and/or penalties. CLASS HCP CR_WT # J I P E LOA LWL B D DISP. 11 METER 72 2071 10.2 32.2 36.1 13.6 33.0 26.9 8.0 0.0 3600 1D 35 30 2195 12.4 42.5 44.5 18.0 35.0 30.5 10.8 7.5 6600 1D 35 CUS 30 2248 1 17.7 42.5 44.5 18.0 35.0 30.5 10.8 7.5 6600 1D48 -33 2939 16.7 57.7 61.4 22.0 48.0 40.1 14.2 10.1 17860 22 CUST 189 1356 6.8 22.8 24.5 10.7 22.0 19.0 7.2 4.9 2100 24 CUSTOM 159 1500 1 9.8 29.5 28.0 10.0 24.0 20.4 9.1 4.5 2900 245 JACKETT 168 1503 9.7 32.0 27.4 9.8 24.5 18.4 8.3 4.2 3300 25 CUSTOM 159 1548 8.6 32.3 30.9 12.4 25.0 0.0 0.0 0.0 0 25 GS CUST. 135 1596 9.6 33.8 30.0 12.0 25.1 20.3 8.5 4.7 4000 26 RANGER CUS 186 1532 11.4 33.5 26.4 9.9 26.0 0.0 0.0 0.0 0 26 RNG.CUST 186 1532 1 11.4 33.5 26.4 9.9 26.0 0.0 0.0 0.0 0 27 C&C CUST 177 1571 10.0 35.3 30.6 10.8 26.5 23.0 9.3 4.8 4400 27 JACKET 156 1623 10.6 35.2 31.0 10.8 26.8 21.1 9.3 5.1 5000 30 CUST 153 1733 1 12.5 39.5 34.7 10.6 29.3 23.5 10.1 5.5 7600 30 CUST. -

Luff Letter Editor
October 2009 Autumn arrived on September 22. We all Bob Paterson, a club member, has been know what that means. Not just football contracted to remove several dead trees. in Tennessee but cooler temperatures and Several new pylons will be installed on the return of steady breezes. It also means Dave’s and the West docks. time to get your work hours before the The Long Range Planning Committee end of the year. Following is a list of pro- and sub-committees are finalizing the pro- jects to help you complete your work hour posal for a new west dock system. Details requirements while improving the clubs will be available in the near future. The appearance. Hurry, now’s your chance! plans for a mast hoist/ladder system to as- Work cards will be tallied November 15th. sist members for making repairs to their This past spring we were rained out on masts without removing it are still in the one “official work Saturday”. As a result design stage. Details will be available in several projects were not completed. To- the near future. wards the end of the week of October 5th, PLEASE TURN OFF ALL LIGHTS, AP- a large dumpster will be located near the PLIANCES AND FANS AND LOCK west ramp. This is for depositing all the THE DOORS BEFORE YOU LEAVE shoreline debris that has accumulated over THE BUILDINGS. the summer from the rain swollen river and all the shrub cuttings from work pro- As always, if you have any concerns or re- jects. Members are asked to pick a project pairs to be made, that meets their ability. -

Page 1 of 13 S=SPORT BOAT GYA PHRF RATING LIST CF=CRUISER
Page 1 of 13 S=SPORT BOAT GYA PHRF RATING LIST CONTACT: Tom Beery, 1001 Sea Cove, Pascagoula, MS 39581 CF=CRUISER FURLING RUN AS OF MARCH 21, 2014 TEL: 228-769-6718, CELL: 228-617-6536, e-mail: [email protected] (sorted by YACHT TYPE, SAIL NUMBER) DIST. SPNK TEMPLATE RECORDED XPHRF CLASS- EXPIRATION USSA CERT CREW NET RACES IN CERT. IFICATION YACHT TYPE YACHT NAME OWNERS FIRST NAME LAST NAME DATE SAIL # MEMB # # LIMIT CLUB RATING N. MILES CF ALBERG 30,RF RESOLUTE CHARLES(CHUCK) W. THOMAS 2/14/2015 525 3788 8 CSA 246 ALERION EXPRESS 28 EVELYN KENNETH D. WALL 4/14/2015 5 3421 7 PTYC 180 10.52 S ANTRIM 27 ODR ANEMONE TICKLER ANTHONY HUDSON 3/31/2015 14 3803 7 NOYC 93 5.89 ARTEKNO H-35 HOLLY II BILL CULBERSON 3/21/2015 26 N/A 353 9 BUCYC 168 64.34 ATKIN'S 39 CUSTON YAWLDESTINY JAMES F. CASH 5/1/2015 3921 11 SBYRC 216 B-25 PIRANHA ANDREW S AND DAWN NOLTE 5/23/2014 32 138690f 194 6 GYC 129 1014.19 S B-32 DEFIANCE RYAN BANCROFT 4/5/2014 46410 183498G 3463 9 NOYC 66 321.07 BAVARIA B/ONE ERIC NELSON 5/1/2015 17 3934 6 PELYC 117 BAYFIELD 25 OVERTIME KENNETH JOSEPH HOPEL JR. 2014/04/31 235 3871 6 NONE 291 CF BENETEAU 305 SD,RF WITCH DOCTOR NICK HAJDU 3/24/2016 686 3855 8 NOYC 180 93.59 CF BENETEAU 31,RF MICKEY-DEE MICHAEL J. LAGARDE 5/20/2015 23 3676 9 FWYC 207 CF BENETEAU 323,RF CA VA JAMES LANDIS 4/1/2015 3924 9 SYC 201 CF BENETEAU 323,RF PAPILLON RICHARD C. -

Handicaps CVSYC Saison 2021 Révision : 05 Date : 29 Juin 2021
Handicaps CVSYC Saison 2021 Révision :05 Date : 29 juin 2021 Entrée des données (cases blanches seulement) No. Voile Voilier No Voile Propriétaire Type de voilier Club Lac SPI Code SPI T/T SPI T/D VB VB T/T VB T/D Classe HDCP Ajust. CVSYC CVSYC CVSYC CVSYC Jauge Ajustem Ajustem utilisé suggéré Code (base, CVSYC SPI T/T SPI T/D VB T/T VB T/D Std ents ents mess, (extrait totaux totaux OD, autom Spi VB ODF, de ODE, HDCP&D etc) IM) Changementcette année Changementcette révision Allegro GARNEAU, Jocelyn CVSYCD-M4555 #N/A #N/A 4B55 #N/A #N/A #N/A 115% #N/A #N/A #N/A #N/A #N/A 3 21 381 Amarys 381 BOURSIER, Pierre CATALINA 28-2 WK CVSYC D-M 2544 0,958 216 2C44 0,936 237 VB(2) 100% 0,958 216 0,936 237 198 18 39 1570 Amistad LEBEAU, René Bénéteau First 26 CVSYC D-M L515 0,993 186 LA15 0,975 201 VB(3) 115% 0,962 213 0,942 231 195 -9 6 617 Andante 617 CALMELS, Marjolaine C+C 25-2 CVSYC D-M 455M 0,952 222 4B5M 0,933 240 VB(3) 100% 0,952 222 0,933 240 219 3 21 Andiamo ASSELIN, Denis CATALINA 25-1 CVSYC D-M357M 0,945 228 3C7M 0,923 249 VB(3) 115% 0,910 262 0,887 286 228 0 21 413 Aponivi COULOMBE, Simon C&C 25 MK I CVSYC D-M 356M 0,936 237 3C6M 0,914 258 VB(2) 115% 0,900 272 0,877 296 234 3 24 25 Aquavita 081 BOSSÉ, Bertrand NIAGARA 26-1 CVSYC D-M 454M 0,989 189 4B4M 0,968 207 VB(2) 100% 0,989 189 0,968 207 183 6 24 Century 21 Aquilon CLÉROUX, Lyne C+C 25-1 CVSYC D-M 444M 0,942 231 4B4M 0,926 246 VB(3) 100% 0,942 231 0,926 246 222 9 24 Azul 107 GÉLINAS, Philippe C+C NIAGARA 24-1 CVSYC D-M 434M 0,936 237 4B4M 0,920 252 VB(3) 100% 0,936 237 0,920 252 228 -

AKA List of Boat Class Version for SP List
9/14/2011 CLASS VERSION LIST (aka) Page 1 of 10 BOLD items are boats in PHRF-LO database THIS BOAT WITH/IS A VERSION OF IS A VERSION OF OR KNOWN AS ALDEN 45 EXTENDED STERN ALDEN 43 ALDEN 48 EXT STERN ALDEN 46 ALDEN 50 EXT STERN ALDEN 46/48 ALDEN 54 EXTENDED STERN, KETCH ALDEN 50/52 ALLIED 3030 AKA CHANCE 3030 ALLIED 39 SKEG RUDDER,NEW TRANSOM BORSAW 40/OWENS 40 ALLMAND 35 AKA CAPTIVA 35 ALOHA 8.2 AKA ALOHA 27 ANNAPOLIS 35 AKA YOUNG SUN 35 ANNAPOLIS 44 SLOOP LUDERS 44 ANTIGUA 44 AKA CSY 44 WALK-THROUGH ANTIGUA 53 UPDATED MORGAN OI51 APHRODITE 101 AKA BIANCA 101 APHRODITE 101 AKA INTERNATIONAL 101 AQUARIUS 23 AKA BALBOA 23 AQUARIUS 23-2 KEEL AQUARIUS 23 AQUARIUS 7.0 MASTHEAD,OUTBOARD RUDDER AQUARIUS 23 ARCO 33 Renamed COLUMBIA 33 ATLANTIC 44 AKA Jeanneau SO/Sun Magic 44 AURA 10.7 AKA COLUMBIA 10.7 AURA 8.7 AKA COLUMBIA 8.7 AURA H35 AKA HUGHES 35 AURA H40 AKA HUGHES 40 BABA 40 AKA PANDA 40 BAHAMA 26 AKA ISLANDER 26 BAHAMA 28 AKA ISLANDER 28 BAHAMA 30 NEW KEEL,RUDDER, AND DECK ISLANDER 30-2 TM BALBOA 23 AKA AQUARIUS 23 BALBOA 8.2 AKA BALBOA 27 BALT Family 17 AKA Jeanneau Sun Fast 17 BALTIC 33 SAIL DRIVE,TEAK DK OVERLAY,NEW KEEL C+C 33 BAYFIELD 25 AKA BAYFIELD 2325 BAYFIELD 32 AKA BAYFIELD 3032 BAYFIELD 32C TALL RIG, BOW SPRIT BAYFIELD 32 BBM IMS 39 IMSized PETERSON 38 BENETEAU 305 MORE FREEBOARD,MODIFIED STERN BENETEAU 30E BENETEAU 30ES IOR SKIRT STERN,LEAD KEEL,FRAC RIG BENETEAU 30E BENETEAU 325 MORE FREEBOARD,MODIFIED STERN BENETEAU 32 BENETEAU 46 AKA BENETEAU 461 BENETEAU EVASION 28 PILOT HOUSE BENETEAU ESCAPADE 28 BENETEAU IDYLLE 1150 -
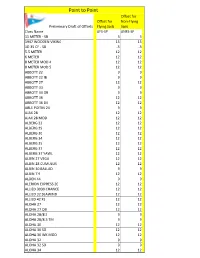
Copy of P2P Ratings for Release Dr Mod.Xlsx
Point to Point Offset for Offset for Non-Flying Preliminary Draft of Offsets Flying Sails Sails Class Name ΔFS-SP ΔNFS-SP 11 METER - SB 3 3 1947 WOODEN VIKING 15 15 1D 35 CF - SB -3 -3 5.5 METER 12 12 6 METER 12 12 8 METER MOD 4 12 12 8 METER MOD 5 12 12 ABBOTT 22 9 9 ABBOTT 22 IB 9 9 ABBOTT 27 12 12 ABBOTT 33 9 9 ABBOTT 33 OB 9 9 ABBOTT 36 12 12 ABBOTT 36 DK 12 12 ABLE POITIN 24 9 9 AJAX 28 12 12 AJAX 28 MOD 12 12 ALBERG 22 12 12 ALBERG 29 12 12 ALBERG 30 12 12 ALBERG 34 12 12 ALBERG 35 12 12 ALBERG 37 12 12 ALBERG 37 YAWL 12 12 ALBIN 27 VEGA 12 12 ALBIN 28 CUMULUS 12 12 ALBIN 30 BALLAD 9 9 ALBIN 7.9 12 12 ALDEN 44 9 9 ALERION EXPRESS 20 12 12 ALLIED 3030 CHANCE 12 12 ALLIED 32 SEAWIND 12 12 ALLIED 42 XL 12 12 ALOHA 27 12 12 ALOHA 27 OB 12 12 ALOHA 28/8.5 9 9 ALOHA 28/8.5 TM 9 9 ALOHA 30 12 12 ALOHA 30 SD 12 12 ALOHA 30 WK MOD 12 12 ALOHA 32 9 9 ALOHA 32 SD 9 9 ALOHA 34 12 12 Point to Point Offset for Offset for Non-Flying Preliminary Draft of Offsets Flying Sails Sails Class Name ΔFS-SP ΔNFS-SP ALOHA 8.2 12 12 ALOHA 8.2 OB 12 12 AMF 2100 12 12 ANCOM 23 12 12 ANDREWS 30 CUS 1 L30 9 9 ANDREWS 30 CUS 2 L30 9 9 ANDREWS 30 CUS 3 L30 9 9 ANDREWS 30 CUS 4 L30 9 9 ANDREWS 30 CUS 5 L30 9 9 ANDREWS 30 CUS 6 L30 9 9 ANDREWS 30 CUS 7 L30 9 9 ANTRIM 27 IB - SB -9 -9 ANTRIM 27 OB - SB -9 -9 APHRODITE 101 9 9 AQUARIUS 23 9 9 ARCHAMBAULT 31 6 6 ARCHAMBAULT 35 CF 3 3 ARCHAMBAULT 40RC CF MOD 3 3 ATLANTIC 12 12 AURORA 40 KCB 9 9 AVANCE 36 12 12 B 25 -SB 3 3 B 32 OB MOD -SB -3 -3 BALATON 31 12 12 BALBOA 26 SK 9 9 BALTIC 42 C&C 9 9 BALTIC 42 DP 9 9 BANNER -

SLVYRA List of Rated Yachts As of August 15Th 2019 Liste ARVSL Des Voiliers Mesurés En Date Du 15 Aout 2019
SLVYRA list of rated yachts as of August 15th 2019 Liste ARVSL des voiliers mesurés en date du 15 Aout 2019 NO. NOM/NAME TYPE CLUB LAC CODE SPI T/T T/D CODE VB T/T T/D CLAS. HDCP 0 SOLACE ALBERG 22-1 RO O 555K 0.891 282 5B5K 0.874 300 VB(3) base 0 DIANA ALBERG 29-1 ZZ S553 0.929 243 SC53 0.908 264 VB(2) base 0 TRAIL WIND ALBERG 29-1 ZZ 5555 0.945 228 5B55 0.926 246 VB(2) base 0 L'ADDITION ALBIN VEGA 27-1 PC StL(1) 5555 0.926 246 5B55 0.908 264 VB(2) base 0 REAL ESCAPE ALBIN VEGA 27-1 B StL(1) 5555 0.926 246 5B55 0.908 264 VB(2) base 0 COOL SEAS (226) ALBIN VEGA 27-1 ZZ 5555 0.926 246 5B55 0.908 264 VB(2) base 0 REYKJAVIK 2 ALOHA 8.2/27-1 L D-M 5555 0.962 213 5B55 0.942 231 VB(2) base 0 THALASSA (073) ALOHA 8.2/27-1 B StL(1) 5555 0.962 213 5B55 0.942 231 VB(2) base 0 WANDERLUST ALOHA 8.5/28-1 B StL(1) 5555 0.982 195 5B55 0.962 213 VB(2) base 0 SHE CAT ALOHA 8.5/28-1 RO O 3555 0.975 201 3B55 0.955 219 VB(2) mes. 0 CIAO ALOHA 8.5/28-1 SF StF 5555 0.982 195 5B55 0.962 213 2 base 0 SHANGRILA ALOHA 8.5/28-1 SF StF 5555 0.982 195 5B55 0.962 213 VB(2) base 0 LA PIAULE 2 ANNAPOLIS 26-1 S D-M 457M 0.955 219 4B7M 0.936 237 VB(3) base 0 ZEN BAYFIELD 25-1 S D-M 2543 0.885 288 2C43 0.865 309 VB(3) mes. -

United States Sailing Association Your Passion. Organized. HISTORY OF
United States Sailing Association Your Passion. Organized. HISTORY OF US PHRF® AFFILIATED HANDICAPS 2016 PHRF® is a Registered Trademark of the United States Sailing Association Copyright 2016 United States Sailing Association Box 1260, Portsmouth, RI 02871 www.ussailing.org (401) 683-0800 FAX (401)683-0840 THE UNITED STATES PERFORMANCE HANDICAP RACING FLEET The United States Performance Handicap Racing Fleet (USPHRF) is an empirical handicapping rule administered by a technical rule committee of US Sailing. The USPHRF Committee promotes performance handicap racing for monohull and multihull sail boats applying the PHRF rule. The Committee researches, develops, and distributes guidelines for performance handicapping using systematically applied empirical methodology to determine estimates of speed potential. PHRF Committee Position Address Phone Type Bingman, Bruce Chair 498 Sara Dr. 1 (410) 280-2309 Home Annapolis, MD, 21401 1 (703) 801-4388 Mobile 1 (202) 781-5932 Work Ansfield PhD, Paul J. Vice Chair 1135 Maricopa Dr 1 (920) 233-5782 Fax Oshkosh, WI, 54904-8118 1 (920) 233-5743 Home 1 (920) 312-8185 Mobile Barnes, Tom Member at Large 12470 Country Club Drive 1 (231) 547-5137 Home Charlevoix, MI, 49720 1 (231) 547-1473 Work Bottino MD, Gino C. Member at Large 215 Courtland Ave 1 (914) 646-9200 Mobile Stamford, CT, 06906 1 (914) 241-8866 Work Collins, John J Member at Large 23 Pilgrim Rd 1 (781) 639-1648 Home Marblehead, MA, 01945-1710 Kellner, Bill Member at Large 32331 Stoney Brook Dr 1 (440) 933-9917 Fax Avon Lake, OH, 44012-2136 1 (440) 667-3732 Mobile Kendrick, June Member at Large 11 Anthony Ct 1 (631) 549-4810 Huntington, NY, 11743-1327 1 (631) 673-5781 Home Plant, Robert H Member at Large Stauber, Keith J Member at Large 4139 S Lake Avenue 1 (218) 722-6255 Home Duluth, MN, 55802-2551 1 (218) 390-1776 Mobile Tichenor, James H Member at Large 3827 Del Monte Dr. -

Good Old Boat Articles by Category
Good Old Boat articles by category Feature boats Cape Dory 30, Number 1, June 1998 Ericson 35, Number 2, Sept. 1998 Niagara 35, Number 3, Nov. 1998 Blackwatch 19, Number 4, Jan. 1999 Baba 30, Number 5, Mar. 1999 Pearson Commander/Ariel, Number 6, May 1999 Block Island 40, Number 7, July 1999 Nicholson 35, Number 8, Sept. 1999 Bayfield 40, Number 9, Nov. 1999 C&C Redwing 30, Number 10, Jan. 2000 Tanzer 22, Number 11, Mar. 2000 Morgan 38, Number 12, May 2000 Classic sailboats (Bermuda 40, Valiant 40, Cherubini 44), Number 12, May 2000 West Wight Potter, Number 13, July 2000 Allied Seabreeze, Number 14, Sept. 2000 Ericson 36C, Number 15, Nov. 2000 Seven Bells (part 1), Number 15, Nov. 2000 Seven Bells (part 2), Number 16, Jan. 2001 Catalina 22, Number 17, Mar. 2001 Cheoy Lee Offshore 40, Number 18, May 2001 Lord Nelson 35, Number 19, July 2001 Tartan 33, Number 20, Sept. 2001 Stone Horse, Number 22, Jan. 2002 Sea Sprite 34, Number 23, Mar. 2002 Sabre 30, Number 24, May 2002 Columbia 28, Number 25, July 2002 Cheoy Lee 35, Number 26, Sept. 2002 Nor'Sea 27, Number 27, Nov. 2002 Allied Seawind 30, Number 28, Jan. 2003 Bristol 24, Number 29, Mar. 2003 Montgomery 23, Number 30, May 2003 Victoria 18, Number 31, July 2003 Bristol 35.5 Number 32, September, 2003 Eastward Ho 31, Number 33, November, 2003 Ericson 29, Number 34, January 2004 Watkins 29, Number 36, May 2004 Spencer 35, Number 38, September 2004 Pacific Seacraft/Crealock 37, Number 39, November 2004 Cheoy Lee 32, Number 40, January 2005 Tayana 37, Number 41, March 2005 Bristol 29.9, Number 43, July 2005 Cape Dory 25, Number 45, November 2005 Lazy Jack 32, Number 46, January 2006 Alberg 30, Number 47, March 2006 Ranger 28, Number 50, September 2006 Allegra 24, Number 51, November 2006 Finisterre's sister, Number 52, January 2007 Islander 30, Number 53, March 2007 Review boats Albin Vega, Number 5, March 1999 Bristol Channel Cutter, Number 6, May 1999 Cal 20, Number 7, July 1999 Contessa 26, Number 8, Sept. -
Features 17 10 STEPS to a PERFECT PAINT JOB Columns Often the Only Solution to Repair Dull and 11 ELECTRONICS Faded Gelcoat on an Older Fiberglass Boat Is to Paint It
– 2002 issue #2 – Features 17 10 STEPS TO A PERFECT PAINT JOB Columns Often the only solution to repair dull and 11 ELECTRONICS faded gelcoat on an older fiberglass boat is to paint it. While you can do this yourself, a The Weak Link: Fuses and circuit breakers prevent too much amperage from professional touch guarantees spectacular traveling through a wire, building heat results. through resistance that may damage electri- By Nick Bailey cal and electronic equipment, and more important, cause an electrical fire. Here’s how to properly install adequately sized cir- 27 CORROSION 101 cuit protection devices. — By Kevin Jeffrey This segment in our corrosion series looks at stain- 21 PROJECTS less steel, an alloy that, contrary to popular belief, Need More Gauges?; Happiness Is Fewer does rust under certain conditions, sometimes to Holes; Anchor Locker Ventilation; Oil Pump the point of total failure. Storage. By Susan Canfield 34 SAILBOAT RIGGING Don’t Be Foiled By Foils: 30 THRUSTER FAQ Centerboards, swing or lifting keels are often overlooked components on sailboats. Some things you should know about Carefree operation requires this equipment choosing, installing, operating and be inspected and maintained during every maintaining bow and stern thrusters. haulout. Here’s how to remove, repair and reinstall. — By Nick Bailey 47 POWERBOAT RIGGING 39 BUYING RIGHT Stern Drive Alignment: The A Surveyor’s Perspective. There are some engine, transom assembly and sterndrive of your engine must be in perfect alignment to great buys on used boats if you know what to prevent major engine damage. To align look for.