DOCSLIB.ORG

Cosmological Nucleosynthesis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cosmological Nucleosynthesis Cosmology Cosmological Nucleosynthesis v In the discussion of the thermal history of the early universe form temperatures 1011 ◦K down to about 106 ◦K we were neglecting the tiny contribution of relict nucleons which were not completely annihilated in particle-antiparticle annihilation. v Nucleons, the building blocks of atomic nuclei, were formed abundantly in the QCD phase transition out of the quark-gluon plasma at temperatures T ∼ 150 MeV corresponding to a temperature T ∼ 2 × 1012 ◦K and cosmic time t ∼ 20µs. v The QCD phase transition sets in after the annihilation of the heavier quarks (t; b; c) during the annihilation of s quarks. During the QCD phase transition color neutral SU(3)c triplet states form, the baryons, as well as anti-triplets representing the antibaryons together with quark–antiquark singlets, the mesons. The lightest hadrons are the nucleons (N), proton (p) and neutron (n), and their antiparticles (spin 1/2 fermions), which when formed are non-relativistic (essentially at rest) and the lightest mesons, the pions π± and π0 (spin 0 bosons). c 2009, F. Jegerlehner nx Lect. 9 xo 138 Cosmology v Baryon–antibaryon annihilation immediately sets in during their formation. Here the mystery of the baryon asymmetry plays the key role for the future evolution, namely, the annihilation turned out to be incomplete with a relict −10 −9 η = nN(t0)=nγ(t0) ∼ 10 − 10 of surviving baryons. The only particles left in large numbers at this time were pions, muons, electrons, neutrinos and photons. After baryon–antibaryon annihilation, for T < 10 MeV, the total number of baryons nB = nN − nN¯ = np − np¯ + nn − nn¯, in practice nB = np + nn since now nN¯ nN, remains conserved due to baryon number conservation. Baryons are free protons, free neutrons or protons and neutrons bound in nuclei. While nuclear strong interaction forces bind nucleons in nuclei weak interactions convert neutron and protons into each other. r As we will see, about one quarter of all nucleons form nuclei (A > 1), with about an equal amount of neutrons and protons, while approximately three quarters remain free protons. c 2009, F. Jegerlehner nx Lect. 9 xo 139 Cosmology + − r Later, when T < 10 keV, after e e –annihilation, we also will have ne+ ne− and ne− = np, where np represents all protons, the free ones as well as the ones bound in nuclei (presumed charge neutrality of the universe). r Radiation and matter (electron, protons and nuclei) remain in thermal equilibrium as long as there are lots of free electrons. After e+e−–annihilation, atoms in particular hydrogen may form e− + p H + γ and essentially, when Tγ < 13:6 eV, the ionization energy of hydrogen, electrons will have been trapped by protons and nuclei ions (recombination). The universe becomes transparent and photons decouple from matter. More details on that later. We are now discussing the evolution of the relict densities of baryons and the formation of light nuclei. Relevant basic processes: c 2009, F. Jegerlehner nx Lect. 9 xo 140 Cosmology n + ν p + e− ; n + e+ p + ν¯ ; n p + e− + ν¯ v ν ≡ νe, other neutrinos inactive here. v kB T mN ! nucleons at rest (non-relativistic) v Q–value: Q = mn − mp ' 1:293 MeV − Q = Ee − Eν n + ν p + e + Q = Eν − Ee n + e p + ν¯ − Q = Eν + Ee n p + e + ν¯ Calculation of rate: r cross-section: weak 2–body reaction n + e ! p + ν¯ 2 2 2 2π2~3 AE2 G (1+3 g ) cos θC σ = ν ; A = F A ve 2π3 ~ c 2009, F. Jegerlehner nx Lect. 9 xo 141 Cosmology −5 −2 GF = 1:16637(1) × 10 GeV Fermi constant gA = 1:257 nucleon axial vector coupling of β-decay cos θC = 0:9745(6) , ΘC Cabibbo mixing angle ve the electron velocity Electrons and neutrinos are relativistic ! have to take into account Fermi distribution (Pauli-Principle): r number density of electrons (with momentum between pe and pe + dpe) 2 4 π pe dpe exp (E =k T) + 1 −1 (2 π ~)3 e B c 2009, F. Jegerlehner nx Lect. 9 xo 142 Cosmology r fraction of unfilled antineutrino levels: −1 −1 1 − exp (Eν=kBTν) + 1 = exp (−Eν=kBTν) + 1 such that the total rate reads 1 + R 2 2 −1 −1 λ(n + e ! p + ν¯) = A Eν pe dpe exp (Ee=kBT) + 1 × exp (−Eν=kBTν) + 1 0 changing variable to q ≡ −Eν = −Q − Ee yields an integral over q + v from q = −∞ to q = −Q − me for n + e ! p + ν¯ − v from q = −Q + me to q = 0 for n ! p + e + ν¯ v from q = 0 to q = +1 for n + ν ! p + e− while the integrand is unchanged. The total rate of disappearance of neutrons then is given by c 2009, F. Jegerlehner nx Lect. 9 xo 143 Cosmology +1 r R m2 (Q+q)2 q2 dq λ(n ! p) = = 1 − e (Q+q)2 1+eq=kBTν 1+e−(Q+q)=kBT −∞ with a gap from q = −Q − me to q = −Q + me in the integration range (unphysical region). Similarly, one calculates the total rate of production of neutrons to be +1 r R m2 (Q+q)2 q2 dq λ(p ! n) = = 1 − e (Q+q)2 1+e−q=kBTν 1+e(Q+q)=kBT −∞ again, with a gap from q = −Q − me to q = −Q + me in the integration range. This allows us to calculate the fraction of neutrons among the nucleons, by solving the differential equation dXn dt = −λ(n ! p) Xn + λ(p ! n) (1 − Xn) c 2009, F. Jegerlehner nx Lect. 9 xo 144 Cosmology with appropriate initial conditions. Initial Condition One can check (Exercise) that for fixed time–independent temperature T = Tν the two rates λ(p ! n) and λ(n ! p) have a ratio λ(p!n) λ(n!p) = exp (−Q=kBT) for T = Tν which would imply a time–independent solution c 2009, F. Jegerlehner nx Lect. 9 xo 145 Cosmology Xn = Xn = exp (−Q=k T) ; Xp 1−Xn B the non-relativistic equilibrium distribution. Thus what keeps this ratio away from equilibrium is the inequality of T and Tν and the fact that they depend on time. When baryons are produced during the QCD–phase transition we have kBT Q and we can calculate the integrals by setting T = Tν and Q; me = 0, such that +1 Z q4 dq λ(n ! p) = λ(p ! n) = A 1 + eq=kBT 1 + e−q=kBT −∞ 7 T 5 = π4 A (k T)5 = 0:400 sec−1 15 B 1010 ◦K which is > 1 for T > 1:22 × 1010 ◦K . c 2009, F. Jegerlehner nx Lect. 9 xo 146 Cosmology Thermal equilibrium means dXn λ(p!n) 1 = 0 , Xn = , Xn = dt λ(p!n)+λ(n!p) (1+exp(Q=kBT)) Crucially important is that the equilibrium value is established at high enough temperatures when the electron chemical potential is zero (still large numbers of electrons and positrons) such that no assumption about the initial proton/neutron ratio is necessary! This is expected to be satisfied for T > 3 × 1010 ◦K and we may solve our exact equation for Xn with this boundary condition. The solution can be obtained numerically; see the Table c 2009, F. Jegerlehner nx Lect. 9 xo 147 Cosmology ◦ T( K) t(sec) Xn 1 × 1012 0:0001 0:4962 3 × 1011 0:0011 0:4875 1 × 1011 0:0099 0:4626 3 × 1010 0:1106 0:3798 1 × 1010 1:008 0:2386 3 × 109 12:67 0:1654 1:3 × 109 91:09 0:1458 1:2 × 109 110:2 0:1425 1:1 × 109 135:1 0:1385 1 × 109 168:1 0:1333 9 × 108 2:12:7 0:1268 8 × 108 274:3 0:1182 7 × 108 362:6 0:1070 6 × 108 496:3 0:0919 3 × 108 1980 0:0172 1 × 108 17780 3:07 × 10−10 c 2009, F. Jegerlehner nx Lect. 9 xo 148 Cosmology Given the rate λ, the maximum number of collisions can be found by multiplying the rate with the Hubble time H = 1=2t. Earlier, we calculated s !2 3 1 1010 ◦K t = + const = 0:994 sec + const 16πGag∗ T 2 T 3 such that, with g∗ = 43=4, λ/H ' 0:8 × T which is > 1 for 1010 ◦K T > 1:1 × 1010 ◦K . Because of the T 3 behavior the rate drops fast and equilibrium is lost quickly between 3 × 1010 ◦K and 1010 ◦K . Little later all but neutron β–decay plays a role in proton– neutron transmutation, also due to the fact that electron and positron densities rapidly decrease because of e+e−–annihilation. Then the decrease of Xn just follows neutron decay. Exercise: Show that Xn ! 0:1609 exp (−t/τn) with τn = 885:7 sec is the neutron lifetime. The above would be the story if nucleons would not get bound into nuclei where also neutrons get stable. c 2009, F. Jegerlehner nx Lect. 9 xo 149 Cosmology Nuclei if in Equilibrium We are interested here in what happens after temperatures have dropped way below the proton mass T mp such that all nucleons and nuclei are non-relativistic. In thermal equilibrium we then have (see Exercise at end of previous lecture) m T 3=2 µi−mi i T ni = gi 2π e for the number densities of proton (i = p), neutron (i = n) or a nuclei of type i = (Ai − Zi) n + Zi p. If nuclear reaction rates for the formation of a nucleus (Ai − Zi) n + Zi p i from protons and neutrons would be sufficiently high to maintain chemical equilibrium, we would have µi = (Ai − Zi) µn + Zi µp c 2009, F.
Load more

Recommended publications
  • Concepts for a Deuterium-Deuterium Fusion Reactor
    Concepts for a deuterium-deuterium fusion reactor Roberto Onofrio1, 2 1Dipartimento di Fisica e Astronomia “Galileo Galilei”, Universit`adi Padova, Via Marzolo 8, Padova 35131, Italy 2Department of Physics and Astronomy, Dartmouth College, 6127 Wilder Laboratory, Hanover, NH 03755, USA We revisit the assumption that reactors based on deuterium-deuterium (D-D) fusion processes have to be necessarily developed after the successful completion of experiments and demonstrations for deuterium-tritium (D-T) fusion reactors. Two possible mechanisms for enhancing the reactivity are discussed. Hard tails in the energy distribution of the nuclei, through the so-called κ-distribution, allow to boost the number of energetic nuclei available for fusion reactions. At higher temperatures − − than usually considered in D-T plasmas, vacuum polarization effects from real e+e and µ+µ pairs may provide further speed-up due to their contribution to screening of the Coulomb barrier. Furthermore, the energy collection system can benefit from the absence of the lithium blanket, both in simplicity and compactness. The usual thermal cycle can be bypassed with comparable efficiency levels using hadronic calorimetry and third-generation photovoltaic cells, possibly allowing to extend the use of fusion reactors to broader contexts, most notably maritime transport. I. INTRODUCTION high yield scintillating materials and hadronic calorime- try with third-generation photovoltaic cells. This could lead to energy conversion at an initially nearly compara- It is usually assumed that the first commercial fusion ble efficiency with respect to a thermal cycle, with un- reactors will be based on D-T mixtures, and within this known margins for improvement, and within a compact frame a well-defined path has been paved with the ongo- design.
    [Show full text]
  • Can Deuterium Formation Be Measured?
    CAN DEUTERIUM FORMATION BE MEASURED? Robert K. Soberman∗ and Maurice Dubin† retired (Dated: November 12, 2018) The fundamental PP reaction has never been attempted in the laboratory as theory states it cannot be measured within the human life span. This forms the foundation of stellar nucleosynthesis and the standard solar model. Yet numerous observations including the Sun’s obvious variability argue the theory is flawed and the reaction occurs in times many orders of magnitude shorter than prediction. Considering the consequence to accepted models and controlled fusion, testing is warranted. PACS numbers: 95.30.Cq, 96.60.-j, 25.40.-h There is no record of an attempt to measure the transmutation probability for the fundamental reaction 1H(p, e+,ν)2H. As Bethe and Critchfield [1] predicted a reaction rate of 14(10)9 years no one has been bold enough to test this prediction. Parker and Rolfs [2] wrote “It can be estimated that with a total cross section of 10−47cm2 at Ep(lab) = 1MeV for a proton beam of 1 mA incident on a thick hydrogen target, there would be only one 1H(p, e+,ν)2H reaction in 106 yr.” A similar but numerically discrepant statement appears in Clayton’s classic stellar nucleosynthesis text [3]. As no research team has the patients, resources or longevity to wait out such a prediction it is not surprising that it has never been tested. Such a slow reaction rate was necessary for the standard stellar power model. A much shorter time would cut the lifetime of stars accordingly and a brief reaction time such as seconds would, in that model, cause stars to explode when the reaction conditions were reached.
    [Show full text]
  • Cold Fusion Phenomena May 23-25, 1989 Santa Fe, New Mexico
    WORKSHOP ON COLD FUSION PHENOMENA MAY 23-25, 1989 SANTA FE, NEW MEXICO AGENDA Sponsored by Los Alamos National Laboratory and the U.S. Department of Energy TABLE OF CONTENTS Program Committee V Agenda 1-6 Abstracts of Presentations Sessions A - E WORKSHOP CO-CHAIRMAN Prof. Johann Rafelski Department of Physics Dr. Norman Hackerman University of Arizona The Welch Foundation Tucson, AZ Houston, TX Dr. A. John Appleby Dr. J. Robert Schrieffer Center for Electrochemical Systems Director, Institute for and Hydrogen Research Theoretical Physics Texas A&M University University of California College Station, TX Santa Barbara, CA Dr. Anthony L. Turkevich Enrico Fermi Institute TECHNICAL PROGRAM COORDINATOR University of Chicago Chicago, IL Dr. Reed J. Jensen Los Alamos National Laboratory PROGRAM SUPPORT COORDINATOR Mr. David C. Phillips Los Alamos National Laboratory WORKSHOP PROGRAM COMMITTEE Prof. Allen Bard Department of Chemistry University of Texas Austin, TX Dr. Hans Frauenfelder Department of Physics University of Illinois at Urbana-Champaign Urbana, IL Dr. Steven E. Jones Department of Chemistry Brigham Young University Provo, UT Prof. Arthur K. Kerman Director, Laboratory for Nuclear Science MIT Cambridge, MA Prof. Steve Koonin Institute for Theoretical Physics University of California Santa Barbara, CA AGENDA WORKSHOP ON COLD FUSION PHENOMENA May 22-25, 1989 SWEENEY CENTER, SANTA FE, NM MONDAY, MAY 22 Workshop participants arrive in Santa Fe 4:00 - 8:00 Registration and badge issue at EldoradoHotel -Hospitality room available at EldoradoHotel TUESDAY, MAY 23 7:30 - 8:00 Arrival at Sweeney Center 8:00 - 8:30 Late Registration 8:30 - 9:00 Preliminary Remarks Reed J.
    [Show full text]
  • Stellar Evolution
    AccessScience from McGraw-Hill Education Page 1 of 19 www.accessscience.com Stellar evolution Contributed by: James B. Kaler Publication year: 2014 The large-scale, systematic, and irreversible changes over time of the structure and composition of a star. Types of stars Dozens of different types of stars populate the Milky Way Galaxy. The most common are main-sequence dwarfs like the Sun that fuse hydrogen into helium within their cores (the core of the Sun occupies about half its mass). Dwarfs run the full gamut of stellar masses, from perhaps as much as 200 solar masses (200 M,⊙) down to the minimum of 0.075 solar mass (beneath which the full proton-proton chain does not operate). They occupy the spectral sequence from class O (maximum effective temperature nearly 50,000 K or 90,000◦F, maximum luminosity 5 × 10,6 solar), through classes B, A, F, G, K, and M, to the new class L (2400 K or 3860◦F and under, typical luminosity below 10,−4 solar). Within the main sequence, they break into two broad groups, those under 1.3 solar masses (class F5), whose luminosities derive from the proton-proton chain, and higher-mass stars that are supported principally by the carbon cycle. Below the end of the main sequence (masses less than 0.075 M,⊙) lie the brown dwarfs that occupy half of class L and all of class T (the latter under 1400 K or 2060◦F). These shine both from gravitational energy and from fusion of their natural deuterium. Their low-mass limit is unknown.
    [Show full text]
  • Primordial Nucleosynthesis in the Precision Cosmology Era the Annual Review of Nuclear and Particle Science Gary Steigman (2007)
    Primordial Nucleosynthesis in the Precision Cosmology Era The Annual Review of Nuclear and Particle Science Gary Steigman (2007) Galactic Archeology Seminar Manuel Kramer Universit¨atHeidelberg December 1, 2017 Contents 1 Introduction 2 Fusion of the first nuclides 3 Observations of the relic nuclides 4 Theory vs data 5 Summary Source: CERN Introduction Fusion of the first nuclides Observations of the relic nuclides Theory vs data Summary Fusion of the first nuclides Initial neutron to proton ratio Neutron & Proton equilibrium Once stable hadrons can form from the quark gluon plasma in the very early universe, neutrons and protons are in thermal equilibrium by the weak interactions: − p + e $ n + νe (1) + n + e $ p +ν ¯e Mass of protons is slightly lower than that of the neutrons ni =pi = 1=7 (2) Introduction Fusion of the first nuclides Observations of the relic nuclides Theory vs data Summary Deuterium evolution Deuterium is formed by fusion of a proton and a neutron n + p $ d + γ (3) Significant amounts can only built up when kT . 80 keV −10 The higher the baryon density η10 = 10 (nB=nγ), the higher the interaction rate Introduction Fusion of the first nuclides Observations of the relic nuclides Theory vs data Summary Helium-4 evolution Nucelar fusion processes The starting point for all subsequent fusions is Deuterium Deuterium fusion is a slow reaction Deuterium is immediately converted to 3He and tritium no stable mass-5 nuclides ! bottleneck at 4He Source: https://en.wikipedia.org/ wiki/Big Bang nucleosynthesis Introduction Fusion of
    [Show full text]
  • Modern Physics, the Nature of the Interaction Between Particles Is Carried a Step Further
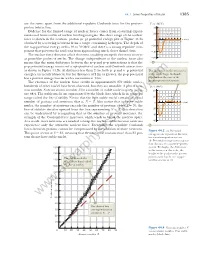
    44.1 Some Properties of Nuclei 1385 are the same, apart from the additional repulsive Coulomb force for the proton– U(r ) (MeV) proton interaction. 40 Evidence for the limited range of nuclear forces comes from scattering experi- n–p system ments and from studies of nuclear binding energies. The short range of the nuclear 20 force is shown in the neutron–proton (n–p) potential energy plot of Figure 44.3a 0 r (fm) obtained by scattering neutrons from a target containing hydrogen. The depth of 1 567432 8 the n–p potential energy well is 40 to 50 MeV, and there is a strong repulsive com- Ϫ20 ponent that prevents the nucleons from approaching much closer than 0.4 fm. Ϫ40 The nuclear force does not affect electrons, enabling energetic electrons to serve as point-like probes of nuclei. The charge independence of the nuclear force also Ϫ60 means that the main difference between the n–p and p–p interactions is that the a p–p potential energy consists of a superposition of nuclear and Coulomb interactions as shown in Figure 44.3b. At distances less than 2 fm, both p–p and n–p potential The difference in the two curves energies are nearly identical, but for distances of 2 fm or greater, the p–p potential is due to the large Coulomb has a positive energy barrier with a maximum at 4 fm. repulsion in the case of the proton–proton interaction. The existence of the nuclear force results in approximately 270 stable nuclei; hundreds of other nuclei have been observed, but they are unstable.
    [Show full text]
  • Astronomy General Information
    ASTRONOMY GENERAL INFORMATION HERTZSPRUNG-RUSSELL (H-R) DIAGRAMS -A scatter graph of stars showing the relationship between the stars’ absolute magnitude or luminosities versus their spectral types or classifications and effective temperatures. -Can be used to measure distance to a star cluster by comparing apparent magnitude of stars with abs. magnitudes of stars with known distances (AKA model stars). Observed group plotted and then overlapped via shift in vertical direction. Difference in magnitude bridge equals distance modulus. Known as Spectroscopic Parallax. SPECTRA HARVARD SPECTRAL CLASSIFICATION (1-D) -Groups stars by surface atmospheric temp. Used in H-R diag. vs. Luminosity/Abs. Mag. Class* Color Descr. Actual Color Mass (M☉) Radius(R☉) Lumin.(L☉) O Blue Blue B Blue-white Deep B-W 2.1-16 1.8-6.6 25-30,000 A White Blue-white 1.4-2.1 1.4-1.8 5-25 F Yellow-white White 1.04-1.4 1.15-1.4 1.5-5 G Yellow Yellowish-W 0.8-1.04 0.96-1.15 0.6-1.5 K Orange Pale Y-O 0.45-0.8 0.7-0.96 0.08-0.6 M Red Lt. Orange-Red 0.08-0.45 *Very weak stars of classes L, T, and Y are not included. -Classes are further divided by Arabic numerals (0-9), and then even further by half subtypes. The lower the number, the hotter (e.g. A0 is hotter than an A7 star) YERKES/MK SPECTRAL CLASSIFICATION (2-D!) -Groups stars based on both temperature and luminosity based on spectral lines.
    [Show full text]
  • Maximizing Specific Energy by Breeding Deuterium
    Maximizing specific energy by breeding deuterium Justin Ball Ecole Polytechnique F´ed´eralede Lausanne (EPFL), Swiss Plasma Center (SPC), CH-1015 Lausanne, Switzerland E-mail: [email protected] Abstract. Specific energy (i.e. energy per unit mass) is one of the most fundamental and consequential properties of a fuel source. In this work, a systematic study of measured fusion cross-sections is performed to determine which reactions are potentially feasible and identify the fuel cycle that maximizes specific energy. This reveals that, by using normal hydrogen to breed deuterium via neutron capture, the conventional catalyzed D-D fusion fuel cycle can attain a specific energy greater than anything else. Simply surrounding a catalyzed D-D reactor with water enables deuterium fuel, the dominant stockpile of energy on Earth, to produce as much as 65% more energy. Lastly, the impact on space propulsion is considered, revealing that an effective exhaust velocity exceeding that of deuterium-helium-3 is theoretically possible. 1. Introduction The aim of this work is to investigate the basic question \What fuel source can provide the most energy with the least mass?" For this question, we will look into the near future and assume that the current incremental and steady development of technology will continue. However, we will not postulate any breakthroughs or new physical processes because they cannot be predicted with any certainty. It is already well-known that the answer to our question must involve fusion fuels [1,2], but nothing more precise has been rigorously establishedz. A more precise answer may be useful in the future arXiv:1908.00834v1 [physics.pop-ph] 2 Aug 2019 when the technology required to implement it becomes available.
    [Show full text]
  • Stellar Nucleosynthesis
    Stellar nucleosynthesis Stellar nucleosynthesis is the creation (nucleosynthesis) of chemical elements by nuclear fusion reactions within stars. Stellar nucleosynthesis has occurred since the original creation of hydrogen, helium and lithium during the Big Bang. As a predictive theory, it yields accurate estimates of the observed abundances of the elements. It explains why the observed abundances of elements change over time and why some elements and their isotopes are much more abundant than others. The theory was initially proposed by Fred Hoyle in 1946,[1] who later refined it in 1954.[2] Further advances were made, especially to nucleosynthesis by neutron capture of the elements heavier than iron, by Margaret Burbidge, Geoffrey Burbidge, William Alfred Fowler and Hoyle in their famous 1957 B2FH paper,[3] which became one of the most heavily cited papers in astrophysics history. Stars evolve because of changes in their composition (the abundance of their constituent elements) over their lifespans, first by burning hydrogen (main sequence star), then helium (red giant star), and progressively burning higher elements. However, this does not by itself significantly alter the abundances of elements in the universe as the elements are contained within the star. Later in its life, a low-mass star will slowly eject its atmosphere via stellar wind, forming a planetary nebula, while a higher–mass star will eject mass via a sudden catastrophic event called a supernova. The term supernova nucleosynthesis is used to describe the creation of elements during the explosion of a massive star or white dwarf. The advanced sequence of burning fuels is driven by gravitational collapse and its associated heating, resulting in the subsequent burning of carbon, oxygen and silicon.
    [Show full text]
  • F .~ I DISCLAIMER
    ---,~ ES·F·'H125.1y U.S. DEPARTMENT OF ENERGY (10-86) '" . I CORRESPONDENCE CONTROL FORM OFFICE OF THE EXECUTIVE SECRETARIAT ACTIVITY (. 1) 0 DO NOT DETACH FROM ORIGINAL CORRESPONDENCE SOURCE.CODE f'N PUB."]( r1Hll... .SPEC INT: CONTROL Nor- ~~ 89 .... ,) 1• ~~ OB O .\TE CORR: ~tH,..,..1 ....,..1 ..,...l ""'O ....,.,,. "''""l8,..,..,9 / :<r DATE CNTRL: O<~J/ l '·l.·· bS' DATE DUE: -------- -------- .R: .:_ MEMO: TWX: TO: SECY: X DEP SEC: UN SEC: OTHER: ----- I (J SUBJ: 1'1 .;J...[A I U~~· .[( N FOR USE BY ACTION OFFICE ONLY ENCL OSES "SHOR f BUfriNAI~Y OF ACTION REFERRED TO DATE RETURN TO DUE RE.:>E ·· F Cll 0 :: U f ON·-I'tDUC :::n DATE CH .·N .. ~REf.~CTIO -~ROLESSEb ~-oR 2 L "'GE·- SC l .:. p WER t •• II 3 ACTION T<(IJ~ TYPEACTION: For vour' infor'M<ltion SIG OF: --~------------- ---- CONCURRENCE: INFORMATION ~ ; DS US t1A/1. 22 DO/I~ 1 FILECODE. MKIM-ESJS 012080 CONTROL ANALYST: TRI-)Vlb HULSEY. I ~j07 ·,; ALL DOCUMENTS FOR THE OFFICE OF THE SECRETARY MUST BE FORWARDED TO THE OFFICE OF THE EXECUTIVE SECRETARIAT FOR FINAL PROCESSING f .~ I DISCLAIMER Portions of this document may be illegible in electronic image products. Images are produced from the best available original document. ' t PURDUE UNIVERSITY DEPARTMENT OF PHYSICS August 10, 1989 Dr. John R . Huizenga Co-Chairman, Cold Fusion Panel U.S. Department of Energy 1000 Independence A venue, SW Washington, D.C. 20585 Dear Dr. Huizenga: As you requested in your letter of July 20, 1989, I am sending you a short summary of my past and present research on nuclear fusion.
    [Show full text]
  • Status and Perspectives of 2, + and 2+ Decays
    Review Status and Perspectives of 2e, eb+ and 2b+ Decays Pierluigi Belli 1,2,*,† , Rita Bernabei 1,2,*,† and Vincenzo Caracciolo 1,2,3,*,† 1 Istituto Nazionale di Fisica Nucleare (INFN), sezione di Roma “Tor Vergata”, I-00133 Rome, Italy 2 Dipartimento di Fisica, Università di Roma “Tor Vergata”, I-00133 Rome, Italy 3 INFN, Laboratori Nazionali del Gran Sasso, I-67100 Assergi, Italy * Correspondence: [email protected] (P.B.); [email protected] (R.B.); [email protected] (V.C.) † These authors contributed equally to this work. Abstract: This paper reviews the main experimental techniques and the most significant results in the searches for the 2e, eb+ and 2b+ decay modes. Efforts related to the study of these decay modes are important, since they can potentially offer complementary information with respect to the cases of 2b− decays, which allow a better constraint of models for the nuclear structure calculations. Some positive results that have been claimed will be mentioned, and some new perspectives will be addressed shortly. Keywords: positive double beta decay; double electron capture; resonant effect; rare events; neutrino 1. Introduction The double beta decay (DBD) is a powerful tool for studying the nuclear instability, the electroweak interaction, the nature of the neutrinos, and physics beyond the Standard Model (SM) of Particle Physics. The theoretical interpretations of the double beta decay Citation: Belli, P.; Bernabei, R.; with the emission of two neutrinos is well described in the SM; the process is characterized Caracciolo, V. Status and Perspectives by a nuclear transition changing the atomic number Z of two units while leaving the atomic of 2e, eb+ and 2b+ Decays.
    [Show full text]
  • Production and Applications of Neutrons Using Particle Accelerators
    INL/EXT-09-17312 Production and Applications of Neutrons Using Particle Accelerators David L. Chichester November 2009 The INL is a U.S. Department of Energy National Laboratory operated by Battelle Energy Alliance INL/EXT-09-17312 Production and Applications of Neutrons Using Particle Accelerators David L. Chichester November 2009 Idaho National Laboratory Idaho Falls, Idaho 83415 http://www.inl.gov Prepared for the U.S. Department of Energy National Nuclear Security Administration Under DOE Idaho Operations Office Contract DE-AC07-05ID14517 CHAPTER X PRODUCTION AND APPLICATIONS OF NEUTRONS USING PARTICLE ACCELERATORS David L. Chichester Idaho National Laboratory 2525 North Fremont Avenue, Idaho Falls, Idaho, United States of America Advances in neutron science have gone hand in hand with the development and of particle accelerators from the beginning of both fields of study. Early accelerator systems were developed simply to produce neutrons, allowing scientists to study their properties and how neutrons interact in matter, but people quickly realized that more tangible uses existed too. Today the diversity of applications for industrial accelerator-based neutron sources is high and so to is the actual number of instruments in daily use is high, and they serve important roles in the fields where they're used. This chapter presents a technical introduction to the different ways particle accelerators are used to produce neutrons, an historical overview of the early development of neutron-producing particle accelerators, a description of some current industrial accelerator systems, narratives of the fields where neutron-producing particle accelerators are used today, and comments on future trends in the industrial uses of neutron producing particle accelerators.
    [Show full text]