DOCSLIB.ORG

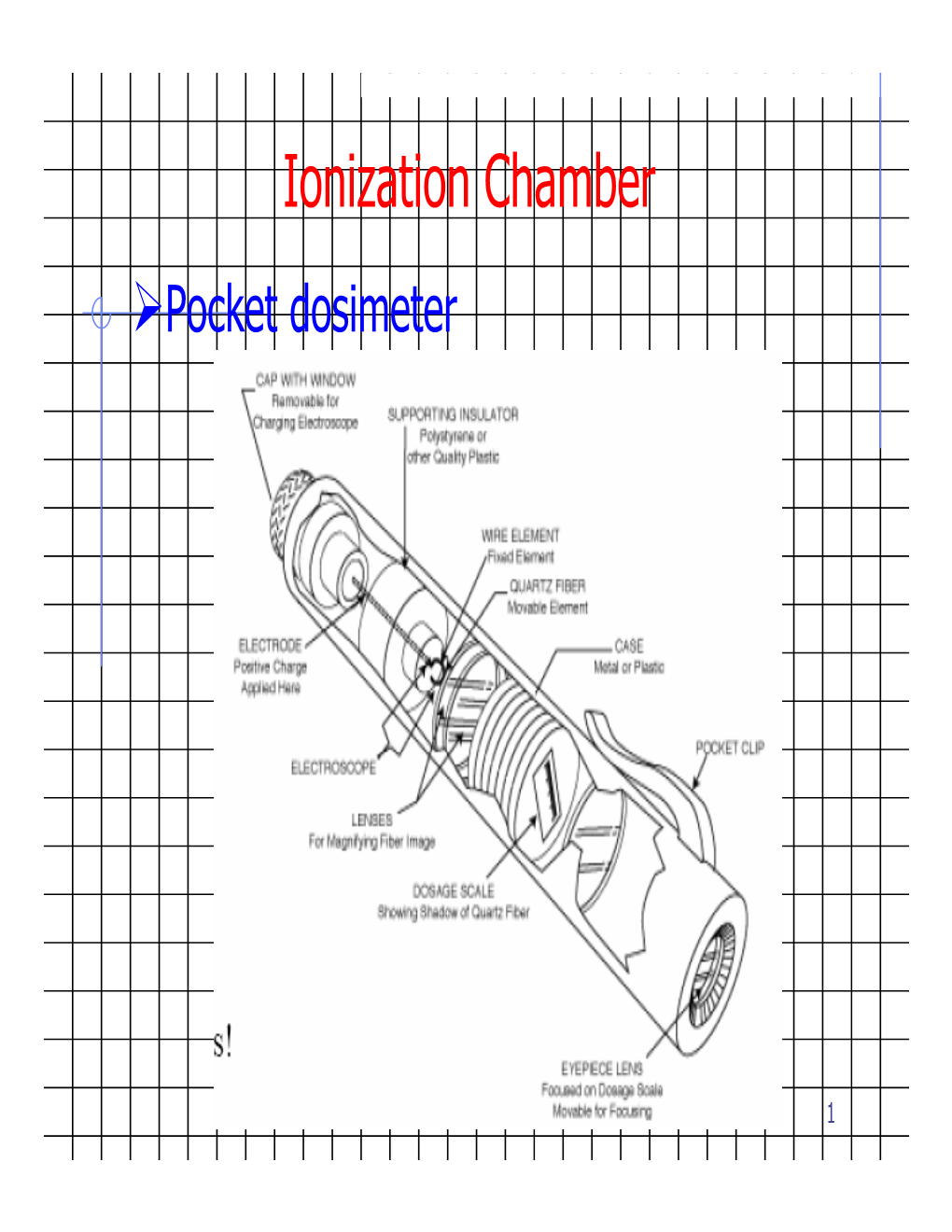
Ionization Chamber ¾Pocket Dosimeter

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ionization Chamber ¾Pocket Dosimeter Ionization Chamber ¾Pocket dosimeter 1 Ionization Chamber ¾Pocket dosimeter 2 Radiation Quantities and Units ¾Radiation measurements require specification of the radiation field at various points At the source – Activity, mA, kVp In flight – Exposure, fluence (dN/dA), energy fluence (dE/dA) At the first interaction point – kerma Kinetic Energy Released in Matter In matter – Absorbed dose, equivalent dose, effective dose Radiation dosimetry is concerned with a quantitative determination of the energy deposited a medium by ionizing radiation 3 Radiation Quantities and Units ¾Pictorially Energy Source Deposition Transport First Interaction 4 Radiation Units ¾Activity 1 Bq (bequerel) == 1 disintegration / s A common unit is MBq = 106 Bq 10 1 Ci (curie) == 3.7x10 disintegrations /s An earlier unit of activity and used in EPP A typical HDR brachytherapy source is 10-20 Ci A typical radioactive source is the lab is ~ 10μCi 40K in your body is 0.1 μCi = 3700 Bq 5 Radiation Units ¾Exposure Defined for x-ray and gamma rays < 3 MeV Measures the amount of ionization (charge Q) in a volume of air at STP with mass m X == Q/m Assumes that the small test volume is embedded in a sufficiently large volume of irradiation that the number of secondary electrons entering the volume equals the number that leave (CPE) Units are C/kg or R (roentgen) 1 R (roentgen) == 2.58 x 10-4 C/kg Somewhat historical unit (R) now but sometimes still found on radiation monitoring instruments X-ray machine might be given as 5mR/mAs at 70 kVp at 100 cm 6 Radiation Units ¾Absorbed dose Energy deposited by ionizing radiation in a volume element of material divided by the mass of the volume D=E/m Related to biological effects in matter Units are grays (Gy) or rads (R) 1 Gy = 1 J / kg = 6.24 x 1012 MeV/kg 1 Gy = 100 rad 1 Gy is a relatively large dose Radiotherapy doses ~ 50 Gy Diagnostic radiology doses 1-30 mGy Typical background radiation ~ 6 mGy 7 Radiation Units ¾Equivalent dose Not all types of radiation cause the same biological damage per unit dose Dense ionization (high LET) along a track causes more biological damage than less dense (low LET) HT=D x wR 8 Radiation Units ¾Effective dose Not all tissues are equally sensitive to ionizing radiation E = ∑ HT ⋅ wT T Used to compare the stochastic risk from an exposure to a specific organ(s) in terms of the equivalent risk from an exposure of the whole body The stochastic risks are carcinogenesis and hereditary effects Not intended for acute effects In practice, most exposures are whole body 9 Radiation Units ¾Tissue weighting factors Sums to 1 Tissue or Organ Tissue weighing factor - wT Gonads 0.20 Bone marrow – red 0.12 Colon 0.12 Lung 0.12 Stomach 0.12 Bladder 0.05 Breast 0.05 Liver 0.05 Oesophagus 0.05 Thyroid 0.05 Skin 0.01 Bone surface 0.01 Remainder 0.05 10 Radiation Units ¾Units of equivalent dose and effective dose are sieverts (Sv) 1 Sv = 100 rem (roentgen equivalent in man) 3.6 (6.2) mSv / year = typical equivalent dose in 1980’s (2006) 15 mSv/ year = Fermilab maximum allowed dose 20 mSv/year = CERN maximum allowed dose 50 mSv/year = US limit 3-4 Sv whole body = 50% chance of death (LD 50/30) 11 Background Radiation ¾Average equivalent dose (1980’s) 12 Background Radiation ¾Average equivalent dose (2006) 13 Background Radiation ¾1980’s versus 2006 14 Radiation in Japan ¾20 mSv / yr = 2.3 μSv/hr ¾3/28 update Reactor 2 @ 1 Sv / hr !!! 15 Fission Yield ¾Some of the more harmful fission products are 90Sr (29y), 106Ru (1y), 131I (8d), 132Te (3d), 133Xe (5d), and 137Cs (30y) 16 Natural Radioactivity 17 Natural Radioactivity ¾Terrestrial Present during the formation of the solar system Uranium, actinium, thorium, neptunium series 40 K ¾Cosmogenic Radionuclides produced in collisions between energetic cosmic rays and stable particles in the atmosphere (14C, 3H, 7Be) ¾Human produced Nuclear medicine, fission reactors, nuclear testing ¾Cosmic rays ~270 μSv / year (a bit more in Tucson) 18 Natural Radioactivity ¾Radon 19 Radon ¾222Rn (radon) is produced in the 238U decay series 222 218 Rn → Po + α (t1/2=3.8 days) 218 214 Po → Pb + α (t1/2=3.1 minutes) ¾Radon is a gas that can easily travel from the soil to indoors Air pressure differences Cracks/openings in a building ¾218Po can be absorbed into the lungs (via dust, etc.) The decay alpha particles are heavily ionizing The ionization in bronchial epithelial cells is believed to initiate carcinogenesis 20 Radiation Units ¾Kerma Kinetic energy released per unit mass Defined for indirectly ionizing energy (photons and neutrons) Mean energy transferred to ionizing particles in the medium without concern as to what happens after the transfer K=Etr/m Units are grays (Gy) 1 Gy = 1 J / kg 21 Radiation Units ¾The energy transferred to electrons by photons (kerma) can be expended in two ways Ionization losses Radiation losses (bremsstrahlung and electron-positron annihilation) Thus we can write K = Kcol + Krad Kcol = K()1− g g is the fraction of energy transferred to electrons that is lost through radiative processes 22 Photon Attenuation Coefficients Review −μx I = I0e μ is the linear attenuation coefficient μ μ = is the mass attenuation coefficient m ρ μen is the energy absorption coefficient μtr is the energy transfer coefficient μen = μtr ()1− g where g is the fraction of energy that is lost in radiative processes 23 Compton Scattering tr sc σ C = σ C +σ C T hv − hv′ σ tr = σ = σ C C hν C hν hv′ σ sc = σ C C hν similarly for the mass energy transfer attenuation coefficient μ tr T μ T N σ C = C = Av C ρ hν ρ hν A 24 Kcol and D as a function of depth 25 Relations ¾Kerma and energy fluence For a monoenergetic photon beam of energy E ⎛ μtr ⎞ K = Ψ⎜ ⎟ ⎝ ρ ⎠E 2 The energy fluence Ψ units are J/m 26 Relations ¾Exposure and kerma ⎛ e ⎞ X = K ⎜ ⎟ col()air ⎜ ⎟ ⎝Wair ⎠ W 33.97eV 1.602×10−19 J / eV air = ⋅ e ion pair 1.602×10−19 C / ionpair = 33.97J / C Wair includes the electron’s binding energy, average kinetic energy of ejected electrons, energy lost in excitation of atoms, … On average, 2.2 atoms are excited for each atom ionized 27 Relations ¾Absorbed dose and kerma D = Kcol = K(1− g) g is the radiative fraction g depends on the electron kinetic energy as well as the material under consideration The above relation assumes CPE ¾In theory, one can thus use exposure X to determine the absorbed dose Assumes CPE Limited to photon energies below 3 MeV 28 Kcol and D as a function of depth β=D/Kcol 29 Kcol and D as a function of depth ¾In the TCPE region, β = D/Kcol > 1 Photon beam is being attenuated Electrons are produced (generally) in the forward direction 30 Bragg-Gray Cavity Theory ¾The main question is, how does one determine or measure the absorbed dose delivered to the patient (to within a few percent) The answer is to use ionization in an air ion chamber placed in a medium The ionization can then be related to energy absorbed in the surrounding medium 31 Bragg-Gray Cavity Theory ¾Assumes Cavity is small (< Relectrons) so that the fluence of charged particles is not perturbed (CPE) Absorbed dose in the cavity comes solely by charged particles crossing it (i.e. no electrons are produced in the cavity or stop in the cavity) ⎛ S ⎞ ⎛ S ⎞ Dmed = Dcav ⎜ ⎟ /⎜ ⎟ ⎝ ρ ⎠med ⎝ ρ ⎠cav S is the average unrestricted mass collision stopping power Q W ⎛ IP ⎞⎛ eV ⎞ ⎛ eV ⎞ eV Dcav = ⋅ = ⎜ ⎟⎜ ⎟ ; ⎜ ⎟ = 33.97 for air m e ⎝ kg ⎠⎝ IP ⎠ ⎝ IP ⎠ IP 32 Bragg-Gray Cavity Theory ¾Spencer-Attix modification Accounts for delta rays that may escape the cavity volume In this case, one uses the restricted stopping power (energy loss) ⎛ L ⎞ ⎛ L ⎞ Dmed = Dcav ⎜ ⎟ /⎜ ⎟ ⎝ ρ ⎠med ⎝ ρ ⎠cav L is the average restricted mass collision stopping power 33 Calibration of MV Beams ¾Protocols exist to calibrate the absorbed dose from high energy photon and electron beams End result is a measurement of dose to water per MU (monitor unit = 0.01 Gy) For a reference depth, field size, and source to surface distance (SSD) ¾TG-21 Outdated but conceptually nice Based on cavity-gas calibration factor Ngas ¾TG-51 New standard Based on absorbed dose to water calibration 60 factor ND,w for Co 34 Ionization Chamber ¾Ionization chambers are a fundamental type of dosimeter in radiation physics ¾Measurement of the current or charge or reduction in charge gives the exposure or absorbed dose Free-air ionization chamber Thimble chamber Plane parallel chamber Pocket dosimeter 35 Ionization Chamber ¾Current mode Current gives average rate of ion formation of many particles ¾Pulse mode Voltage gives measure of individual charged particle ion formation 36 Ionization Chamber ¾Free-air chamber 37 Ionization Chamber ¾Used as a primary standard in standards laboratories ¾Used to measure X Q −μx′ X ()R = −4 e AP Lρ ⋅2.58×10 ¾Guard wires and guard electrodes produce uniform electric field ¾E ~ 100-200V/cm between plates ¾Assumes CPE ¾Limited to E<3 MeV (if pressurized) because of electron range 38 Ionization Chamber ¾Free-air chambers are not so practical however Instead one uses an ion chamber with a solid, air equivalent wall 39 Ion Chambers EXRADIN A12 Farmer EXRADIN A3 Spherical Chamber EXRADIN 11 Parallel Plate Chamber EXRADIN A17 Farmer EXRADIN mini thimble EXRADIN A12 thimble 40 Ionization Chamber ¾Vendors Capintec Inc.
Load more

Recommended publications
  • Low Dose Radiation Therapy for Severe COVID-19 Pneumonia: a Randomized Double- Blind Study --Manuscript Draft
    International Journal of Radiation Oncology • Biology • Physics Low dose radiation therapy for severe COVID-19 pneumonia: a randomized double- blind study --Manuscript Draft-- Manuscript Number: ROB-D-21-00260R1 Article Type: Full Length Article Section/Category: Clinical Investigation - Other Corresponding Author: Alexandros Papachristofilou University Hospital Basel: Universitatsspital Basel Basel, SWITZERLAND First Author: Alexandros Papachristofilou, MD Order of Authors: Alexandros Papachristofilou, MD Tobias Finazzi, MD Andrea Blum, MD Tatjana Zehnder, MD Núria Zellweger Jens Lustenberger, MD Tristan Bauer, MD Christian Dott Yasar Avcu, M.Sc. Goetz Kohler, PhD Frank Zimmermann, MD Hans Pargger, MD Martin Siegemund, MD Abstract: Purpose The morbidity and mortality of patients requiring mechanical ventilation for coronavirus disease 2019 (COVID-19) pneumonia is considerable. We studied the use of whole- lung low dose radiation therapy (LDRT) in this patient cohort. Methods and Materials Patients admitted to the intensive care unit (ICU) and requiring mechanical ventilation for COVID-19 pneumonia were included in this randomized double-blind study. Patients were randomized to 1 Gy whole-lung LDRT or sham irradiation (sham-RT). Treatment group allocation was concealed from patients and ICU clinicians, who treated patients according to the current standard of care. Patients were followed for the primary endpoint of ventilator-free days (VFDs) at day 15 post-intervention. Secondary endpoints included overall survival, as well as changes in oxygenation and inflammatory markers. Results Twenty-two patients were randomized to either whole-lung LDRT or sham-RT between November and December 2020. Patients were generally elderly and comorbid, with a median age of 75 years in both arms. No difference in 15-day VFDs was observed between groups (p = 1.00), with a median of 0 days (range, 0-9) in the LDRT arm, and 0 days (range, 0-13) in the sham-RT arm.
    [Show full text]
  • 12VAC5-481-10. Definitions
    Virginia Administrative Code Title 12. Health Agency 5. Department of Health Chapter 481. Virginia Radiation Protection Regulations 12VAC5-481-10. Definitions. Part I. General Provisions The following words and terms as used in this chapter shall have the following meanings unless the context clearly indicates otherwise: "A1" means the maximum activity of special form radioactive material permitted in a Type A package. This value is listed in Table 1 of 12VAC5-481-3770 F. "A2" means the maximum activity of radioactive material, other than special form radioactive material, LSA, and SCO material, permitted in a Type A package. This value is listed in Table 1 of 12VAC5-481-3770 F. "Absorbed dose" means the energy imparted by ionizing radiation per unit mass of irradiated material. The units of absorbed dose are the gray (Gy) and the rad. "Absorbed dose rate" means absorbed dose per unit time, for machines with timers, or dose monitor unit per unit time for linear accelerators. "Accelerator" means any machine capable of accelerating electrons, protons, deuterons, or other charged particles in a vacuum and of discharging the resultant particulate or other radiation into a medium at energies usually in excess of one MeV. For purposes of this definition, "particle accelerator" is an equivalent term. "Accelerator-produced material" means any material made radioactive by a particle accelerator. "Access control" means a system for allowing only approved individuals to have unescorted access to the security zone and for ensuring that all other individuals are subject to escorted access. "Accessible surface" means the external surface of the enclosure or housing of the radiation producing machine as provided by the manufacturer.
    [Show full text]
  • Manual for ACRO Accreditation March 2016
    American College of Radiation Oncology Manual for ACRO Accreditation March 2016 Powered by Patients First Our Focus is Radiation Oncology Safety! ACKNOWLEDGMENTS ACRO expresses its appreciation for the significant contribution and leadership of Jaroslaw Hepel, MD, FACRO, Chair of the ACRO Standards Committee, and ACRO Accreditation Medical Director, for his un- tiring efforts to bring this version of the Manual for ACRO Accreditation to publication. Thanks also go to Arve Gillette, MD, FACRO, ACRO Chancellor and a former President, and ACRO Ac- creditation Medical Director during 2011, who initiated most of the new procedures incorporated in the accreditation program when it was reintroduced after a board imposed administrative review for most of 2010. Appreciation also is expressed to Ralph Dobelbower, MD, FACRO, the founding medical director of ACRO Accreditation; Gregg Cotter, MD, FACRO, medical director after Dr. Dobelbower; and Ishmael Parsai, PhD, FACRO, physics chairman for many years; for their collective leadership in building the accreditation program from its inception in 1995. In addition, appreciation is expressed for ongoing support and commitment to the accreditation process to all the following ACRO members who have contributed, and continue to contribute, to the success of ACRO Accreditation: ACRO Executive Committee | Drs. James Welsh (President), Eduardo Fernandez (Vice President), William Rate (Secretary-Treasurer), and Arno Mundt (Chairman) ACRO Chancellors | Drs. Joanne Dragun, Gregg Franklin, Shane Hopkins, Sheila Rege, Charles Thomas, II, Harvey Wolkov, Catheryn Yashar, and Luther Brady (ex officio) ACRO Accreditation Disease Site Team Leaders | Dr. Jaroslaw Hepel (Breast Cancer); Drs. William Regine & Navesh Sharma (Gastrointestinal Cancer); Dr. Peter Orio III (Genitourinary Cancer); Dr.
    [Show full text]
  • REGULATIONS and STATUTES Kansas Radiation Control Program
    REGULATIONS AND STATUTES Kansas Radiation Control Program Unofficial Copy The regulations and statutes provided are for the convenience of the user but are not considered the official regulations. For more information on the official regulations, visit the Kansas Secretary of State website. For more information about official copies of statutes, visit the Kansas Legislature website. April 27, 2021 [email protected] Kansas Administrative Regulations Table of Contents Table of Contents Kansas Annotated Regulations ........................................... 2 Part 1. Definitions ............................................................... 2 Part 2. Radiation Producing Machines ............................. 67 Part 3. Licensing of Sources of Radiation ........................ 75 Part 4. Standards for Protection Against Radiation ........ 190 Part 5. Use of X-Rays in the Healing Arts ...................... 249 Part 6. Use of Sealed Radioactive Sources in the Healing Arts .............................................................................................. 291 Part 7. Special Requirements for Industrial Radiographic Operations ................................................................................... 294 Part 8. Radiation Safety Requirements for Analytical X- Ray Equipment............................................................................ 319 Part 9. Radiation Safety Requirements for Particle Accelerators ................................................................................ 323 Part 10. Notices, Instructions
    [Show full text]
  • Towards Safer Radiotherapy
    Patient Safety Division The Royal College of Radiologists IPEM Towards Safer Radiotherapy British Institute of Radiology Institute of Physics and Engineering in Medicine National Patient Safety Agency Society and College of Radiographers The Royal College of Radiologists Contents Foreword 4 Executive summary 5 Chapter 1 Introduction 7 Chapter 2 Nature and frequency of human errors in radiotherapy 8 Chapter 3 Defining and classifying radiotherapy errors 18 Chapter 4 Prerequisites for safe delivery of radiotherapy 24 Chapter 5 Detection and prevention of radiotherapy errors 35 Chapter 6 Learning from errors 48 Chapter 7 Dealing with consequences of radiotherapy errors 53 Summary of recommendations 58 3 Appendices Appendix 3.1 61 Appendix 4.1 69 Appendix 6.1 70 References 71 Further reading 77 Glossary of terms 78 Abbreviations 82 Membership of Working Party 84 Towards Safer Radiotherapy Foreword In my Annual Report on the State of Public Health in 2006,1 I drew attention to the problem of radiotherapy safety. Overall, radiotherapy in the United Kingdom offers a first-rate service providing high-quality care to the vast majority of patients every year. However, in a number of unfortunate cases over the last few years, overdoses of radiation led to severe harm to patients. It is recognised that these are uncommon events, yet their impact on the patient, staff involved and the wider health service are devastating. Not only does it compromise the delivery of radiotherapy, it calls into question the integrity of hospital systems and their ability to pick up errors and the capability to make sustainable changes. While further investment in radiotherapy is a continuing desirable goal, the patient safety movement has started to establish that changing the culture of an organisation involves steps more sophisticated than just investment and human resources.
    [Show full text]
  • Acceptance Tests and Commissioning Measurements
    Chapter 10: Acceptance Tests and Commissioning Measurements Set of 189 slides based on the chapter authored by J. L. Horton of the IAEA publication: Review of Radiation Oncology Physics: A Handbook for Teachers and Students Objective: To familiarize the student with the series of tasks and measurements required to place a radiation therapy machine into clinical operation. Slide set prepared in 2006 by G.H. Hartmann (Heidelberg, DKFZ) Comments to S. Vatnitsky: [email protected] IAEA International Atomic Energy Agency CHAPTER 10. TABLE OF CONTENTS 10.1 Introduction 10.2 Measurement Equipment 10.3 Acceptance Tests 10.4 Commissioning 10.5 Time Requirements IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 10. 1 10.1 INTRODUCTION In many areas of radiotherapy, particularly in the more readily defined physical and technical aspects of a radiotherapy unit, the term “Quality Assurance”(QA) is frequently used to summarize a variety of actions • to place the unit into clinical operation, and • to maintain its reliable performance. Typically, the entire chain of a QA program for a radiotherapy unit consists of subsequent actions as shown in the following slide. IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 10.1 Slide 1 10.1 INTRODUCTION Subsequent QA actions Purpose • Clinical needs assessment Basis for specification • Initial specification and purchase Specification of data in units of measure, process design of a tender • Acceptance testing Compliance with specifications • Commissioning for clinical use, Establishment of baseline performance (including calibration) values Monitoring the reference performance • Periodic QA tests values • Additional quality control tests after Monitoring possibly changed reference any significant repair, intervention, performance values or adjustment • Planned preventive maintenance Be prepared in case of malfunctions etc.
    [Show full text]
  • Overview and Basis of Design for NCRP Report
    This Report was prepared through a joint effort of NCRP Scientific Committee 46-13 on Design of Facilities for Medical Radiation Overview & Basis of Design for NCRP Therapy and AAPM Task Group 57. Report 151 James A. Deye, Chairman James E. Rodgers, Vice Chair Raymond K. Wu, Vice Chair Structural Shielding Design and Evaluation for Peter J. Biggs Patton H. McGinley Megavoltage x- and Gamma-ray Radiotherapy Facilities Richard C. McCall Liaisons Kenneth R. Kase Marc Edwards Raymond K. Wu, PhD Consultants OhioHealth Hospitals Robert O. Gorson Jeffrey H. Kleck Nisy E. Ipe Columbus, OH Secretariat Marvin Rosenstein Eric E. Kearsley Learn • Calculation methods • W, U, T, IDR, TADR, RW, Rh, • Dose at maze door • Neutron, capture gamma at door • Laminated primary barrier This Report addresses the structural shielding design New Issues since NCRP # 49 and evaluation for medical use of megavoltage x- and gamma-rays for radiotherapy and supersedes related – New types of equipment, material in NCRP Report No. 49, Structural Shielding – Some with energies above 10 MV, Design and Evaluation for Medical Use of X Rays and Gamma Rays of Energies Up to 10 MeV, which was – Many new uses for radiotherapy equipment, issued in September 1976. – Dual energy machines, The descriptive information in NCRP Report No. 49 unique to x-ray therapy installations of less than 500 – Room designs without mazes, kV (Section 6.2) and brachytherapy is not included in – Varied shielding materials including composites, this Report and that information in NCRP Report No. 49 for those categories is still applicable. – More published data on empirical methods.
    [Show full text]
  • Radiation Vault Design and Shielding
    Radiation Vault Design and Shielding Rajat Kudchadker, PhD Associate Professor Department of Radiation Physics NCRP Report No. 151 This report addresses the structural shielding design and evaluation for medical use of megavoltage x- and gamma- rays for radiotherapy and supersedes related material in NCRP Report No. 49, Structural Shielding Design and Evaluation for Medical Use of X Rays and Gamma Rays of Energies Up to 10 MeV, which was issued in September 1976. The descriptive information in NCRP Report No. 49 unique to x-ray therapy installations of less than 500 kV and brachytherapy is not included in this Report and that information in NCRP Report No. 49 for those categories is still applicable. Similarly therapy simulators are not covered in this report and the user is referred to the recent Report 147 for shielding of imaging facilities. NCRP Report No. 151 New Issues since NCRP # 49 • New types of equipment with energies above 10 MV • Many new uses for radiotherapy equipment • Dual energy machines and new treatment techniques • Room designs without mazes • Varied shielding materials including composites • More published data on empirical methods New Modalities New modalities include: • Cyberknife Robotic arm linacs No fixed isocenter All barriers except ceiling are primary Uses only 6 MV • Helical Tomotherapy Radiotherapy CT Uses only 6 MV Uses a beam stopper • Serial Tomotherapy MIMIC device attached to conventional linac Uses table indexer to simulate helical treatment Outdated Special Procedures New modalities include: • Intensity Modulated Radiation Therapy (IMRT) Usually at 6 MV Leakage workload >>primary, scatter workload Could be >50% of the workload on a linac • Stereotactic radiosurgery Use factors are different from 3D CRT High dose, however long setup times • Total Body Irradiation (TBI) Source of scatter is not at the isocenter Primary, leakage workload is greater than prescribed dose NCRP Report No.
    [Show full text]
  • 4732.0110 DEFINITIONS. Subpart 1. Scope. for Purposes of This Chapter, the Terms in This Part Have the Meanings Given Them
    1 REVISOR 4732.0110 4732.0110 DEFINITIONS. Subpart 1. Scope. For purposes of this chapter, the terms in this part have the meanings given them. Subp. 2. Absorbed dose. "Absorbed dose" means the energy imparted by ionizing radiation per unit mass of irradiated material. The special unit of absorbed dose is the rad under the conventional system of measurement and is the gray under the SI system of measurement. Subp. 3. Absorbed dose rate. "Absorbed dose rate" means absorbed dose per unit time for machine with timers, or dose-monitor unit per unit time for linear accelerators. Subp. 4. Accelerator. "Accelerator" means any machine capable of accelerating electrons, protons, deuterons, or other charged particles in a vacuum and of discharging the resultant particulate or other radiation into a medium at energies usually in excess of 1 MeV. For purposes of this definition, linear accelerator, particle accelerator, and cyclotron are equivalent terms. Subp. 5. Added filtration. "Added filtration" means filtration that is in addition to the inherent filtration. Subp. 6. Adult. "Adult" means an individual 18 or more years of age or older. Subp. 7. Air kerma (K). "Air kerma (K)" means the kinetic energy released in air by ionizing radiation. Kerma is determined as the quotient of dE by dM, where dE is the sum of the initial kinetic energies of all the charged ionizing particles liberated by uncharged ionizing particles in air of mass dM. The special name for the unit of kerma is the gray (Gy). The SI unit is joule per kilogram. Subp. 8. Aluminum equivalent. "Aluminum equivalent" means the thickness of type 1100 aluminum alloy affording the same attenuation, under specified conditions, as the material in question.
    [Show full text]
  • Abbreviations and Acronyms
    Review of Radiation Oncology Physics: A Handbook for Teachers and Students ABBREVIATIONS AND ACRONYMS AAPM American Association of Physicists in Medicine ACR American College of Radiology ADCL Accredited Dosimetry Calibration Laboratory ALARA As low as reasonably achievable AP Anterio-posterior A-Si Amorphous silicon BAT B-mode acquisition and targeting BE Binding energy BEV Beam’s eye view B-G Bragg-Gray BGO Bismuth germanate BIPM Bureau International des Poides et Measures (France) BJR British Journal of Radiology BMT Bone marrow transplantation BNCT Boron neutron capture therapy BSF Back-scatter factor BSS Basic Safety Standards CAX Central axis CE Compton effect CEMA Converted energy per unit mass CET Coefficient of equivalent thickness CF Collimator factor CHART Continuous hyperfractionated accelerated radiation therapy CIOMS Council for International Organizations of Medical Sciences CNS Central nervous system CNT Carbon nanotube CPE Charged particle equilibrium CPU Central processing unit CSDA Continuous slowing down approximation CT Computed tomography CT-Sim CT-simulator CTV Clinical target volume DCR Digitally composited radiographs DICOM Digital imaging and communications in medicine DIN Deutches Institut für Normung (Germany) DMF Dose modifying factor DNA Deoxyribonucleic acid DRR Digitally reconstructed radiographs DVH Dose-volume histogram EBF Electron backscatter factor EM Electromagnetic EPID Electronic portal imaging device EPR Electron paramagnetic resonance ESR Electron spin resonance ESTRO European Society for Therapeutic
    [Show full text]
  • Clinical Treatment Planning in External Photon Beam Radiotherapy
    Chapter 7: Clinical Treatment Planning in External Photon Beam Radiotherapy Set of 232 slides based on the chapter authored by W. Parker, H. Patrocinio of the IAEA publication (ISBN 92-0-107304-6): Review of Radiation Oncology Physics: A Handbook for Teachers and Students Objective: To familiarize the student with a variety of modern photon beam radiotherapy techniques to achieve a uniform dose distribution inside the target volume and a dose as low as possible in the healthy tissues surrounding the target. Slide set prepared in 2006 by G.H. Hartmann (Heidelberg, DKFZ) Comments to S. Vatnitsky: [email protected] Version 2012 IAEA International Atomic Energy Agency CHAPTER 7. TABLE OF CONTENTS 7.1 Introduction 7.2 Volume Definition 7.3 Dose Specification 7.4 Patient Data Acquisition and Simulation 7.5 Clinical Considerations for Photon Beams 7.6 Treatment Plan Evaluation 7.7 Treatment Time and Monitor Unit Calculations IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 7.Slide 1 7.1 INTRODUCTION General considerations for photon beams Almost a dogma in external beam radiotherapy: Successful radiotherapy requires a uniform dose distribution within the target (tumor). External photon beam radiotherapy is usually carried out with multiple radiation beams in order to achieve a uniform dose distribution inside the target volume and a dose as low as possible in healthy tissues surrounding the target. IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 7.1 Slide 1 7.1 INTRODUCTION Criteria of a uniform dose distribution within the target Recommendations regarding dose uniformity, prescribing, recording, and reporting photon beam therapy are set forth by the International Commission on Radiation Units and Measurements (ICRU).
    [Show full text]
  • QUALITY CONTROL of MODERN LINEAR ACCELERATOR: DOSE STABILITY LONG and SHORT-TERM Md Tofiz Uddin, National Institute of Cancer Research and Hospital, Dhaka, Bangladesh
    WEPPD061 Proceedings of IPAC2012, New Orleans, Louisiana, USA QUALITY CONTROL OF MODERN LINEAR ACCELERATOR: DOSE STABILITY LONG AND SHORT-TERM Md Tofiz Uddin, National Institute of Cancer Research and Hospital, Dhaka, Bangladesh Abstract reference instrument. The measurements are carried out Quality Control (QC) data of modern linear with relatively long time intervals since they are workful accelerators, collected by National Institute of Cancer and time consuming. Research and Hospital, Dhaka, Bangladesh between the Approximated constancy checks (CC) of output are years 2006 and 2010, were analyzed. Three Linear carried out more often by using by fast and easily Accelerators is included in this work. The goal was to movable equipment. A CC device may not be very stable provide information for the evaluation and elaboration of requiring regular calibrations against the local reference QC of accelerator outputs and to propose a method for instrument [4]. The use of an appropriate QC procedure QC data analysis. Short- and long-term drifts in outputs for output should maximize the detection of both ‘normal’ were quantified by fitting empirical mathematical models and unexpected changes in output levels. QC programs to the QA measurements. Normally, long-term drifts were given by different international or national authorities well (≤1.5%) modeled by either a straight line or a single- have recommended considerable variable time intervals exponential function. A drift of 2% occurred in 18 ± 12 for the output measurements ranging from one week to months. The shortest drift times of only 2–3 months were even one year. Intuitively it is safer to have short output observed for some new accelerators just after the measurement intervals but too redundant measurements commissioning but they stabilized during the first 2–3 waste resources and time that could be used for treatments years.
    [Show full text]