A Drag Coefficient for Application to the WLTP Driving Cycle
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Quantitative Analysis of Drag Reduction Methods for Blunt Shaped Automobiles
applied sciences Review Quantitative Analysis of Drag Reduction Methods for Blunt Shaped Automobiles Ferenc Szodrai Department of Building Services and Building Engineering, Faculty of Engineering, University of Debrecen, 4028 Debrecen, Hungary; [email protected] Received: 30 April 2020; Accepted: 19 June 2020; Published: 23 June 2020 Abstract: In fluid mechanics, drag related problems aim to reduce fuel consumption. This paper is intended to provide guidance for drag reduction applications on cars. The review covers papers from the beginning of 2000 to April 2020 related to drag reduction research for ground vehicles. Research papers were collected from the library of Science Direct, Web of Science, and Multidisciplinary Digital Publishing Institute (MDPI). Achieved drag reductions of each research paper was collected and evaluated. The assessed research papers attained their results by wind tunnel measurements or calculating validated numerical models. The study mainly focuses on hatchback and notchback shaped ground vehicle drag reduction methods, such as active and passive systems. Quantitative analysis was made for the drag reduction methods where relative and absolute drag changes were used for evaluations. Keywords: active flow control; passive flow control; coefficient of drag; ground vehicle; car 1. Introduction In the field of fluid mechanics, drag related problems are fascinating to examine. With a small modification of complex geometry, flow aerodynamics can be changed; thus, less energy will be needed for the propulsion system for a vehicle. Drag related problems were first examined in the aeronautical industry after the automotive industry also realised that it could affect fuel consumption reduction. For ground vehicles, drag related problems are specific due to external effects, such as road inclination and wind. -
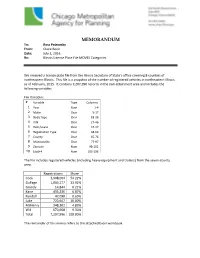
License Plate MOVES Categories Memorandum
MEMORANDUM To: Ross Patronsky From: Claire Bozic Date: July 1, 2016 Re: Illinois License Plate File MOVES Categories We received a license plate file from the Illinois Secretary of State’s office covering 8 counties of northeastern Illinois. This file is a snapshot of the number of registered vehicles in northeastern Illinois as of February, 2015. It contains 7,207,996 records in the non-attainment area and includes the following variables. File Variables # Variable Type Columns 1 Year Num 1-4 2 Make Char 5-17 3 Body Type Char 18-26 4 VIN Char 27-46 5 Rent/Lease Char 47-47 6 Registration Type Char 48-64 7 County Char 65-76 8 Municipality Char 77-97 9 Zipcode Num 98-102 10 (zip)+4 Num 103-106 The file includes registered vehicles (including heavy equipment and trailers) from the seven-county area. Registrations Share Cook 3,908,004 54.22% DuPage 1,003,177 13.92% Grundy 14,844 0.21% Kane 495,236 6.87% Kendall 47,098 0.65% Lake 720,667 10.00% McHenry 348,302 4.83% Will 670,668 9.30% Total 7,207,996 100.00% The remainder of this memo refers to the attached Excel workbook. SAS_Summary Tab The dataset was processed to result in a cross-tabulation of body type by registration type for all records in the file. Added to the table are two calculated fields: MOVES category describing the body type (body_cat) and MOVES category describing the registration type (regi_cat). These fields are filled in by the lookup tables shown on the lookups tabs, discussed in the next section. -

VRG Class SVRA Class
VRG Class SVRA Class SCCA Class Years Make Model Series Displacement Carbs Brakes Comments CPV 3/CP Abarth-Simca 1300 FPV 1/FP AC Ace 1991 AC engine DPV 3/DP AC Ace Bristol 1971 Bristol FPV 1/FP AC Aceca 1991 AC engine DPV 3/DP AC Aceca Bristol 1971 Bristol APV 6/AP AC Cobra 427 BPV 6/BP AC Cobra 289 Alfa Romeo Spiders: HPV 1/HP 1955-1962 Alfa Romeo Giulietta Spider 1290 1x Solex FPV 1/FP 1956-1962 Alfa Romeo Giulietta Spider Veloce 1290 2x Weber FPV 1/FP 1963-1965 Alfa Romeo Giulia Spider 1570 1x Solex EPV 3/EP 1965 Alfa Romeo Giulia Spider Veloce 1570 2x Weber FPV 1/FP Alfa Romeo Duetto Spider Jr 1300 EPV 3/EP 1966-1967 Alfa Romeo Duetto 1570 Twin Weber EPV 3/EP 1968-1971 Alfa Romeo Spider (Veloce, 1750) 1779 2x Weber or Spica FI CPV 3/CP 1972 - on Alfa Romeo Spider (Veloce, 2000) 1962 2x Weber or Spica FI DPH 8/DP 1972 - on Alfa Romeo Spider (Veloce, 2000) 1962 2x Weber or Spica FI Alfa Romeo Coupes: HPV n/a 1954-1962 Alfa Romeo Giulietta Sprint 1290 1x Solex GPV 1/GP 1956-1962 Alfa Romeo Giulietta Sprint Veloce 1290 2x Weber FPv n/a 1963-1964 Alfa Romeo Giulia Sprint 101 1570 1x Solex CSV 1/CS Alfa Romeo GT Jr 1290 BSv 3/BS 1963-1965 Alfa Romeo Giulia Sprint GT 105 1570 2x Weber BSv 3/BS 1965-1968 Alfa Romeo GTV 1570 2x Weber TA2 8/BS 1967-1972 Alfa Romeo GTV 1779 2x Weber or Spica FI TA2 8/BS 1971-1974 Alfa Romeo GTV 1962 2x Weber or Spica FI TA2 8/BS Alfa Romeo GTA 1779 or 1962 CSV 1/CS Alfa Romeo GTA Jr 1290 1970-1971 Alfa Romeo GTAm 1779 or 1962 Spica FI or Lucas FI Alfa Romeo Sedans: CSv n/a 1955-1963 Alfa Romeo Giulietta Berlina -

Numerical and Experimental Investigations on the Aerodynamic Characteristic of Three Typical Passenger Vehicles
Journal of Applied Fluid Mechanics, Vol. 7, No. 4, pp. 659-671, 2014. Available online at www.jafmonline.net, ISSN 1735-3572, EISSN 1735-3645. Numerical and Experimental Investigations on the Aerodynamic Characteristic of Three Typical Passenger Vehicles Y. Wang1, 2†, Y. Xin1, Zh. Gu3, Sh. Wang3, Y. Deng1 and X. Yang4 1Hubei Key Laboratory of Advanced Technology of Automotive Parts, Wuhan University of Technology, Wuhan 430070, China 2State Key Laboratory of Automotive Simulation and Control, Changchun 130025, China 3State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Changsha 430082, China 4Wuhan Ordnance Noncommissioned officers School, Wuhan 430075, China † Corresponding Author Email: [email protected] (Received September 6, 2013; accepted November 11, 2013) ABSTRACT The numerical simulation and wind tunnel experiment were employed to investigate the aerodynamic characteristics of three typical rear shapes: fastback, notchback and squareback. The object was to investigate the sensibility of aerodynamic characteristic to the rear shape, and provide more comprehensive experimental data as a reference to validate the numerical simulation. In the wind tunnel experiments, the aerodynamic six components of the three models with the yaw angles range from -15 and 15 were measured. The realizable k-ε model was employed to compute the aerodynamic drag, lift and surface pressure distribution at a zero yaw angle. In order to improve the calculation efficiency and accuracy, a hybrid Tetrahedron-Hexahedron- Pentahedral-Prism mesh strategy was used to discretize the computational domain. The computational results showed a good agreement with the experimental data and the results revealed that different rear shapes would induce very different aerodynamic characteristic, and it was difficult to determine the best shape. -

2007 ACURA SAMPLE VIN: JH4KB16567C000000 2007 AUDI (Continued) MODEL: KB165 SAMPLE VIN: WAUHF78P37A000000
2007 ACURA SAMPLE VIN: JH4KB16567C000000 2007 AUDI (continued) MODEL: KB165 SAMPLE VIN: WAUHF78P37A000000 MODEL: HF78 BODY TYPE MODEL BASE PRICE BODY TYPE MODEL BASE PRICE ACURA MDX AUDI A4 QUATTRO – 4 x 4 Station Wagon (SUV) YD282 $39,995 4 Door Sedan/6 Speed Transmission − 4 cyl. DF78, DF98 $30,340 Station Wagon (SUV) with Technology Package YD283 43,495 4 Door Sedan/6 Speed Trans. − 4 cyl. − S-Line EF78, EF98 33,740 Station Wagon (SUV) with Technology Package 4 Door Sedan/Automatic Transmission − 4 cyl. DF78, DF98 31,540 and Entertainment System YD284 45,595 4 Door Sedan/Automatic Trans. − 4 cyl. − S-Line EF78, EF98 34,940 Station Wagon (SUV) with Sport Package YD285 45,695 4 Door Sedan/6 Speed Transmission – 6 cyl. DH78, DH98 36,440 Station Wagon (SUV) with Sport Package 4 Door Sedan/6 Speed Trans. – 6 cyl. – S-Line EH78, EH98 39,190 and Entertainment System YD288 47,795 4 Door Sedan/Automatic Trans. − 6 cyl. DH78, DH98 37,640 4 Door Sedan/Automatic Trans. − 6 cyl. − S-Line EH78, EH98 40,390 ACURA RDX Station Wagon (SUV) TB182 32,995 AUDI A6 Station Wagon (SUV) – Technocharged TB185 36,495 4 Door Sedan – 6 cyl. AH74, AH94 41,950 4 Door Sedan − 6 cyl. − S-Line model BH74, BH94 45,500 ACURA RL 4 Door Sedan KB165 45,780 AUDI A6 AVANT QUATTRO − 4 x 4 4 Door Sedan with Technology Package KB166 49,400 Station Wagon − 6 cyl. H74, KH94 48,000 4 Door Sedan − Hawaii KB163 48,665 Station Wagon − 6 cyl. -

Dmv 349 Crash Report Data Element Dictionary
DMV 349 CRASH REPORT DATA ELEMENT DICTIONARY for North Carolina for North Published January 29, 2015 By: North Carolina Department of Transportation, Division of Motor Vehicles Minimum Uniform Crash Criteria MinimumUniform Crash NORTH CAROLINA CRASH CRITERIA 2 | P a g e Contents Motor Vehicle Crash – A motor vehicle crash involves a motor vehicle in transport resulting in an un-stabilized situation, which includes at least one harmful event. An un-stabilized situation is a set of events not under human control, which originates when control is lost and terminates when control is regained or when all persons and property are at rest. ........................................................ 7 I. CRASH LEVEL .................................................................................................................................... 7 C1. Crash Case Identifier ................................................................................................................. 7 C2. Local Report Number ................................................................................................................ 7 C3. Crash Date .................................................................................................................................. 8 C4. Crash Time ................................................................................................................................. 8 C5. Crash County ............................................................................................................................. -

VTR-249 Standard Abbreviations for Vehicle Makes and Body Styles
Standard Abbreviations for Vehicle Makes and Body Styles Automobiles, Buses, and Light Trucks ACURA................................ACUR FERRARI............................ FERR MINI.....................................MNNI ALFA ROMEO.....................ALFA FIAT.................................... FIAT MITSUBISHI........................MITS ALL STATE.........................ALLS FISKER...............................FSKR MONARCH..........................MONA AMBASSADOR...................AMER FORD..................................FORD MORGAN............................MORG AMERICAN.........................AMER FORMERLY YUGO.............ZCZY MORRIS..............................MORR ASSEMBLED......................ASVE FRAZIER.............................FRAZ NASH..................................NASH ASTON-MARTIN.................ASTO GEO....................................GEO NISSAN...............................NISS AUBURN.............................AUBU GMC....................................GMC OLDSMOBILE.....................OLDS AUDI....................................AUDI HILLMAN.............................HILL OPEL...................................OPEL AUSTIN...............................AUST HOMEMADE.......................HMDE PACKARD...........................PACK AUSTIN-HEALY..................AUHE HONDA...............................HOND PEUGEOT...........................PEUG AUTOCAR...........................AUTO HUDSON.............................HUDS PIERCE ARROW................PRCA AVANTI...............................AVTI -

CA Safety Center
GENERAL MOTORS NORTH AMERICA Safety Center ily 28, 2000 USG 3569 Office of the Administrator National Highway Traffic Safety Administration 400 Seventh Street, SW Washington, DC 20590 Attention: Mr. George Entwistle, VIN Coordinator 4% Subject: Update of General Motors Vehicle Identification Number decoding for 2000 Model Year Dear Mr. Entwistle: Attached is the General Motors Vehicle Identification Numbering (VIN) Standard for 2000 model year, which has been updated with recent changes. This information is submitted per the VIN reporting requirements of 49 CFR Part 565.7. Revisions are indicated with a # sign in the left-hand column of the revised page, except for deletions. The following revisions have been made: Section A, page A6 - Plant code C changed from Saturn to NA LAD, Plant code Y changed from NA LAD to Saturn 0 Section B, page B3 - Carline, Series “WK” Grand Prix SEI added Section C, page C7 - Body type 6 reference to Denali changed to Yukon XL If you have any questions, please contact Thomas Braun of our Warren, Michigan office at (810) 947-1913. Safety Affairs & egulations Attachment Mail Code 480-1 1l-S56 30200 Mound Road Warren, MI 48090-9010 GENERAL MOTORS CORPORATION VEHICLE IDENTIFICATION NUMBERING STANDARD FOR 2000 MODEL YEAR VEHICLES IN COMPLIANCE WITH FEDERAL MOTOR VEHICLE SAFETY REGULATION 565 Updated - May, 2000 ALL MODEL YEARS Page i May, 2000 Corporate Information Standards GM VEHICLE IDENTIFICATION NUMBERING STANDARDS Table of Contents Page No ORGANIZATION AND DESCRIPTION OF TABLES iv TABLES OF INTERPRETIVE -

Media Information
Media Information April 9, 2020 Market overview: Compact notchback models are one of Volkswagen’s key segments in China − Volkswagen is the most popular car brand on the Chinese market. − In 2019, Volkswagen sold more than 1.6 million notchback saloons in the compact segment there, with six models to choose from − Following the COVID-19 pandemic, there are signs that the Chinese market is easing: production of vehicles and components has resumed at almost all Volkswagen sites Wolfsburg (D) – European customers love compact hatchback models like the Media contact Golf, which has spent over four decades at the top of the vehicle registration Volkswagen Communications statistics. In contrast, the world market is dominated by compact notchback Product Communications models. Worldwide, they account for almost one third of all deliveries to Christian Buhlmann Volkswagen brand’s customers – with 1.6 million vehicles sold in China alone. Head Product Line Communications Tel.: +49 5361 9-87584 A total of six models are offered there to satisfy the high demand. A market [email protected] overview of the notchback vehicles sold exclusively on the Chinese market gives a detailed insight into the differences between models. Bernd Schröder Spokesperson Product Line Compact Tel.: +49 5361 9-36867 [email protected] More at volkswagen-newsroom.com FAW-Volkswagen Bora 1) SAIC-Volkswagen Lavida 1) Spacious cabins and trunk space is important to Chinese car buyers, this is why the sedan segment is way more important than the hatchback segment. Volkswagen satisfies this need with a range of models developed exclusively for this market. -

Fuel Tanks" (Title 13, California Code of Regulations, Section 2290) for the Aforementioned Model-Year
(Page 1 of 2) State of California AIR RESOURCES BOARD EXECUTIVE ORDER A-6-537-A Relating to Certification of New Motor Vehicles GENERAL MOTORS CORPORATION Pursuant to the authority vested in the Air Resources Board by the Health and Safety Code, Division 26, Part 5, Chapter 2; and Pursuant to the authority vested in the undersigned by Health and Safety Code Sections 39515 and 39516 and Executive Orders G-45-3 and G-45-4; IT IS ORDERED AND RESOLVED: That 1992 model-year General Motors Corporation exhaust emission control systems are certified as described below for gasoline-powered passenger cars: Engine Family: N2G4. 9W8XTA7 Displacement: 4.9 Liters (297 Cu. In. ) Exhaust Emission Control Systems and Special Features: Three-Way Catalyst Oxygen Sensor Exhaust Gas Recirculation Sequential Multipoint Electronic Fuel Injection Vehicle models, transmissions, engine codes and evaporative emission control families are listed on attachments. The following are the emission standards for this engine family: Hydrocarbons Carbon Monoxide Nitrogen Oxides (Grams per Mile) (Grams per Mile) (Grams per Mile) 0. 39 7.0 0. 4 The following are the certification emission values for this engine family : Hydrocarbons Carbon Monoxide Nitrogen Oxides (Grams per Mile) (Grams per Mile) (Grams per Mile) 0. 16 2. 5 0. 2 BE IT FURTHER RESOLVED: That the listed vehicle models also comply with "California Evaporative Emission Standards and Test Procedures for 1978 and Subsequent Model Gasoline-Powered Motor Vehicles". BE IT FURTHER RESOLVED: That the listed vehicle models also comply with the Board's "Specifications for Fill Pipes and Openings of Motor Vehicle Fuel Tanks" (Title 13, California Code of Regulations, Section 2290) for the aforementioned model-year. -
RPO Codes and Descriptions
RPO Codes and Descriptions Code Description AAB MEMORY DRIVER CONVENIENCE PACKAGE AAC SHIPPED LOOSE PARTS FOR SHIPPING INSTRUCTION AAD WINDOW BODY, LEFT SIDE AAE INTERIOR TRIM DELETE AAF 2009 OEM ENGINE PHYSICAL ID AAF & PRODUCTION NUMBER 12603557 AAG MEMORY PASS CONVENIENCE PACKAGE AAH RESTRAINT KNEE, INFLATABLE, LH AAI CONTROL A/TRANS, MODE, ECONOMY/POWER AAK LOCK CONTROL, ENTRY DOOR, ELEC, KEY ACTIVATED AAL RESTRAINT KNEE, BOLSTER, LH/RH AAM RESTRAINT,KNEE BOLSTER,DRIVER AAO WINDOW ABSORBING GLAZING AAP FLEET INCENTIVE US INVESTIGATION SERVICES (D/W/3A/3Z - TRK STUX) AAP IDENTIFICATION EFFECTIVE POINT CONTROL, 2012 1/2 M.Y. AAQ ADJUSTER PASS ST POWER, 4 WAY AAR KNEE BOLSTER, FOAM TYPE AAV INTERIOR TRIM CONFIG - DELETE AAW INTERIOR TRIM CONFIG #17 AAX INTERIOR TRIM CONFIG #18 AAY INTERIOR TRIM CONFIG #16 AAZ LOCK CONTROL SIDE DOOR, VEHICLE ACCELERATION ACTIVATED AA2 WINDSHIELD,TINTED,UNSHADED AA3 DEEP TINT GLASS(REAR SIDE WINDOWS ONLY) AA4 WINDOW SPECIAL GLAZING,DOMESTIC AA5 WINDOW RR QTR - DELETE AA6 WINDOW CLEAR, ALL AA7 WINDOW,ELECTRIC OPERATED,QUICK OPENING AA7 WINDOW,POWER OPERATED,QUICK OPENING AA8 WINDOW,REAR COMPARTMENT LIFT(NOTCHBACK) ABA SEAT CONFIGURATION #1 ABB SEAT CONFIGURATION #2 ABC SEAT CONFIGURATION #3 ABD SEAT CONFIGURATION #4 ABE SEAT CONFIGURATION #5 ABF SEAT CONFIGURATION #6 ABF AIRBAG,DUAL DRIVER AND PASSENGER ABG SEAT CONFIGURATION #7 ABH SEAT CONFIGURATION #8 ABI SEAT CONFIGURATION #11 ABJ SEAT CONFIGURATION #9 ABK SEAT CONFIGURATION #10 ABM SEAT CONFIGURATION #12 ABN SENSOR OXYGEN NON-HEATED ABN SALES PACKAGE -

Tehcms) Have Been Added to the Acdelco GM Original Equipment (GM OE) Product Offering and Can Now Be Reprogrammed Without Relying on the Dealer
REPROGRAM IT YOURSELF Transmission Electro Hydraulic Control Modules (TEHCMs) have been added to the ACDelco GM Original Equipment (GM OE) product offering and can now be reprogrammed without relying on the dealer. TEHCMs, which are found in all GM 6-speed automatic transmissions, can be flashed at your facility using the ACDelco TIS2Web program and a J2534 interface tool, making it even easier to earn customers’ trust. INSTALL AN ACDELCO GM OE TEHCM ASSOCIATED PARTS FOR TEHCM REPLACEMENT FOR OPTIMAL DRIVEABILITY AND DURABILITY TEHCM replacements require Dexron VI Transmission New TEHCMs integrate electronic and hydraulic Oil and the following parts based on application. components into a single module and are backed 6T30/40/45/50 Applications by a 12-month/12,000-mile limited warranty. The Valve Body Cover Gasket , part # 24234281 latest TEHCM hardware includes a filter plate, solenoids and an upgraded frame. 6T70/75 Applications Valve Body Cover Gasket, part # 24229593 6L45/50 Applications Seal Kit, part # 24238913 A/Trans Fluid Pan Gasket, part # 24225800 6L80 Applications Seal Kit, part # 24236927 A/Trans Fluid Pan Gasket, part # 24224781 6L90 Applications Seal Kit, part # 24236927 A/Trans Fluid Pan Gasket, part # 24226850 ACDelco TEHCMs Advantages New GM OE module Optimized fuel economy Download the latest calibration software Smooth shifts Used, Counterfeit and Aftermarket Modules Disadvantages May not include the latest calibration updates Potential shift issues and reduced fuel economy ©2015 General Motors. All rights