DOCSLIB.ORG

Provided for Non-Commercial Research and Educational Use Only. Not for Reproduction Or Distribution Or Commercial Use

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Provided for Non-Commercial Research and Educational Use Only. Not for Reproduction Or Distribution Or Commercial Use Provided for non-commercial research and educational use only. Not for reproduction or distribution or commercial use. This article was originally published by IWA Publishing. IWA Publishing recognizes the retention of the right by the author(s) to photocopy or make single electronic copies of the paper for their own personal use, including for their own classroom use, or the personal use of colleagues, provided the copies are not offered for sale and are not distributed in a systematic way outside of their employing institution. Please note that you are not permitted to post the IWA Publishing PDF version of your paper on your own website or your institution’s website or repository. Please direct any queries regarding use or permissions to [email protected] 36 © IWA Publishing 2014 Journal of Water and Climate Change | 05.1 | 2014 Development of HydroClimatic Conceptual Streamflow (HCCS) model for tropical river basin Parag P. Bhagwat and Rajib Maity ABSTRACT Combined processes of land-surface hydrology and hydroclimatology influence the response of a Parag P. Bhagwat Rajib Maity (corresponding author) watershed to different hydroclimatic variables. In this paper, streamflow response of a watershed to Department of Civil Engineering, Indian Institute of Technology Kharagpur, hydrometeorological variables is investigated over a part of two tropical Indian rivers – Narmada and Kharagpur 721302, fl West Bengal, Mahanadi. The proposed HydroClimatic Conceptual Stream ow (HCCS) model is able to consider the India time-varying basin characteristics and major hydrologic processes to model basin-scale streamflow E-mail: [email protected]; [email protected] using climate inputs at a daily scale. In addition, the proposed model is able to provide additional overall estimates of ground water recharge component and evapotranspiration component from the entire basin. Moreover, ability to consider the time-varying watershed characteristics and hydroclimatic inputs renders the proposed model usable for assessment of future streamflow variation. This application is also investigated for both the study basins. In general, the methodological approach of the proposed model can be applied to other tropical basins for daily streamflow modelling as well as future streamflow assessment. Key words | climate, conceptual model, hydroclimatology, prediction, streamflow INTRODUCTION In the context of a changing climate, identification of stream- better or at least comparable performance to existing flow response to other hydroclimatological variables is a approaches. research challenge (Kumar & Maity ; Maity & Kashid ). Most of the existing approaches attempt to consider Background and literature review and conceptualize different hydrological processes. How- ever, time varying watershed characteristics are not A brief review (with respect to the huge amount of literature considered. As a consequence, consistency (decadal to cli- available) of existing approaches reveals that the hydrologi- matic scale) of the model performance is affected under a cal models for streamflow estimation can be grouped into changing climate and changing watershed characteristics three broad categories viz: (a) physically based models, (b) that are not accounted for. Here lies the importance of this conceptual models, and (c) artificial intelligence (AI)-based study since recent observation of climate change has added models. In physically based models, existing knowledge of a new dimension towards this overall research direction in all possible hydrological processes is represented through hydrologic modelling. The question examined was, is it poss- a set of mathematical equations. Examples of some popular ible to model watershed response as streamflow with the physically based models include System Hydrologique Euro- simultaneous consideration of changing climate and time pean (Abbott et al. a,b), Better Assessment Science varying watershed characteristics? As such, it was found Integrating point and Non-point Sources (EPA ), Soil that there is a need to develop a streamflow model having and Water Assessment Tool (SWAT) (Eckhardt & Arnold few parameters, which will be able to consider time varying ; Grizzetti et al. ), and Community Land Model watershed characteristics and climatic inputs, and provide (Lawrence et al. ). However, an inability for accurate doi: 10.2166/wcc.2013.015 37 P. P. Bhagwat & R. Maity | HydroClimatic Conceptual Streamflow model Journal of Water and Climate Change | 05.1 | 2014 mathematical representation of hydrological processes con- properties of the watershed. As a consequence, the outcome sidering the huge spatial variability, computational demands of such models sometimes becomes crude. Sometimes, even and overparameterization effects, and non-availability of the major components, such as evapotranspiration, ground required comprehensive data sets make the results of phys- water recharge component and streamflow, are not separ- ically based models poor in many cases (Piotrowski & ated from each other. Moreover, typical absence of short- Napiorkowski ; Zeng et al. ). term (i.e., fortnight to seasonal) and/or long-term (i.e., deca- Conceptual models are also derived using (relatively dal to centennial) dynamic characteristics raise questions simpler) mathematical equations, which mainly consider against its applicability to capture the dynamic, time-varying the major hydrological process of the complex hydrological response of watershed to long-term climate change impact cycle, which is difficult to understand fully. However, in the analysis studies, which are particularly essential in a chan- absence of complete knowledge, they may be represented in ging climate. a simplified way by means of the system concept. A system is AI-based models are much simpler with respect to the a set of connected parts that form the whole. By using the understanding of underlying physical processes. These system concept, effort is directed to the construction of a models are developed based on interrelationships between model relating inputs and outputs rather than to the extre- input and output values of the concerned variables. In the mely difficult task of exact representation of the system last two decades, use of AI-based models has increased due details, which may not be significant from a practical point to their lower dependence on physical understanding of the of view or may not be known. Nevertheless, knowledge of underlying process(es) by the users, and provide quick as the physical system helps in developing a conceptually well as reasonably impressive results compared with the clear model. The major hydrological processes considered other two types of models discussed before. Some of the are mostly rainfall, evapotranspiration, infiltration, surface most popular AI-based models, which are applied to hydrolo- runoff, etc., which have significant importance towards the gical modelling, are based on artificial neural network (Kumar watershed output. As mentioned before, the physically et al. ), genetic programming (Maity & Kashid ), and based models require a large number of data and still pro- support vector machines (SVMs). However, apart from the cri- duce poor results due to a variety of reasons. Hence, ticism of the ‘black-box’ nature, the performance of such conceptual models are used as alternative models for water- models is often found to be excellent and difficult to replicate sheds. Some of the generally used conceptual models are the using other conceptual/physically based approaches. This Stanford watershed model, which is an early finding in con- said, the same criticism which was mentioned in the case of ceptual hydrological modelling by Crawford & Linsley conceptual models earlier, exists for such modelling (), the Institute Royal Meteorology Belgium (IRMB) approaches as well. That is, due to their static nature, studies model (Bultot & Dupriez ), HYDROLOG model related to long-term climate change impact analysis may not which was later modified by Chiew & McMahon () to be always possible with this modelling approach. the MODifed HYDROLOG (MODHYDROLOG) model, Hydrologiska Byråns Vattenbalansavdelning (HBV) model Motivation and objectives which was developed at the Swedish Meteorological and Hydrological Institute (SMHI) in 1972 (Bergström ), Specifically, this study attempts to develop a basin-scale and the Hydrologic Simulation Program-FORTRAN model daily hydroclimatic streamflow model (named as HydroCli- which is a modified version of Stanford model (Johnson matic Conceptual Streamflow (HCCS) model), considering et al. ), and so on. These models are designed to the time-varying watershed characteristics and major hydro- approximate the general hydrological processes, which dic- logic processes to model basin-scale streamflow using tate the hydrological cycle. However, most of the climate inputs. The developed modelling approach is con- conceptual models consider all hydrological processes to ceptual in nature. Its performance is investigated for two be lumped together, greatly simplify the hydrological pro- Indian tropical river basins. Performances of AI-based cesses involved, and do not consider time-varying machine learning approaches are found to overshadow the 38 P. P. Bhagwat & R. Maity | HydroClimatic Conceptual Streamflow model Journal of Water and Climate Change | 05.1 | 2014 performance of other modelling approaches. Thus, the per- dependent. The proposed methodology is motivated by formance of the proposed model is compared with the SACramento
Load more

Recommended publications
  • Impact of Climate Change on Water Resources in Madhya Pradesh
    Impact of Climate Change on Water Resources in Madhya Pradesh Impact of Climate Change on Water Resources in Madhya Pradesh Impacts of Climate Change on Water Resources in Madhya Pradesh - An Assessment Report This report is prepared under the financial support by Department for International Development (DFID) for the project Strengthening Performance Management in Government (SPMG) being implemented in Madhya Pradesh state of India. SPMG is an initiative of Department for International Development (DFID) to provide assistance to Government of Madhya Pradesh for strengthening planning and governance systems. One of the key focus areas of SPMG is to ensure environmental sustainability and climate compatible development in the state. As part of this initiative, Development Alternatives (DA) is recognized by Government of MP and DFID to provide technical support to Madhya Pradesh State Knowledge Management Centre on Climate Change (SKMCCC), EPCO. DA is assisting SKMCCC in facilitating integration of climate change concerns into departmental activities and plans, through strengthening technical capacities and generating strategic knowledge. Authors Dr. K.P Sudheer, Indian Institute of Technology, Madras Overall Guidance Mr. Anand Kumar, Ms. Harshita Bisht, Ms. Rowena Mathew, Development Alternatives (DA) Shri Ajatshatru Shrivastava, Executive Director, EPCO Mr. Lokendra Thakkar, Coordinator, State Knowledge Management Center on Climate Change, EPCO Acknowledgement We place on record our gratitude to the Department for International Development (DFID) for providing the financial and institutional support to this task and State Knowledge Management Centre on Climate Change (SKMCCC), EPCO, Government of Madhya Pradesh for their strategic guidance. Development Alternatives acknowledge the scientific expertise of Dr. K.P Sudheer from Indian Institute of Technology, Madras, for contributing in developing the impact assessment report.
    [Show full text]
  • Seismic Hazard Estimation for Rani Avanti Bai Sagar Project at Bargi
    International Journal of Civil Engineering and Technology (IJCIET) Volume 8, Issue 7, July 2017, pp. 78–87, Article ID: IJCIET_08_07_009 Available online at http:// http://iaeme.com/Home/issue/IJCIET?Volume=8&Issue=7 ISSN Print: 0976-6308 and ISSN Online: 0976-6316 © IAEME Publication Scopus Indexed SEISMIC HAZARD ESTIMATION FOR RANI AVANTI BAI SAGAR PROJECT AT BARGI Rakesh Kumar Grover Associate Professor, Department of Civil Engineering, Jabalpur Engineering College, Jabalpur (M.P.), India Dr. R. K. Tripathi Professor, Department of Civil Engineering, National Institute of Technology, Raipur (C.G.) India Dr. Rajeev Chandak Professor & Head, Deparment of Civil Engineering, Jabalpur Engineering College, Jabalpur (M.P.), India Dr. H. K. Mishra Principal, Indira Gandhi Engineering College, Sagar, (M.P.) India ABSTRACT Rani Avanti Bai Sagar Project at Bargi is a multipurpose project in the state of Madhya Pradesh (India). In this study seismic hazard has been estimated for Bargi Dam site. The probabilistic Seismic Hazard analysis has been used. Effects of all the faults, which can produce earthquake equal to or more than 3.5 Magnitude and those within a radius of 300 Km from the centre of the Masonry Dam has been considered. The past history of earthquakes indicated that a total 82 earthquakes, of magnitude 3.5 or more has been occurred in last 175 years. The maximum magnitude reported within the region of consideration is 6.5 in 1927 at Umaria. Probabilistic approach use these data for hazard Analysis. Results are presented in the form of peak ground acceleration and seismic hazard curves. Key words: Peak Ground Acceleration, Ground Motion, Bargi Dam, Seismic Hazard, Psha Cite this Article: Rakesh Kumar Grover, Dr.
    [Show full text]
  • The Omkareshwar Dam in India : Closing Doors on Peoples' Future
    The Omkareshwar Dam in India : Closing Doors on Peoples’ Future Abstract: The Omkareshwar Project is one of 30 large dams to be built in the Narmada Valley and which are being contested by one of India’s strongest grassroots movements. In Spring 2004 MIGA, the World Bank’s Investment Guarantee Agency, turned down an application for Omkareshwar because of “environmental and social concerns”. The project will displace 50,000 small farmers and flood up to 5800 hectars of one of Central India’s last intact natural forests. Construction of the dam was taken up in November 2003, in spite of the fact that no Environmental Impact Asessment and no resettlement plan has been prepared for the project. The project violates a number of national and international standards, including the so-called Equator Principles. Although it has been turned down by Deutsche Bank, several foreign banks and export credit agencies are still considering loan and insurance applications for Omkareshwar. Village Sukwa, Omkareshwar submergence area A number of European private banks and several Export Credit Agencies (ECAs) have been asked to provide support for the highly controversial Omkareshwar Dam Project in India. In November 2003, representatives of the Japan Center for Sustainable Environment and Society (JACSES) and the German environment and human rights NGO Urgewald undertook a fact-finding mission to the Omkareshwar area. The following report is based on data collected during our visit as well as discussions with the project sponsor, affected villagers and a review of all obtainable project documents. The Project and its Sponsor The Omkareshwar Project was conceived in 1965 as an irrigation and power dam to be built in the Central Indian State of Madhya Pradesh.
    [Show full text]
  • Riverine Ecology and Fisheries •
    Riverine ecology and fisheries •.. vis-a-vis hydrodynamic alterations: Impacts and remedial measures V. Pathak and R. K. Tyagi Bull. No. - 161 January - 2010 Central Inland Fisheries Research Institute (Indian Council of Agricultural Research) Barrackpore, Kolkata - 700120, West Bengal Riverine ecology and fisheries vis-a-vis hydrodynamic alterations: Impacts and remedial measures v. Pathak and R.K. Tyagi ISSN 0970-616X © 2009 Material contained in this Bulletin may not be reproduced, in any form, without the permission of the publisher Published by : Director, CIFRI,Barrackpore Edited By: Dr. P.K. Katiha Dr. R. K. Manna The Agricultural Economics Section and Project Monitoring and Documentation Cell, CIFRI,Barrackpore ) Printed at Eastern Printing Processor 93, Dakshindari Road, Kolkata - 48 90Vlf/(,/l/vYl/1!/ I!/DCPtCP'f'f (//Yl/d ?vSlIvI!/'I/VMy IContents subjects Page No. Foreword List of tables Hi List of figures Hi Introduction 1 Classification of rivers 1 Ecological status of rivers 4 Himalayan rivers Ganga 4 Ravi 5 Sutlej 5 Beas 5 Brahmaputra 7 Peninsular rivers Mahanadi 7 Godavari 8 Krishna 8 Cauvery 8 Narmada 9 Rate of energy transformation by producers 11 and fish production potential of rivers Fish fauna 13 Himalayan rivers 13 Peninsular rivers 18 90UIP(!/"I/U/1/f!/ f!/Cdyt<Y'F1f O//1/J ?us-/vf!/'I/Uf!/!v suifects Page No. Fishery 23 Himalayan rivers The Indus river system 23 Ganga 24 Brahmaputra 26 Peninsular rivers Mahanadi 27 Godavari 28 Krishna and Cauvery 29 Narmada 29 Tapti 30 Factors influencing fish production from rivers 30 Hydrological regimes 30 Environmental degradation 31 Fishing pressure 32 Conservation measures 34 90vlf/e/l/v/1/l!/ l!/C/{Yt{YfJ'1f (II/1/d fV!Y/vl!/'l/Vl!/!Y IForeword The vast network of Indian rivers and rivulets has been source for rich fish biodiversity, lucrative fishery and provide livelihood to countless riparian fishers.
    [Show full text]
  • Aquatic Phyto-Biodiversity of Bargi Dam Catchment Area at Jabalpur, IJCRR Section: Healthcare Sci
    International Journal of Current Research and Review Life Science DOI: 10.7324/IJCRR.2018.1049 Aquatic Phyto-Biodiversity of Bargi Dam Catchment Area at Jabalpur, IJCRR Section: Healthcare Sci. Journal Madhya Pradesh: An Appraisal Impact Factor 4.016 ICV: 71.54 Dharmendra Kumar Parte1, S. D. Upadhyaya2, R. P. Mishra3, C. P. Rahangdale4, Sajad Ahmad Mir5, Anu Mishra6 1Research Scholar at RDVV Jabalpur; 2Prof. and Head Department of Forestry JNKVV Jabalpur, MP, India; 3Prof. at Department of Biological Sciences RDVV Jabalpur; 4SRF, ISRO Project Department of Plant Physiology JNKVV Jabalpur, MP, India; 5Research Scholar at Department of Biological Sciences RDVV Jabalpur; 6JRF at JNKVV Jabalpur, MP, India. ABSTRACT Aim: The study was conducted on Bargi Dam catchment area at Jabalpur district of Madhya Pradesh with the objective of De- termining “The Aquatic species Floristic Composition Diversity and the Vegetation Structure of the Aquatic Plants Communities in the Bargi Dam Catchment Area”. Methodology: Random sampling method was used to collect the vegetation data according to 36 plots of per quadrates 10m x10m size. Results: A total of 119 species belonging to 79 genera and 39 families were recorded during the survey in which emergent 61%, marshy land 21%, free floating 9%, rooted floating 1%, submerged 8% aquatic plants were identified from the Bargi Dam catchment area. Key Words: Wetland, Catchment, Floristic composition, Aquatic plants INTRODUCTION are key components for the well-functioning of wetland eco- system for biological productivity, supporting diverse com- Aquatic ecosystems play an important role in human life. munity of ecosystem by providing lots of goods and services.
    [Show full text]
  • Narmada Control Authority Presentation
    National Level Three Day Programme on Best Practices in Water Resources Sector 26-28 October,2017 at APHRDI,Bapatla Narmada Control Authority - Transforming Conflict into Cooperation amongst riparian States by Dr. MUKESH KUMAR SINHA EXECUTIVE MEMBER, NARMADA CONTROL AUTHORITY MINISTRY OF WATER RESOURCES, RIVER DEVELOPMENT & GANGA REJUVENATION Government of India 1 Narmada River Fifth Largest River Of India Largest West Flowing River River Length - 1312 km (from Amarkantak to Arabian Sea) Catchment Area - 98,000 km2 Mean Annual Rainfall - 1,180 mm Average Annual Run-Off - 41,000 MCM (33.21 MAF) 2 NARMADA RIVER BASIN - 30 Major Projects, 135 Medium Projects and over 3000 Minor Schemes Narmada Main Canal Indira Sagar Dam Bargi Dam Sardar Sarovar Dam Omkareshwar Dam Maheshwar Dam 3 Narmada Water Disputes Tribunal Constituted by Govt. of India under Section 4 of the Inter-State Water Disputes Act, 1956 through notification no. SO 4054 dated 6th October, 1969, to adjudicate the water dispute between the States of Gujarat, Madhya Pradesh, Maharashtra and Rajasthan over the use, distribution and control of the waters of the inter-state river Narmada. On 16 August 1978, the Tribunal declared its Award under Section 5(2) read with Section 5(4) of the Inter-State Water Disputes Act, 1956. Thereafter, references were filed by the Union of India and the States of Gujarat, Madhya Pradesh, Maharashtra and Rajasthan respectively under Section 5(3) of the Inter-State Water Disputes Act, 1956. These references were heard by the Tribunal and on 7 December 1979 gave its final order. The same was published in the extraordinary Gazette by the Government of India on 12 December 1979.
    [Show full text]
  • Full Case Study (Pdf)
    ABSTRACT Case Title: India: A tale of rehabilitation of people displaced due to dam construction (#250) Subtitle: Describes the process of rehabilitating people displaced due to construction of the Bargi Dam, from initial agitations to eventual resolution of conflict. Description The construction of the Bargi Dam (1971-1990) on the river Narmada affected 27432 ha of land and displaced 5,475 families. Initially provision was made only for payment of compensation for land and property. The lack of planning for human problems led eventually to an agitation lasting over several years. On receiving complaints from the affected people the Commissioner of Social Welfare intervened in 1986 and convinced the state to prepare a rehabilitation plan of Rs.100 million (US$ 2 million). Delay and mismanagement, including rehabilitation work in places not affected by the dam, led to the displaced people coming together to form a Union. Demonstrations began in 1992, demanding fishing rights and protesting against the complete filling up of the dam. In 1994, the Chief Minister met the displaced people, accepted responsibility for rehabilitation, and agreed to some of the demands. To speed up the works, a divisional level planning committee was set up which drew up a rehabilitation plan, but its implementation was held up due to delays in obtaining funding. In 1996, violent demonstrations resumed demanding reduction of the reservoir water level. The Chief Secretary visited the affected area, met the Union, and agreed to demands. The cycle of non-implementation, agitation and subsequent agreement to some demands was repeated in 1997. Since then rehabilitation work has been carried out in cooperation between the Union and the government.
    [Show full text]
  • The Sardar Sarovar Dam Project: Selected Documents Level
    Chapter 1 The Sardar Sarovar Dam Project: An Overview Philippe Cullet The Sardar Sarovar Project (SSP) is part of a gigantic scheme seeking to build more than 3,000 dams, including 30 big dams, on the river Narmada, a 1,312 km river flowing westwards from Amarkantak in Madhya Pradesh, touching Maharashtra and ending its course in Gujarat. The SSP is a multi-purpose dam and canal system whose primary rationale is to provide irrigation and drinking water. Power generation is another expected benefit. It is the second biggest of the proposed dams on the Narmada, and its canal network is projected to be the largest in the world. The dam is situated in the state of Gujarat, which will derive most of the benefits of the project, but the submergence – 37,533 hectares in total – is primarily affecting the state of MP (55 per cent) and to a much lesser extent the state of Maharashtra. The SSP has been one of the most debated development projects of the past several decades in India and at the international level. It is only one of many similar big projects in the Narmada valley and in India generally but it has acquired a symbolic status in development debates. This is due in part to the complexity of such multi-purpose projects and the multiple positive and negative impacts associated with big dams. This is also due to the specificities of this project, which was first proposed nearly 60 years ago. Firstly, the fact that this project involves four states – Gujarat, MP, Maharashtra and Rajasthan – with the state of Gujarat receiving most of the benefits of the project has repeatedly led to disagreements among the concerned states.
    [Show full text]
  • General-STATIC-BOLT.Pdf
    oliveboard Static General Static Facts CLICK HERE TO PREPARE FOR IBPS, SSC, SBI, RAILWAYS & RBI EXAMS IN ONE PLACE Bolt is a series of GK Summary ebooks by Oliveboard for quick revision oliveboard.in www.oliveboard.in Table of Contents International Organizations and their Headquarters ................................................................................................. 3 Organizations and Reports .......................................................................................................................................... 5 Heritage Sites in India .................................................................................................................................................. 7 Important Dams in India ............................................................................................................................................... 8 Rivers and Cities On their Banks In India .................................................................................................................. 10 Important Awards and their Fields ............................................................................................................................ 12 List of Important Ports in India .................................................................................................................................. 12 List of Important Airports in India ............................................................................................................................. 13 List of Important
    [Show full text]
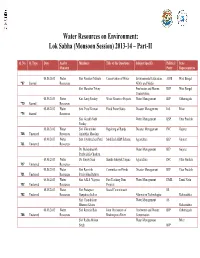
  • Water Resources on Environment: Lok Sabha (Monsoon Session) 2013-14 – Part-II
    Water Resources on Environment: Lok Sabha (Monsoon Session) 2013-14 – Part-II Q. No. Q. Type Date Ans by Members Title of the Questions Subject Specific Political State Ministry Party Representative 08.08.2013 Water Shri Narahari Mahato Conservation of Water Environmental Education, AIFB West Bengal *67 Starred Resources NGOs and Media Shri Manohar Tirkey Freshwater and Marine RSP West Bengal Conservation 08.08.2013 Water Km. Saroj Pandey Water Resource Projects Water Management BJP Chhattisgarh *70 Starred Resources 08.08.2013 Water Smt. Putul Kumari Flood Prone States Disaster Management Ind. Bihar *74 Starred Resources Shri Gorakh Nath Water Management BSP Uttar Pradesh Pandey 08.08.2013 Water Shri Vikrambhai Repairing of Bunds Disaster Management INC Gujarat 708 Unstarred Resources Arjanbhai Maadam 08.08.2013 Water Smt. Jayshreeben Patel Modified AIBP Scheme Agriculture BJP Gujarat 711 Unstarred Resources Dr. Mahendrasinh Water Management BJP Gujarat Pruthvisinh Chauhan 08.08.2013 Water Dr. Sanjay Sinh Sharda Sahayak Yojana Agriculture INC Uttar Pradesh 717 Unstarred Resources 08.08.2013 Water Shri Ramsinh Committee on Floods Disaster Management BJP Uttar Pradesh 721 Unstarred Resources Patalyabhai Rathwa 08.08.2013 Water Shri A.K.S. Vijayan Fast Tracking Dam Water Management DMK Tamil Nadu 722 Unstarred Resources Projects 08.08.2013 Water Shri Prataprao Social Commitment SS 752 Unstarred Resources Ganpatrao Jadhav Alternative Technologies Maharashtra Shri Chandrakant Water Management SS Bhaurao Khaire Maharashtra 08.08.2013 Water
    [Show full text]
  • Madhya Pradesh: Geography Contents
    MPPSCADDA Web: mppscadda.com Telegram: t.me/mppscadda WhatsApp/Call: 9953733830, 7982862964 MADHYA PRADESH: GEOGRAPHY CONTENTS ❖ Chapter 1 Introduction to Geography of Madhya Pradesh ❖ Chapter 2 Physiographic Divisions of Madhya Pradesh ❖ Chapter 3 Climate Season and Rainfall in Madhya Pradesh ❖ Chapter 4 Soils of Madhya Pradesh ❖ Chapter 5 Rivers and Drainage System of Madhya Pradesh ❖ Chapter 6 Major Irrigation and Electrical Projects of Madhya Pradesh ❖ Chapter 7 Forests and Forest Produce of Madhya Pradesh ❖ Chapter 8 Biodiversity of Madhya Pradesh CONTACT US AT: Website :mppscadda.com Telegram :t.me/mppscadda WhatsApp :7982862964 WhatsApp/Call :9711733833 Gmail: [email protected] FREE TESTS: http://mppscadda.com/login/ Web: mppscadda.com Telegram: t.me/mppscadda WhatsApp/Call: 9953733830, 7982862964 INTRODUCTION TO GEOGRAPHY OF MADHYA PRADESH MPPSCADDA Web: mppscadda.com Telegram: t.me/mppscadda WhatsApp/Call: 9953733830, 7982862964 1. INTRODUCTION TO GEOGRAPHY OF MADHYA PRADESH Topography of Madhya Pradesh • Madhya Pradesh is situated at the north-central part of Peninsular plateau India, whose boundary can be classified in the north by the plains of Ganga-Yamuna, in the west by the Aravalli, east by the Chhattisgarh plain and in the south by the Tapti Valley and the plateau of Maharashtra. • Geological Structure: Geologically MP is a part of Gondwana Land. 3,08,252 km2 Area (9.38% of the total area of India) 21⁰ 6' - 26 ⁰30' Latitudinal Expansion 605 km (North to South) 74⁰ 59' - 82 ⁰66' Longitudinal Expansion 870 km (East to West) Width is more than Length Indian Standard Meridian Singrauli District ( Only one district in MP) 82⁰30' passes • Topic of Cancer and Indian Standard Meridian do not cross each other in any part of MP Geographical Position of MP • Madhya Pradesh is the 2nd (second) largest state by area with its area 9.38% of the total area of the country.
    [Show full text]
  • Assessment of Impact of Lockdown on Water Quality of Major Rivers
    MONITORING OF INDIAN NATIONAL AQUATIC RESOURCES SERIES (MINARS) MINARS/38/2020-21 Assessment of Impact of Lockdown on Water Quality of Major Rivers CENTRAL POLLUTION CONTROL BOARD Ministry of Environment, Forest & Climate Change Parivesh Bhawan, East Arjun Nagar DELHI-110032 Website : www.cpcb.nic.in Septemeber 23, 2020 Assessment of Impact of Lockdown on Water Quality of Major Rivers CENTRAL POLLUTION CONTROL BOARD Ministry of Environment, Forest & Climate Change Parivesh Bhawan, East Arjun Nagar DELHI-110032 Website : www.cpcb.nic.in ABBREVIATIONS BOD - Biochemical Oxygen Demand COD - Chemical Oxygen Demand CPCB - Central Pollution Control Board CWC - Central Water Commission DO - Dissolved Oxygen FC - Fecal Coliform GoI - Government of India GPI - Grossly Polluting Industries Km - Kilometre MLD - Million Litres per day MoEF & CC - Ministry of Environment, Forest and Climate Change NABL - National Accreditation Board for Testing and Calibration Laboratories NWMP - National Water Quality Monitoring Programme PCCs - Pollution Control Committees RTWQMS - Real Time Water Quality Monitoring Station SPCBs - State Pollution Control Boards TPD - Tonnes per day WHO - World Health Organisation C O N T R I B U T I O N S Overall Guidance: Shri Shiv Das Meena (IAS), Chairman, CPCB Overall Supervision: Dr. Prashant Gargava, Member Secretary, CPCB Report Finalisation: Shri. A. Sudhakar, Scientist ‘E’ & DH, WQM-I Division Shri. J. Chandra Babu, Scientist ‘E’, WQM-I Division Data Validation and Analysis: Mrs. Suniti Parashar, Scientist ‘C’ Report Preparation: Mrs.Alpana Narula, SSA Dr. Pooja Tripathi, RA Dr. Khyati Mittal, RA Ms. Deepty Goyal, SRF Ms. Deepa Kumari, JRF Mrs. Meetali Sharma, Taxonomist Data Compilation and Maps Preparation: Shri. Pawan Tripathi, GIS Expert Shri.
    [Show full text]