DOCSLIB.ORG

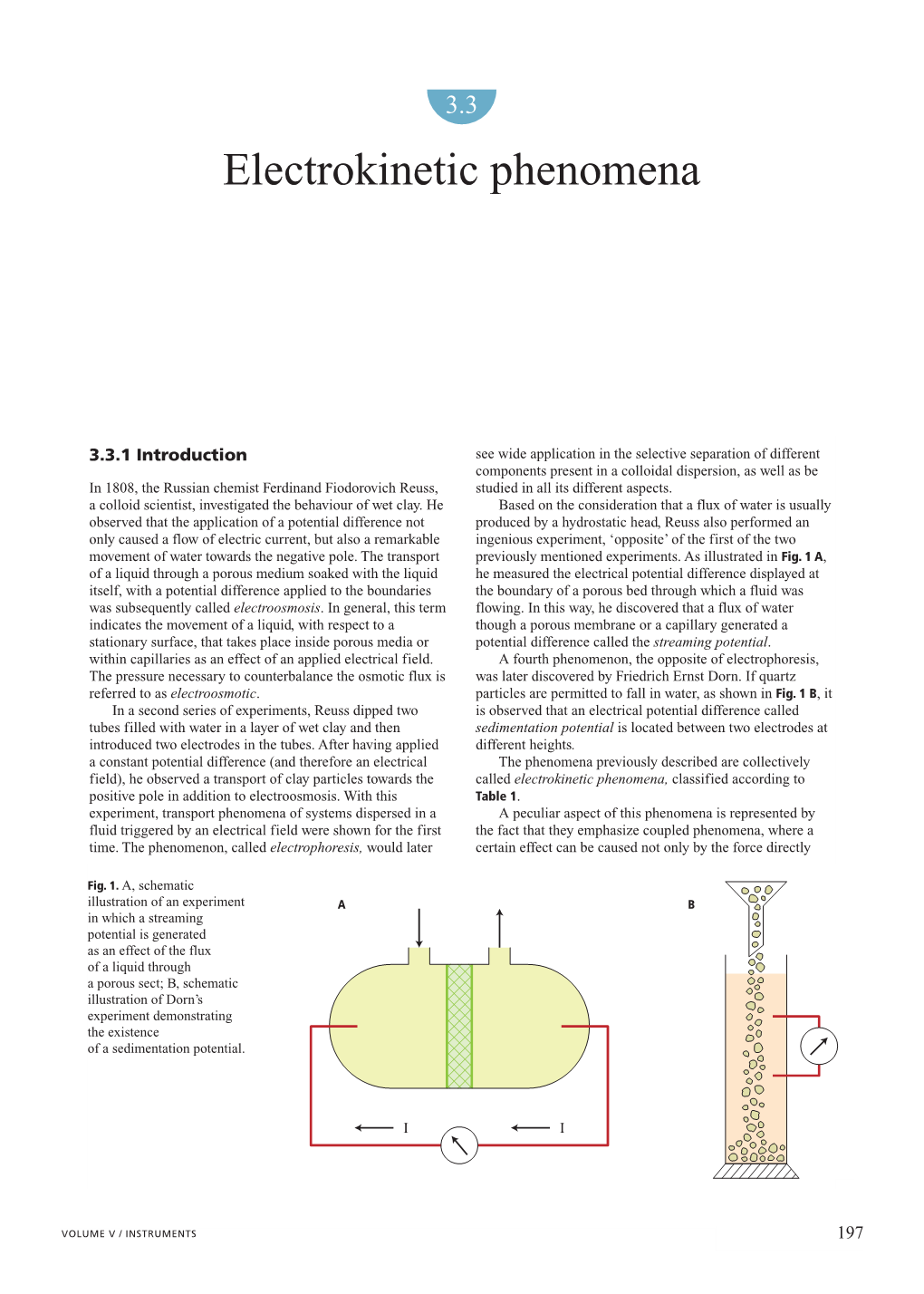
Electrokinetic Phenomena

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Electrokinetic Phenomena 3.3 Electrokinetic phenomena 3.3.1 Introduction see wide application in the selective separation of different components present in a colloidal dispersion, as well as be In 1808, the Russian chemist Ferdinand Fiodorovich Reuss, studied in all its different aspects. a colloid scientist, investigated the behaviour of wet clay. He Based on the consideration that a flux of water is usually observed that the application of a potential difference not produced by a hydrostatic head, Reuss also performed an only caused a flow of electric current, but also a remarkable ingenious experiment, ‘opposite’ of the first of the two movement of water towards the negative pole. The transport previously mentioned experiments. As illustrated in Fig. 1 A, of a liquid through a porous medium soaked with the liquid he measured the electrical potential difference displayed at itself, with a potential difference applied to the boundaries the boundary of a porous bed through which a fluid was was subsequently called electroosmosis. In general, this term flowing. In this way, he discovered that a flux of water indicates the movement of a liquid, with respect to a though a porous membrane or a capillary generated a stationary surface, that takes place inside porous media or potential difference called the streaming potential. within capillaries as an effect of an applied electrical field. A fourth phenomenon, the opposite of electrophoresis, The pressure necessary to counterbalance the osmotic flux is was later discovered by Friedrich Ernst Dorn. If quartz referred to as electroosmotic. particles are permitted to fall in water, as shown in Fig. 1 B, it In a second series of experiments, Reuss dipped two is observed that an electrical potential difference called tubes filled with water in a layer of wet clay and then sedimentation potential is located between two electrodes at introduced two electrodes in the tubes. After having applied different heights. a constant potential difference (and therefore an electrical The phenomena previously described are collectively field), he observed a transport of clay particles towards the called electrokinetic phenomena, classified according to positive pole in addition to electroosmosis. With this Table 1. experiment, transport phenomena of systems dispersed in a A peculiar aspect of this phenomena is represented by fluid triggered by an electrical field were shown for the first the fact that they emphasize coupled phenomena, where a time. The phenomenon, called electrophoresis, would later certain effect can be caused not only by the force directly Fig. 1. A, schematic illustration of an experiment AB in which a streaming potential is generated as an effect of the flux of a liquid through a porous sect; B, schematic illustration of Dorn’s experiment demonstrating the existence of a sedimentation potential. II VOLUME V / INSTRUMENTS 197 SURFACES AND DISPERSE SYSTEMS Table 1. Classification of electrokinetic phenomena Electrical forces Mechanical forces solid at rest solid in motion solid at rest solid in motion electroosmosis electrophoresis streaming potential sedimentation potential applied to it (for instance, the current generated by an solid and a liquid phase. As such, they apply to systems electrical field), but also by forces associated with different where the ratio is high between the interphase area and the effects (for instance, an electric current caused by a pressure volume, such as capillaries and porous materials soaked in difference which typically generates a fluid flow). An liquids or dispersions of solid particles in a liquid. In fact, important confirmation of this aspect emerged 20 years after electrokinetic processes are due to the opposite charges on Reuss experiments when another group of phenomena was the solid particles and in the liquid. On the solid, the charge discovered presenting the same type of coupling: is generated by the presence of ions on the surface due to thermoelectric phenomena. In particular, Thomas Johann either their selective adsorption from the solution or the Seebek observed that by heating the ends of a bimetallic ionization of molecules present on the surface itself. These couple at different temperatures, an electrical potential phenomena do not arise in liquids characterized by small difference was generated, whereas Jean-Charles-Athanase values of the dielectric constant, such as chloroform, Peltier noticed that, inversely, a current transport through the diethylether and carbon disulphide. On the other hand, these couple caused a heat transfer from one junction to the other. phenomena are observed in polar liquids such as acetone, This group of phenomena found a descriptive frame alcohols and especially water. within the context of thermodynamics of irreversible At the boundary, there is a segregation of positive or processes. In order to illustrate this aspect, we will refer to negative electric charges perpendicular to the surface itself. the motion of a fluid (for instance, water) through a porous For example, on a silica surface in contact with an aqueous sect or a membrane, expressing the fluxes of electrical solution, there are some hydroxylic groups, derived from charges and of water molecules through the current intensity SiO2 hydration, that forms silic acid. This compound causes I and the water volumetric flux JV . Their coupling can be the following ionic dissociation: described by the following relationships: ᭤ 2−+ Ϫ᭣ + HSiO23Ϫ SiO 3 2H [1] IL=+∆∆ϕ LP 11 12 producing negative charges on the surface that exert an [2] =+∆∆ϕ JLV 21 LP 22 attractive action on hydrogen ions in the solution, forming an where Df indicates the electrical potential difference and electric double layer (Fig. 2). Another example is silver DP the hydrostatic potential difference, whereas parameters L , L , L , L are the phenomenological parameters. The ϩ 11 22 12 21 H ϩ ϩ Onsager reciprocity relationship is applied to the mixed H H Hϩ ϩ terms L describing coupling by assuming L ϭL . From H ϩ ij 12 21 2Ϫ 2Ϫ H 2Ϫ these expressions, it is possible to notice that even if no SiO3 SiO3 SiO3 potential difference is applied (i.e. if Dfϭ0), then simply the presence of a pressure difference can produce an electric SiO2 current. On the other hand, if no pressure difference is applied, the presence of an electromotive force can still generate a water flux by electroosmosis. Moreover the A following relationships are valid: I J ϩ [3] ==L V = L H ϩ ∆∆P 12 ϕ 21 H ∆ϕ =0 ∆P=0 ϩ ϩ ϩ H H 2Ϫ H ϩ Actually, when other information is unavailable, the SiO3 H Ϫ Ϫ previous equations are also unable to provide the amount of SiO2 SiO2 3 3 ϩ electric or volumetric flux, as thermodynamics alone is not Hϩ H sufficient to calculate the values of the L coefficients. In Ϫ ij 2Ϫ SiO2 order to deal with this problem, it is necessary to extensively SiO3 SiO2 3 investigate the influence that electric charges on the surfaces ϩ ϩ H H have on the behaviour of fluids in contact with them, as 2Ϫ 2Ϫ SiO3 SiO3 illustrated below. 2Ϫ ϩ Hϩ Hϩ SiO3 H Hϩ ϩ Hϩ H 3.3.2 Formation and structure of the electrical double layer B Electrokinetic phenomena arise from the polarization Fig. 2. Formation of an electric double layer on a silica surface: process that takes place at the contact surface between a A, plane surface; B, spherical surface. 198 ENCYCLOPAEDIA OF HYDROCARBONS ELECTROKINETIC PHENOMENA iodide particles suspended in a solution of potassium iodide, infinite distance from the surface, the solution itself must be the molecules of which are adsorbed on the surface. electrically neutral, there is The study of the characteristics of electrical double 0 = [8] ∑CZii 0 layers was conducted by various authors who investigated i this problem at different levels. The first and most and it is possible to derive − χ significant studies, credited to G. Gouy and D.L. Chapman, [9] yy()z = 0e z date back to the beginning of the Twentieth century. These two authors described the surface as an infinite surface on where y0 is the value of the potential at the surface. which a continuous electric charge is distributed in contact Parameter c is expressed by with a solution containing point-like ions having opposite 8πe2 charges. At an infinite distance from the surface, the [10] χ 2 = ∑ CZ02 εkT ii electrical potential identifies with that of the solution, B i whereas when close to the surface, the potential gradually Therefore, the potential decreases exponentially; the 1/c varies until it assumes the values corresponding to the term has the dimensions of a length and represents the width surface itself. In this zone, two regions can be identified. where the surface double layer is basically located. One region includes the ions adsorbed on the surface and the By applying [5] and using the Debye-Hückel other, called the diffuse region, encompasses the ions present approximation, the following expression for the charge in the solution, whose distribution is determined by the density as a function of the coordinate z is obtained: conflict between electrostatic interactions to which they are 2 ε d y ε − χ subjected as well as random thermal movements. In general, [11] r =− =− χ 20y e z π 2 π ion adsorption produces an electrostatic energy barrier that 44dz hinders particle coagulation with the formation of a An important parameter in this analysis is the surface precipitated phase which is more stable from a electric charge density, referring to the unit area s0. Using thermodynamic point of view. In conclusion, at every the previous equation, s0 is expressed by: interphase there is an electrical double layer present, ∞ ∞ ε d 2y originating from the asymmetry of the force field involved. [12] σ =−r()zdz =dz = 0 ∫ ∫ π 2 In order to describe the characteristics of the double 0 0 4 dz layer in quantitative terms, it is appropriate to refer to a ε dy εχy0 =− = plane surface by simulating the layer of adsorbed ions with a 4π dz 4π continuous charge distribution.
Load more

Recommended publications
  • Nonlinear Electrokinetic Phenomena
    Nonlinear electrokinetic phenomena Synonyms Induced-charge electro-osmosis (ICEO), induced-charge electrophoresis (ICEP), AC electro- osmosis (ACEO), electro-osmosis of the second kind, electrophoresis of the second kind, Stotz-Wien effect, nonlinear electrophoretic mobility. Definition Nonlinear electrokinetic phenomena are electrically driven fluid flows or particle motions, which depend nonlinearly on the applied voltage. The term is also used more specifically to refer to induced-charge electro-osmotic flow, driven by an electric field acting on diffuse charge induced near a polarizable surface. Chemical and Physical Principles Linear electrokinetic phenomena A fundamental electrokinetic phenomenon is the electro-osmotic flow of a liquid electrolyte (solution of positive and negative ions) past a charged surface in response to a tangential electric field. Electrophoresis is the related phenomenon of motion of a colloidal particle or molecule in a background electric field, propelled by electro-osmotic flow in the opposite direction. The basic physics is as follows: Electric fields cause positive and negative ions to migrate in opposite directions. Since each ion drags some of the surrounding fluid with it, any significant local charge imbalance yields an electrostatic stress on the fluid. Ions also exert forces on each other, which tend to neutralize the bulk solution, so electrostatic stresses are greatest in the electrical double layers, where diffuse charge exists to screens surface charge. The width of the diffuse part of the double layer (or “diffuse layer”) is the Debye screening length (λ ~ 1-100 nm in water), which is much smaller than typical length scales in microfluidics and colloids. Such a “thin double layer” resembles a capacitor skin on the surface.
    [Show full text]
  • Electrokinetic Soil Processing in Waste Remediation and Treatment: Synthesis of Available Data
    TRANSPORTATION RESEARCH RECORD 1312 153 Electrokinetic Soil Processing in Waste Remediation and Treatment: Synthesis of Available Data YALCIN B. AcAR AND JIHAD HAMED Electrokinetic soil processing is an innovative in situ technique cantly affect the flow, the flow efficiency, and the extent of to remove contaminants from soils and groundwater. The process ion migration and removal in electrokinetic soil processing. is an alternative to conventional processes, with significant eco­ nomic and technical advantages. This paper provides a compre­ hensive review of the literature on electrokinetic soil processing. ELECTROKINETIC PHENOMENA IN SOILS The fundamentals of electrokinetic phenomena in soils and their potential use in waste management are presented. A synthesis of Coupling between electrical, chemical, and hydraulic gra­ available data on the technique is presented. Engineering impli­ dients is responsible for different types of electrokinetic phe­ cations regarding the current-voltage regime, duration energy nomena in soils. These phenomena include electroosmosis, requirements, and soil contaminant characteristics are provided. This review indicates that the process can be used efficiently to electrophoresis, streaming potential, and sedimentation po­ remove ions from saturated soil deposits. tential, as shown in Figure 1. Electroosmosis and electropho­ resis are the movement of water and particles, respectively, caused by application of a small direct current. Streaming The need to remove contaminants from soil and groundwater, potential and sedimentation potential are the generation of a the high cost of current remediation techniques ($50 to $1,500 current by the movement of water under hydraulic potential per cubic yard of soil), and limited resources lead to an ev­ and movement of particles under gravitational forces, re­ erlasting strife to find new, innovative, and cost-effective in spectively.
    [Show full text]
  • Induced-Charge Electrokinetic Phenomena
    Microfluid Nanofluid (2010) 9:593–611 DOI 10.1007/s10404-010-0607-2 REVIEW Induced-charge electrokinetic phenomena Yasaman Daghighi • Dongqing Li Received: 15 January 2010 / Accepted: 18 March 2010 / Published online: 7 April 2010 Ó Springer-Verlag 2010 Abstract The induced-charge electrokinetic (ICEK) with the surface charge or its ionic screening clouds (Sa- phenomena are relatively new area of research in micro- ville 1977; Anderson 1989). Typical electrokinetic phe- fluidics and nanofluidics. Different from the traditional nomena include: (i) electro-osmosis, liquid flow generated electrokinetic phenomena which are based on the interac- by an applied electric field force acting on the ionic charge tions between applied electric field and the electrostatic cloud near a solid surface; (ii) electrophoresis, the motion charge, the ICEK phenomena result from the interaction of of a charged particle in a liquid under an applied electric the applied electric field and the induced charge on po- field. larisable surfaces. Because of the different underline The ‘classical’ electrokinetics (EK) was first developed physics, ICEK phenomena have many unique characteris- in colloid sciences and surface chemistry (Hunter 2001; tics that may lead to new applications in microfluidics and Lyklema 1995; Anderson 1989) and has entered the mi- nanofluidics. In this paper, we review the major advance- crofluidics area over the past 10–15 years (Li 2004; Li ment of research in the field of ICEK phenomena, discuss 2008). Most studies of EK have assumed linear response to the applications and the limitations, and suggest some the applied electric field, and fixed static surface charge (Li future research directions.
    [Show full text]
  • Streaming Potential Analysis
    ABSTRACT WANG, YUN. Colloidal Behavior of Polyampholytes. (Under the direction of Dr. M. A. Hubbe). Polyampholytes are polymers that have both positively and negatively charged groups in the same chain. In recent years polyampholytes have started to be used in papermaking applications, as well as in sludge treatment processes. Benefits, in the case of papermaking, have included increased dry-strength and faster removal of water. But the molecular mechanisms by which such benefits are achieved have not been fully understood. This thesis project focused on effects related to polyampholyte charge density. A series of polyampholytes with a fixed charge ratio but different charge density was used for the experiments. Analysis methods included pH titrations, streaming current titrations, and adsorption isotherms. From pH titrations the charge density of cationic and anionic groups under different pH were calculated. From streaming current tests the net apparent charge density under different pH was calculated. And from adsorption tests it was found that the highest adsorbed amounts were achieved in certain cases corresponding to the highest content of ionic groups on the polyampholytes. Adsorption depended strongly on pH. Substantial differences were observed when comparing results obtained with polyampholyte samples versus ordinary polyelectrolyte samples with same charge density of cationic or anionic groups. Colloidal Behavior of Polyampholytes by YUN WANG A thesis submitted to the Graduate Faculty of North Carolina State University in partial fulfillment of the requirements for the Degree of Master of Science PULP AND PAPER SCIENCE Raleigh 2006 APPROVED BY: ________________________ _________________________ _________________________ Chair of Advisory Committee BIOGRAPHY The author was born on November 10, 1981 in Changzhou, Jiangsu province, People’s Republic of China.
    [Show full text]
  • On the Effect of Hydrodynamic Slip on the Polarization of a Nonconducting Spherical Particle in an Alternating Electric Field
    Mechanical Engineering Faculty Publications Mechanical Engineering 2010 On the Effect of Hydrodynamic Slip on the Polarization of a Nonconducting Spherical Particle in an Alternating Electric Field Hui Zhao University of Nevada, Las Vegas, [email protected] Follow this and additional works at: https://digitalscholarship.unlv.edu/me_fac_articles Part of the Electrical and Computer Engineering Commons, Mechanical Engineering Commons, and the Nanoscience and Nanotechnology Commons Repository Citation Zhao, H. (2010). On the Effect of Hydrodynamic Slip on the Polarization of a Nonconducting Spherical Particle in an Alternating Electric Field. Physics of Fluids, 22(7), 1-15. https://digitalscholarship.unlv.edu/me_fac_articles/557 This Article is protected by copyright and/or related rights. It has been brought to you by Digital Scholarship@UNLV with permission from the rights-holder(s). You are free to use this Article in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you need to obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Article has been accepted for inclusion in Mechanical Engineering Faculty Publications by an authorized administrator of Digital Scholarship@UNLV. For more information, please contact [email protected]. On the effect of hydrodynamic slip on the polarization of a nonconducting spherical particle in an alternating electric field Hui Zhao Citation: Phys. Fluids 22, 072004 (2010); doi: 10.1063/1.3464159 View online: http://dx.doi.org/10.1063/1.3464159 View Table of Contents: http://pof.aip.org/resource/1/PHFLE6/v22/i7 Published by the AIP Publishing LLC.
    [Show full text]
  • Arxiv:1907.04278V1 [Cond-Mat.Soft] 9 Jul 2019 As Schematically Shown in Fig
    Nonlinear Electrophoresis of Highly Charged Nonpolarizable Particles Soichiro Tottori, Karolis Misiunas, and Ulrich F. Keyser∗ Cavendish Laboratory, Department of Physics, University of Cambridge, JJ Thomson Avenue, Cambridge, CB3 0HE, United Kingdom Douwe Jan Bonthuis Institute of Theoretical and Computational Physics, Graz University of Technology, 8010 Graz, Austria (Dated: July 10, 2019) Nonlinear field dependence of electrophoresis in high fields has been investigated theoretically, yet experimental studies have failed to reach consensus on the effect. In this work, we present a systematic study on the nonlinear electrophoresis of highly charged submicron particles in applied electric fields of up to several kV/cm. First, the particles are characterized in the low-field regime at different salt concentrations and the surface charge density is estimated. Subsequently, we use microfluidic channels and video tracking to systematically characterize the nonlinear response over a range of field strengths. Using velocity measurements on the single particle level, we prove that nonlinear effects are present at electric fields and surface charge densities that are accessible in practical conditions. Finally, we show that nonlinear behavior leads to unexpected particle trapping in channels. Electrophoresis has been widely used for sensing, filtra- trokinetics found for polarizable particles [20], is not well tion, manipulation, and the separation of molecules and understood for intermediate to large κa in contrast to the particles, particularly recently using micro- and nanoflu- case of small κa in nonpolar electrolytes [21–26]. The- idic devices [1–4]. On these length scales, the applied oretical analyses have predicted that the electrophoretic electric field may reach kV/cm because the confinement velocity becomes nonlinear to the applied field at a mod- ∼ focuses the electric field, even with a moderate applied erate to high field β = aE/φth & 1 [14, 27–29].
    [Show full text]
  • Decontamination of Soil Using Electro-Osmosis. Jihad Tawfiq Ah Med Louisiana State University and Agricultural & Mechanical College
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1990 Decontamination of Soil Using Electro-Osmosis. Jihad Tawfiq aH med Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Hamed, Jihad Tawfiq, "Decontamination of Soil Using Electro-Osmosis." (1990). LSU Historical Dissertations and Theses. 5054. https://digitalcommons.lsu.edu/gradschool_disstheses/5054 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand corner and continuing from left to right in equal sections with small overlaps.
    [Show full text]
  • Numerical and Analytical Studies of the Electrical Conductivity of a Concentrated Colloidal Suspension
    J. Phys. Chem. B 2006, 110, 6179-6189 6179 Numerical and Analytical Studies of the Electrical Conductivity of a Concentrated Colloidal Suspension Juan Cuquejo,† Marı´a L. Jime´nez,‡ AÄ ngel V. Delgado,‡ Francisco J. Arroyo,§ and Fe´lix Carrique*,† Departamento de Fı´sica Aplicada I, Facultad de Ciencias, UniVersidad de Ma´laga, 29071 Ma´laga, Spain, Departamento de Fı´sica Aplicada, Facultad de Ciencias, UniVersidad de Granada, 18071 Granada, Spain, and Departamento de Fı´sica, Facultad de Ciencias Experimentales, UniVersidad de Jae´n, 23071 Jae´n, Spain ReceiVed: December 2, 2005; In Final Form: January 31, 2006 In the past few years, different models and analytical approximations have been developed facing the problem of the electrical conductivity of a concentrated colloidal suspension, according to the cell-model concept. Most of them make use of the Kuwabara cell model to account for hydrodynamic particle-particle interactions, but they differ in the choice of electrostatic boundary conditions at the outer surface of the cell. Most analytical and numerical studies have been developed using two different sets of boundary conditions of the Neumann or Dirichlet type for the electrical potential, ionic concentrations or electrochemical potentials at that outer surface. In this contribution, we study and compare numerical conductivity predictions with results obtained using different analytical formulas valid for arbitrary zeta potentials and thin double layers for each of the two common sets of boundary conditions referred to above. The conductivity will be analyzed as a function of particle volume fraction, φ, zeta potential, ú, and electrokinetic radius, κa (κ-1 is the double layer thickness, and a is the radius of the particle).
    [Show full text]
  • Influence of Surface Conductivity on the Apparent Zeta Potential of Calcite
    Influence of surface conductivity on the apparent zeta potential of calcite Shuai Li, Philippe Leroy, Frank Heberling, Nicolas Devau, Damien Jougnot, Christophe Chiaberge To cite this version: Shuai Li, Philippe Leroy, Frank Heberling, Nicolas Devau, Damien Jougnot, et al.. Influence of surface conductivity on the apparent zeta potential of calcite. Journal of Colloid and Interface Science, Elsevier, 2016, 468, pp.262-275. 10.1016/j.jcis.2016.01.075. hal-01282487 HAL Id: hal-01282487 https://hal.archives-ouvertes.fr/hal-01282487 Submitted on 3 Mar 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Influence of surface conductivity on the apparent zeta potential of calcite Shuai Li1, Philippe Leroy1*, Frank Heberling2, Nicolas Devau1, Damien Jougnot3, Christophe Chiaberge1 1 BRGM, French geological survey, Orléans, France. 2 Institute for Nuclear Waste Disposal, Karlsruhe Institute of Technology, Karlsruhe, Germany. 3 Sorbonne Universités, UPMC Univ Paris 06, CNRS, EPHE, UMR 7619 METIS, Paris, France. *Corresponding author and mailing address: Philippe Leroy BRGM 3 Avenue Claude Guillemin 45060 Orléans Cedex 2, France E-mail: [email protected] Tel: +33 (0)2 38 64 39 73 Fax: +33 (0)2 38 64 37 19 This paper has been accepted for publication in Journal of Colloid and Interface Science: S.
    [Show full text]
  • 5. Chemical Physics of Colloid Systems and Interfaces
    Published as Chapter 5 in "Handbook of Surface and Colloid Chemistry" Second Expanded and Updated Edition; K. S. Birdi, Ed.; CRC Press, New York, 2002. 5. CHEMICAL PHYSICS OF COLLOID SYSTEMS AND INTERFACES Authors: Peter A. Kralchevsky, Krassimir D. Danov, and Nikolai D. Denkov Laboratory of Chemical Physics and Engineering, Faculty of Chemistry, University of Sofia, Sofia 1164, Bulgaria CONTENTS 5.7. MECHANISMS OF ANTIFOAMING……………………………………………………..166 5.7.1 Location of Antifoam Action – Fast and Slow Antifoams 5.7.2 Bridging-Stretching Mechanism 5.7.3 Role of the Entry Barrier 5.7.3.1 Film Trapping Technique 5.7.3.2 Critical Entry Pressure for Foam Film Rupture 5.7.3.3 Optimal Hydrophobicity of Solid Particles 5.7.3.4 Role of the Pre-spread Oil Layer 5.7.4 Mechanisms of Compound Exhaustion and Reactivation 5.8. ELECTROKINETIC PHENOMENA IN COLLOIDS……………………………………...183 5.8.1 Potential Distribution at a Planar Interface and around a Sphere 5.8.2 Electroosmosis 5.8.3 Streaming Potential 5.8.4 Electrophoresis 5.8.5 Sedimentation Potential 5.8.6 Electrokinetic Phenomena and Onzager Reciprocal Relations 5.8.7 Electric Conductivity and Dielectric Response of Dispersions 5.8.7.1 Electric Conductivity 5.8.7.2 Dispersions in Alternating Electrical Field 5.8.8 Anomalous Surface Conductance and Data Interpretation 5.8.9 Electrokinetic Properties of Air-Water and Oil-Water Interfaces 5.9. OPTICAL PROPERTIES OF DISPERSIONS AND MICELLAR SOLUTIONS………….207 5.9.1 Static Light Scattering 5.9.1.1 Rayleigh Scattering 5.9.1.2 Rayleigh-Debye-Gans Theory 5.9.1.3
    [Show full text]
  • Recent Advances in the Modelling and Simulation
    Recent advances in the modelling and simulation of electrokinetic effects: bridging the gap between atomistic and macroscopic descriptions Ignacio Pagonabarraga, Benjamin Rotenberg, Daan Frenkel To cite this version: Ignacio Pagonabarraga, Benjamin Rotenberg, Daan Frenkel. Recent advances in the modelling and simulation of electrokinetic effects: bridging the gap between atomistic and macroscopic de- scriptions. Physical Chemistry Chemical Physics, Royal Society of Chemistry, 2010, 12, pp.9566. 10.1039/C004012F. hal-00531720 HAL Id: hal-00531720 https://hal.archives-ouvertes.fr/hal-00531720 Submitted on 8 Nov 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Recent advances in the modelling and simulation of electrokinetic effects: bridging the gap between atomistic and macroscopic descriptions I. Pagonabarraga∗ B. Rotenberg† D. Frenkel‡ May 27, 2010 Abstract Electrokinetic phenomena are of great practical importance in fields as diverse as micro-fluidics, colloid science and oil exploration. However, the quantitative prediction of electrokinetic effects was until recently limited to relatively simple geometries that allowed the use of analytical theories. In the past decade, there has been a rapid development in the use of numerical methods that can be used to model electrokinetic phenomena in complex geometries or, more generally, under conditions where the existing analytical approaches fail.
    [Show full text]
  • Influence of Surface Conductivity on the Apparent Zeta Potential of Calcite
    Influence of surface conductivity on the apparent zeta potential of calcite Shuai Li1, Philippe Leroy1*, Frank Heberling2, Nicolas Devau1, Damien Jougnot3, Christophe Chiaberge1 1 BRGM, French geological survey, Orléans, France. 2 Institute for Nuclear Waste Disposal, Karlsruhe Institute of Technology, Karlsruhe, Germany. 3 Sorbonne Universités, UPMC Univ Paris 06, CNRS, EPHE, UMR 7619 METIS, Paris, France. *Corresponding author and mailing address: Philippe Leroy BRGM 3 Avenue Claude Guillemin 45060 Orléans Cedex 2, France E-mail: [email protected] Tel: +33 (0)2 38 64 39 73 Fax: +33 (0)2 38 64 37 19 This paper has been accepted for publication in Journal of Colloid and Interface Science: S. Li, P. Leroy, F. Heberling, N. Devau, D. Jougnot, C. Chiaberge (2015) Influence of surface conductivity on the apparent zeta potential of calcite, Journal of Colloid and Interface Science, 468, 262-275, doi:10.1016/j.jcis.2016.01.075. 1 Abstract Zeta potential is a physicochemical parameter of particular importance in describing the surface electrical properties of charged porous media. However, the zeta potential of calcite is still poorly known because of the difficulty to interpret streaming potential experiments. The Helmholtz- Smoluchowski (HS) equation is widely used to estimate the apparent zeta potential from these experiments. However, this equation neglects the influence of surface conductivity on streaming potential. We present streaming potential and electrical conductivity measurements on a calcite powder in contact with an aqueous NaCl electrolyte. Our streaming potential model corrects the apparent zeta potential of calcite by accounting for the influence of surface conductivity and flow regime.
    [Show full text]