Digital Signal Processing with the EFM32
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
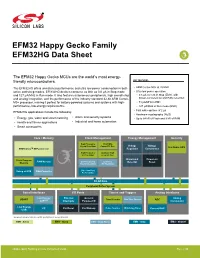
EFM32 Happy Gecko Family EFM32HG Data Sheet
EFM32 Happy Gecko Family EFM32HG Data Sheet The EFM32 Happy Gecko MCUs are the world’s most energy- friendly microcontrollers. KEY FEATURES The EFM32HG offers unmatched performance and ultra low power consumption in both • ARM Cortex-M0+ at 25 MHz active and sleep modes. EFM32HG devices consume as little as 0.6 μA in Stop mode • Ultra low power operation and 127 μA/MHz in Run mode. It also features autonomous peripherals, high overall chip • 0.6 μA current in Stop (EM3), with and analog integration, and the performance of the industry standard 32-bit ARM Cortex- brown-out detection and RAM retention M0+ processor, making it perfect for battery-powered systems and systems with high- • 51 μA/MHz in EM1 performance, low-energy requirements. • 127 μA/MHz in Run mode (EM0) • Fast wake-up time of 2 µs EFM32HG applications include the following: • Hardware cryptography (AES) • Energy, gas, water and smart metering • Alarm and security systems • Up to 64 kB of Flash and 8 kB of RAM • Health and fitness applications • Industrial and home automation • Smart accessories Core / Memory Clock Management Energy Management Security High Frequency 48/24 MHz Voltage Voltage Crystal Oscillator Comm. RC Osc. Hardware AES ARM CortexTM M0+ processor Regulator Comparator High Frequency Auxiliary High RC Oscillator Freq. RC Osc. Brown-out Power-on Flash Program RAM Memory Low Frequency Low Freq. Detector Reset Memory Crystal Oscillator RC Oscillator Debug w/ MTB DMA Controller Ultra Low Freq. RC Oscillator 32-bit bus Peripheral Reflex System Serial Interfaces I/O Ports Timers and Triggers Analog Interfaces Low Energy External General Analog USART Timer/Counter Real Time Counter ADC UARTTM Interrupts Purpose I/O Comparator Low Energy I2C Pin Reset Pin Wakeup Pulse Counter Watchdog Timer Current DAC USB Lowest power mode with peripheral operational: EM0 - Active EM1 - Sleep EM2 – Deep Sleep EM3 - Stop EM4 - Shutoff silabs.com | Building a more connected world. -

Silicon Labs to Acquire Energy Micro, a Leader in Low Power ARM Cortex-Based Microcontrollers and Radios
June 7, 2013 Silicon Labs to Acquire Energy Micro, a Leader in Low Power ARM Cortex-Based Microcontrollers and Radios Companies' Combined Portfolios Enable the Internet of Things, Smart Energy and Portable Electronics AUSTIN, Texas & OSLO, Norway--(BUSINESS WIRE)-- Silicon Labs (Nasdaq: SLAB), a leader in high-performance, analog- intensive, mixed-signal ICs, today announced that it has signed a definitive agreement to acquire Energy Micro AS. Based in Oslo, Norway, the late-stage privately held company offers the industry's most power-efficient portfolio of 32-bit microcontrollers (MCUs) and is developing multi-protocol wireless RF solutions based on the industry-leading ARM® Cortex-M architecture. Energy Micro's energy-friendly MCU and radio solutions are designed to enable a broad range of power-sensitive applications for the Internet of Things (IoT), smart energy, home automation, security and portable electronics markets. This strategic acquisition accelerates Silicon Labs' growth opportunities and positions the company as the foremost innovator in energy-friendly embedded solutions. The growth of the IoT market, coupled with continued deployment of smart grid and smart energy infrastructure, is driving strong demand for energy-efficient processing and wireless connectivity technology to enable connected devices in which low-power capabilities are increasingly important. Industry experts predict that the number of connected devices for the IoT will top 15 billion nodes by 2015 and reach 50 billion nodes by 2020. Energy Micro's portfolio complements Silicon Labs' 32-bit Precision32™ MCU, Ember® ZigBee® and sub-GHz wireless products and targets a growing embedded market. The acquisition greatly expands Silicon Labs' MCU portfolio, adding nearly 250 ARM- based EFM32 Gecko MCU products ranging from extreme-low-power, small-footprint MCUs based on the ARM Cortex-M0+ core to higher-performance, energy-friendly MCUs powered by the Cortex-M4 core capable of DSP and floating-point operations. -

Embedded Market Study, 2013
2013 EMBEDDED MARKET STUDY Essential to Engineers DATASHEETS.COM | DESIGNCON | DESIGN EAST & DESIGN WEST | EBN | EDN | EE TIMES | EMBEDDED | PLANET ANALOG | TECHONLINE | TEST & MEASUREMENT WORLD 2013 Embedded Market Study 2 UBM Tech Electronics’ Brands Unparalleled Reach & Experience UBM Tech Electronics is the media and marketing services solution for the design engineering and electronics industry. Our audience of over 2,358,928 (as of March 5, 2013) are the executives and engineers worldwide who design, develop, and commercialize technology. We provide them with the essentials they need to succeed: news and analysis, design and technology, product data, education, and fun. Copyright © 2013 by UBM. All rights reserved. 2013 Embedded Market Study 5 Purpose and Methodology • Purpose: To profile the findings of the 2013 results of EE Times Group annual comprehensive survey of the embedded systems markets worldwide. Findings include types of technology used, all aspects of the embedded development process, tools used, work environment, applications, methods and processes, operating systems used, reasons for using and not using chips and technology, and brands and chips currently used by or being considered by embedded developers. Many questions in this survey have been trended over two to five years. • Methodology: A web-based online survey instrument based on the previous year’s survey was developed and implemented by independent research company Wilson Research Group from January 18, 2013 to February 13, 2013 by email invitation • Sample: E-mail invitations were sent to subscribers to UBM/EE Times Group Embedded Brands with one reminder invitation. Each invitation included a link to the survey. • Returns: 2,098 valid respondents for an overall confidence of 95% +/- 2.13%. -

SEGGER Microcontroller Embedded Software Suite to Support Energy Micro’S Cortex-M3 Gecko Microcontrollers
Company news Reference: EM0063 SEGGER Microcontroller embedded software suite to support Energy Micro’s Cortex-M3 Gecko microcontrollers Hilden, Germany and Oslo, Norway, December 7 2011 – SEGGER Microcontroller, a leading provider of software solutions for embedded applications, and Energy Micro, the energy friendly microcontroller and radio company, have announced that SEGGER’s high-performance embedded middleware suite now supports Energy Micro’s range of ultra low energy ARM® Cortex™-M3 based EFM32 Gecko microcontrollers. The comprehensive feature-rich and high-performance software suite from SEGGER delivers an easy-to-use environment for embedded systems development, offering exceptionally low memory requirements, which minimizes Bill-of-Materials costs and enables significantly reduced power consumption overall. The middleware’s high performance also enables lower clock speed to further reduce system power consumption. Specific tools from SEGGER supporting the Energy Micro EFM32 Gecko MCUs include: the real-time operating system "embOS" which offers multitasking with minimal resources and true zero interrupt latency; the embedded file system "emFile" which is optimized for minimum RAM memory consumption supporting SD-card, NAND and NOR flash memory with wear levelling; and the efficient "emWin" user interface, an LCD controller-independent graphical user interface (GUI) for applications requiring a graphics display. The high-quality graphical software, which runs with any display or any MCU, delivers flicker-free animation, optimized drawing routines with optional anti-aliasing, and a GUI builder for Window Objects (Widgets). Thanks to the long-term partnership between the two companies, all Energy Micro development and starter kits are supplied with SEGGER’s J-Link emulation technology, and the latest Leopard and Giant Gecko development kits also include SEGGER´s advanced J-Trace. -

QSG166: WF200 Wi-Fi Development Kit Quick Start Guide
QSG166: WF200 Wi-Fi Development Kit Quick Start Guide The WF200 Wi-Fi Development Kit is an excellent way to get star- ted with WF200 Wi-Fi transceiver IC to achieve performance eval- KEY CONTENTS uation and software development. • Expansion Board with the WF200 Wi-Fi transceiver IC onboard. It supports various hardware and software use cases, as described below. • Direct connection to Silicon Labs EFM32 and EFR32 hosts (20 pin EXP) Two versions of devkits are available: • Direct connection to Raspberry Pi for the • SLEXP8022A contains WF200 development board (BRD8022A), that can be connec- Linux use case ted to Silicon Labs EFM32 or EFR32 Starter kits or to a Raspberry Pi for the Linux • Support of 3rd party MCUs case. It also contains a micro-SD card allowing fast startup with a Raspberry Pi. • Selectable SPI or SDIO host interface • SLEXP8022B is a superset of SLEXP8022A with a Raspberry Pi 2 model V1.2 inclu- ded. This document described the first steps to get a Wi-Fi connection for the Linux case (Raspberry Pi), Silicon Labs MCUs, as well as a case with a 3rd party MCU. Note: Refer to UG379 for more details about the board. silabs.com | Building a more connected world. Rev. 0.2 Table of Contents 1. Getting Started with Raspberry Pi and Linux ...................3 1.1 Requirements ..............................3 1.1.1 Hardware ..............................3 1.1.2 Software ..............................3 1.2 Hardware Setup .............................3 1.3 SSH Connection .............................4 1.4 Wi-Fi Demos...............................4 1.4.1 Station Demo .............................4 1.4.2 Access Point Demo ...........................5 1.5 Update SD Card .............................5 1.6 Software Repositories ...........................5 2. -

Developing Rust on Bare-Metal
RustyGecko - Developing Rust on Bare-Metal An experimental embedded software platform Håvard Wormdal Høiby Sondre Lefsaker Master of Science in Computer Science Submission date: June 2015 Supervisor: Magnus Lie Hetland, IDI Co-supervisor: Antonio Garcia Guirado, IDI Marius Grannæs, Silicon Labs Norwegian University of Science and Technology Department of Computer and Information Science Preface This report is submitted to the Norwegian University of Science and Technology in fulfillment of the requirements for master thesis. This work has been performed at the Department of Computer and Information Science, NTNU, with Prof. Magnus Lie Hetland as the supervisor, Antonio Garcia Guirado (ARM), and Marius Grannæs (Silicon Labs) as co-supervisors. The initial problem description was our own proposal and further developed in co-operation with our supervisors. Acknowledgements Thanks to Magnus Lie Hetland, Antonio Garcia Guirado, and Marius Grannæs for directions and guidance on technical issues and this report. Thanks to Silicon Labs for providing us with development platforms for us to develop and test our implementation on. Thanks to Antonio Garcia Guirado for the implementation of the CircleGame application for us to port to Rust and use in our benchmarks. Thanks to Itera w/Tommy Ryen for office space. A special thanks to Leslie Ho and Siri Aagedal for all the support and for proofreading the thesis. Sondre Lefsaker and H˚avard Wormdal Høiby 2015-06-14 i Project Description The Rust programming language is a new system language developed by Mozilla. With the language being statically compiled and built on the LLVM compiler infras- tructure, and because of features like low-level control and zero-cost abstractions, the language is a candidate for use in bare-metal systems. -

UG416: EFM32 Gecko Starter Kit User's Guide
UG416: EFM32G Gecko Starter Kit User's Guide The EFM32-G8XX-STK Starter Kit is an excellent starting point to become familiar with the EFM32G™ Gecko Microcontroller. TARGET DEVICE The Starter Kit contains sensors and peripherals demonstrating some of the Gecko's • EFM32G Gecko Microcontroller (EFM32G890F128G-E-BGA112R) many capabilities. The kit provides all necessary tools for developing an EFM32G Gecko application. • CPU: 32-bit ARM® Cortex-M3 • Memory: 128 kB flash and 16 kB RAM KIT FEATURES • USB connectivity • Advanced Energy Monitor (AEM) • SEGGER J-Link on-board debugger • Debug Multiplexer supporting external hardware as well as on-board MCU • User LEDs / Pushbuttons • 160 segment LCD • 4-segment capacitive touch slider and touch button • 20-pin 2.54 mm header for expansion boards • Breakout pads for direct access to I/O pins • Power sources include USB and CR2032 coin cell battery. SOFTWARE SUPPORT • Simplicity Studio™ • IAR Embedded Workbench silabs.com | Building a more connected world. Rev. 2.00 Table of Contents 1. Introduction ................................3 1.1 Description ...............................3 1.2 Features ................................3 1.3 Getting Started ..............................3 2. Kit Block Diagram .............................4 3. Kit Hardware Layout ............................5 4. Connectors ................................6 4.1 Breakout Pads ..............................6 4.2 Expansion Header .............................8 4.3 Debug Connector (DBG) ..........................10 4.4 Simplicity Connector ............................11 5. Power Supply and Reset ..........................12 5.1 MCU Power Selection ...........................12 5.2 Board Controller Power ...........................12 5.3 EFM32G Reset ..............................13 6. Peripherals ...............................14 6.1 Push Buttons and LEDs ...........................14 6.2 LCD .................................15 6.3 Capacitive Touch Slider ...........................15 6.4 Virtual COM Port .............................16 7. -

Portable ISP Programmer for Field-Service and Production Applications
Supporting FLASH microcontrollers Portable ISP Programmer for Field-Service and Production applications ARM Devices Supported... The EPSILON5-MK4(ARM) programmer being used in Standalone Mode STM32 F1 STM32 F2 STM32 F4 STM32 L1 Mainstream MCUs High-performance MCUs High-performance MCUs Ultra-low-power MCUs The EPSILON5-MK4(ARM) is a high-speed portable programmer with DSP and FPU designed for field-service and production In-System Programming Support coming soon for... (ISP) applications. It supports programming of many popular ARM FLASH microcontroller devices via the ARM JTAG Debug Interface. The programmer is capable of operating in ‘Standalone Mode’ (without PC) ZERO TINY GECKO Cortex-M0+ Zero Gecko Cortex-M3 Tiny Gecko Cortex-M3 Gecko Cortex® - M0+ Cortex® - M3 Cortex® - M3 allowing an operator to program a single project only. For field / production Microcontroller Microcontroller Microcontroller LEOPARD GIANT WONDER Cortex-M3 Leopard Gecko Cortex-M4 Giant Gecko Cortex-M3 Wonder Gecko Cortex® - M3 Cortex® - M4 Cortex® - M3 applications the unit is designed to operate in ‘Standalone Mode’. A Microcontroller Microcontroller Microcontroller ‘Standalone Programming Project’ can be recalled from the on-board non-volatile FLASH memory and programmed into a Target System by pressing a single key. All the popular ARM ISP connection headers are catered for. ● STM32 F0 STM32 F3 STM32 W Portable In-System (ISP) Programmer Entry level MCUs Mixed-signal MCUs Wireless MCUs, ● Ideal for Field-service or low-volume Production programming with -

Etrx35x ZIGBEE MODULES PRODUCT MANUAL
Telegesis™ TG-ETRX35X-PM-010-110 ETRX351 and ETRX357 Product Manual 1.10 Telegesis™ is a trademark of Silicon Laboratories Inc. ETRX35x ZIGBEE MODULES PRODUCT MANUAL ©2015 Silicon Labs ETRX35x Product Manual ETRX351 and ETRX357 Table of Contents 1 INTRODUCTION ................................................................................................................. 5 1.1 Hardware Description ....................................................................................................... 5 2 PRODUCT APPROVALS ................................................................................................... 6 2.1 FCC Approvals ................................................................................................................. 6 FCC Labelling Requirements ........................................................................................... 7 2.2 IC (Industry Canada) Approvals ....................................................................................... 7 2.3 European Certification (ETSI)........................................................................................... 8 2.4 ICASA Approvals ............................................................................................................. 8 2.5 Australia and New Zealand (C-Tick) ................................................................................. 8 2.6 Brazil ................................................................................................................................ 9 2.7 Declarations of Conformity -

Note on How to Install Openblp Bootloader For
Note on how to install OpenBLP bootloader for OLIMEX's EM32G880F128-STK STM32-H103 STM32-P103 LPC-L2294 A friend of Olimex provides and supports a pretty nice bootloader released under GNU GPL altogether with a neat and tidy Wiki. The main page of this project is: http://feaser.com/openblt/doku.php There is a lot of info about the features of the project but I want to specifically point how well everything is organized and documented. If you look the examples page there are a number of Olimex boards also supported: http://feaser.com/openblt/doku.php?id=manual:demos Further more, there are very good guides on making everything work together using different ways of downloading the code on those boards. Having bootloader on EM32G880F128-STK is real treat, because that way a person doesn't need an expensive SWD debugger for the board. That being said the installation of the OpenBLT on the other boards doesn't differ much from the one I will present. Below you will find the installation of OpenBLT on EM32G880F128-STK using OLIMEX ARM- USB-OCD combined with ARM-JTAG-SWD. The IDE I will be using is Rowley's Crossworks for ARM which supports our SWD interface out of the box. 1) First step is to install the Crossworks IDE and the driver for the ARM debugger. We also mount the SWD adapter between the debugger and the cable it is shipped with. 2) Open Crosswork IDE and make sure you right-click install the Energy Micro EFM32 support package. -

ESD March 2014
desigMarchn 2014 | Volume 4, Issue 3 www.electronicspecifier.com Could GFETs drive RF integration? News Advanced Power Development Tools All the news from Processes Semiconductors Embedded World 2014 The last piece of the Ultra-Thin is the New Let there be better LED puzzle Bulk light UNBEATABLE ON PRODUCTION ELECTRONICS Q Production ready packaging Q Great prices Q Enhanced product range now with greater depth Q Leading date and lot traceability Q FAST next day delivery CHALLENGE US TODAY SUPPORTING PRODUCTION WE ARE READY TO WIN YOUR NEXT ORDER Visit www.farnell.com/production 09:10 design Contents 06 News All the news from this year’s Embedded World 14 Markets & Trends 12 Smart Energy Systems The last piece of the puzzle 14 Could a new process for CMOS RF power match GaAs? Could GFETs drive RF integration? 18 The latest research around Graphene FETs Building better memories 20 Developments in Charge Trap engineering could challenge Flash 22 Ultra-Thin is the New Bulk 21 Smaller, faster, cheaper devices promised by a new SOI process Taking back the power 22 PMICs target the ultra-portable Raging trench warfare 26 While breakthroughs may be slowing, development continues Monitoring your health 29 Structural health monitoring on a big scale 29 Let there be better LED light 34 Thermal issues are key to LED efficiency It’s all in the timing 38 Manufacturers continue to deliver the tools needed by designers Try before you buy 42 Taking a look at the development kits launched at Embedded World The 3 flavours of Bluetooth 44 Making it simpler to get connected 44 Editor: Ad sales: Head Office: Copyright 2013 Electronic Specifier. -

Silicon Labs EFM32 Tiny Gecko TG11 Starter Kit User's Guide
UG303: EFM32 Tiny Gecko TG11 Starter Kit User's Guide The SLSTK3301A Starter Kit is an excellent starting point to get familiar with the EFM32™ Tiny Gecko TG11 Microcontroller. TARGET DEVICE The Starter Kit contains sensors and peripherals demonstrating some of the Tiny Gecko • EFM32 Tiny Gecko TG11 Microcontroller (EFM32TG11B520F128GM80) TG11's many capabilities. The kit provides all necessary tools for developing an EFM32 Tiny Gecko TG11 application. • CPU: 32-bit ARM® Cortex-M0+ • Memory: 128 kB flash and 32 kB RAM KIT FEATURES • USB connectivity • Advanced Energy Monitor • SEGGER J-Link on-board debugger • Debug Multiplexer supporting external hardware as well as on-board MCU • Silicon Labs Si7021 Relative Humidity and Temperature sensor • User LEDs / Pushbuttons • 8x28 Segment LCD • Inductive LC sensor • Silicon Labs Si7210 Hall-Effect Sensor • Capacitive Touch Slider • 20-pin 2.54 mm header for EXP boards • Breakout pads for direct access to I/O pins • Power sources include USB and CR2032 coin cell battery. SOFTWARE SUPPORT • Simplicity Studio™ • IAR Embedded Workbench silabs.com | Building a more connected world. Rev. 1.0 Table of Contents 1. Introduction ................................4 1.1 Description ...............................4 1.2 Features................................4 1.3 Getting Started .............................4 2. Kit Block Diagram .............................5 3. Kit Hardware Layout ............................6 4. Connectors ................................7 4.1 Breakout Pads .............................7