DOCSLIB.ORG

Heats-Of-Combustion and of Formation of the Normal Paraffin Hydrocarbons

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Heats-Of-Combustion and of Formation of the Normal Paraffin Hydrocarbons U.S. Department of Commerce National Bureau of Standards RESEARCH PAPER RP692 Part ofJournal of Research, of the Rational Bureau of Standards, vol 13, July 193^ HEATS OF COMBUSTION AND OF FORMATION OF THE NORMAL PARAFFIN HYDROCARBONS IN THE GAS- EOUS STATE, AND THE ENERGIES OF THEIR ATOMIC LINKAGES By Frederick D. Rossini abstract From the data recently obtained in this laboratory on the heats of combus- tion of methane, ethane, propane, normal butane, and normal pentane, reliable values are deduced for the heats of combustion of all the other normal paraffin hydrocarbons in the gaseous state. For normal C wH 2n+2 (gas), with n>5, the heat of combustion, at a temperature of 25 C and a constant total pressure of 1 atmosphere, in gaseous oxygen to form gaseous carbon dioxide and liquid water, is 60.40 + n(157.00±0.08) k — cali 5 per mole. (This unit of energy is a defined one and is derived from the fundamental international joule by means of the factor 1.00040/4.1850.) The following generalization is made: In any organic molecule containing a normal alkyl group of more than 5 carbon atoms, the addition of a CH 2 group to the normal alkyl group to form the next higher normal alkyl group results in an increase in the heat of combustion of the organic molecule in the gaseous state, at a temperature of 25 C and a constant total pressure of 1 atmosphere, of 157.00 ± 0.08 k -cali 5 per mole. From these and other data values are computed for the heats of formation, from hydrogen and /3-graphite and diamond, respectively, of all the normal paraffin hydrocarbons in the gaseous state at temperatures of 25 C and Kelvin. The energy of dissociation, at zero Kelvin, of a gaseous normal paraffin hydrocarbon, C nH 2n +2 , into gaseous carbon and hydrogen atoms, is shown to be a linear function of n above, but not linear below, n— 6. The deviations from linearity for the latter are in the direction of greater stability of the molecule and have the following values: Methane, 4.81 ±0.08; ethane, 1.59 ±0.14; pro- pane, 0.83 ±0.19; normal butane, 0.46 ±0.27; normal pentane, 0.13 ±0.37, k-cal per mole. It is shown that for the normal paraffin hydrocarbons, and for carbon and hydrogen atoms in the normal state, the energy evolved in the reaction C (gas) + 2H(gas) + C wH 2n+2 (gas)=C n+ iH 2n+ 4 (gas), for n>5, at Kelvin, is — AH%= (20.8 ±0.9) + Dco k-cali 5 per mole (Dco is the energy of dissociation of CO at Kelvin) ; and any assignment of values for Dco , for the energy of excitation of the carbon atom to the 5S state, and for the energies of the 1 C-C and 2 C-H bonds formed in the reaction must satisfy this relation. CONTENTS Page I. Introduction 22 II. Heats of combustion 23 III. Heats of formation from the elements 26 1. At 25 centigrade 26 2. At Kelvin = 29 IV. Change in heat content for the reaction nCO (gas) + (n+l)H 2 (gas) n/2 2 (gas) = C„H 2n+2 (gas) 30 V. Energies of the atomic linkages 30 VI. References 35 21 22 Journal oj Research of the National Bureau of Standards [vol. is I. INTRODUCTION In this paper the writer utilizes the data on the heats of combustion of methane, ethane, propane, normal butane, and normal pentane 1 recently obtained in this laboratory (1, 25) for the following pur- poses: First, to predict accurate values for the heats of combustion of the normal gaseous paraffin hydrocarbons containing more than 5 carbon atoms; second, to compute values for the heats of formation of all the normal paraffin hydrocarbons in the gaseous state; and third, to test the accuracy of the postulate of the constancy of the energies of the atomic linkages in these molecules. Because of the increasing industrial importance of vapor phase reactions involving the paraffin hydrocarbons, there is great need for values of the heats of formation of these substances in the gaseous state, for making calculations of the chemical equilibria involved. The heats of combustion of hydrocarbons have been of considerable interest to the physical chemist for many years. Speculation con- cerning the influence of structure and of the number of carbon atoms upon the energy content of hydrocarbon molecules began as early as 1869, when Hermann (2) utilized for this purpose the data on heats of combustion obtained by Favre and Silbermann (4) about 15 years earlier. From the results of his own measurements, reported in 1886 in the fourth volume of his monumental treatise on thermochemistry, Thomsen (3) showed that, in general, the addition of a CH2 group to any molecule in the gaseous state resulted in an increase in its heat of combustion of about 158 kilocalories per mole. And, in particular, Thomsen's values for methane, ethane, propane, isobutane, and tetramethylmethane showed constant successive differences in the heats of combustion, at constant pressure and a temperature of 18 C, of 158.34 ±0.20 kilocalories per mole. Except for the meager data of Berthelot and Matignon (5) on ethane and propane, and the isolated value of Koth and Machlett (6) on pentane, no data on the heats of combustion of the gaseous paraffin hydrocarbons above methane were reported during the half century following Thomsen's measurements. Thus it was only natural that Thomsen's data were used to substantiate the almost universally accepted postulate of the constancy of the energies of the C-C and C-H linkages in the saturated hydrocarbon molecules. Many calculations have been made in recent years concerning the postulate of the constancy of bond energies in the paraffin hydro- carbons. In his recent book on "The Covalent Link in Chemistry", published in 1933, Sidgwick (7) writes: " * * * and so the values of the heats of formation of the [atomic] links [in the paraffin hydro- carbons] should be independent of the number of atoms in the mole- cule, as in fact they are found to be." In particular, one may cite the recent, 1932, calculations of Pauling 2 (8) who showed that, using the values given by Kharasch (9) for the heats of combustion of methane, ethane, propane, butane, hexane, and heptane, the energies of formation from gaseous atoms calcu- lated on the assumption of constant energies for the C-H and C-C 1 Figures in parentheses here and throughout the text refer to the references at the end of this paper, p. 35. 2 The values given by Kharasch (9) for methane, ethane, propane, and butane are based on the calori- metric data of Thomsen (3). Rossini] Heats of Combustion and Formation 23 bonds were practically identical with the values computed from heats of combustion plus some auxiliary data. 3 The differences between the values calculated by the two methods were such as to be equiva- lent to errors of less than 0.1 percent in the heats of combustion, or about 0.2 kilocalorie per carbon atom. This agreement is quite ex- traordinary because it borders on the very limit of the calorimetric precision obtainable by Thomsen (3), and there must be superim- posed upon his calorimetric uncertainty errors due to the large cor- rections for impurities in the samples of hydrocarbons burned by him. This latter uncertainty is probably much greater than Thomsen's calorimetric error because his various samples had the following empirical formulas: Ethane, propane, C2 H6 . 54, C2 H6 . C 3H . 33; 7 991 ; isobutane, ; tetramethylmethane ; . C 4H 9 . 748 , C4H9 . 899 C5Hn.78 , C 5 Hn.64 Thomsen assumed that his last sample of pentane was, in mole per- cent, 78.5 CfiHw + 21.5 C4H8 . Because of these facts, it has seemed desirable that an accurate test be made of the postulate of the constancy of the energies of the atomic linkages in the simple paraffin hydrocarbon molecules, by discovering, if possible, any real deviation from linearity in the heats of combustion of the members of the series. With the data on heats of combustion recently obtained in this laboratory (1), it is now possible to submit the postulate to a more rigorous test. II. HEATS OF COMBUSTION According to prevailing ideas, the heats of combustion of the paraffin hydrocarbons in the gaseous state should show constant differences between successive members of the series. That is to say, the heat of combustion will be a linear function of the number of carbon atoms, Qc = A + Bn (1) where Qc is the heat of combustion of a gaseous normal paraffin hydro- carbon containing n carbon atoms, B is the constant increment per carbon atom or CH2 group, and A is a constant. This relation may be expressed also as (Qc-A)/n = B (2) The following are the data recently obtained in this laboratory (1) on the heats of combustion of the gases at a temperature of 25 C and 4 a constant total pressure of 1 atmosphere, in k-cali 5 per mole: Methane 212. 79±0. 07 Ethane 372. 81±0. 11 Propane 530. 57±0. 12 Normal butane 687. 94±0. 15 Normal pentane 845. 27±0. 21 Examination of these values shows that the successive differences are 160.02, 157.76, 157.37, and 157.33, respectively. These differences are quite significantly not constant, but are apparently approaching a 3 The nature of the calculation is such that the use of different values for the subsidiary data changes only the actual values of the C-H and C-C bond energies, not their constancy from one molecule to another.
Load more

Recommended publications
  • A Confinement Strategy to Prepare N-Doped Reduced Graphene Oxide
    Electronic Supplementary Material (ESI) for Nanoscale. This journal is © The Royal Society of Chemistry 2019 Supporting Information A confinement strategy to prepare N-doped reduced graphene oxide foams with desired monolithic structures for supercapacitors Daoqing Liu,a,b,# Qianwei Li, *c,# Si Li, a,b Jinbao Hou,d Huazhang Zhao *a,b a Department of Environmental Engineering, Peking University, Beijing 100871, China b The Key Laboratory of Water and Sediment Sciences, Ministry of Education, Beijing 100871, China c State Key Laboratory of Heavy Oil Processing, Beijing Key Laboratory of Oil and Gas Pollution Control, China University of Petroleum, 18 Fuxue Road, Changping District, Beijing 102249, China d College of Chemical Engineering, Beijing University of Chemical Technology, Beijing 100029, China # Co-first author. * Corresponding author. Tel/fax: +86-10-62758748; email address: [email protected] (H.Z. Zhao). S1 Experimental Methods 1. Preparation of graphite oxide (GO) Graphite oxide was prepared from natural graphite (Jinglong Co., Beijing, China) according to 1 a modified Hummers method : 120 mL 98 wt% H2SO4 was poured into a beaker containing a mixture of 5 g natural graphite and 2.5 g NaNO3, and then the mixture was stirred in an ice bath for 30 min. 15 g KMnO4 was added slowly into the mixture, which was allowed to react for 2 h at a temperature no more than 20°C. Then, the temperature was risen to 35°C, and the reaction was performed for another 2 h. After that, the reactant mixture was poured slowly into 360 mL distilled water under violent stirring condition so as to control the temperature no more than 90°C, followed by further reaction at 75°C for 1 h.
    [Show full text]
  • Sections-A, B and C
    Science IX Sample Paper 7 Solved www.rava.org.in CLASS IX (2019-20) SCIENCE (CODE 086) SAMPLE PAPER-7 Time : 3 Hours Maximum Marks : 80 General Instructions : (i) The question paper comprises of three sections-A, B and C. Attempt all the sections. (ii) All questions are compulsory. (iii) Internal choice is given in each sections. (iv) All questions in Section A are one-mark questions comprising MCQ, VSA type and assertion-reason type questions. They are to be answered in one word or in one sentence. (v) All questions in Section B are three-mark, short-answer type questions. These are to be answered in about 50-60 words each. (vi) All questions in Section C are five-mark, long-answer type questions. These are to be answered in about 80-90 words each. (vii) This question paper consists of a total of 30 questions. 6. Who proposed the fluid mosaic model of protoplasm? [1] Section - A (a) Singer and Nicolson (b) Watson and Crick (c) Robert Hook (d) Robert Brown 1. Which of the following actions a force can do? [1] (a) Can move a stationary object. Ans : (a) Singer and Nicolson. (b) Can stop a moving object. or (c) Can change the speed of a moving object. Which of the following are complex tissues? (d) All of the above. (a) Xylem and Phloem Ans : (d) All of the above (b) Collenchyma and Sclerenchyma (c) Parenchyma and Collenchyma 2. Ozone layer protects us from which one of the (d) Xylem and Parenchyma following? [1] (a) X- rays.
    [Show full text]
  • Ammonia, Anhydrous Ama
    AMMONIA, ANHYDROUS AMA CAUTIONARY RESPONSE INFORMATION 4. FIRE HAZARDS 7. SHIPPING INFORMATION 4.1 Flash Point: 7.1 Grades of Purity: Commercial, industrial, Common Synonyms Liquefied compressed Colorless Ammonia odor Not flammable under conditions likely to refrigeration, electronic, and metaflurgical Liquid ammonia gas be encountered grades all have purity greater than 99.5% 4.2 Flammable Limits in Air: 15.50%- 7.2 Storage Temperature: Ambient for pressurized 27.00% ammonia; low temperature for ammonia at Floats and boils on water. Poisonous, visible vapor cloud is produced. 4.3 Fire Extinguishing Agents: Stop flow of atmospheric pressure Avoid contact with liquid and vapor. Keep people away. gas or liquid. Let fire burn. 7.3 Inert Atmosphere: No requirement Wear goggles, self-contained breathing apparatus, and rubber overclothing (including gloves). 4.4 Fire Extinguishing Agents Not to Be 7.4 Venting: Safety relief 250 psi for ammonia Stop discharge if possible. Used: None under pressure. Pressure-vacuum for Stay upwind and use water spray to ``knock down'' vapor. 4.5 Special Hazards of Combustion ammonia at atmospheric pressure. Call fire department. Products: Not pertinent Isolate and remove discharged material. 7.5 IMO Pollution Category: Currently not available 4.6 Behavior in Fire: Not pertinent Notify local health and pollution control agencies. 7.6 Ship Type: 2 4.7 Auto Ignition Temperature: 1204°F Protect water intakes. 7.7 Barge Hull Type: 2 4.8 Electrical Hazards: Class I, Group D Combustible. 4.9 Burning Rate: 1 mm/min. Fire 8. HAZARD CLASSIFICATIONS Wear goggles, self-contained breathing apparatus, and rubber over- 4.10 Adiabatic Flame Temperature: Currently clothing (including gloves).
    [Show full text]
  • HEATS of COMBUSTION of DIAMOND and of GRAPHITE by Ralph S
    r---------------___........,._ . _____~ ~_ U. S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS RESEARCH PAPER RP1140 Part of Journal of Research of the }.{ational Bureau of Standards, Volume 21, October 1938 HEATS OF COMBUSTION OF DIAMOND AND OF GRAPHITE By Ralph S. Jessup ABSTRACT Measurements were made of the heats of combustion of one artificial graphite, two natural graphites, and two samples of diamond. The bomb calorimeter used was calibrated electrically and by means of benzoic acid. The amount of reaction in each combustion experiment was determined from the mass of carbon dioxide formed. This method of determining the amount of reaction automatically eliminates the effect of unburned carbon and of some impurities. It was found, however, that results for different samples did not agree unless the samples were purified. Two methods of purification were used: (a) heating in vacuo to 1,800° C and (b) treatment with hydrochloric and hydrofluoric acids and subsequent heating in vacuo to 200° C to remove traces of the acids. Both methods yielded graphite containing only small amounts of impurities. The mean value obtained for the heat of combustion (-/lH) of the purified graphites in oxygen at 25° C and a constant pressure of 1 atmosphere to form gaseous carbon dioxide at the same temperature and pressure was 393.396 international kilojoules per mole (44.010 g of CO2). The maximum deviation of the mean value for anyone of the purified samples from this value was 0.021 percent. The two samples of diamond, purified by treatment with aqueous hydrochloric and hydrofluoric acids and subsequently heated in vacuo to about 570° C, had average particle sizes of 2.5 I'- and 39.5 1'-, respectively, and yielded the following respective mean values for the heat of combustion (-/lH) at 25° C and 1 atmos­ phere, in oxygen to form gaseous carbon dioxide: 395.771 and 395.287 interna­ tional kilojoules per mole.
    [Show full text]
  • Thermochemistry of Heteroatomic Compounds:Calculation of the Heat
    Open Journal of Physical Chemistry, 2011, 1, 1-5 doi:10.4236/ojpc.2011.11001 Published Online May 2011 (http://www.SciRP.org/journal/ojpc) Thermochemistry of Heteroatomic Compounds: Calculation of the heat of Combustion and the heat of Formation of some Bioorganic Molecules with Different Hydrophenanthrene Rows Vitaly V. Ovchinnikov Tupolev Kazan State Technical University, St- K. Marks 10, 420111 Kazan, Russian Federation E-mail: [email protected] Received March 23rd, 2011; revised April 10th, 2011; accepted May 10th, 2011. Abstract On the basis of the known experimental heats of combustions of the seventeen alkanes in condensed state, the general equation comb HifNg has been deduced, in which i and f are correlation coefficients, N and g are a numbers of valence electrons and lone electron pairs of heteroatoms in molecule. The pre- sented dependence has been used for the calculation of the heats of combustion of thirteen organic molecules with biochemical properties: holestan, cholesterol, methyl-cholesterol, ergosterol, vitamin-D2, estradiol, an- drostenone, testosterone, androstanedione, morphine, morphinanone, codeine and pentasozine. It is noted that good convergence was obtained within the limits of errors of thermochemical experiments known in the literature and calculations of the heats of combustion for some of them were conducted. With the application of Hess law and the heats of vaporization vap H , which has been calculated with the use of a topological 1 s solvation index of the first order x , the heats of formation f H for condensed and gaseous phases were calculated for the listed bioorganic molecules. Keywords: Alkanes, Biochemical Molecules, the Heat of Combustion, Heat of Formation, Heat of Vaporiza- tion, Topological Solvation Index 1.
    [Show full text]
  • Measurements of Higher Alkanes Using NO Chemical Ionization in PTR-Tof-MS
    Atmos. Chem. Phys., 20, 14123–14138, 2020 https://doi.org/10.5194/acp-20-14123-2020 © Author(s) 2020. This work is distributed under the Creative Commons Attribution 4.0 License. Measurements of higher alkanes using NOC chemical ionization in PTR-ToF-MS: important contributions of higher alkanes to secondary organic aerosols in China Chaomin Wang1,2, Bin Yuan1,2, Caihong Wu1,2, Sihang Wang1,2, Jipeng Qi1,2, Baolin Wang3, Zelong Wang1,2, Weiwei Hu4, Wei Chen4, Chenshuo Ye5, Wenjie Wang5, Yele Sun6, Chen Wang3, Shan Huang1,2, Wei Song4, Xinming Wang4, Suxia Yang1,2, Shenyang Zhang1,2, Wanyun Xu7, Nan Ma1,2, Zhanyi Zhang1,2, Bin Jiang1,2, Hang Su8, Yafang Cheng8, Xuemei Wang1,2, and Min Shao1,2 1Institute for Environmental and Climate Research, Jinan University, 511443 Guangzhou, China 2Guangdong-Hongkong-Macau Joint Laboratory of Collaborative Innovation for Environmental Quality, 511443 Guangzhou, China 3School of Environmental Science and Engineering, Qilu University of Technology (Shandong Academy of Sciences), 250353 Jinan, China 4State Key Laboratory of Organic Geochemistry and Guangdong Key Laboratory of Environmental Protection and Resources Utilization, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, 510640 Guangzhou, China 5State Joint Key Laboratory of Environmental Simulation and Pollution Control, College of Environmental Sciences and Engineering, Peking University, 100871 Beijing, China 6State Key Laboratory of Atmospheric Boundary Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese
    [Show full text]
  • Thermal Properties of Petroleum Products
    UNITED STATES DEPARTMENT OF COMMERCE BUREAU OF STANDARDS THERMAL PROPERTIES OF PETROLEUM PRODUCTS MISCELLANEOUS PUBLICATION OF THE BUREAU OF STANDARDS, No. 97 UNITED STATES DEPARTMENT OF COMMERCE R. P. LAMONT, Secretary BUREAU OF STANDARDS GEORGE K. BURGESS, Director MISCELLANEOUS PUBLICATION No. 97 THERMAL PROPERTIES OF PETROLEUM PRODUCTS NOVEMBER 9, 1929 UNITED STATES GOVERNMENT PRINTING OFFICE WASHINGTON : 1929 F<ir isale by tfttf^uperintendent of Dotmrtients, Washington, D. C. - - - Price IS cants THERMAL PROPERTIES OF PETROLEUM PRODUCTS By C. S. Cragoe ABSTRACT Various thermal properties of petroleum products are given in numerous tables which embody the results of a critical study of the data in the literature, together with unpublished data obtained at the Bureau of Standards. The tables contain what appear to be the most reliable values at present available. The experimental basis for each table, and the agreement of the tabulated values with experimental results, are given. Accompanying each table is a statement regarding the esti- mated accuracy of the data and a practical example of the use of the data. The tables have been prepared in forms convenient for use in engineering. CONTENTS Page I. Introduction 1 II. Fundamental units and constants 2 III. Thermal expansion t 4 1. Thermal expansion of petroleum asphalts and fluxes 6 2. Thermal expansion of volatile petroleum liquids 8 3. Thermal expansion of gasoline-benzol mixtures 10 IV. Heats of combustion : 14 1. Heats of combustion of crude oils, fuel oils, and kerosenes 16 2. Heats of combustion of volatile petroleum products 18 3. Heats of combustion of gasoline-benzol mixtures 20 V.
    [Show full text]
  • Supporting Information for Modeling the Formation and Composition Of
    Supporting Information for Modeling the Formation and Composition of Secondary Organic Aerosol from Diesel Exhaust Using Parameterized and Semi-explicit Chemistry and Thermodynamic Models Sailaja Eluri1, Christopher D. Cappa2, Beth Friedman3, Delphine K. Farmer3, and Shantanu H. Jathar1 1 Department of Mechanical Engineering, Colorado State University, Fort Collins, CO, USA, 80523 2 Department of Civil and Environmental Engineering, University of California Davis, Davis, CA, USA, 95616 3 Department of Chemistry, Colorado State University, Fort Collins, CO, USA, 80523 Correspondence to: Shantanu H. Jathar ([email protected]) Table S1: Mass speciation and kOH for VOC emissions profile #3161 3 -1 - Species Name kOH (cm molecules s Mass Percent (%) 1) (1-methylpropyl) benzene 8.50×10'() 0.023 (2-methylpropyl) benzene 8.71×10'() 0.060 1,2,3-trimethylbenzene 3.27×10'(( 0.056 1,2,4-trimethylbenzene 3.25×10'(( 0.246 1,2-diethylbenzene 8.11×10'() 0.042 1,2-propadiene 9.82×10'() 0.218 1,3,5-trimethylbenzene 5.67×10'(( 0.088 1,3-butadiene 6.66×10'(( 0.088 1-butene 3.14×10'(( 0.311 1-methyl-2-ethylbenzene 7.44×10'() 0.065 1-methyl-3-ethylbenzene 1.39×10'(( 0.116 1-pentene 3.14×10'(( 0.148 2,2,4-trimethylpentane 3.34×10'() 0.139 2,2-dimethylbutane 2.23×10'() 0.028 2,3,4-trimethylpentane 6.60×10'() 0.009 2,3-dimethyl-1-butene 5.38×10'(( 0.014 2,3-dimethylhexane 8.55×10'() 0.005 2,3-dimethylpentane 7.14×10'() 0.032 2,4-dimethylhexane 8.55×10'() 0.019 2,4-dimethylpentane 4.77×10'() 0.009 2-methylheptane 8.28×10'() 0.028 2-methylhexane 6.86×10'()
    [Show full text]
  • Chapter Two Properties of Ammonia
    Chapter Two Properties of Ammonia Physical Properties General Anhydrous ammonia exists as either a colorless gas, colorless liquid, or white solid, depending on its pressure and temperature. In nearly all commonly encountered situations, it exists as either a liquid or a gas. The gas is less dense than air and the liquid is less dense than water at standard conditions. Ammonia gas (vapor) diffuses readily in air and the liquid is highly soluble in water with an accompanying release of heat. Ammonia exhibits classical saturation relationships whereby pressure and temperature are directly related so long as both the vapor and liquid phase are present. It does have a critical pressure and temperature. At atmospheric pressure, a closed container of ammonia vapor and liquid will be in equilibrium at a temperature of –28°F [–33°C]. It should be noted however that if liquid ammonia is spilled or released to the atmosphere at normal temperatures, the resultant pool of boiling liquid will be significantly colder than –28°F due to the law of partial pressures (the partial pressure of the ammonia vapor in the air near the liquid surface will be less than atmospheric pressure). The following table provides some of the important physical properties of ammonia. TABLE 2-1 Physical Properties of Ammonia Property Condition Value (IP) Value (SI) Molecular Weight 17.03 17.03 Color None None Physical State Room Temp Gas Gas Freezing Point P=1 atm –108°F –78°C Boiling Point P=1 atm –28.1°F –33.3°C Critical Pressure 1657 psia 11,410 kPa Critical Temp 271°F
    [Show full text]
  • Vapor Pressures and Vaporization Enthalpies of the N-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography
    BATCH: je1a04 USER: jeh69 DIV: @xyv04/data1/CLS_pj/GRP_je/JOB_i01/DIV_je0301747 DATE: October 17, 2003 1 Vapor Pressures and Vaporization Enthalpies of the n-Alkanes from 2 C21 to C30 at T ) 298.15 K by Correlation Gas Chromatography 3 James S. Chickos* and William Hanshaw 4 Department of Chemistry and Biochemistry, University of MissourisSt. Louis, St. Louis, Missouri 63121 5 6 The temperature dependence of gas chromatographic retention times for n-heptadecane to n-triacontane 7 is reported. These data are used to evaluate the vaporization enthalpies of these compounds at T ) 298.15 8 K, and a protocol is described that provides vapor pressures of these n-alkanes from T ) 298.15 to 575 9 K. The vapor pressure and vaporization enthalpy results obtained are compared with existing literature 10 data where possible and found to be internally consistent. Sublimation enthalpies for n-C17 to n-C30 are 11 calculated by combining vaporization enthalpies with fusion enthalpies and are compared when possible 12 to direct measurements. 13 14 Introduction 15 The n-alkanes serve as excellent standards for the 16 measurement of vaporization enthalpies of hydrocarbons.1,2 17 Recently, the vaporization enthalpies of the n-alkanes 18 reported in the literature were examined and experimental 19 values were selected on the basis of how well their 20 vaporization enthalpies correlated with their enthalpies of 21 transfer from solution to the gas phase as measured by gas 22 chromatography.3 A plot of the vaporization enthalpies of 23 the n-alkanes as a function of the number of carbon atoms 24 is given in Figure 1.
    [Show full text]
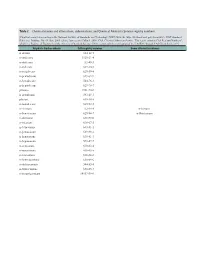
  • Table 2. Chemical Names and Alternatives, Abbreviations, and Chemical Abstracts Service Registry Numbers
    Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers. [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No. 69, June 2005 release, last accessed May 9, 2008. CAS, Chemical Abstracts Service. This report contains CAS Registry Numbers®, which is a Registered Trademark of the American Chemical Society. CAS recommends the verification of the CASRNs through CAS Client ServicesSM] Aliphatic hydrocarbons CAS registry number Some alternative names n-decane 124-18-5 n-undecane 1120-21-4 n-dodecane 112-40-3 n-tridecane 629-50-5 n-tetradecane 629-59-4 n-pentadecane 629-62-9 n-hexadecane 544-76-3 n-heptadecane 629-78-7 pristane 1921-70-6 n-octadecane 593-45-3 phytane 638-36-8 n-nonadecane 629-92-5 n-eicosane 112-95-8 n-Icosane n-heneicosane 629-94-7 n-Henicosane n-docosane 629-97-0 n-tricosane 638-67-5 n-tetracosane 643-31-1 n-pentacosane 629-99-2 n-hexacosane 630-01-3 n-heptacosane 593-49-7 n-octacosane 630-02-4 n-nonacosane 630-03-5 n-triacontane 638-68-6 n-hentriacontane 630-04-6 n-dotriacontane 544-85-4 n-tritriacontane 630-05-7 n-tetratriacontane 14167-59-0 Table 2. Chemical names and alternatives, abbreviations, and Chemical Abstracts Service registry numbers.—Continued [Final list compiled according to the National Institute of Standards and Technology (NIST) Web site (http://webbook.nist.gov/chemistry/); NIST Standard Reference Database No.
    [Show full text]
  • 1 Volumetric Energy Density of Compressed Air and Compressed
    Volumetric Energy Density of Compressed Air and Compressed Methane. Volumetric energy density is a combination of the potential for mechanical work, w, done by the change in pressure (P), and volume (V), and the chemical heat, q, released from burning the gas. For example, compressed air at 2,900 psi (~197 atm) has an energy density of 0.1 MJ/L calculated from PV and compressed methane (at 2,900 psi) has an energy density of 8.0 MJ/L calculated from the combination of PV and heat of combustion (Eq. 1). Estimate of Pressure Immediately After Ignition. Using the unpressurized channel volume of 1.0 mL, and our theoretically estimated temperature immediately after ignition of 2,800 oC, we calculated the maximum pressure, using the ideal gas law, to be ~1 MPa (~140 psi). Though this value is an overestimate (it does not take into account the channel volume expansion and the gas cooling, a complex calculation that is beyond the scope of this paper), we use it to illustrate the quick impulse of high pressure to use a passive valving system to control the flow of gas out of the channel after combustion and cooling. Fabrication of the Robot. The elastomer we used for the actuation layer was a stiff silicone rubber (Dragon Skin 10, DS-10; Smooth-on, Inc.). This elastomer has a greater Young’s modulus than our previous choice for pneumatic actuation (Ecoflex 00-30; Smooth-on, Inc.); pneu-nets composed of DS-10 could withstand the large forces generated within the channels during the explosion better than Ecoflex; in addition, DS-10 has a high resilience, which allowed the pneu-nets to release stored elastic energy rapidly for propulsion (Fig.
    [Show full text]