Characterization of Intonation in Carnatic Music by Parametrizing Pitch Histograms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Syllabus for Post Graduate Programme in Music
1 Appendix to U.O.No.Acad/C1/13058/2020, dated 10.12.2020 KANNUR UNIVERSITY SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: MA MUSIC DEPARTMENT OF MUSIC KANNUR UNIVERSITY SWAMI ANANDA THEERTHA CAMPUS EDAT PO, PAYYANUR PIN: 670327 2 SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: M A (MUSIC) ABOUT THE DEPARTMENT. The Department of Music, Kannur University was established in 2002. Department offers MA Music programme and PhD. So far 17 batches of students have passed out from this Department. This Department is the only institution offering PG programme in Music in Malabar area of Kerala. The Department is functioning at Swami Ananda Theertha Campus, Kannur University, Edat, Payyanur. The Department has a well-equipped library with more than 1800 books and subscription to over 10 Journals on Music. We have gooddigital collection of recordings of well-known musicians. The Department also possesses variety of musical instruments such as Tambura, Veena, Violin, Mridangam, Key board, Harmonium etc. The Department is active in the research of various facets of music. So far 7 scholars have been awarded Ph D and two Ph D thesis are under evaluation. Department of Music conducts Seminars, Lecture programmes and Music concerts. Department of Music has conducted seminars and workshops in collaboration with Indira Gandhi National Centre for the Arts-New Delhi, All India Radio, Zonal Cultural Centre under the Ministry of Culture, Government of India, and Folklore Academy, Kannur. -

Rakti in Raga and Laya
VEDAVALLI SPEAKS Sangita Kalanidhi R. Vedavalli is not only one of the most accomplished of our vocalists, she is also among the foremost thinkers of Carnatic music today with a mind as insightful and uncluttered as her music. Sruti is delighted to share her thoughts on a variety of topics with its readers. Rakti in raga and laya Rakti in raga and laya’ is a swara-oriented as against gamaka- complex theme which covers a oriented raga-s. There is a section variety of aspects. Attempts have of exponents which fears that ‘been made to interpret rakti in the tradition of gamaka-oriented different ways. The origin of the singing is giving way to swara- word ‘rakti’ is hard to trace, but the oriented renditions. term is used commonly to denote a manner of singing that is of a Yo asau Dhwaniviseshastu highly appreciated quality. It swaravamavibhooshitaha carries with it a sense of intense ranjako janachittaanaam involvement or engagement. Rakti Sankarabharanam or Bhairavi? rasa raga udaahritaha is derived from the root word Tyagaraja did not compose these ‘ranj’ – ranjayati iti ragaha, ranjayati kriti-s as a cluster under the There is a reference to ‘dhwani- iti raktihi. That which is pleasing, category of ghana raga-s. Older visesha’ in this sloka from Brihaddcsi. which engages the mind joyfully texts record these five songs merely Scholars have suggested that may be called rakti. The term rakti dhwanivisesha may be taken th as Tyagaraja’ s compositions and is not found in pre-17 century not as the Pancharatna kriti-s. Not to connote sruti and that its texts like Niruktam, Vyjayanti and only are these raga-s unsuitable for integration with music ensures a Amarakosam. -
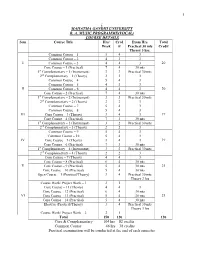
1 ; Mahatma Gandhi University B. A. Music Programme(Vocal
1 ; MAHATMA GANDHI UNIVERSITY B. A. MUSIC PROGRAMME(VOCAL) COURSE DETAILS Sem Course Title Hrs/ Cred Exam Hrs. Total Week it Practical 30 mts Credit Theory 3 hrs. Common Course – 1 5 4 3 Common Course – 2 4 3 3 I Common Course – 3 4 4 3 20 Core Course – 1 (Practical) 7 4 30 mts 1st Complementary – 1 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 1 (Theory) 2 2 3 Common Course – 4 5 4 3 Common Course – 5 4 3 3 II Common Course – 6 4 4 3 20 Core Course – 2 (Practical) 7 4 30 mts 1st Complementary – 2 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 2 (Theory) 2 2 3 Common Course – 7 5 4 3 Common Course – 8 5 4 3 III Core Course – 3 (Theory) 3 4 3 19 Core Course – 4 (Practical) 7 3 30 mts 1st Complementary – 3 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 3 (Theory) 2 2 3 Common Course – 9 5 4 3 Common Course – 10 5 4 3 IV Core Course – 5 (Theory) 3 4 3 19 Core Course – 6 (Practical) 7 3 30 mts 1st Complementary – 4 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 4 (Theory) 2 2 3 Core Course – 7 (Theory) 4 4 3 Core Course – 8 (Practical) 6 4 30 mts V Core Course – 9 (Practical) 5 4 30 mts 21 Core Course – 10 (Practical) 5 4 30 mts Open Course – 1 (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 1 2 1 Core Course – 11 (Theory) 4 4 3 Core Course – 12 (Practical) 6 4 30 mts VI Core Course – 13 (Practical) 5 4 30 mts 21 Core Course – 14 (Practical) 5 4 30 mts Elective (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 2 2 1 Total 150 120 120 Core & Complementary 104 hrs 82 credits Common Course 46 hrs 38 credits Practical examination will be conducted at the end of each semester 2 MAHATMA GANDHI UNIVERSITY B. -

Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan
Table of Contents From the Publications & Outreach Committee ..................................... Lakshmi Radhakrishnan ............ 1 From the President’s Desk ...................................................................... Balaji Raghothaman .................. 2 Connect with SRUTI ............................................................................................................................ 4 SRUTI at 30 – Some reflections…………………………………. ........... Mani, Dinakar, Uma & Balaji .. 5 A Mellifluous Ode to Devi by Sikkil Gurucharan & Anil Srinivasan… .. Kamakshi Mallikarjun ............. 11 Concert – Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan ..... 14 A Grand Violin Trio Concert ................................................................... Sneha Ramesh Mani ................ 16 What is in a raga’s identity – label or the notes?? ................................... P. Swaminathan ...................... 18 Saayujya by T.M.Krishna & Priyadarsini Govind ................................... Toni Shapiro-Phim .................. 20 And the Oscar goes to …… Kaapi – Bombay Jayashree Concert .......... P. Sivakumar ......................... 24 Saarangi – Harsh Narayan ...................................................................... Allyn Miner ........................... 26 Lec-Dem on Bharat Ratna MS Subbulakshmi by RK Shriramkumar .... Prabhakar Chitrapu ................ 28 Bala Bhavam – Bharatanatyam by Rumya Venkateshwaran ................. Roopa Nayak ......................... 33 Dr. M. Balamurali -

University of Kerala Ba Music Faculty of Fine Arts Choice
UNIVERSITY OF KERALA COURSE STRUCTURE AND SYLLABUS FOR BACHELOR OF ARTS DEGREE IN MUSIC BA MUSIC UNDER FACULTY OF FINE ARTS CHOICE BASED-CREDIT-SYSTEM (CBCS) Outcome Based Teaching, Learning and Evaluation (2021 Admission onwards) 1 Revised Scheme & Syllabus – 2021 First Degree Programme in Music Scheme of the courses Sem Course No. Course title Inst. Hrs Credit Total Total per week hours credits I EN 1111 Language course I (English I) 5 4 25 17 1111 Language course II (Additional 4 3 Language I) 1121 Foundation course I (English) 4 2 MU 1141 Core course I (Theory I) 6 4 Introduction to Indian Music MU 1131 Complementary I 3 2 (Veena) SK 1131.3 Complementary course II 3 2 II EN 1211 Language course III 5 4 25 20 (English III) EN1212 Language course IV 4 3 (English III) 1211 Language course V 4 3 (Additional Language II) MU1241 Core course II (Practical I) 6 4 Abhyasaganam & Sabhaganam MU1231 Complementary III 3 3 (Veena) SK1231.3 Complementary course IV 3 3 III EN 1311 Language course VI 5 4 25 21 (English IV) 1311 Language course VII 5 4 (Additional language III ) MU1321 Foundation course II 4 3 MU1341 Core course III (Theory II) 2 2 Ragam MU1342 Core course IV (Practical II) 3 2 Varnams and Kritis I MU1331 Complementary course V 3 3 (Veena) SK1331.3 Complementary course VI 3 3 IV EN 1411 Language course VIII 5 4 25 21 (English V) 1411 Language course IX 5 4 (Additional language IV) MU1441 Core course V (Theory III) 5 3 Ragam, Talam and Vaggeyakaras 2 MU1442 Core course VI (Practical III) 4 4 Varnams and Kritis II MU1431 Complementary -

June 2018 (Special Edition on Ganakaladhara Madurai Mani Iyer)
Lalitha Kala Tarangini Premier Quarterly Music Magazine from Sri Rama Lalitha Kala Mandira Volume 2018, Issue 2 June 2018 Sangeetha Kalarathna Titte Krishna Iyengar RR Keshavamurthy - The Lion of Karnataka DK Pattammal the Immortal legend Indian Music Experience (IME) Special Edition on Madurai Mani Iyer Raga Laya Prabha award felicitation Sri Rama Lalitha Kala Mandira awarded “Raaga Laya Prabha” on 13th May 2018 to Aditi B Prahalad (Vocal), BK Raghu (Violin) and Akshay Anand (Mridangam) who are the upcoming youngsters from Bangalore. This award is to commemorate the memory of the Founder-Director, Karnataka Kalashree GV Ranganayakamma, Vidushi GV Neela and her Sister, Founder-patron and Veena artiste Dr. GV Vijayalakshmi. The award carries a cash prize of Rs. Twenty Five Thousand and a citation. The award function was followed by a concert of Abhishek Raghuram (Vocal). B Vittal Rangan (Violin), NC Bharadwaj (Mridanga) and Guruprasanna (Kanjra) in presence of a capacity crowd. Left to Right Standing - Sri DR Srikantaiah - President, Akshay Anand, Sri GV Krishna Prasad - Hon. Secretary, Vidushi Neela Ramgopal,Vidwan Abhishek Raghuram, Aditi B Prahalad, BK Raghu June 2018 Titte Krishna Iyengar and RR Keshavamurthy. I am sure they will be an inspiration to the youngsters. Ganakaladhara Madurai Mani Iyer (MMI) shone like a jewel during the golden period of Karnatak music. He, Music world celebrated the centenary year of DK Pattam- along with GN Balasubramaniam (GN Sir) revolutionised mal a doyen in her own right on March 19, 2019. Vice karnatak music so much so that we talk about music in President of India, Shri M Venkaiah Naidu inaugurated the terms of before MMI, GN Sir and after MMI and GN Sir. -

Vol.74-76 2003-2005.Pdf
ISSN. 0970-3101 THE JOURNAL Of THE MUSIC ACADEMY MADRAS Devoted to the Advancement of the Science and Art of Music Vol. LXXIV 2003 ^ JllilPd frTBrf^ ^TTT^ II “I dwell not in Vaikunta, nor in the hearts of Yogins, not in the Sun; (but) where my Bhaktas sing, there be /, N arada !” Narada Bhakti Sutra EDITORIAL BOARD Dr. V.V. Srivatsa (Editor) N. Murali, President (Ex. Officio) Dr. Malathi Rangaswami (Convenor) Sulochana Pattabhi Raman Lakshmi Viswanathan Dr. SA.K. Durga Dr. Pappu Venugopala Rao V. Sriram THE MUSIC ACADEMY MADRAS New No. 168 (Old No. 306), T.T.K. Road, Chennai 600 014. Email : [email protected] Website : www.musicacademymadras.in ANNUAL SUBSCRIPTION - INLAND Rs. 150 FOREIGN US $ 5 Statement about ownership and other particulars about newspaper “JOURNAL OF THE MUSIC ACADEMY MADRAS” Chennai as required to be published under Section 19-D sub-section (B) of the Press and Registration Books Act read with rule 8 of the Registration of Newspapers (Central Rules) 1956. FORM IV JOURNAL OF THE MUSIC ACADEMY MADRAS Place of Publication Chennai All Correspondence relating to the journal should be addressed Periodicity of Publication and all books etc., intended for it should be sent in duplicate to the Annual Editor, The journal o f the Music Academy Madras, New 168 (Old 306), Printer Mr. N Subramanian T.T.K. Road, Chennai 600 014. 14, Neelakanta Mehta Street Articles on music and dance are accepted for publication on the T Nagar, Chennai 600 017 recommendation of the Editor. The Editor reserves the right to accept Publisher Dr. -

CARNATIC MUSIC (VOCAL) (Code No
CARNATIC MUSIC (VOCAL) (code no. 031) Class IX (2020-21) Theory Marks: 30 Time: 2 Hours No. of periods I. Brief history of Carnatic Music with special reference to Saint 10 Purandara dasa, Annamacharya, Bhadrachala Ramadasa, Saint Tyagaraja, Muthuswamy Dikshitar, Syama Sastry and Swati Tirunal. II. Definition of the following terms: 12 Sangeetam, Nada, raga, laya, Tala, Dhatu, Mathu, Sruti, Alankara, Arohana, Avarohana, Graha (Sama, Atita, Anagata), Svara – Prakruti & Vikriti Svaras, Poorvanga & Uttaranga, Sthayi, vadi, Samvadi, Anuvadi & Vivadi Svara – Amsa, Nyasa and Jeeva. III. Brief raga lakshanas of Mohanam, Hamsadhvani, Malahari, 12 Sankarabharanam, Mayamalavagoula, Bilahari, khamas, Kharaharapriya, Kalyani, Abhogi & Hindolam. IV. Brief knowledge about the musical forms. 8 Geetam, Svarajati, Svara Exercises, Alankaras, Varnam, Jatisvaram, Kirtana & Kriti. V. Description of following Talas: 8 Adi – Single & Double Kalai, Roopakam, Chapu – Tisra, Misra & Khanda and Sooladi Sapta Talas. VI. Notation of Gitams in Roopaka and Triputa Tala 10 Total Periods 60 CARNATIC MUSIC (VOCAL) Format of written examination for class IX Theory Marks: 30 Time: 2 Hours 1 Section I Six MCQ based on all the above mentioned topic 6 Marks 2 Section II Notation of Gitams in above mentioned Tala 6 Marks Writing of minimum Two Raga-lakshana from prescribed list in 6 Marks the syllabus. 3 Section III 6 marks Biography Musical Forms 4 Section IV 6 marks Description of talas, illustrating with examples Short notes of minimum 05 technical terms from the topic II. Definition of any two from the following terms (Sangeetam, Nada, Raga,Sruti, Alankara, Svara) Total Marks 30 marks Note: - Examiners should set atleast seven questions in total and the students should answer five questions from them, including two Essays, two short answer and short notes questions based on technical terms will be compulsory. -

Karnatak Music Vocal/Instrumental (Veena/ Violin )
Syllabus for M.A. (Previous) Karnatak Music Vocal/Instrumental (Veena/ Violin ) SEMESTER-I Core Course – 1 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Study of Scales, Ragas and Forms 70 Marks 1. Detailed study of ragas Prescribed (List – A). 2. Comparative study of the basic scales of different systems of Music such as Karnatak, Hindustani, Ancient Tamil Music, western and Far Eastern. 3. Decorative angas figuring in kriti’s and other Musical forms. 4. Pallavi notation; Theory of Rettai Pallavi and Nadai Pallavi. 5. Different Mudras figuring in Musical compositions. 6 Evolution of Indian Musical scales. Internal Assessment 30 Marks Core Course – 2 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Historical Study of the evolution of Ragas, Talas and Music Instruments 70 Marks 1. The different periods of Musical History and their distinctive features, Landmarks in the history of Indian Music. 2. Evolution of Ragas, Ragalakshana and system of Raga classification, Ragas which owe their origin to folk Music. 3. Classification of Musical Instruments. Important musical instruments adopted in traditional music. 4. Evolution of Musical forms with special reference to Prabandhas and their classifications; Gita Prabandha, Vadya Prabandha, Nritya Prabandha, and Misra Prabandha. 5. Concept of “Marga” and “Desi” in the spheres of Raga, Tala, Prabandha. 6. Knowledge about the formation of 175 and 108 systems of talas. Rare talas figure in Tiruppugazh. Core Course – 3 Practical Credit - 8 Practical : 70 Internal Assessment : 30 Maximum Marks : 100 Stage Performance 70 marks Performance of one hour duration with accompaniments, before an audience, planned by the candidate within the Prescribed Ragas(List A& B). -

Raga (Melodic Mode) Raga This Article Is About Melodic Modes in Indian Music
FREE SAMPLES FREE VST RESOURCES EFFECTS BLOG VIRTUAL INSTRUMENTS Raga (Melodic Mode) Raga This article is about melodic modes in Indian music. For subgenre of reggae music, see Ragga. For similar terms, see Ragini (actress), Raga (disambiguation), and Ragam (disambiguation). A Raga performance at Collège des Bernardins, France Indian classical music Carnatic music · Hindustani music · Concepts Shruti · Svara · Alankara · Raga · Rasa · Tala · A Raga (IAST: rāga), Raag or Ragam, literally means "coloring, tingeing, dyeing".[1][2] The term also refers to a concept close to melodic mode in Indian classical music.[3] Raga is a remarkable and central feature of classical Indian music tradition, but has no direct translation to concepts in the classical European music tradition.[4][5] Each raga is an array of melodic structures with musical motifs, considered in the Indian tradition to have the ability to "color the mind" and affect the emotions of the audience.[1][2][5] A raga consists of at least five notes, and each raga provides the musician with a musical framework.[3][6][7] The specific notes within a raga can be reordered and improvised by the musician, but a specific raga is either ascending or descending. Each raga has an emotional significance and symbolic associations such as with season, time and mood.[3] The raga is considered a means in Indian musical tradition to evoke certain feelings in an audience. Hundreds of raga are recognized in the classical Indian tradition, of which about 30 are common.[3][7] Each raga, state Dorothea -

Course Syllabus.Pdf
ANDHRA UNIVERSITY Regulations and Revised Syllabus Relating to Two Year M.A. (MUSIC) DEGREE EXAMINATION(SEMESTER SYSTEM) (WITH EFFECT FROM 2011-12) 1. Candidates for the Master of Arts Degree Examination shall be required : (a) To have passed the qualifying Examination of this University or an Examination of any other University recognized by the Academic Senate Equivalent thereto and : (b) To have undergone subsequently a further course of study extending over a period of two academic years in this University, each academic year consisting of two semesters ordinarily consecutive. 2. The course and scope of instruction shall be as defined in the syllabus prescribed. 3. (a) The candidates shall be required to take at the end of each semester of the Course of study an examination as detailed in the scheme for examination. (b) Candidates who have completed the first semester and have earned the necessary attendance and progress certificate shall be permitted to continue the second semester course irrespective of whether they have appeared or not at the previous examination. Such candidate may be permitted to appear for the 1st & 3rd semesters or 2nd & 4th semesters simultaneously. (c) Candidates appearing for the individual paper/papers shall obtain a minimum of 40% marks of each paper for a pass. The candidate shall be required to take at the end of the second year of the Course of study an examination as detailed in the scheme of examination. Each theory paper of the examination shall, unless otherwise prescribed be of three hours duration, and carry 100 marks. A candidate appearing for the whole examination shall be declared to have Passed the examination if he obtained not less than 40% of the total marks in all papers put together and also not less than 30% in the Semester end for a maximum of 100 marks in each paper. -

CARNATIC MUSIC (VOCAL) (Code No
CARNATIC MUSIC (VOCAL) (code no. 031) Class IX (2021-22) Theory Marks: 30 Time: 2 Hours No. of periods I. Brief history of Carnatic Music with special reference to Saint 10 Purandara dasa, Annamacharya, Bhadrachala Ramadasa, Saint Tyagaraja, Muthuswamy Dikshitar, Syama Sastry and Swati Tirunal. II. Definition of the following terms: 12 Sangeetam, Nada, raga, laya, Tala, Dhatu, Mathu, Sruti, Alankara, Arohana, Avarohana, Graha (Sama, Atita, Anagata), Svara – Prakruti & Vikriti Svaras, Poorvanga & Uttaranga, Sthayi, vadi, Samvadi, Anuvadi & Vivadi Svara – Amsa, Nyasa and Jeeva. III. Brief raga lakshanas of Mohanam, Hamsadhvani, Malahari, 12 Sankarabharanam, Mayamalavagoula, Bilahari, khamas, Kharaharapriya, Kalyani, Abhogi & Hindolam. IV. Brief knowledge about the musical forms. 8 Geetam, Svarajati, Svara Exercises, Alankaras, Varnam, Jatisvaram, Kirtana & Kriti. V. Description of following Talas: 8 Adi – Single & Double Kalai, Roopakam, Chapu – Tisra, Misra & Khanda and Sooladi Sapta Talas. VI. Notation of Gitams in Roopaka and Triputa Tala 10 Total Periods 60 CARNATIC MUSIC (VOCAL) Format of written examination for class IX Theory Marks: 30 Time: 2 Hours 1 Section I Six MCQ based on all the above mentioned topic 6 Marks 2 Section II Notation of Gitams in above mentioned Tala 6 Marks Writing of minimum Two Raga-lakshana from prescribed list in 6 Marks the syllabus. 3 Section III 6 marks Biography Musical Forms 4 Section IV 6 marks Description of talas, illustrating with examples Short notes of minimum 05 technical terms from the topic II. Definition of any two from the following terms (Sangeetam, Nada, Raga,Sruti, Alankara, Svara) Total Marks 30 marks Note: - Examiners should set atleast seven questions in total and the students should answer five questions from them, including two Essays, two short answer and short notes questions based on technical terms will be compulsory.