R¯Aga Identification Using Repetitive Note Patterns from Prescriptive
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Music Academy, Madras 115-E, Mowbray’S Road
Tyagaraja Bi-Centenary Volume THE JOURNAL OF THE MUSIC ACADEMY MADRAS A QUARTERLY DEVOTED TO THE ADVANCEMENT OF THE SCIENCE AND ART OF MUSIC Vol. XXXIX 1968 Parts MV srri erarfa i “ I dwell not in Vaikuntha, nor in the hearts of Yogins, nor in the Sun; (but) where my Bhaktas sing, there be I, Narada l ” EDITBD BY V. RAGHAVAN, M.A., p h .d . 1968 THE MUSIC ACADEMY, MADRAS 115-E, MOWBRAY’S ROAD. MADRAS-14 Annual Subscription—Inland Rs. 4. Foreign 8 sh. iI i & ADVERTISEMENT CHARGES ►j COVER PAGES: Full Page Half Page Back (outside) Rs. 25 Rs. 13 Front (inside) 20 11 Back (Do.) „ 30 „ 16 INSIDE PAGES: 1st page (after cover) „ 18 „ io Other pages (each) „ 15 „ 9 Preference will be given to advertisers of musical instruments and books and other artistic wares. Special positions and special rates on application. e iX NOTICE All correspondence should be addressed to Dr. V. Raghavan, Editor, Journal Of the Music Academy, Madras-14. « Articles on subjects of music and dance are accepted for mblication on the understanding that they are contributed solely o the Journal of the Music Academy. All manuscripts should be legibly written or preferably type written (double spaced—on one side of the paper only) and should >e signed by the writer (giving his address in full). The Editor of the Journal is not responsible for the views expressed by individual contributors. All books, advertisement moneys and cheques due to and intended for the Journal should be sent to Dr. V. Raghavan Editor. Pages. -

Syllabus for Post Graduate Programme in Music
1 Appendix to U.O.No.Acad/C1/13058/2020, dated 10.12.2020 KANNUR UNIVERSITY SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: MA MUSIC DEPARTMENT OF MUSIC KANNUR UNIVERSITY SWAMI ANANDA THEERTHA CAMPUS EDAT PO, PAYYANUR PIN: 670327 2 SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: M A (MUSIC) ABOUT THE DEPARTMENT. The Department of Music, Kannur University was established in 2002. Department offers MA Music programme and PhD. So far 17 batches of students have passed out from this Department. This Department is the only institution offering PG programme in Music in Malabar area of Kerala. The Department is functioning at Swami Ananda Theertha Campus, Kannur University, Edat, Payyanur. The Department has a well-equipped library with more than 1800 books and subscription to over 10 Journals on Music. We have gooddigital collection of recordings of well-known musicians. The Department also possesses variety of musical instruments such as Tambura, Veena, Violin, Mridangam, Key board, Harmonium etc. The Department is active in the research of various facets of music. So far 7 scholars have been awarded Ph D and two Ph D thesis are under evaluation. Department of Music conducts Seminars, Lecture programmes and Music concerts. Department of Music has conducted seminars and workshops in collaboration with Indira Gandhi National Centre for the Arts-New Delhi, All India Radio, Zonal Cultural Centre under the Ministry of Culture, Government of India, and Folklore Academy, Kannur. -

CARNATIC MUSIC (CODE – 032) CLASS – X (Melodic Instrument) 2020 – 21 Marking Scheme
CARNATIC MUSIC (CODE – 032) CLASS – X (Melodic Instrument) 2020 – 21 Marking Scheme Time - 2 hrs. Max. Marks : 30 Part A Multiple Choice Questions: Attempts any of 15 Question all are of Equal Marks : 1. Raga Abhogi is Janya of a) Karaharapriya 2. 72 Melakarta Scheme has c) 12 Chakras 3. Identify AbhyasaGhanam form the following d) Gitam 4. Idenfity the VarjyaSwaras in Raga SuddoSaveri b) GhanDharam – NishanDham 5. Raga Harikambhoji is a d) Sampoorna Raga 6. Identify popular vidilist from the following b) M. S. Gopala Krishnan 7. Find out the string instrument which has frets d) Veena 8. Raga Mohanam is an d) Audava – Audava Raga 9. Alankaras are set to d) 7 Talas 10 Mela Number of Raga Maya MalawaGoula d) 15 11. Identify the famous flutist d) T R. Mahalingam 12. RupakaTala has AksharaKals b) 6 13. Indentify composer of Navagrehakritis c) MuthuswaniDikshitan 14. Essential angas of kriti are a) Pallavi-Anuppallavi- Charanam b) Pallavi –multifplecharanma c) Pallavi – MukkyiSwaram d) Pallavi – Charanam 15. Raga SuddaDeven is Janya of a) Sankarabharanam 16. Composer of Famous GhanePanchartnaKritis – identify a) Thyagaraja 17. Find out most important accompanying instrument for a vocal concert b) Mridangam 18. A musical form set to different ragas c) Ragamalika 19. Identify dance from of music b) Tillana 20. Raga Sri Ranjani is Janya of a) Karahara Priya 21. Find out the popular Vena artist d) S. Bala Chander Part B Answer any five questions. All questions carry equal marks 5X3 = 15 1. Gitam : Gitam are the simplest musical form. The term “Gita” means song it is melodic extension of raga in which it is composed. -
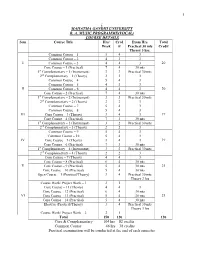
1 ; Mahatma Gandhi University B. A. Music Programme(Vocal
1 ; MAHATMA GANDHI UNIVERSITY B. A. MUSIC PROGRAMME(VOCAL) COURSE DETAILS Sem Course Title Hrs/ Cred Exam Hrs. Total Week it Practical 30 mts Credit Theory 3 hrs. Common Course – 1 5 4 3 Common Course – 2 4 3 3 I Common Course – 3 4 4 3 20 Core Course – 1 (Practical) 7 4 30 mts 1st Complementary – 1 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 1 (Theory) 2 2 3 Common Course – 4 5 4 3 Common Course – 5 4 3 3 II Common Course – 6 4 4 3 20 Core Course – 2 (Practical) 7 4 30 mts 1st Complementary – 2 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 2 (Theory) 2 2 3 Common Course – 7 5 4 3 Common Course – 8 5 4 3 III Core Course – 3 (Theory) 3 4 3 19 Core Course – 4 (Practical) 7 3 30 mts 1st Complementary – 3 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 3 (Theory) 2 2 3 Common Course – 9 5 4 3 Common Course – 10 5 4 3 IV Core Course – 5 (Theory) 3 4 3 19 Core Course – 6 (Practical) 7 3 30 mts 1st Complementary – 4 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 4 (Theory) 2 2 3 Core Course – 7 (Theory) 4 4 3 Core Course – 8 (Practical) 6 4 30 mts V Core Course – 9 (Practical) 5 4 30 mts 21 Core Course – 10 (Practical) 5 4 30 mts Open Course – 1 (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 1 2 1 Core Course – 11 (Theory) 4 4 3 Core Course – 12 (Practical) 6 4 30 mts VI Core Course – 13 (Practical) 5 4 30 mts 21 Core Course – 14 (Practical) 5 4 30 mts Elective (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 2 2 1 Total 150 120 120 Core & Complementary 104 hrs 82 credits Common Course 46 hrs 38 credits Practical examination will be conducted at the end of each semester 2 MAHATMA GANDHI UNIVERSITY B. -

Carnatic Music (Melodic Instrumental) (Code No
(B) CARNATIC MUSIC (MELODIC INSTRUMENTAL) (CODE NO. 032) CLASS–XI: (THEORY)(2019-20) One theory paper Total Marks: 100 2 Hours Marks : 30 Theory: A. History and Theory of Indian Music 1. (a) An outline knowledge of the following Lakshana Grandhas Silappadikaram, Natyasastra, Sangita Ratnakara and Chaturdandi Prakasika. (b) Short life sketch and contributions of the following:- Veena Dhanammal, flute Saraba Sastry, Rajamanikkam Pillai, Tirukkodi Kaval Krishna lyer (violin) Rajaratnam Pillai (Nagasvaram), Thyagaraja, Syamasastry, Muthuswamy Deekshitar, Veena Seshanna. (c) Brief study of the musical forms: Geetam and its varieties; Varnam – Padavarnam – Daruvarna Svarajati, Kriti/Kirtana and Padam 2. Definition and explanation of the following terms: Nada, Sruti, Svara, Vadi, Vivadi:, Samvadi, Anuvadi, Amsa & Nyasa, Jaati, Raga, Tala, Jati, Yati, Suladisapta talas, Nadai, Arohana, Avarohana. 3. Candidates should be able to write in notation the Varnam in the prescribed ragas. 4. Lakshanas of the ragas prescribed. 5. Talas Prescribed: Adi, Roopaka, Misra Chapu and Khanda Chapu. A brief study of Suladi Saptatalas. 6. A brief introduction to Manodhama Sangitam CLASS–XI (PRACTICAL) One Practical Paper Marks: 70 B. Practical Activities 1. Ragas Prescribed: Mayamalavagowla, Sankarabharana, Kharaharapriya, Kalyani, Kambhoji, Madhyamavati, Arabhi, Pantuvarali Kedaragaula, Vasanta, Anandabharavi, Kanada, Dhanyasi. 2. Varnams (atleast three) in Aditala in two degree of speed. 3. Kriti/Kirtana in each of the prescribed ragas, covering the main Talas Adi, Rupakam and Chapu. 4. Brief alapana of the ragas prescribed. 5. Technique of playing niraval and kalpana svaras in Adi, and Rupaka talas in two degrees of speed. 6. The candidate should be able to produce all the gamakas pertaining to the chosen instrument. -

Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan
Table of Contents From the Publications & Outreach Committee ..................................... Lakshmi Radhakrishnan ............ 1 From the President’s Desk ...................................................................... Balaji Raghothaman .................. 2 Connect with SRUTI ............................................................................................................................ 4 SRUTI at 30 – Some reflections…………………………………. ........... Mani, Dinakar, Uma & Balaji .. 5 A Mellifluous Ode to Devi by Sikkil Gurucharan & Anil Srinivasan… .. Kamakshi Mallikarjun ............. 11 Concert – Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan ..... 14 A Grand Violin Trio Concert ................................................................... Sneha Ramesh Mani ................ 16 What is in a raga’s identity – label or the notes?? ................................... P. Swaminathan ...................... 18 Saayujya by T.M.Krishna & Priyadarsini Govind ................................... Toni Shapiro-Phim .................. 20 And the Oscar goes to …… Kaapi – Bombay Jayashree Concert .......... P. Sivakumar ......................... 24 Saarangi – Harsh Narayan ...................................................................... Allyn Miner ........................... 26 Lec-Dem on Bharat Ratna MS Subbulakshmi by RK Shriramkumar .... Prabhakar Chitrapu ................ 28 Bala Bhavam – Bharatanatyam by Rumya Venkateshwaran ................. Roopa Nayak ......................... 33 Dr. M. Balamurali -

Evaluation of the Effects of Music Therapy Using Todi Raga of Hindustani Classical Music on Blood Pressure, Pulse Rate and Respiratory Rate of Healthy Elderly Men
Volume 64, Issue 1, 2020 Journal of Scientific Research Institute of Science, Banaras Hindu University, Varanasi, India. Evaluation of the Effects of Music Therapy Using Todi Raga of Hindustani Classical Music on Blood Pressure, Pulse Rate and Respiratory Rate of Healthy Elderly Men Samarpita Chatterjee (Mukherjee) 1, and Roan Mukherjee2* 1 Department of Hindustani Classical Music (Vocal), Sangit-Bhavana, Visva-Bharati (A Central University), Santiniketan, Birbhum-731235,West Bengal, India 2 Department of Human Physiology, Hazaribag College of Dental Sciences and Hospital, Demotand, Hazaribag 825301, Jharkhand, India. [email protected] Abstract Several studies have indicated that music therapy may affect I. INTRODUCTION cardiovascular health; in particular, it may bring positive changes Music may be regarded as the projection of ideas as well as in blood pressure levels and heart rate, thereby improving the emotions through significant sounds produced by an instrument, overall quality of life. Hence, to regulate blood pressure, music voices, or both by taking into consideration different elements of therapy may be regarded as a significant complementary and alternative medicine (CAM). The respiratory rate, if maintained melody, rhythm, and harmony. Music plays an important role in within the normal range, may promote good cardiac health. The everyone’s life. Music has the power to make one experience aim of the present study was to evaluate the changes in blood harmony, emotional ecstasy, spiritual uplifting, positive pressure, pulse rate and respiratory rate in healthy and disease-free behavioral changes, and absolute tranquility. The annoyance in males (age 50-60 years), at the completion of 30 days of music life may increase in lack of melody and harmony. -

Characterization of Intonation in Carnatic Music by Parametrizing Pitch Histograms
CHARACTERIZATION OF INTONATION IN CARNATIC MUSIC BY PARAMETRIZING PITCH HISTOGRAMS Gopala K. Koduri1, Joan Serra`2, and Xavier Serra1 1 Music Technology Group, Universitat Pompeu Fabra, Barcelona, Spain. 2 Artificial Intelligence Research Institute (IIIA-CSIC), Bellaterra, Barcelona, Spain. [email protected], [email protected], [email protected] ABSTRACT on the artist and the raaga [8, 15]. The study of intona- tion differs from that of tuning in its fundamental empha- Intonation is an important concept in Carnatic music that sis. When we talk about tuning we refer to the discrete is characteristic of a raaga, and intrinsic to the musical ex- frequencies with which we tune an instrument, thus it is pression of a performer. In this paper we approach the de- more of a theoretical concept than the one of intonation, scription of intonation from a computational perspective, with which we focus in the pitches used during a perfor- obtaining a compact representation of the pitch track of a mance. The two concepts are basically the same when we recording. First, we extract pitch contours from automat- study instruments that can only produce a fixed set of dis- ically selected voice segments. Then, we obtain a a pitch crete frequencies, like the piano. histogram of its full pitch-range, normalized by the tonic Given than in Indian music there is basically no instru- frequency, from which each prominent peak is automati- ment with fixed frequencies (the harmonium is an impor- cally labelled and parametrized. We validate such parame- tant exception), in practice tuning and intonation can be trization by considering an explorative classification task: considered the same. -

Andhra University 1 Year Diploma in (Music) Syllabus
SCHOOL OF DISTANCE EDUCATIN – ANDHRA UNIVERSITY 1st YEAR DIPLOMA IN (MUSIC) SYLLABUS (BOS approved and modified syllabus to be implemented from the admitted Batch 2012-13) Theory 100 Marks Paper I : Technical aspects of South Indian Classical Music 1. Technical Terms: a) Nada b) Sruti c) Swaras d) Swarasthanas e) Sathayi 2. Tala System: Sapta Talas, 35 Talas, Tala Dasa Prans, Chapu Tala Varieties Desadi and Madhyadi Talas 3. Musical Forms and their Lakshnas: Gitam, Varnam, Kritis, Kirtana, Padam, Ragamalika, Jasti Swaram, Swarajati, Tillana and Javali. 4. Lakshanas and Sancharas of the following Ragas: A a) Todi, b) Mayamalavagoula, c) Bhairavi, d) Kambhoji, e) Sankarabharanam f) Kalyani, g) Kharaharapriya, h) Mohana, i) Madhyamavathi j) Bilahari B. a) Dhanyasi, b) Saveri e)Vasanta d) HIndola e) Ananda Bhairavi f) Mukhari g) Kanada h) Khamas i) Begada j) Poorikalyani Paper II : Theoretical Aspects of South Indian Classical Music 100 Marks 1. Raaga and raga Lakshanam: a) Definition and Classification of ragas. b) Study of 13 Lakshanas c) ragalapana Padhathi 2. Musical Instruments and their classification 3. Special study of Tambura, Veena, Violin, Flute, Nagaswaram and Mridangam. 4. Characteristics of a composer. 5. Short biographical sketches of the following: a) Jayadeva b) Annamayya, c) Purandhara Dasa d) Narayana Tirtha e) Ramadasa f) Kshetrayya. Practical (First year) 100 Marks Paper III (Practical I) Fundamentals of Classical Music 1. a. Saraliswaras 6 b. Janta swaras 8 c. Alankaras 7 2. Gitas - 7 (Two Pillari Gitas, Two Ghanaraga Gitas, one Dhruva and one Lakshana gitam) 3. One Swarapallavi and one Swarajati 4. Five Adi Tala Varnas. -

CARNATIC MUSIC (CODE – 032) CLASS – X (Melodic Instrument) 2020 – 21 Sample Question Paper
CARNATIC MUSIC (CODE – 032) CLASS – X (Melodic Instrument) 2020 – 21 Sample Question Paper Time - 2 hrs. Max. Marks : 30 Part A Multiple Choice Questions: Attempts any of 15 Question all are of Equal Marks : 1. Raga Abhogi is Janya of a) Karaharapriya b) NataBhiravi c) HariKambhoji d) DheeraSankaraBharanam 2. 72 Melakarta Scheme has a) 6 Chakaras b) 9 Chakras c) 12 Chakras d) 36 Chakras 3. Identify AbhyasaGhanam form the following a) Kriti b) Raga Malika c) Tillana d) Gitam 4. Idenfity the VarjyaSwaras in Raga SuddoSaveri a) Madhyama – Nisha Dam b) GhanDharam – NishanDham c) NishaDham- Rishabam d) Dhaviatam – Nadgtanan 5. Raga Harikambhoji is a a) Audava Raga b) Shadava Raga c) Bhashanga Raga d) Sampoorna Raga 6. Identify popular vidilist from the following a) S BalaChander b) M. S. Gopala Krishnan c) G. N. BalaSubrmanyam d) PopanasamSiram 7. Find out the string instrument which has frets a) Violin b) Thanpur c) Sarangi d) Veena 8. Raga Mohanam is an a) Audav-Shadava Raga b) Shadava – Audava Raga c) Janaka- Raga d) Audava – Audava Raga 9. Alankaras are set to a) 9 Talas b) 5 Talas c) 6 Talas d) 7 Talas 10 .Mela Number of Raga Maya MalawaGoula a) 22 b) 28 c) 20 d) 15 11. Identify the famous flutist a) LalgadiJayaraman b) Papanaseem Sivan c) S. BalaChander d) T R. Mahalingam 12. RupakaTala has AksharaKals a) 3 b) 6 c) 9 d) 12 13. Indentify composer of Navagrehakritis a) Balamurali Krishna b) KoliswaraIyer c) MuthuswaniDikshitan d) G. N. Balasubramanam 14. Essential angas of kriti are a) Pallavi-Anuppallavi- Charanam b) Pallavi –multifplecharanma c) Pallavi – MukkyiSwaram d) Pallavi – Charanam 15. -

University of Kerala Ba Music Faculty of Fine Arts Choice
UNIVERSITY OF KERALA COURSE STRUCTURE AND SYLLABUS FOR BACHELOR OF ARTS DEGREE IN MUSIC BA MUSIC UNDER FACULTY OF FINE ARTS CHOICE BASED-CREDIT-SYSTEM (CBCS) Outcome Based Teaching, Learning and Evaluation (2021 Admission onwards) 1 Revised Scheme & Syllabus – 2021 First Degree Programme in Music Scheme of the courses Sem Course No. Course title Inst. Hrs Credit Total Total per week hours credits I EN 1111 Language course I (English I) 5 4 25 17 1111 Language course II (Additional 4 3 Language I) 1121 Foundation course I (English) 4 2 MU 1141 Core course I (Theory I) 6 4 Introduction to Indian Music MU 1131 Complementary I 3 2 (Veena) SK 1131.3 Complementary course II 3 2 II EN 1211 Language course III 5 4 25 20 (English III) EN1212 Language course IV 4 3 (English III) 1211 Language course V 4 3 (Additional Language II) MU1241 Core course II (Practical I) 6 4 Abhyasaganam & Sabhaganam MU1231 Complementary III 3 3 (Veena) SK1231.3 Complementary course IV 3 3 III EN 1311 Language course VI 5 4 25 21 (English IV) 1311 Language course VII 5 4 (Additional language III ) MU1321 Foundation course II 4 3 MU1341 Core course III (Theory II) 2 2 Ragam MU1342 Core course IV (Practical II) 3 2 Varnams and Kritis I MU1331 Complementary course V 3 3 (Veena) SK1331.3 Complementary course VI 3 3 IV EN 1411 Language course VIII 5 4 25 21 (English V) 1411 Language course IX 5 4 (Additional language IV) MU1441 Core course V (Theory III) 5 3 Ragam, Talam and Vaggeyakaras 2 MU1442 Core course VI (Practical III) 4 4 Varnams and Kritis II MU1431 Complementary -

Yuva Bharati Winner at the Khajuraho Festival in 1996
Ranjani Ramakrishnan (VIOLIN) Ranjani is the disciple of her mother Seetha Ramakrishnan. Ranjani won the prestigious Pt. Vishwanathdev Sharma Award and was also a Yuva Bharati winner at the Khajuraho Festival in 1996. Ranjani is a grade 'A artist Presents with AIR and Doordarshan. She has accompanied a number of Solitaire - Bharatnatyam Recital eminent and senior artistes. She also regularly accompanies Alarmel By Valli for her dance performances, in India and abroad. Shruti Abhishek and Meghah Vuppalapaty Followed by Divya Devaguptapu ‘s B Charles(LIGHTS AND STAGE MANAGER) Bhavanubhuti – Celebrating Kshetraya Charles is a sensitive Lighting and Stage director who works with several eminent dancers and theater artistes in Chennai. September 16 2017, 4:00 pm Mission Center of Performing Arts , Santa Clara , CA www.yuvabharati.org OUR NEXT CONCERT 1. Pushpanjali By Shruti and Meghah Talam: Adi Ragam : Gambheera Nattai Concept / Choreography: Smt. Janani Narayanan Sabda Manjari 2. Siva Sloka and Mallari By Shruti Talam: Adi Ragam : Hamir Kalyani , Nattai Concept / Choreography: Shri Vaibhav Arekar 3. Ranjani Mala By Meghah Talam: Adi Ragam : Ragamalika Composer: Tanjavur Shankara Iyer Concept / Choreography: Smt. Rukmini Vijayakumar 4. Ardhanariswara By Shruti Talam: Rupakam Ragam : Kumudakria Composer: Muthuswamy Dikshitar Concept / Choreography: Shri Vaibhav Arekar 5. Varnam- Swani Unnaiye Naan Megayum Nambinene By Meghah Talam: Adi Ragam : Reethigowla Composer: Vaidevelu Pillai Concept / Choreography: Smt. Rama Vaidyanathan 6. Ninda Stuti By Shruti Talam: Rupakam Ragam : Suruti Composer: Marimuthu Pillai Concept / Choreography: Shri Vaibhav Arekar Master's in Biotechnology and currently works at a Cancer diagnostics start-up in Menlo Park. 7. Thillana By Shruti Talam: Adi Ragam : Revati Shruti Abhishek Composer: Maduari N Krishnan Concept / Choreography: Shri Vaibhav Arekar Shruti is a Graduate in Performing Arts in Bharatanatyam with a Distinction from Nalanda Nrityakala Mahavidyala, Mumbai.