DOCSLIB.ORG

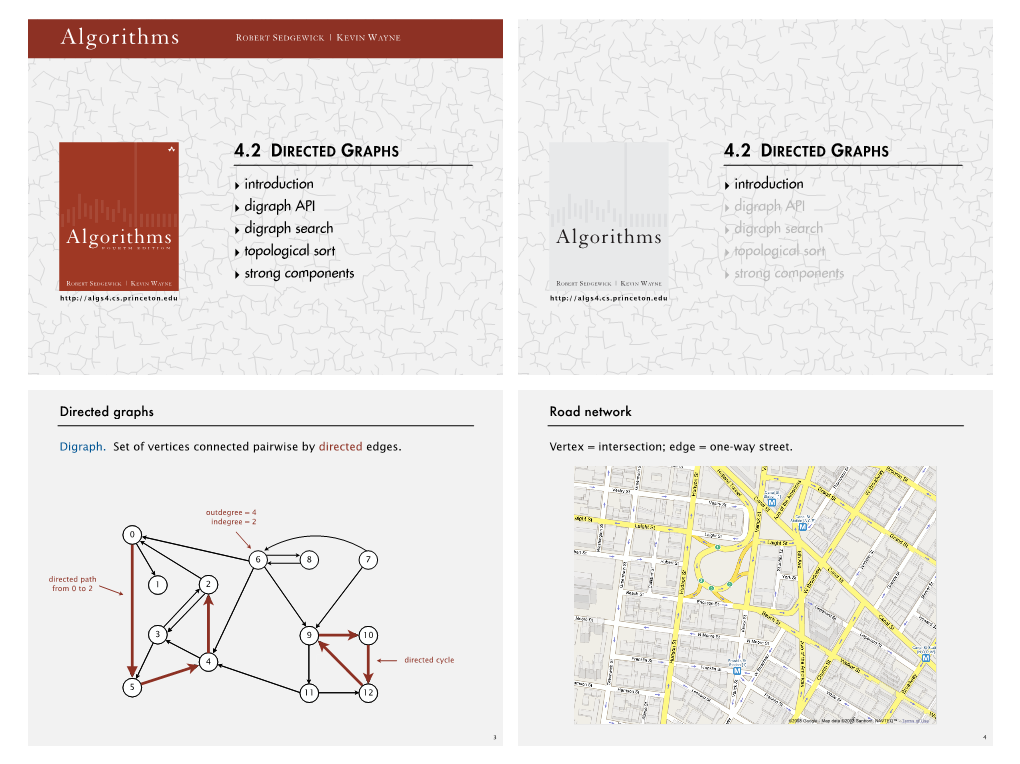
4.2 Directed Graphs 4.2 Directed Graphs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
4.2 Directed Graphs 4.2 Directed Graphs Algorithms ROBERT SEDGEWICK | KEVIN WAYNE 4.2 DIRECTED GRAPHS 4.2 DIRECTED GRAPHS ‣ introduction ‣ introduction ‣ digraph API ‣ digraph API Algorithms ‣ digraph search Algorithms ‣ digraph search FOURTH EDITION ‣ topological sort ‣ topological sort ‣ strong components ‣ strong components ROBERT SEDGEWICK | KEVIN WAYNE ROBERT SEDGEWICK | KEVIN WAYNE http://algs4.cs.princeton.edu http://algs4.cs.princeton.edu Directed graphs Road network To see all the details that are visible on the screen,use the Address Holland Tunnel "Print" link next to the map. New York, NY 10013 Digraph. Set of vertices connected pairwise by directed edges. Vertex = intersection; edge = one-way street. outdegree = 4 indegree = 2 0 6 8 7 directed path 2 from 0 to 2 1 3 9 10 4 directed cycle 5 11 12 ©2008 Google - Map data ©2008 Sanborn, NAVTEQ™ - Terms of Use 3 4 Political blogosphere graph Overnight interbank loan graph Vertex = political blog; edge = link. Vertex = bank; edge = overnight loan. GSCC GWCC GIN GOUT DC Tendril 4b`tqX #$ 4XWXqTe YtgWr gXsvhqd Yhq GXisXfUXq # 5Q11 & `bTgs vXTdex VhggXVsXW VhfihgXgs The Political Blogosphere and the 2004 U.S. Election: Divided They Blog, Adamic and Glance, 2005 The Topology of the Federal Funds Market, Bech and Atalay, 2008 Figure 1: Community structure of political blogs (expanded set), shown using utilizing a GEM 21 & WbrVhggXVsXW VhfihgXgs 5G11 & `bTgs rsqhg`ex VhggXVsXW VhfihgXgs 57B & `bTgs bgVhfihgXgs 5CIH & `bTgs hts VhfihgXgs Cg sabr WTx saXqX vXqX ! ghWXr bg saX 5G11 ghWXr bg saX 57B ! layout [11] in the GUESS[3] visualization and analysis tool. The colors reflect political orientation, 5 6 red for conservative, and blue for liberal. Orange links go from liberal to conservative, and purple ghWXr bg 5CIH ghWXr bg saX sXgWqber TgW ghWXr bg T WbrVhggXVsXW VhfihgXgs ones from conservative to liberal. The size of each blog reflects the number of other blogs that link to it. !"#$%&%'$( HaX ghWXr hY T gXsvhqd VTg UX iTqsbsbhgXW bgsh T VheeXVsbhg hY Wbrchbgs rXsr VTeeXW WbrVhggXVsXW Uber taxi graph VhfihgXgsrImplication!!"# graph!!" HaX ghWXr vbsabg XTVa WbrVhggXVsXW VhfihgXgs Wh ghs aTuX ebgdr sh hq Yqhf longer existed, or had moved to a different location. When looking at the front page of a blog we did ! ! ghWXr bg Tgx! hsaXq VhfihgXgs" ! bX !0 1" !1 0"$0 !!" 1 !!" # bY ) # ) HaX VhfihgXgs not make a distinction between blog references made in blogrolls (blogroll links) from those made ! !! ! vbsa saX eTq`Xrs gtfUXq hY ghWXr br qXYXqqXW# sh Tr saX$!)%*$& +"*,-.% $! /'$$"/&"0& /'12'$"$&' ( O5Q11P 7g hsaXq in posts (post citations). This had the disadvantage of not differentiating between blogs that were Vertex = taxi pickup; edge = taxi ride. vhqWrVertex saX = 5Q11 variable; br saX eTq`Xrsedge VhfihgXgs = logical hY saXimplication. gXsvhqd bg vabVa Tee ghWXr VhggXVs sh XTVa hsaXq ubT actively mentioned in a post on that day, from blogroll links that remain static over many weeks [10]. tgWbqXVsXW iTsar HaX qXfTbgbg` WbrVhggXVsXW VhfihgXgsr O21rP TqX rfTeeXq VhfihgXgsr Yhq vabVa saX Since posts usually contain sparse references to other blogs, and blogrolls usually contain dozens of rTfX br sqtX 7g XfibqbVTe rstWbXr saX 5Q11 br hYsXg YhtgW sh UX rXuXqTe hqWXqr hY fT`gbstWX eTq`Xq saTg blogs, we assumed that the network obtained by crawling the front page of each blog would strongly Tgx hY saX 21r OrXX 0qhWXq "& *-3 OPP reflect blogroll links. 479 blogs had blogrolls through blogrolling.com, while many others simply HaX 5Q11 Vhgrbrsr hY T )%*$& 4&5'$)-. /'$$"/&"0 /'12'$"$& O5G11P T )%*$& '6&7/'12'$"$& O5CIHP if x5 is true, maintained a list of links to their favorite blogs. We did not include blogrolls placed on a secondary T )%*$& %$7/'12'$"$& O57BP TgW &"$05%-4 OrXX 4b`tqX #P HaX 5G11 VhfiqbrXr Tee ghWXr saTs VTg qXTVa XuXqx then x0 is true page. hsaXq ghWX bg saX 5G11 saqht`a T WbqXVsXW iTsa ) ghWX br bg saX 5CIH bY bs aTr T iTsa Yqhf saX 5G11 We constructed a citation network by identifying whether a URL present on the page of one blog Uts ghs sh saX 5G11 7g VhgsqTrs T ghWX br bg~ saXx2 57B bY bsx aTr0 T iTsa sh saX 5G11 Uts ghs Yqhf bs ) references another political blog. We called a link found anywhere on a blog’s page, a “page link” to ghWX br bg T sXgWqbe bY bs WhXr ghs qXrbWX hg T WbqXVsXW iTsa sh hq Yqhf saX 5G11 distinguish it from a “post citation”, a link to another blog that occurs strictly within a post. Figure 1 !%4/644%'$( 7g saX gXsvhqd hY iTxfXgsr rXgs huXq 4XWvbqX TgTexyXW Ux GhqTfdb "& *-3 O P saX 5G11 shows the unmistakable division between the liberal and conservative political (blogo)spheres. In br saX eTq`Xrs VhfihgXgs Cg TuXqT`X Tefhrs %&' hY saX ghWXr bg saTs gXsvhqd UXehg` sh saX 5G11 7g fact, 91% of the links originating within either the conservative or liberal communities stay within VhgsqTrs saX 5G11 br ftVa rfTeeXq Yhq saX YXWXqTe YtgWr gXsvhqd 7g hgex (&' (' hY saX ghWXr x6 ~x4 x3 that community. An effect that may not be as apparent from the visualization is that even though UXehg` sh sabr VhfihgXgs 0x YTq saX eTq`Xrs VhfihgXgs br saX 57B 7g )%' )')hY saX ghWXr vXqX ) we started with a balanced set of blogs, conservative blogs show a greater tendency to link. 84% bg sabr VhfihgXgs HaX 5CIH VhgsTbgXW (*' +' hY Tee ghWXr iXq WTx vabeX saXqX vXqX (+' ,' hY ) ) of conservative blogs link to at least one other blog, and 82% receive a link. In contrast, 74% of saX ghWXr ehVTsXW bg saX sXgWqber @Xrr saTg -' (' hY saX ghWXr vXqX bg saX qXfTbgbg` WbrVhggXVsXW ) liberal blogs link to another blog, while only 67% are linked to by another blog. So overall, we see a VhfihgXgsr OrXX HTUeX P ~x5 ~x1 x1 x5 slightly higher tendency for conservative blogs to link. Liberal blogs linked to 13.6 blogs on average, HaX sXgWqber fTx Terh UX WbXqXgsbTsXW bgsh saqXX rtUVhfihgXgsr$ T rXs hY ghWXr saTs TqX hg T iTsa XfTgTsbg` Yqhf 57B T while conservative blogs linked to an average of 15.1, and this difference is almost entirely due to rXs hY ghWXr saTs TqX hg T iTsa eXTWbg` sh 5CIH TgW T rXs hY ghWXr saTs TqX hg T iTsa saTs UX`bgr bg 57B TgW XgWr bg 5CIH the higher proportion of liberal blogs with no links at all. !!"# hY ghWXr vXqX bg Yqhf57B sXgWqber $!%# hY ghWXr vXqX bg saX sh5CIH sXgWqber TgW "!&# hY ghWXr vXqX bg Although liberal blogs may not link as generously on average, the most popular liberal blogs, stUXr Yqhf 57B sh 5CIH Daily Kos and Eschaton (atrios.blogspot.com), had 338 and 264 links from our single-day snapshot ~x3 x4 ~x6 4 ~x0 x2 http://blog.uber.com/2012/01/09/uberdata-san-franciscomics/ 7 8 Combinational circuit WordNet graph Vertex = logical gate; edge = wire. Vertex = synset; edge = hypernym relationship. event happening occurrence occurrent natural_event miracle act human_acon human_acvity change alteraon modicaon miracle group_acon damage harm ..impairment transion increase forfeit forfeiture acon resistance opposion transgression leap jump saltaon jump leap change demoon variaon moon movement move locomoon travel descent run running jump parachung http://wordnet.princeton.edu dash sprint 9 10 Digraph applications Some digraph problems digraph vertex directed edge transportation street intersection one-way street problem description web web page hyperlink s→t path Is there a path from s to t ? food web species predator-prey relationship shortest s→t path What is the shortest path from s to t ? WordNet synset hypernym scheduling task precedence constraint directed cycle Is there a directed cycle in the graph ? financial bank transaction topological sort Can the digraph be drawn so that all edges point upwards? cell phone person placed call strong connectivity Is there a directed path between all pairs of vertices ? infectious disease person infection transitive closure For which vertices v and w is there a directed path from v to w ? game board position legal move citation journal article citation PageRank What is the importance of a web page ? object graph object pointer inheritance hierarchy class inherits from control flow code block jump 11 12 Digraph API Almost identical to Graph API. public class Digraph 4.2 DIRECTED GRAPHS Digraph(int V) create an empty digraph with V vertices Digraph(In in) create a digraph from input stream ‣ introduction void addEdge(int v, int w) add a directed edge v→w ‣ digraph API Iterable<Integer> adj(int v) vertices pointing from v ‣ digraph search Algorithms int V() number of vertices ‣ topological sort int E() number of edges ‣ strong components ROBERT SEDGEWICK | KEVIN WAYNE Digraph reverse() reverse of this digraph http://algs4.cs.princeton.edu String toString() string representation 14 Digraph API Digraph representation: adjacency lists % java Digraph tinyDG.txt tinyDG.txt Maintain vertex-indexed array of lists. V 0->5 5 1 13 E 22 0->1 tinyDG.txt V 5 1 4 2 2->0 13 adj[] E 2 3 2->3 0 3 tinyDG.txt 22 3 2 0 4 2 6 0 3->5 V 5 1 1 5 2 2 3 adj[] 0 1 3->2 13 0 3 E 3 2 0 2 0 2 4->3 22 11 12 3 2 6 0 3 1 5 2 12 9 4->2 4 2 0 1 9 10 4 5->4 4 2 3 2 0 adj[]2 9 11 11 12 3 0 2 3 5 ⋮ 3 7 9 3 2 12 9 0 6 9 4 8 0 10 12 11->4 6 0 9 10 4 4 11 4 7 11->12 9 11 1 5 5 2 4 3 6 9 0 1 7 9 8 12->9 9 4 8 0 3 5 2 0 10 12 2 6 6 8 9 6 11 12 11 4 7 3 2 8 6 10 4 3 3 6 9 5 4 8 ⋮ 12 9 3 5 0 5 11 11 10 6 8 4 9 6 4 12 9 10 6 4 6 9 12 8 6 10 In in = new In(args[0]); read digraph from 9 11 7 6 5 4 5 input stream 11 11 10 Digraph G = new Digraph(in); 4 12 7 9 0 5 10 12 6 4 6 12 9 4 8 0 6 9 12 for (int v = 0; v < G.V(); v++) 9 11 4 print out each 7 6 7 for (int w : G.adj(v)) 4 3 4 612 9 edge (once) 8 StdOut.println(v + "->" + w); 3 5 6 8 9 9 15 6 16 8 6 10 5 4 0 5 11 11 10 6 4 12 6 9 12 7 6 4 12 9 Digraph representations Adjacency-lists graph representation (review): Java implementation In practice.
Load more

Recommended publications
  • Applications of DFS
    (b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges 1 / 7 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 1 / 7 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 1 / 7 4. Connected components of a undirected graph (see Homework 6) 5.
    [Show full text]
  • Masters Thesis: an Approach to the Automatic Synthesis of Controllers with Mixed Qualitative/Quantitative Specifications
    An approach to the automatic synthesis of controllers with mixed qualitative/quantitative specifications. Athanasios Tasoglou Master of Science Thesis Delft Center for Systems and Control An approach to the automatic synthesis of controllers with mixed qualitative/quantitative specifications. Master of Science Thesis For the degree of Master of Science in Embedded Systems at Delft University of Technology Athanasios Tasoglou October 11, 2013 Faculty of Electrical Engineering, Mathematics and Computer Science (EWI) · Delft University of Technology *Cover by Orestis Gartaganis Copyright c Delft Center for Systems and Control (DCSC) All rights reserved. Abstract The world of systems and control guides more of our lives than most of us realize. Most of the products we rely on today are actually systems comprised of mechanical, electrical or electronic components. Engineering these complex systems is a challenge, as their ever growing complexity has made the analysis and the design of such systems an ambitious task. This urged the need to explore new methods to mitigate the complexity and to create sim- plified models. The answer to these new challenges? Abstractions. An abstraction of the the continuous dynamics is a symbolic model, where each “symbol” corresponds to an “aggregate” of states in the continuous model. Symbolic models enable the correct-by-design synthesis of controllers and the synthesis of controllers for classes of specifications that traditionally have not been considered in the context of continuous control systems. These include qualitative specifications formalized using temporal logics, such as Linear Temporal Logic (LTL). Be- sides addressing qualitative specifications, we are also interested in synthesizing controllers with quantitative specifications, in order to solve optimal control problems.
    [Show full text]
  • Efficient Graph Reachability Query Answering Using Tree Decomposition
    Efficient Graph Reachability Query Answering using Tree Decomposition Fang Wei Computer Science Department, University of Freiburg, Germany Abstract. Efficient reachability query answering in large directed graphs has been intensively investigated because of its fundamental importance in many application fields such as XML data processing, ontology rea- soning and bioinformatics. In this paper, we present a novel indexing method based on the concept of tree decomposition. We show analytically that this intuitive approach is both time and space efficient. We demonstrate empirically the efficiency and the effectiveness of our method. 1 Introduction Querying and manipulating large scale graph-like data has attracted much atten- tion in the database community, due to the wide application areas of graph data, such as GIS, XML databases, bioinformatics, social network, and ontologies. The problem of reachability test in a directed graph is among the fundamental operations on the graph data. Given a digraph G = (V; E) and u; v 2 V , a reachability query, denoted as u ! v, ask: is there a path from u to v? One of the fundamental queries on biological networks is for instance, to find all genes whose expressions are directly or indirectly influenced by a given molecule [15]. Given the graph representation of the genes and regulation events, the question can also be reduced to the reachability query in a directed graph. Recently, tree decomposition methodologies have been successfully applied to solving shortest path query answering over undirected graphs [17]. Briefly stated, the vertices in a graph G are decomposed into a tree in which each node contains a set of vertices in G.
    [Show full text]
  • Depth-First Search & Directed Graphs
    Depth-first Search and Directed Graphs Story So Far • Breadth-first search • Using breadth-first search for connectivity • Using bread-first search for testing bipartiteness BFS (G, s): Put s in the queue Q While Q is not empty Extract v from Q If v is unmarked Mark v For each edge (v, w): Put w into the queue Q The BFS Tree • Can remember parent nodes (the node at level i that lead us to a given node at level i + 1) BFS-Tree(G, s): Put (∅, s) in the queue Q While Q is not empty Extract (p, v) from Q If v is unmarked Mark v parent(v) = p For each edge (v, w): Put (v, w) into the queue Q Spanning Trees • Definition. A spanning tree of an undirected graph G is a connected acyclic subgraph of G that contains every node of G . • The tree produced by the BFS algorithm (with (( u, parent(u)) as edges) is a spanning tree of the component containing s . • The BFS spanning tree gives the shortest path from s to every other vertex in its component (we will revisit shortest path in a couple of lectures) • BFS trees in general are short and bushy Spanning Trees • Definition. A spanning tree of an undirected graph G is a connected acyclic subgraph of G that contains every node of G . • The tree produced by the BFS algorithm (with (( u, parent(u)) as edges) is a spanning tree of the component containing s . • The BFS spanning tree gives the shortest path from s to every other vertex in its component (we will revisit shortest path in a couple of lectures) • BFS trees in general are short and bushy Generalizing BFS: Whatever-First If we change how we store
    [Show full text]
  • 9 the Graph Data Model
    CHAPTER 9 ✦ ✦ ✦ ✦ The Graph Data Model A graph is, in a sense, nothing more than a binary relation. However, it has a powerful visualization as a set of points (called nodes) connected by lines (called edges) or by arrows (called arcs). In this regard, the graph is a generalization of the tree data model that we studied in Chapter 5. Like trees, graphs come in several forms: directed/undirected, and labeled/unlabeled. Also like trees, graphs are useful in a wide spectrum of problems such as com- puting distances, finding circularities in relationships, and determining connectiv- ities. We have already seen graphs used to represent the structure of programs in Chapter 2. Graphs were used in Chapter 7 to represent binary relations and to illustrate certain properties of relations, like commutativity. We shall see graphs used to represent automata in Chapter 10 and to represent electronic circuits in Chapter 13. Several other important applications of graphs are discussed in this chapter. ✦ ✦ ✦ ✦ 9.1 What This Chapter Is About The main topics of this chapter are ✦ The definitions concerning directed and undirected graphs (Sections 9.2 and 9.10). ✦ The two principal data structures for representing graphs: adjacency lists and adjacency matrices (Section 9.3). ✦ An algorithm and data structure for finding the connected components of an undirected graph (Section 9.4). ✦ A technique for finding minimal spanning trees (Section 9.5). ✦ A useful technique for exploring graphs, called “depth-first search” (Section 9.6). 451 452 THE GRAPH DATA MODEL ✦ Applications of depth-first search to test whether a directed graph has a cycle, to find a topological order for acyclic graphs, and to determine whether there is a path from one node to another (Section 9.7).
    [Show full text]
  • An Efficient Reachability Indexing Scheme for Large Directed Graphs
    1 Path-Tree: An Efficient Reachability Indexing Scheme for Large Directed Graphs RUOMING JIN, Kent State University NING RUAN, Kent State University YANG XIANG, The Ohio State University HAIXUN WANG, Microsoft Research Asia Reachability query is one of the fundamental queries in graph database. The main idea behind answering reachability queries is to assign vertices with certain labels such that the reachability between any two vertices can be determined by the labeling information. Though several approaches have been proposed for building these reachability labels, it remains open issues on how to handle increasingly large number of vertices in real world graphs, and how to find the best tradeoff among the labeling size, the query answering time, and the construction time. In this paper, we introduce a novel graph structure, referred to as path- tree, to help labeling very large graphs. The path-tree cover is a spanning subgraph of G in a tree shape. We show path-tree can be generalized to chain-tree which theoretically can has smaller labeling cost. On top of path-tree and chain-tree index, we also introduce a new compression scheme which groups vertices with similar labels together to further reduce the labeling size. In addition, we also propose an efficient incremental update algorithm for dynamic index maintenance. Finally, we demonstrate both analytically and empirically the effectiveness and efficiency of our new approaches. Categories and Subject Descriptors: H.2.8 [Database management]: Database Applications—graph index- ing and querying General Terms: Performance Additional Key Words and Phrases: Graph indexing, reachability queries, transitive closure, path-tree cover, maximal directed spanning tree ACM Reference Format: Jin, R., Ruan, N., Xiang, Y., and Wang, H.
    [Show full text]
  • A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph
    International Journal of Machine Learning and Computing, Vol. 4, No. 2, April 2014 A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph Renkun Liu then return error (graph has at Abstract—In a Directed Acyclic Graph (DAG), vertex A and least one cycle) vertex B are connected by a directed edge AB which shows that else return L (a topologically A comes before B in the ordering. In this way, we can find a sorted order) sorting algorithm totally different from Kahn or DFS algorithms, the directed edge already tells us the order of the Because we need to check every vertex and every edge for nodes, so that it can simply be sorted by re-ordering the nodes the “start nodes”, then sorting will check everything over according to the edges from a Direction Matrix. No vertex is again, so the complexity is O(E+V). specifically chosen, which makes the complexity to be O*E. An alternative algorithm for topological sorting is based on Then we can get an algorithm that has much lower complexity than Kahn and DFS. At last, the implement of the algorithm by Depth-First Search (DFS) [2]. For this algorithm, edges point matlab script will be shown in the appendix part. in the opposite direction as the previous algorithm. The algorithm loops through each node of the graph, in an Index Terms—DAG, algorithm, complexity, matlab. arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort: I.
    [Show full text]
  • The Surprizing Complexity of Generalized Reachability Games Nathanaël Fijalkow, Florian Horn
    The surprizing complexity of generalized reachability games Nathanaël Fijalkow, Florian Horn To cite this version: Nathanaël Fijalkow, Florian Horn. The surprizing complexity of generalized reachability games. 2010. hal-00525762v2 HAL Id: hal-00525762 https://hal.archives-ouvertes.fr/hal-00525762v2 Preprint submitted on 2 Feb 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The surprising complexity of generalized reachability games Nathanaël Fijalkow1,2 and Florian Horn1 1 LIAFA CNRS & Université Denis Diderot - Paris 7, France {nath,florian.horn}@liafa.jussieu.fr 2 ÉNS Cachan École Normale Supérieure de Cachan, France Abstract. Games on graphs provide a natural and powerful model for reactive systems. In this paper, we consider generalized reachability objectives, defined as conjunctions of reachability objectives. We first prove that deciding the winner in such games is PSPACE-complete, although it is fixed-parameter tractable with the number of reachability objectives as parameter. Moreover, we consider the memory requirements for both players and give matching upper and lower bounds on the size of winning strategies. In order to allow more efficient algorithms, we consider subclasses of generalized reachability games. We show that bounding the size of the reachability sets gives two natural subclasses where deciding the winner can be done efficiently.
    [Show full text]
  • CS302 Final Exam, December 5, 2016 - James S
    CS302 Final Exam, December 5, 2016 - James S. Plank Question 1 For each of the following algorithms/activities, tell me its running time with big-O notation. Use the answer sheet, and simply circle the correct running time. If n is unspecified, assume the following: If a vector or string is involved, assume that n is the number of elements. If a graph is involved, assume that n is the number of nodes. If the number of edges is not specified, then assume that the graph has O(n2) edges. A: Sorting a vector of uniformly distributed random numbers with bucket sort. B: In a graph with exactly one cycle, determining if a given node is on the cycle, or not on the cycle. C: Determining the connected components of an undirected graph. D: Sorting a vector of uniformly distributed random numbers with insertion sort. E: Finding a minimum spanning tree of a graph using Prim's algorithm. F: Sorting a vector of uniformly distributed random numbers with quicksort (average case). G: Calculating Fib(n) using dynamic programming. H: Performing a topological sort on a directed acyclic graph. I: Finding a minimum spanning tree of a graph using Kruskal's algorithm. J: Finding the minimum cut of a graph, after you have found the network flow. K: Finding the first augmenting path in the Edmonds Karp implementation of network flow. L: Processing the residual graph in the Ford Fulkerson algorithm, once you have found an augmenting path. Question 2 Please answer the following statements as true or false. A: Kruskal's algorithm requires a starting node.
    [Show full text]
  • Lecture 16: Directed Graphs
    Lecture 16: Directed Graphs BOS ORD JFK SFO DFW LAX MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and BFS Strong Connectivity Transitive Closure DAG and Toppgological Ordering 2 Digraphs A digraph is a ggpraph whose E edges are all directed D Short for “directed graph” C Applications B one-way streets A flights task scheduling 3 Digraph Properties E D A graph G=(V,E) such that Each edge goes in one direction: C Ed(dge (A,B) goes from A to B, Edge (B,A) goes from B to A, B If G is simple, m < n*(n-1). A If we keep in-edges and out-edges in separate adjacency lists, we can perform listing of in-edges and out-edges in time proportional to their size OutgoingEdges(A): (A,C), (A,D), (A,B) IngoingEdges(A): (E,A),(B,A) We say that vertex w is reachable from vertex v if there is a directed path from v to w EiseahablefomAE is reachable from A E is not reachable from D 4 Algorithm DFS(G, v) Directed DFS Input digraph G and a start vertex v of G Output traverses vertices in G reachable from v We can specialize the setLabel(v, VISITED) traversal algorithms (DFS and for all e ∈ G.outgoingEdges(v) BFS) to digraphs by traversing edges only along w ← opposite(v,e) their direction if getLabel(w) = UNEXPLORED DFS(G, w) In the directed DFS algorithm, we have 3 four types of edges E discovery edges 4 bkdback edges D forward edges cross edges A directed DFS starting at a C 2 vertex s visits all the vertices reachable from s B 5
    [Show full text]
  • An Efficient Strongly Connected Components Algorithm In
    An Efficient Strongly Connected Components Algorithm in the Fault Tolerant Model∗† Surender Baswana1, Keerti Choudhary2, and Liam Roditty3 1 Department of Computer Science and Engineering, IIT Kanpur, Kanpur, India [email protected] 2 Department of Computer Science and Engineering, IIT Kanpur, Kanpur, India [email protected] 3 Department of Computer Science, Bar Ilan University, Ramat Gan, Israel [email protected] Abstract In this paper we study the problem of maintaining the strongly connected components of a graph in the presence of failures. In particular, we show that given a directed graph G = (V, E) with n = |V | and m = |E|, and an integer value k ≥ 1, there is an algorithm that computes in O(2kn log2 n) time for any set F of size at most k the strongly connected components of the graph G \ F . The running time of our algorithm is almost optimal since the time for outputting the SCCs of G \ F is at least Ω(n). The algorithm uses a data structure that is computed in a preprocessing phase in polynomial time and is of size O(2kn2). Our result is obtained using a new observation on the relation between strongly connected components (SCCs) and reachability. More specifically, one of the main building blocks in our result is a restricted variant of the problem in which we only compute strongly connected com- ponents that intersect a certain path. Restricting our attention to a path allows us to implicitly compute reachability between the path vertices and the rest of the graph in time that depends logarithmically rather than linearly in the size of the path.
    [Show full text]
  • Merkle Trees and Directed Acyclic Graphs (DAG) As We've Discussed, the Decentralized Web Depends on Linked Data Structures
    Merkle trees and Directed Acyclic Graphs (DAG) As we've discussed, the decentralized web depends on linked data structures. Let's explore what those look like. Merkle trees A Merkle tree (or simple "hash tree") is a data structure in which every node is hashed. +--------+ | | +---------+ root +---------+ | | | | | +----+---+ | | | | +----v-----+ +-----v----+ +-----v----+ | | | | | | | node A | | node B | | node C | | | | | | | +----------+ +-----+----+ +-----+----+ | | +-----v----+ +-----v----+ | | | | | node D | | node E +-------+ | | | | | +----------+ +-----+----+ | | | +-----v----+ +----v-----+ | | | | | node F | | node G | | | | | +----------+ +----------+ In a Merkle tree, nodes point to other nodes by their content addresses (hashes). (Remember, when we run data through a cryptographic hash, we get back a "hash" or "content address" that we can think of as a link, so a Merkle tree is a collection of linked nodes.) As previously discussed, all content addresses are unique to the data they represent. In the graph above, node E contains a reference to the hash for node F and node G. This means that the content address (hash) of node E is unique to a node containing those addresses. Getting lost? Let's imagine this as a set of directories, or file folders. If we run directory E through our hashing algorithm while it contains subdirectories F and G, the content-derived hash we get back will include references to those two directories. If we remove directory G, it's like Grace removing that whisker from her kitten photo. Directory E doesn't have the same contents anymore, so it gets a new hash. As the tree above is built, the final content address (hash) of the root node is unique to a tree that contains every node all the way down this tree.
    [Show full text]