DOCSLIB.ORG

Algorithms (Winter 2021) Ungraded Problem Set 5 Due: Not for Submission Topic: Graphs: Basics + DFS

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Algorithms (Winter 2021) Ungraded Problem Set 5 Due: Not for Submission Topic: Graphs: Basics + DFS CS 31: Algorithms (Winter 2021) Ungraded Problem Set 5 Due: Not for submission Topic: Graphs: Basics + DFS Problem 1 (Some operations with graphs). For the parts below, describe your algorithm summary in English and also provide a clear pseudocode. You may assume the graph G = (V; E) is input as adjacency lists. a. In this part the graph G is directed. You need to return the reverse graph Grev where all edges have been reversed. Grev should also be represented as adjacency lists. What is the runtime of your algo- rithm? K b. Recall the definition of a walk from vertex u to vertex v and a path from vertex u to v. Design an algorithm which takes input a walk from u to v, and returns a path from u to v. K Problem 2 (DFS firsts and lasts). For each of the following assertions, prove or give a counterexample. The graph G, unless mentioned, is directed. When you give a counter-example, you should explain why it is a counter-example. (a) If G contains a path from u to v and if first[u] < first[v] in a depth-first search of G, then last[v] < last[u]. K (b) If (u=v1; v2; : : : ; vk =v) is a path from u to v in G such that last[vi] < last[v] for all 1 ≤ i < k, then first[v] < first[vi] for all 1 ≤ i < k. K (c) If we run depth-first search on G in an arbitrary order to obtain first’s and last’s, and let σ be the increasing order of last[v]’s. Then running DFS on G in this order returns the strongly connected components of G. K (d) Suppose we run DFS on a graph G with an arbitrary order, and let v be the vertex with the largest last[v]. Suppose u is a vertex and there is a path from u to v in G. Then there is a path from v to u in G as well. K Problem 3 (Counting number of paths in a DAG). KK Let G = (V; E) be a directed acyclic graph. Given two vertices s and t, count the number of paths from s to t using dynamic programming. The algorithm should run in O(m+n) time where jV j = n and jEj = m. Problem 4 (Cheapest Reachable Vertex). KK We are given a directed graph G = (V; E) with jV j = n and jEj = m. Each vertex v has a cost cost(v) which is a positive integer. You need to design an algorithm to output should be an array/dictionary cheapest indexed by the vertices of G, such that cheapest[u] should contain just the cost of the cheapest vertex reachable from u. a. Assume G is a directed acyclic graph and design an O(n+m) time dynamic programming algorithm. 1 b. Then, use this to give an O(n + m) time algorithm for any directed graph. Problem 5. This is another remarkable application of strongly connected components. For this exercise, it may be worthwhile to refresh your knowledge of Boolean variables and Propositional Logic from CS 30 In a 2SAT formula, you are given a set of clauses, where each clause is the disjunction (OR) of two literals (a literal is a Boolean variable or the negation of a Boolean variable). A 2SAT formula is satisfiable if there is a way to assign a value true or false to each of the variables so that all clauses are true , that is, there is at least one true literal in each clause. For example, here’s an example of a 2SAT formula: (x1 _ x2) ^ (x1 _ x3) ^ (x1 _ x2) ^ (x3 _ x4) ^ (x1 _ x4) (1) This formula is satisfiable since we can set x1; x2; x3; x4 to true ,false ,false , and true respectively. Note that all the clauses are satisfied, and thus the ^ of all these clauses are satisfied too. (a) Construct a 2SAT formula with four variables which is not satisfiable. K The 2SAT problem takes input a 2SAT formula and returns YES if it is satisfiable and NO if not. The purpose of this problem to solve the 2SAT problem via a reduction to the SCC problem. In particular, given a 2SAT formula with n variables and m clauses, construct the following directed graph G = (V; E). • G has 2n vertices, one for each variable xi and xi. • G has 2m directed edges: for each clause of the form (α _ β) (where α is either a variable or its negation), G has an edge from α to β and from β to α. Note that the clause (α _ β) is equivalent to either of the implications α ) β or β ) α. In this sense the above graph records all the implications. (b) Construct the graph G for the formula given above in (1). K (c) Prove that if G has a strongly connected component containing both the vertices x and x for some variable x, then the formula can have no satisfying assignment. KK (d) Now prove the negation: prove that if no strongly component of G has a variable and its negation, then the formula must be satisfiable. KKK Conclude that there is a O(n + m)-time algorithm for the 2SAT problem. 2.
Load more

Recommended publications
  • Applications of DFS
    (b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges 1 / 7 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 1 / 7 3. Topological sort of a DAG { next 4. Connected components of a undirected graph (see Homework 6) 5. Strongly connected components of a drected graph (see Sec.22.5 of [CLRS,3rd ed.]) Applications of DFS 1. For a undirected graph, (a) a DFS produces only Tree and Back edges (b) acyclic (tree) iff a DFS yeilds no Back edges 2.A directed graph is acyclic iff a DFS yields no back edges, i.e., DAG (directed acyclic graph) , no back edges 1 / 7 4. Connected components of a undirected graph (see Homework 6) 5.
    [Show full text]
  • 9 the Graph Data Model
    CHAPTER 9 ✦ ✦ ✦ ✦ The Graph Data Model A graph is, in a sense, nothing more than a binary relation. However, it has a powerful visualization as a set of points (called nodes) connected by lines (called edges) or by arrows (called arcs). In this regard, the graph is a generalization of the tree data model that we studied in Chapter 5. Like trees, graphs come in several forms: directed/undirected, and labeled/unlabeled. Also like trees, graphs are useful in a wide spectrum of problems such as com- puting distances, finding circularities in relationships, and determining connectiv- ities. We have already seen graphs used to represent the structure of programs in Chapter 2. Graphs were used in Chapter 7 to represent binary relations and to illustrate certain properties of relations, like commutativity. We shall see graphs used to represent automata in Chapter 10 and to represent electronic circuits in Chapter 13. Several other important applications of graphs are discussed in this chapter. ✦ ✦ ✦ ✦ 9.1 What This Chapter Is About The main topics of this chapter are ✦ The definitions concerning directed and undirected graphs (Sections 9.2 and 9.10). ✦ The two principal data structures for representing graphs: adjacency lists and adjacency matrices (Section 9.3). ✦ An algorithm and data structure for finding the connected components of an undirected graph (Section 9.4). ✦ A technique for finding minimal spanning trees (Section 9.5). ✦ A useful technique for exploring graphs, called “depth-first search” (Section 9.6). 451 452 THE GRAPH DATA MODEL ✦ Applications of depth-first search to test whether a directed graph has a cycle, to find a topological order for acyclic graphs, and to determine whether there is a path from one node to another (Section 9.7).
    [Show full text]
  • A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph
    International Journal of Machine Learning and Computing, Vol. 4, No. 2, April 2014 A Low Complexity Topological Sorting Algorithm for Directed Acyclic Graph Renkun Liu then return error (graph has at Abstract—In a Directed Acyclic Graph (DAG), vertex A and least one cycle) vertex B are connected by a directed edge AB which shows that else return L (a topologically A comes before B in the ordering. In this way, we can find a sorted order) sorting algorithm totally different from Kahn or DFS algorithms, the directed edge already tells us the order of the Because we need to check every vertex and every edge for nodes, so that it can simply be sorted by re-ordering the nodes the “start nodes”, then sorting will check everything over according to the edges from a Direction Matrix. No vertex is again, so the complexity is O(E+V). specifically chosen, which makes the complexity to be O*E. An alternative algorithm for topological sorting is based on Then we can get an algorithm that has much lower complexity than Kahn and DFS. At last, the implement of the algorithm by Depth-First Search (DFS) [2]. For this algorithm, edges point matlab script will be shown in the appendix part. in the opposite direction as the previous algorithm. The algorithm loops through each node of the graph, in an Index Terms—DAG, algorithm, complexity, matlab. arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort: I.
    [Show full text]
  • CS302 Final Exam, December 5, 2016 - James S
    CS302 Final Exam, December 5, 2016 - James S. Plank Question 1 For each of the following algorithms/activities, tell me its running time with big-O notation. Use the answer sheet, and simply circle the correct running time. If n is unspecified, assume the following: If a vector or string is involved, assume that n is the number of elements. If a graph is involved, assume that n is the number of nodes. If the number of edges is not specified, then assume that the graph has O(n2) edges. A: Sorting a vector of uniformly distributed random numbers with bucket sort. B: In a graph with exactly one cycle, determining if a given node is on the cycle, or not on the cycle. C: Determining the connected components of an undirected graph. D: Sorting a vector of uniformly distributed random numbers with insertion sort. E: Finding a minimum spanning tree of a graph using Prim's algorithm. F: Sorting a vector of uniformly distributed random numbers with quicksort (average case). G: Calculating Fib(n) using dynamic programming. H: Performing a topological sort on a directed acyclic graph. I: Finding a minimum spanning tree of a graph using Kruskal's algorithm. J: Finding the minimum cut of a graph, after you have found the network flow. K: Finding the first augmenting path in the Edmonds Karp implementation of network flow. L: Processing the residual graph in the Ford Fulkerson algorithm, once you have found an augmenting path. Question 2 Please answer the following statements as true or false. A: Kruskal's algorithm requires a starting node.
    [Show full text]
  • Merkle Trees and Directed Acyclic Graphs (DAG) As We've Discussed, the Decentralized Web Depends on Linked Data Structures
    Merkle trees and Directed Acyclic Graphs (DAG) As we've discussed, the decentralized web depends on linked data structures. Let's explore what those look like. Merkle trees A Merkle tree (or simple "hash tree") is a data structure in which every node is hashed. +--------+ | | +---------+ root +---------+ | | | | | +----+---+ | | | | +----v-----+ +-----v----+ +-----v----+ | | | | | | | node A | | node B | | node C | | | | | | | +----------+ +-----+----+ +-----+----+ | | +-----v----+ +-----v----+ | | | | | node D | | node E +-------+ | | | | | +----------+ +-----+----+ | | | +-----v----+ +----v-----+ | | | | | node F | | node G | | | | | +----------+ +----------+ In a Merkle tree, nodes point to other nodes by their content addresses (hashes). (Remember, when we run data through a cryptographic hash, we get back a "hash" or "content address" that we can think of as a link, so a Merkle tree is a collection of linked nodes.) As previously discussed, all content addresses are unique to the data they represent. In the graph above, node E contains a reference to the hash for node F and node G. This means that the content address (hash) of node E is unique to a node containing those addresses. Getting lost? Let's imagine this as a set of directories, or file folders. If we run directory E through our hashing algorithm while it contains subdirectories F and G, the content-derived hash we get back will include references to those two directories. If we remove directory G, it's like Grace removing that whisker from her kitten photo. Directory E doesn't have the same contents anymore, so it gets a new hash. As the tree above is built, the final content address (hash) of the root node is unique to a tree that contains every node all the way down this tree.
    [Show full text]
  • Graph Algorithms G
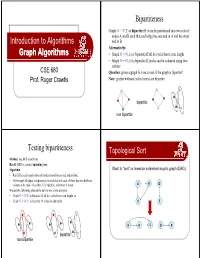
    Bipartiteness Graph G = (V,E) is bipartite iff it can be partitioned into two sets of nodes A and B such that each edge has one end in A and the other Introduction to Algorithms end in B Alternatively: Graph Algorithms • Graph G = (V,E) is bipartite iff all its cycles have even length • Graph G = (V,E) is bipartite iff nodes can be coloured using two colours CSE 680 Question: given a graph G, how to test if the graph is bipartite? Prof. Roger Crawfis Note: graphs without cycles (trees) are bipartite bipartite: non bipartite Testing bipartiteness Toppgological Sort Method: use BFS search tree Recall: BFS is a rooted spanning tree. Algorithm: Want to “sort” or linearize a directed acyygp()clic graph (DAG). • Run BFS search and colour all nodes in odd layers red, others blue • Go through all edges in adjacency list and check if each of them has two different colours at its ends - if so then G is bipartite, otherwise it is not A B D We use the following alternative definitions in the analysis: • Graph G = (V,E) is bipartite iff all its cycles have even length, or • Graph G = (V, E) is bipartite iff it has no odd cycle C E A B C D E bipartit e non bipartite Toppgological Sort Example z PerformedonaPerformed on a DAG. A B D z Linear ordering of the vertices of G such that if 1/ (u, v) ∈ E, then u appears before v. Topological-Sort (G) 1. call DFS(G) to compute finishing times f [v] for all v ∈ V 2.
    [Show full text]
  • 6.042J Chapter 6: Directed Graphs
    “mcs-ftl” — 2010/9/8 — 0:40 — page 189 — #195 6 Directed Graphs 6.1 Definitions So far, we have been working with graphs with undirected edges. A directed edge is an edge where the endpoints are distinguished—one is the head and one is the tail. In particular, a directed edge is specified as an ordered pair of vertices u, v and is denoted by .u; v/ or u v. In this case, u is the tail of the edge and v is the ! head. For example, see Figure 6.1. A graph with directed edges is called a directed graph or digraph. Definition 6.1.1. A directed graph G .V; E/ consists of a nonempty set of D nodes V and a set of directed edges E. Each edge e of E is specified by an ordered pair of vertices u; v V . A directed graph is simple if it has no loops (that is, edges 2 of the form u u) and no multiple edges. ! Since we will focus on the case of simple directed graphs in this chapter, we will generally omit the word simple when referring to them. Note that such a graph can contain an edge u v as well as the edge v u since these are different edges ! ! (for example, they have a different tail). Directed graphs arise in applications where the relationship represented by an edge is 1-way or asymmetric. Examples include: a 1-way street, one person likes another but the feeling is not necessarily reciprocated, a communication channel such as a cable modem that has more capacity for downloading than uploading, one entity is larger than another, and one job needs to be completed before another job can begin.
    [Show full text]
  • Graph Algorithms
    Graph Algorithms Graphs and Graph Repre- sentations Graph Graph Algorithms Traversals COMP4128 Programming Challenges Directed Graphs and Cycles Strongly Connected Components Example: School of Computer Science and Engineering 2SAT UNSW Australia Minimum Spanning Trees Table of Contents 2 Graph Algorithms 1 Graphs and Graph Representations Graphs and Graph Repre- sentations 2 Graph Graph Traversals Traversals Directed Graphs and 3 Directed Graphs and Cycles Cycles Strongly Connected 4 Strongly Connected Components Components Example: 2SAT 5 Example: 2SAT Minimum Spanning Trees 6 Minimum Spanning Trees Graphs 3 Graph Algorithms Graphs and Graph Repre- sentations A graph is a collection of vertices and edges connecting Graph pairs of vertices. Traversals Directed Generally, graphs can be thought of as abstract Graphs and Cycles representations of objects and connections between those Strongly objects, e.g. intersections and roads, people and Connected Components friendships, variables and equations. Example: Many unexpected problems can be solved with graph 2SAT techniques. Minimum Spanning Trees Graphs 4 Graph Algorithms Graphs and Graph Repre- sentations Graph Many different types of graphs Traversals Directed graphs Directed Graphs and Acyclic graphs, including trees Cycles Weighted graphs Strongly Connected Flow graphs Components Other labels for the vertices and edges Example: 2SAT Minimum Spanning Trees Graph Representations 5 Graph Algorithms Graphs and Graph Repre- sentations Graph You’ll usually want to either use an adjacency list or an Traversals adjacency matrix to store your graph. Directed Graphs and An adjacency matrix is just a table (usually implemented Cycles as an array) where the jth entry in the ith row represents Strongly Connected the edge from i to j, or lack thereof.
    [Show full text]
  • The Shortest Path Problem with Edge Information Reuse Is NP-Complete
    The Shortest Path Problem with Edge Information Reuse is NP-Complete Jesper Larsson Tr¨aff TU Wien Faculty of Informatics, Institute of Information Systems Research Group Parallel Computing Favoritenstrasse 16/184-5, 1040 Vienna, Austria email: [email protected] 15.9.2015, Revised 6.6.2016 Abstract We show that the following variation of the single-source shortest path problem is NP- complete. Let a weighted, directed, acyclic graph G = (V,E,w) with source and sink vertices s and t be given. Let in addition a mapping f on E be given that associates information with the edges (e.g., a pointer), such that f(e)= f(e′) means that edges e and e′ carry the same information; for such edges it is required that w(e)= w(e′). The length of a simple st path U is the sum of the weights of the edges on U but edges with f(e)= f(e′) are counted only once. The problem is to determine a shortest such st path. We call this problem the edge information reuse shortest path problem. It is NP-complete by reduction from 3SAT. 1 The Edge Information Reuse Shortest Path Problem A weighted, directed, acyclic graph G = (V, E, w) with source and sink vertices s,t ∈ V is given. Edges represent some possible substructures and a path from s to t determines how substructures are put together to form a desired superstructure. Edge weights reflect the cost of the associated substructures (e.g., memory consumption). An ordinary shortest path determines an ordered, tree-like representation of the superstructure of least cost: a single root with children given by the edges of the path.
    [Show full text]
  • 5 Directed Acyclic Graphs
    5 Directed acyclic graphs (5.1) Introduction In many statistical studies we have prior knowledge about a temporal or causal ordering of the variables. In this chapter we will use directed graphs to incorporate such knowledge into a graphical model for the variables. Let XV = (Xv)v∈V be a vector of real-valued random variables with probability distribution P and density p. Then the density p can always be decomposed into a product of conditional densities, d Q p(x) = p(xd|x1, . , xd−1)p(x1, . , xd−1) = ... = p(xv|x1, . , xv−1). (5.1) v=1 Note that this can be achieved for any ordering of the variables. Now suppose that the conditional density of some variable Xv does not depend on all its predecessors, namely X1,...,Xv−1, but only on a subset XUv , that is, Xv is conditionally inde- pendent of its predecessors given XUv . Substituting p(xv|xUv ) for p(xv|x1, . , xv−1) in the product (5.1), we obtain d Q p(x) = p(xv|xUv ). (5.2) v=1 This recursive dependence structure can be represented by a directed graph G by drawing an arrow from each vertex in Uv to v. As an immediate consequence of the recursive factorization, the resulting graph is acyclic, that is, it does not contain any loops. On the other hand, P factorizes with respect to the undirected graph Gm which is given by the class of complete subsets D = {{v} ∪ Uv|v ∈ V }. This graph can be obtained from the directed graph G by completing all sets {v} ∪ Uv and then converting all directed edges into undirected ones.
    [Show full text]
  • Single-Source Shortest Paths (Ch
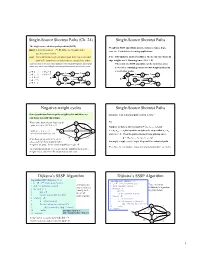
    Single-Source Shortest Paths (Ch. 24) Single-Source Shortest Paths The single-source shortest path problem (SSSP) Weights in SSSP algorithms include distances, times, hops, input: a directed graph G = (V, E) with edge weights, and a cost, etc. Used in lots of routing applications. specific source node s. goal: find a minimum weight (shortest) path from s to every other Note: BFS finds the shortest paths for the special case when all node in V (sometimes we only want the cost of these paths) edge weights are 1. Running time = O(V + E) It turns out that, in the worst case, finding the shortest path between s and a single The result of a SSSP algorithm can be viewed as a tree node t is no easier than finding the shortest paths between s and all other nodes rooted at s, containing a shortest (wrt weight) path from s à g = ¥ s to all other nodes. s à b = 2 2 3 s à c = 5 s à h = 7 a b c 2 3 5 6 a b 6 c s à d = 6 S 5 3 d 1 e S 3 s à e = 5 2 d 1 e 2 s à f = 3 f 4 g 2 h f 4 g 2 h 2 Negative-weight cycles Single-Source Shortest Paths Some graphs may have negative-weight cycles and these are Question: Can a shortest path contain a cycle? a problem for SSSP algorithms. What is the shortest path from a to d? No. b 9 · path a-c-e-d = -12+3-2 = -11 2 8 6 Suppose we have a shortest path p = áv0, v1, ..., vkñ and S -12 3 c = áv , v , ..., v ñ is a positive-weight cycle on p so that v = v · path a-c-e-d-a-c-e-d = a c e i i+1 j i j -12+3-2+(10-12+3-2)= -13 6 4 and w(c) > 0.
    [Show full text]
  • Fundamental Graph Algorithms Part II
    Fundamental Graph Algorithms Part II Outline for Today ● Dijkstra's Algorithm ● An algorithm for finding shortest paths in more realistic settings ● Depth-First Search ● A different graph search algorithm. ● Directed Acyclic Graphs ● Graphs for representing prerequisites. ● (ITA) Topological Sorting ● Algorithms for ordering dependencies. Recap from Last Time Breadth-First Search ● Given an arbitrary graph G = (V, E) and a starting node s ∈ V, breadth-first search finds shortest paths from s to each reachable node v. ● When implemented using an adjacency list, runs in O(m + n) time, which we defined to be linear time on a graph. ● One correctness proof worked in terms of “layers:” the algorithm finds all nodes at distance 0, 1, 2, … in order. A Second Intuition for BFS A Second Intuition ● At each point in the execution of BFS, a node v is either ● green, and we have the shortest path to v; ● yellow, and it is connected to some green node; or ● gray, and v is undiscovered. ● Each iteration, we pick a yellow node with minimal distance from the start node and color it green. So what is the cost of the lowest-cost yellow node? ● If v is yellow, it is connected to a green node u by an edge. ● The cost of getting from s to v is then d(s, u) + 1. ● BFS works by picking the yellow node v minimizing d(s, u) + 1 where (u, v) is an edge and u is green. Pick yellow node v minimizing d(s, u) + 1, where (u, v) is an edge and u is green.
    [Show full text]