DOCSLIB.ORG

The Shape of Congruence Lattices Keith A. Kearnes Emil W. Kiss

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Shape of Congruence Lattices Keith A. Kearnes Emil W. Kiss The Shape of Congruence Lattices Keith A. Kearnes Emil W. Kiss Author address: Department of Mathematics, University of Colorado, Boulder, CO 80309-0395, USA E-mail address: [email protected] URL: http://spot.colorado.edu/~kearnes (Emil W. Kiss) Lorand´ Eotv¨ os¨ University, Department of Algebra and Number Theory, 1117 Budapest, Pazm´ any´ Peter´ set´ any´ 1/c, Hungary E-mail address: [email protected] URL: http://www.cs.elte.hu/~ewkiss Dedicated to Bjarni J´onsson, For his work on congruence varieties, To Ralph McKenzie, For his work on commutator theories, And to Walter Taylor, For his work on Maltsev conditions. Contents Chapter 1. Introduction 1 1.1. Shapes of Congruence Lattices 1 1.2. Maltsev Conditions 3 1.3. Commutator Theories 6 1.4. The Results of This Monograph 11 Chapter 2. Preliminary Notions 15 2.1. Algebras, Varieties, and Clones 15 2.2. Lattice Theory 17 2.3. Meet Continuous Lattice Theory 22 2.4. Maltsev Conditions 23 2.5. The Term Condition 27 2.6. Congruence Identities 31 Chapter 3. Strong Term Conditions 37 3.1. Varieties Omitting Strongly Abelian Congruences 37 3.2. Join Terms 50 3.3. Abelian Tolerances and Congruences 58 Chapter 4. Meet Continuous Congruence Identities 63 4.1. Maltsev Conditions From Congruence Identities 65 4.2. Congruence Identities From Maltsev Conditions 73 4.3. Omitted Sublattices 83 4.4. Admitted Sublattices 85 Chapter 5. Rectangulation 91 5.1. Rectangular Tolerances 91 5.2. Rectangular Tolerances and Join Terms 99 5.3. Varieties Omitting Rectangular Tolerances 107 Chapter 6. A Theory of Solvability 121 6.1. Varieties With A Weak Difference Term 122 6.2. 1-Solvability 126 6.3. An Alternative Development 146 Chapter 7. Ordinary Congruence Identities 151 vii viii CONTENTS 7.1. A Rank for Solvability Obstructions 151 7.2. Congruence Identities 163 Chapter 8. Congruence Meet and Join Semidistributivity 167 8.1. Congruence Meet Semidistributivity 167 8.2. More on Congruence Identities 171 8.3. Congruence Join Semidistributivity 185 Chapter 9. Residually Small Varieties 191 9.1. Residual Smallness and Congruence Modularity 191 9.2. Almost Congruence Distributive Varieties 195 Problems 199 Bibliography 205 Index 209 Abstract We develop the theories of the strong commutator, the rectangular commutator, the strong rectangular commutator, as well as a solvabil- ity theory for the nonmodular TC commutator. These theories are used to show that each of the following sets of statements are equivalent for a variety V of algebras. (I) (a) V satisfies a nontrivial congruence identity. (b) V satisfies an idempotent Maltsev condition that fails in the variety of semilattices. (c) The rectangular commutator is trivial throughout V. (II) (a) V satisfies a nontrivial meet continuous congruence iden- tity. (b) V satisfies an idempotent Maltsev condition that fails in the variety of sets. (c) The strong commutator is trivial throughout V. (d) The strong rectangular commutator is trivial through- out V. (III) (a) V is congruence semidistributive. (b) V satisfies an idempotent Maltsev condition that fails in the variety of semilattices and in any nontrivial variety of modules. (c) The rectangular and TC commutators are both trivial throughout V. We prove that a residually small variety that satisfies a congruence identity is congruence modular. 1991 Mathematics Subject Classification. Primary 08B05; Secondary 08B10. Key words and phrases. Abelian, almost congruence distributivity, commutator theory, compatible semilattice operation, congruence identity, congruence modular- ity, congruence semidistributivity, Maltsev condition, meet continuous lattice, rect- angulation, residual smallness, solvable, tame congruence theory, term condition, variety, weak difference term. The first author was supported in part by NSF Grant #9802922. The second author was supported in part by OTKA Grants #T043671 and #T043034. ix CHAPTER 1 Introduction This monograph is concerned with the relationships between Mal- tsev conditions, commutator theories and the shapes of congruence lattices in varieties of algebras. 1.1. Shapes of Congruence Lattices Carl F. Gauss, in [23], introduced the notation (1.1) a ≡ b (mod m); which is read as \a is congruent to b modulo m", to mean that the integers a and b have the same remainder upon division by the integer modulus m, equivalently that a − b 2 mZ. As the notation suggests, congruence modulo m is an equivalence relation on Z. It develops that congruence modulo m is compatible with the ring operations of Z, and that the only equivalence relations on Z that are compatible with the ring operations are congruences modulo m for m 2 Z. Richard Dedekind conceived of a more general notion of \integer", which nowadays we call an ideal in a number ring. Dedekind extended the notation (1.1) to (1.2) a ≡ b (mod µ) where a; b 2 C and µ ⊆ C; (1.2) is defined to hold if a − b 2 µ. Dedekind called a subset µ ⊆ C a module if it could serve as the modulus of a congruence, i.e., if this relation of congruence modulo µ is an equivalence relation on C. This happens precisely when µ is closed under subtraction. For Dedekind, therefore, a \module" was an additive subgroup of C. The set of Dedekind's modules is closed under the operations of in- tersection and sum. These two operations make the set of modules into a lattice. Dedekind proposed and investigated the problem of determin- ing the identities of this lattice (the \laws of congruence arithmetic"). In 1900, in [13], he published the discovery that if α; β; γ ⊆ C are modules, then (1.3) α \ β + (α \ γ) = (α \ β) + (α \ γ): 1 2 1. INTRODUCTION This 3-variable law of the lattice of modules is now called the modular law. Dedekind went on to prove that any equational law of congru- ence arithmetic that can be expressed with at most 3 variables is a consequence of the modular law and the laws valid in all lattices. Dedekind did not write the law in the form (1.3), which is an iden- tity, but rather as a quasi-identity: for all modules α; β; γ ⊆ C (1.4) α ⊇ γ −! α \ (β + γ) = (α \ β) + γ:1 Dedekind also discovered a useful \omitting sublattices" version of the modular law. It is the assertion that there do not exist modules α; β; γ ⊆ C which generate a sublattice isomorphic to N5 (Theorem I.7.12 of [1]). β + α = β + γ @ r @ @ α β r J γ r J J r J β \ α =r β \ γ Figure 1.1. The lattice N5 More generally, a congruence on an arbitrary algebra A is an equivalence relation on the universe of A that is compatible with the operations of A. Equivalently, it is the kernel of a homomorphism with domain A. The set of all congruences is a sublattice of the lattice of equivalence relations on A.A congruence identity of A is an identity that holds in the lattice Con(A) of all congruences of A. Dedekind's observation is that the modular law is a congruence identity satisfied by C as an abelian group. In fact, it is a congruence identity of any group, ring, vector space, Boolean algebra or lattice. Dedekind's result initiated many lines of research in the 20th cen- tury, but to avoid losing focus we mention only a few. Garrett Birkhoff observed that the congruences of any group permute, meaning that α ◦β = β ◦α, and that any lattice of permuting equivalence relations is modular. This \explains" Dedekind's result to some degree, but in [22] N. Funayama and T. Nakayama showed that the lattice of congruences of a lattice satisfies the distributive law: for all α, β, γ (1.5) α \ (β + γ) = (α \ β) + (α \ γ); 1In fact, Dedekind used the symbols + and − instead of + and \. 1.2. MALTSEV CONDITIONS 3 which is stronger than the modular law, yet congruences of lattices need not permute. Thus permutability implies modularity, but not vice versa. Bjarni J´onssonthen refined the results of Birkhoff and Dedekind by showing in [37] that any lattice of permuting equivalence relations satisfies the arguesian law, which is stronger than the modular law. Conversely, he showed that any complemented lattice satisfying the arguesian law is embeddable into the lattice of congruences of an abelian group. Here the arguesian law is the 6-variable law asserting that for all αi, βi, i = 0; 1; 2, (1.6) (α0 +β0)\(α1 +β1)\(α2 +β2) ≤ α0 \(γ +α1) + β0 \(γ +β1) where γ = (α0 +α1)\(β0 +β1)\(δ0 +δ1), δ0 = (α0 +α2)\(β0 +β2) and δ1 = (α1 + α2) \ (β1 + β2). Thus J´onssonsolved the special instance of Dedekind's problem (of determining the laws of modules) which concerns only complemented lattices of modules. The full problem is still open, although in the same paper J´onssongave an example of a finite noncomplemented arguesian lattice that is not embeddable in the congruence lattice of a group, and in [30] Mark Haiman proved that lattices of permuting equivalence relations satisfy laws stronger than the arguesian law. 1.2. Maltsev Conditions Let R be the variety of rings and A be the variety of abelian groups. The fact that rings have a term-definable underlying abelian group structure may be denoted A ≤ R, i.e., rings have the structure of abelian groups and more. A. I. Maltsev proved in [63] that a variety V of algebras has the property that the congruence lattices of its members consist of permuting equivalence relations if and only if P ≤ V where P is the variety with one ternary basic operation symbol p that is axiomatized by the Maltsev identities: (1.7) p(x; y; y) ≈ x and p(y; y; x) ≈ x: In other words, V consists of congruence permutable algebras if and only if there is a ternary V-term p, called a Maltsev term, such that the identities (1.7) hold in V.
Load more

Recommended publications
  • On Some Equational Classes of Distributive Double P-Algebras
    iJEMONSTRATTO MATHEMATICA Vol IX No4 1976 Anna Romanowska ON SOME EQUATIONAL CLASSES OF DISTRIBUTIVE DOUBLE P-ALGEBRAS 1. Introduction Recently, T. Katrinak [5] showed that the two, three and four element chains are the only subdirect irreducible double Stone algebras and the lattice of equational subclasses of the equational class of all double Stone algebras forms a four element chain. R. Beazer [1] characterized the simple distri- butive double p-algebras. This paper is concerned with some other subdirectly irreducible distributive double p-algebras and with equational classes generated by these algebras. As corollary, the lattice of some equational classes of regular distributive double p-algebras is presented. 2. Preliminaries A universal algebra < L; V, A,*, 0, 1 > of type <2, 2, 1, 0, is called a p-algebra iff <L; V , A , 0, 1 > is a bounded lattice such that for every a £ L the element a*e I jL is the pseudocomplement of a, i.e. x ^ a iff a A x = 0. A universal algebra <L; V,A,*, +, 0, 1> is called a dp-al- gebra (double p-algebra) iff V, A,*, 0, 1 > is a p-alge- bra ana <Cl; V, A, 0, 1 > is a dual p-algebra (x > a+iff x V a = 1). A distributive dp-algebra is called a ddp-algebra. A distributive p-algebra (dual p-algebra) is called a Fn~algebra (F^-algebra) iff L satisfies the identity (xyV.. .AxQ)*V (X*AX2A. .AXq)*V. .. V(x1 A ... Ax*)* = 1 (P*) + + ((x1V.. .Vxk) A(x^Vx2V. ..Vxk) A. ..A(x1 V..
    [Show full text]
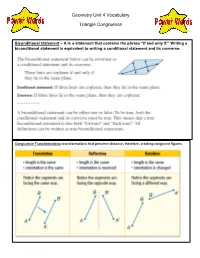
  • Geometry Unit 4 Vocabulary Triangle Congruence
    Geometry Unit 4 Vocabulary Triangle Congruence Biconditional statement – A is a statement that contains the phrase “if and only if.” Writing a biconditional statement is equivalent to writing a conditional statement and its converse. Congruence Transformations–transformations that preserve distance, therefore, creating congruent figures Congruence – the same shape and the same size Corresponding Parts of Congruent Triangles are Congruent CPCTC – the angle made by two lines with a common vertex. (When two lines meet at a common point Included angle (vertex) the angle between them is called the included angle. The two lines define the angle.) Included side – the common side of two legs. (Usually found in triangles and other polygons, the included side is the one that links two angles together. Think of it as being “included” between 2 angles. Overlapping triangles – triangles lying on top of one another sharing some but not all sides. Theorems AAS Congruence Theorem – Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangles. ASA Congruence Theorem -Triangles are congruent if any two angles and their included side are equal in both triangles. SAS Congruence Theorem -Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles. SAS SSS Congruence Theorem -Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. Special congruence theorem for RIGHT TRIANGLES! .
    [Show full text]
  • A Congruence Problem for Polyhedra
    A congruence problem for polyhedra Alexander Borisov, Mark Dickinson, Stuart Hastings April 18, 2007 Abstract It is well known that to determine a triangle up to congruence requires 3 measurements: three sides, two sides and the included angle, or one side and two angles. We consider various generalizations of this fact to two and three dimensions. In particular we consider the following question: given a convex polyhedron P , how many measurements are required to determine P up to congruence? We show that in general the answer is that the number of measurements required is equal to the number of edges of the polyhedron. However, for many polyhedra fewer measurements suffice; in the case of the cube we show that nine carefully chosen measurements are enough. We also prove a number of analogous results for planar polygons. In particular we describe a variety of quadrilaterals, including all rhombi and all rectangles, that can be determined up to congruence with only four measurements, and we prove the existence of n-gons requiring only n measurements. Finally, we show that one cannot do better: for any ordered set of n distinct points in the plane one needs at least n measurements to determine this set up to congruence. An appendix by David Allwright shows that the set of twelve face-diagonals of the cube fails to determine the cube up to conjugacy. Allwright gives a classification of all hexahedra with all face- diagonals of equal length. 1 Introduction We discuss a class of problems about the congruence or similarity of three dimensional polyhedra.
    [Show full text]
  • Semimodular Lattices Theory and Applications
    P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 ENCYCLOPEDIA OF MATHEMATICS AND ITS APPLICATIONS Semimodular Lattices Theory and Applications MANFRED STERN P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 PUBLISHED BY THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE The Pitt Building, Trumpington Street, Cambridge, United Kingdom CAMBRIDGE UNIVERSITY PRESS The Edinburgh Building, Cambridge CB2 2RU, UK http://www.cup.cam.ac.uk 40 West 20th Street, New York, NY 10011-4211, USA http://www.cup.org 10 Stamford Road, Oakleigh, Melbourne 3166, Australia c Cambridge University Press 1999 This book is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published 1999 Printed in the United States of America Typeset in 10/13 Times Roman in LATEX2ε[TB] A catalog record for this book is available from the British Library. Library of Congress Cataloging-in-Publication Data Stern, Manfred. Semimodular lattices: theory and applications. / Manfred Stern. p. cm. – (Encyclopedia of mathematics and its applications ; v. 73) Includes bibliographical references and index. I. Title. II. Series. QA171.5.S743 1999 511.303 – dc21 98-44873 CIP ISBN 0 521 46105 7 hardback P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 Contents Preface page ix 1 From Boolean Algebras to Semimodular Lattices 1 1.1 Sources of Semimodularity
    [Show full text]
  • Understand the Principles and Properties of Axiomatic (Synthetic
    Michael Bonomi Understand the principles and properties of axiomatic (synthetic) geometries (0016) Euclidean Geometry: To understand this part of the CST I decided to start off with the geometry we know the most and that is Euclidean: − Euclidean geometry is a geometry that is based on axioms and postulates − Axioms are accepted assumptions without proofs − In Euclidean geometry there are 5 axioms which the rest of geometry is based on − Everybody had no problems with them except for the 5 axiom the parallel postulate − This axiom was that there is only one unique line through a point that is parallel to another line − Most of the geometry can be proven without the parallel postulate − If you do not assume this postulate, then you can only prove that the angle measurements of right triangle are ≤ 180° Hyperbolic Geometry: − We will look at the Poincare model − This model consists of points on the interior of a circle with a radius of one − The lines consist of arcs and intersect our circle at 90° − Angles are defined by angles between the tangent lines drawn between the curves at the point of intersection − If two lines do not intersect within the circle, then they are parallel − Two points on a line in hyperbolic geometry is a line segment − The angle measure of a triangle in hyperbolic geometry < 180° Projective Geometry: − This is the geometry that deals with projecting images from one plane to another this can be like projecting a shadow − This picture shows the basics of Projective geometry − The geometry does not preserve length
    [Show full text]
  • On Generalized Topological Molecular Lattices 1. Introduction And
    Sahand Communications in Mathematical Analysis (SCMA) Vol. 10 No. 1 (2018), 1-15 http://scma.maragheh.ac.ir DOI: 10.22130/scma.2017.27148 On generalized topological molecular lattices Narges Nazari1 and Ghasem Mirhosseinkhani2∗ Abstract. In this paper, we introduce the concept of the gener- alized topological molecular lattices as a generalization of Wang's topological molecular lattices, topological spaces, fuzzy topologi- cal spaces, L-fuzzy topological spaces and soft topological spaces. Topological molecular lattices were defined by closed elements, but in this new structure we present the concept of the open elements and define a closed element by the pseudocomplement of an open element. We have two structures on a completely distributive com- plete lattice, topology and generalized co-topology which are not dual to each other. We study the basic concepts, in particular sep- aration axioms and some relations among them. 1. Introduction and preliminaries Since the set of open sets of a topological space is a frame, many important properties to topological spaces may be expressed without referring to the points. The first person who exploit possibility of ap- plying the lattice theory to the topology was Henry Wallman. He used the lattice-theoretic ideas to construct what is now called the \Wallman compactification” of a T1-topological space. This idea was pursued by Mckinsey, Tarski, N¨obeling, Lesier, Ehresmann, B´enabou, etc. How- ever, the importance of attention to open sets as a lattice appeared as late as 1962 in [3, 9]. After that, many authors became interested and developed the field. The pioneering paper [6] by Isbell merits particu- lar mention for opening several important topics.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • Dualities for Some De Morgan Algebras with Operators and Lukasiewicz Algebras
    /. Austral. Math. Soc. (Series A) 34 (1983), 377-393 DUALITIES FOR SOME DE MORGAN ALGEBRAS WITH OPERATORS AND LUKASIEWICZ ALGEBRAS ROBERTO CIGNOLI and MARTA S. DE GALLEGO (Received 3 September 1981, Revised 22 June 1982) Communicated by J. B. Miller Abstract Algebras (A, V, A, ~ , Y,0,1) of type (2,2,1,1,0,0) such that (A, V, A, ~ ,0,1) is a De Morgan algebra and y is a lattice homomorphism from A into its center that satisfies one of the conditions (i) a « ya or (ii) a < ~ a V ya are considered. The dual categories and the lattice of their subvarieties are determined, and applications to Lukasiewicz algebras are given. 1980 Mathematics subject classification (Amer. Math. Soc): 06 D 30, 03 G 20, 03 G 25, 08 B 15. Introduction Throughout this paper, A will denote the class of De Morgan algebras and 6E the category of De Morgan algebras and homomorphisms. The class of Kleene algebras (that is De Morgan algebras which satisfy the equation (aA~a)V(6 V~fe) = feV~£>) will be denoted by K, and the corresponding category by %. For each A in A, B(A) will denote the center of A, that is the subalgebra of all complemented elements of A, and K(A) the subalgebra of B(A) formed by the elements a such that the De Morgan negation ~ a coincides with the complement of a (see Cignoli and de Gallego (1981)). Let A e A. For each a G A, define Ka - {k G K(A): a < k) and Ha - {k G K(A): a =£~ a V k}.
    [Show full text]
  • Foundations of Geometry
    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2008 Foundations of geometry Lawrence Michael Clarke Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Geometry and Topology Commons Recommended Citation Clarke, Lawrence Michael, "Foundations of geometry" (2008). Theses Digitization Project. 3419. https://scholarworks.lib.csusb.edu/etd-project/3419 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Mathematics by Lawrence Michael Clarke March 2008 Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino by Lawrence Michael Clarke March 2008 Approved by: 3)?/08 Murran, Committee Chair Date _ ommi^yee Member Susan Addington, Committee Member 1 Peter Williams, Chair, Department of Mathematics Department of Mathematics iii Abstract In this paper, a brief introduction to the history, and development, of Euclidean Geometry will be followed by a biographical background of David Hilbert, highlighting significant events in his educational and professional life. In an attempt to add rigor to the presentation of Geometry, Hilbert defined concepts and presented five groups of axioms that were mutually independent yet compatible, including introducing axioms of congruence in order to present displacement.
    [Show full text]
  • Groups with Almost Modular Subgroup Lattice Provided by Elsevier - Publisher Connector
    Journal of Algebra 243, 738᎐764Ž. 2001 doi:10.1006rjabr.2001.8886, available online at http:rrwww.idealibrary.com on View metadata, citation and similar papers at core.ac.uk brought to you by CORE Groups with Almost Modular Subgroup Lattice provided by Elsevier - Publisher Connector Francesco de Giovanni and Carmela Musella Dipartimento di Matematica e Applicazioni, Uni¨ersita` di Napoli ‘‘Federico II’’, Complesso Uni¨ersitario Monte S. Angelo, Via Cintia, I 80126, Naples, Italy and Yaroslav P. Sysak1 Institute of Mathematics, Ukrainian National Academy of Sciences, ¨ul. Tereshchenki¨ska 3, 01601 Kie¨, Ukraine Communicated by Gernot Stroth Received November 14, 2000 DEDICATED TO BERNHARD AMBERG ON THE OCCASION OF HIS 60TH BIRTHDAY 1. INTRODUCTION A subgroup of a group G is called modular if it is a modular element of the lattice ᑦŽ.G of all subgroups of G. It is clear that everynormal subgroup of a group is modular, but arbitrarymodular subgroups need not be normal; thus modularitymaybe considered as a lattice generalization of normality. Lattices with modular elements are also called modular. Abelian groups and the so-called Tarski groupsŽ i.e., infinite groups all of whose proper nontrivial subgroups have prime order. are obvious examples of groups whose subgroup lattices are modular. The structure of groups with modular subgroup lattice has been described completelybyIwasawa wx4, 5 and Schmidt wx 13 . For a detailed account of results concerning modular subgroups of groups, we refer the reader towx 14 . 1 This work was done while the third author was visiting the Department of Mathematics of the Universityof Napoli ‘‘Federico II.’’ He thanks the G.N.S.A.G.A.
    [Show full text]
  • Meet Representations in Upper Continuous Modular Lattices James Elton Delany Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1966 Meet representations in upper continuous modular lattices James Elton Delany Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Mathematics Commons Recommended Citation Delany, James Elton, "Meet representations in upper continuous modular lattices " (1966). Retrospective Theses and Dissertations. 2894. https://lib.dr.iastate.edu/rtd/2894 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. This dissertation has been microiihned exactly as received 66-10,417 DE LA NY, James Elton, 1941— MEET REPRESENTATIONS IN UPPER CONTINU­ OUS MODULAR LATTICES. Iowa State University of Science and Technology Ph.D., 1966 Mathematics University Microfilms, Inc.. Ann Arbor, Michigan MEET REPRESENTATIONS IN UPPER CONTINUOUS MODULAR LATTICES by James Elton Delany A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Mathematics Approved: Signature was redacted for privacy. I _ , r Work Signature was redacted for privacy. Signature was redacted for privacy. Iowa State University of Science and Technology Ames, Iowa 1966 il TABLE OP CONTENTS Page 1. INTRODUCTION 1 2. TORSION ELEMENTS, TORSION FREE ELEMENTS, AND COVERING CONDITIONS 4 3. ATOMIC LATTICES AND UPPER CONTINUITY 8 4. COMPLETE JOIN HOMOMORPHISMS 16 5. TWO HOMOMORPHISMS 27 6.
    [Show full text]
  • ∆ Congruence & Similarity
    www.MathEducationPage.org Henri Picciotto Triangle Congruence and Similarity A Common-Core-Compatible Approach Henri Picciotto The Common Core State Standards for Mathematics (CCSSM) include a fundamental change in the geometry program in grades 8 to 10: geometric transformations, not congruence and similarity postulates, are to constitute the logical foundation of geometry at this level. This paper proposes an approach to triangle congruence and similarity that is compatible with this new vision. Transformational Geometry and the Common Core From the CCSSM1: The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type of symmetry, and the symmetries of an object offer insight into its attributes—as when the reflective symmetry of an isosceles triangle assures that its base angles are congruent. In the approach taken here, two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other. This is the principle of superposition. For triangles, congruence means the equality of all corresponding pairs of sides and all corresponding pairs of angles. During the middle grades, through experiences drawing triangles from given conditions, students notice ways to specify enough measures in a triangle to ensure that all triangles drawn with those measures are congruent. Once these triangle congruence criteria (ASA, SAS, and SSS) are established using rigid motions, they can be used to prove theorems about triangles, quadrilaterals, and other geometric figures.
    [Show full text]