DOCSLIB.ORG

Meet Representations in Upper Continuous Modular Lattices James Elton Delany Iowa State University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Meet Representations in Upper Continuous Modular Lattices James Elton Delany Iowa State University Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1966 Meet representations in upper continuous modular lattices James Elton Delany Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Mathematics Commons Recommended Citation Delany, James Elton, "Meet representations in upper continuous modular lattices " (1966). Retrospective Theses and Dissertations. 2894. https://lib.dr.iastate.edu/rtd/2894 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. This dissertation has been microiihned exactly as received 66-10,417 DE LA NY, James Elton, 1941— MEET REPRESENTATIONS IN UPPER CONTINU­ OUS MODULAR LATTICES. Iowa State University of Science and Technology Ph.D., 1966 Mathematics University Microfilms, Inc.. Ann Arbor, Michigan MEET REPRESENTATIONS IN UPPER CONTINUOUS MODULAR LATTICES by James Elton Delany A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Mathematics Approved: Signature was redacted for privacy. I _ , r Work Signature was redacted for privacy. Signature was redacted for privacy. Iowa State University of Science and Technology Ames, Iowa 1966 il TABLE OP CONTENTS Page 1. INTRODUCTION 1 2. TORSION ELEMENTS, TORSION FREE ELEMENTS, AND COVERING CONDITIONS 4 3. ATOMIC LATTICES AND UPPER CONTINUITY 8 4. COMPLETE JOIN HOMOMORPHISMS 16 5. TWO HOMOMORPHISMS 27 6. MEET IRREDUCIBLE ELEMENTS 36 7. IRREDUNDANT REPRESENTATIONS 41 8. APPLICATIONS 51 9. BIBLIOGRAPHY 58 10. ACKNOWLEDGMENTS 59 1 1. INTRODUCTION The study of representations of elements of the lattice of congruence relations of an algebra as intersections of other elements of this lattice is of interest for two reasons. In the first place, such a study offers an extension of the classical representation theory for the ideals of a noetherian ring. Secondly, there is a natural correspondence between the subdirect product representations of an algebra and the meet representations of the zero element of its lattice of con­ gruence relations. The lattice of congruence relations of any algebra is compactly generated. (An element x of a lattice is compact if whenever x 4US there is a finite set FcS such that x^ijF, A complete lattice is said to be compactly generated if each element is the union of a set of compact elements.) In order to study the subdirect product representations of an algebra it often suffices to investigate meet representations in compactly generated lattices. For example, the fact that any algebra has a subdirect product representation in terms of subdirectly irreducible factor algebras may be regarded as a consequence of the fact that each element of a compactly generated lattice has a meet representation in terms of com- I pletely meet irreducible elements. (An element x of a lattice is meet irreducible if xssj^o Sg implies that either x=s^ or xaSg. It is completely meet irreducible if x=Os implies X g S.) A meet representation of an element, say x=S, is 2 irredundant if x<fl(S - s) for each seS, Although any ele­ ment of a compactly generated lattice has meet representations in terms of completely meet irreducible elements, it is not true that it must possess an irredundant one. For example, Dilworth and Crawley have characterized the compactly generated modular lattices in which each element has such a representa­ tion as those which are atomic (2). (A lattice is atomic if whenever x<y there exists x' such that x-<x'^. Here, as throughout this paper, x -<x' signifies that x is covered by x'.) Our goal is to find compactly generated modular lattices in which each element has an irredundant representation in terms of meet irreducible elements (instead of completely meet irreducible elements.) Actually, for our purposes it will suffice to consider upper continuous modular lattices. (A complete lattice is upper continuous if for each element X and each chain of elements S the relation x A Us=(Jg (xn s) holds.) Any compactly generated lattice is upper continuous. On one hand we will see that there is an analogy between the case dealing with meet irreducible elements and that in­ volving completely meet irreducible elements. This may be seen by comparing Theorem 7.4 to Theorem 7.5, the latter being a restatement of the above mentioned result of Dilworth and Crawley. In a somewhat different vein we will show that a cer­ tain type of lattice homomorphism is useful in studying ir­ redundant representations and the role played by covers in such representations. Adopting the terminology used in (3) 3 we say that a lattice homomorphism .<|>:L-+-L* is a complete join homomorphism if L and L' are complete and for each Sc=L we have *(U S)= U S € o (s). Our principal results concerning such maps are the following. If L is an upper continuous modular lattice then there is an associated upper continuous modular lattice L* which is the "largest" homomorphic image of L (under a complete join epimorphism) possessing no covers. (See Theorem 5.3) Each element of L has an irredundant repre­ sentation in teirms of meet irreducibles if and only if each element of L* has such a representation. In particular, if L* consists of one element then each element of L has an irredundant representation in terms of meet irreducible ele^ ments. The class of upper continuous modular lattices for which L* consists of one element is large enough to include both the atomic ones, in which each element has an irredun­ dant representation in terms of completely meet irreducible elements, and those satisfying the ascending chain condition, in which each element has an irredundant representation as the meet of a finite number of meet irreducible elements. 4 2. TORSION ELEMENTS, TORSION FREE ELEMENTS, AND COVERING CONDITIONS We begin by generalizing two concepts from group theory. Definition. An element t of a lattice L is a torsion element if for each a<t there is a b in L such that t^>-a. The element 0 is always a torsion element. If 1 is a torsion element, we will call L a torsion lattice. Definition. An element of L is torsion free if no element of L covers it. Here 1 is always torsion free. Let H be a subgroup of an abelian group G, and let L(G) denote the lattice of subgroups of G. H is a torsion element of L(G) if and only if H is a torsion group. H is torsion free in L(G) if and only if G/H is a torsion free group. In fact the duals of the above definitions have counterparts in the theory of abelian groups. H is dual torsion free in L(G) if and only if H is a divisible group. H is a dual torsion element of L(G) if and only if G/H is a reduced group. In general it is not the case that a lattice must possess maximal torsion elements or minimal torsion free elements. Examples are easily constructed by violating the following condition. Definition. A lattice satisfies the lower covering condition if a>-a n b implies au b>-bl The dual of this condition is termed the upper covering 5 condition. If a and b are elements of a modular lattice then the intervals [an b,a] and [b,au b] are isomorphic. Thus a modular lattice satisfies both covering conditions. Our first theorem is a direct generalization of a clas­ sical theorem of group theory. Theorem 2.1 In a complete lattice which satisfies the lower covering condition there is an element which is both the largest torsion element and the smallest torsion free element. Before proving this we will develop some lemmas. In the remainder of this section it is assumed that the lattice under discussion is complete and satisfies the lower covering condition. Lemma 2.1 If x is a torsion element of "L, , and [y, z] has no atoms, then y^. Proof. Assume x n y<x. Since x is a torsion element there is a c such that x^c>-xn y. Now xny^cny^c so that either c n y=c or cny-xny. If c n y=c we would have c=c n x^ n X -<c. Hence c n y=x n y so that c>- c n y. By the lower covering condition, cvy>-y. But cuy^uy^z, contrary to the hypothesis that [y,z] has no atoms. Thus xn y=x and y>f. Lemma 2.1 has the following three consequences. Lemma 2.2 If x is a torsion element and y is torsion free then x^. Proof: Let z«l. Then x,y, and z satisfy the hypo­ 6 thesis of Lemma 2.1. Lemma 2.3. If T is a collection of torsion elements then U T is a torsion element. Proof; Suppose y^UT and [y/UT] has no atoms. If tfiT, t;^L/T and Lemma 2.1 implies y^t. Then y^UT. Hence y=UT and UT is a torsion element. Lemma 2.4. If t is a torsion element of L and t'>-t then t' is also a torsion element. Proof; Suppose y^t' and [y,t'] has no atoms. By Lemma 2.1, y^t. But y^t since t't. Hence y=t' and t' is a torsion element.
Load more

Recommended publications
  • Semimodular Lattices Theory and Applications
    P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 ENCYCLOPEDIA OF MATHEMATICS AND ITS APPLICATIONS Semimodular Lattices Theory and Applications MANFRED STERN P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 PUBLISHED BY THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE The Pitt Building, Trumpington Street, Cambridge, United Kingdom CAMBRIDGE UNIVERSITY PRESS The Edinburgh Building, Cambridge CB2 2RU, UK http://www.cup.cam.ac.uk 40 West 20th Street, New York, NY 10011-4211, USA http://www.cup.org 10 Stamford Road, Oakleigh, Melbourne 3166, Australia c Cambridge University Press 1999 This book is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published 1999 Printed in the United States of America Typeset in 10/13 Times Roman in LATEX2ε[TB] A catalog record for this book is available from the British Library. Library of Congress Cataloging-in-Publication Data Stern, Manfred. Semimodular lattices: theory and applications. / Manfred Stern. p. cm. – (Encyclopedia of mathematics and its applications ; v. 73) Includes bibliographical references and index. I. Title. II. Series. QA171.5.S743 1999 511.303 – dc21 98-44873 CIP ISBN 0 521 46105 7 hardback P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 Contents Preface page ix 1 From Boolean Algebras to Semimodular Lattices 1 1.1 Sources of Semimodularity
    [Show full text]
  • Groups with Almost Modular Subgroup Lattice Provided by Elsevier - Publisher Connector
    Journal of Algebra 243, 738᎐764Ž. 2001 doi:10.1006rjabr.2001.8886, available online at http:rrwww.idealibrary.com on View metadata, citation and similar papers at core.ac.uk brought to you by CORE Groups with Almost Modular Subgroup Lattice provided by Elsevier - Publisher Connector Francesco de Giovanni and Carmela Musella Dipartimento di Matematica e Applicazioni, Uni¨ersita` di Napoli ‘‘Federico II’’, Complesso Uni¨ersitario Monte S. Angelo, Via Cintia, I 80126, Naples, Italy and Yaroslav P. Sysak1 Institute of Mathematics, Ukrainian National Academy of Sciences, ¨ul. Tereshchenki¨ska 3, 01601 Kie¨, Ukraine Communicated by Gernot Stroth Received November 14, 2000 DEDICATED TO BERNHARD AMBERG ON THE OCCASION OF HIS 60TH BIRTHDAY 1. INTRODUCTION A subgroup of a group G is called modular if it is a modular element of the lattice ᑦŽ.G of all subgroups of G. It is clear that everynormal subgroup of a group is modular, but arbitrarymodular subgroups need not be normal; thus modularitymaybe considered as a lattice generalization of normality. Lattices with modular elements are also called modular. Abelian groups and the so-called Tarski groupsŽ i.e., infinite groups all of whose proper nontrivial subgroups have prime order. are obvious examples of groups whose subgroup lattices are modular. The structure of groups with modular subgroup lattice has been described completelybyIwasawa wx4, 5 and Schmidt wx 13 . For a detailed account of results concerning modular subgroups of groups, we refer the reader towx 14 . 1 This work was done while the third author was visiting the Department of Mathematics of the Universityof Napoli ‘‘Federico II.’’ He thanks the G.N.S.A.G.A.
    [Show full text]
  • This Is the Final Preprint Version of a Paper Which Appeared at Algebraic & Geometric Topology 17 (2017) 439-486
    This is the final preprint version of a paper which appeared at Algebraic & Geometric Topology 17 (2017) 439-486. The published version is accessible to subscribers at http://dx.doi.org/10.2140/agt.2017.17.439 SIMPLICIAL COMPLEXES WITH LATTICE STRUCTURES GEORGE M. BERGMAN Abstract. If L is a finite lattice, we show that there is a natural topological lattice structure on the geo- metric realization of its order complex ∆(L) (definition recalled below). Lattice-theoretically, the resulting object is a subdirect product of copies of L: We note properties of this construction and of some variants, and pose several questions. For M3 the 5-element nondistributive modular lattice, ∆(M3) is modular, but its underlying topological space does not admit a structure of distributive lattice, answering a question of Walter Taylor. We also describe a construction of \stitching together" a family of lattices along a common chain, and note how ∆(M3) can be regarded as an example of this construction. 1. A lattice structure on ∆(L) I came upon the construction studied here from a direction unrelated to the concept of order complex; so I will first motivate it in roughly the way I discovered it, then recall the order complex construction, which turns out to describe the topological structures of these lattices. 1.1. The construction. The motivation for this work comes from Walter Taylor's paper [20], which ex- amines questions of which topological spaces { in particular, which finite-dimensional simplicial complexes { admit various sorts of algebraic structure, including structures of lattice. An earlier version of that paper asked whether there exist spaces which admit structures of lattice, but not of distributive lattice.
    [Show full text]
  • The Variety of Modular Lattices Is Not Generated
    TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 255, November 1979 THE VARIETYOF MODULAR LATTICES IS NOT GENERATED BY ITS FINITE MEMBERS BY RALPH FREESE1 Abstract. This paper proves the result of the title. It shows that there is a five-variable lattice identity which holds in all finite modular lattices but not in all modular lattices. It is also shown that every free distributive lattice can be embedded into a free modular lattice. An example showing that modular lattice epimorphisms need not be onto is given. We prove the result of the title by constructing a simple modular lattice of length six not in the variety generated by all finite modular lattices. This lattice can be generated by five elements and thus the free modular lattice on five generators, FM (5), is not residually finite. Our lattice is constructed using the technique of Hall and Dilworth [9] and is closely related to their third example. Let F and K be countably infinite fields of characteristics p and q, where p and q are distinct primes. Let Lp be the lattice of subspaces of a four-dimensional vector space over F, Lq the lattice of subspaces of a four-dimensional vector space over K. Two-dimen- sional quotients (i.e. intervals) in both lattices are always isomorphic to Mu (the two-dimensional lattice with « atoms). Thus Lp and Lq may be glued together over a two-dimensional quotient via [9], and this is our lattice. Notice that if F and K were finite fields we could not carry out the above construction since two-dimensional quotients of Lp would have/)" + 1 atoms and those of Lq would have qm + 1, for some n, m > 1.
    [Show full text]
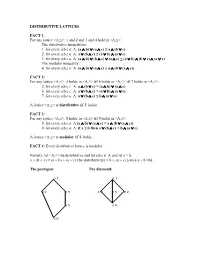
  • DISTRIBUTIVE LATTICES FACT 1: for Any Lattice <A,≤>: 1 and 2 and 3 and 4 Hold in <A,≤>: the Distributive Inequal
    DISTRIBUTIVE LATTICES FACT 1: For any lattice <A,≤>: 1 and 2 and 3 and 4 hold in <A,≤>: The distributive inequalities: 1. for every a,b,c ∈ A: (a ∧ b) ∨ (a ∧ c) ≤ a ∧ (b ∨ c) 2. for every a,b,c ∈ A: a ∨ (b ∧ c) ≤ (a ∨ b) ∧ (a ∨ c) 3. for every a,b,c ∈ A: (a ∧ b) ∨ (b ∧ c) ∨ (a ∧ c) ≤ (a ∨ b) ∧ (b ∨ c) ∧ (a ∨ c) The modular inequality: 4. for every a,b,c ∈ A: (a ∧ b) ∨ (a ∧ c) ≤ a ∧ (b ∨ (a ∧ c)) FACT 2: For any lattice <A,≤>: 5 holds in <A,≤> iff 6 holds in <A,≤> iff 7 holds in <A,≤>: 5. for every a,b,c ∈ A: a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) 6. for every a,b,c ∈ A: a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) 7. for every a,b,c ∈ A: a ∨ (b ∧ c) ≤ b ∧ (a ∨ c). A lattice <A,≤> is distributive iff 5. holds. FACT 3: For any lattice <A,≤>: 8 holds in <A,≤> iff 9 holds in <A,≤>: 8. for every a,b,c ∈ A:(a ∧ b) ∨ (a ∧ c) = a ∧ (b ∨ (a ∧ c)) 9. for every a,b,c ∈ A: if a ≤ b then a ∨ (b ∧ c) = b ∧ (a ∨ c) A lattice <A,≤> is modular iff 8. holds. FACT 4: Every distributive lattice is modular. Namely, let <A,≤> be distributive and let a,b,c ∈ A and let a ≤ b. a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) [by distributivity] = b ∧ (a ∨ c) [since a ∨ b =b]. The pentagon: The diamond: o 1 o 1 o z o y x o o y o z o x o 0 o 0 THEOREM 5: A lattice is modular iff the pentagon cannot be embedded in it.
    [Show full text]
  • Modular Lattices
    Wednesday 1/30/08 Modular Lattices Definition: A lattice L is modular if for every x; y; z 2 L with x ≤ z, (1) x _ (y ^ z) = (x _ y) ^ z: (Note: For all lattices, if x ≤ z, then x _ (y ^ z) ≤ (x _ y) ^ z.) Some basic facts and examples: 1. Every sublattice of a modular lattice is modular. Also, if L is distributive and x ≤ z 2 L, then x _ (y ^ z) = (x ^ z) _ (y ^ z) = (x _ y) ^ z; so L is modular. 2. L is modular if and only if L∗ is modular. Unlike the corresponding statement for distributivity, this is completely trivial, because the definition of modularity is invariant under dualization. 3. N5 is not modular. With the labeling below, we have a ≤ b, but a _ (c ^ b) = a _ 0^ = a; (a _ c) ^ b = 1^ ^ b = b: b c a ∼ 4. M5 = Π3 is modular. However, Π4 is not modular (exercise). Modular lattices tend to come up in algebraic settings: • Subspaces of a vector space • Subgroups of a group • R-submodules of an R-module E.g., if X; Y; Z are subspaces of a vector space V with X ⊆ Z, then the modularity condition says that X + (Y \ Z) = (X + Y ) \ Z: Proposition 1. Let L be a lattice. TFAE: 1. L is modular. 2. For all x; y; z 2 L, if x 2 [y ^ z; z], then x = (x _ y) ^ z. 2∗. For all x; y; z 2 L, if x 2 [y; y _ z], then x = (x ^ z) _ y.
    [Show full text]
  • Dimensional Functions Over Partially Ordered Sets
    Intro Dimensional functions over posets Application I Application II Dimensional functions over partially ordered sets V.N.Remeslennikov, E. Frenkel May 30, 2013 1 / 38 Intro Dimensional functions over posets Application I Application II Plan The notion of a dimensional function over a partially ordered set was introduced by V. N. Remeslennikov in 2012. Outline of the talk: Part I. Definition and fundamental results on dimensional functions, (based on the paper of V. N. Remeslennikov and A. N. Rybalov “Dimensional functions over posets”); Part II. 1st application: Definition of dimension for arbitrary algebraic systems; Part III. 2nd application: Definition of dimension for regular subsets of free groups (L. Frenkel and V. N. Remeslennikov “Dimensional functions for regular subsets of free groups”, work in progress). 2 / 38 Intro Dimensional functions over posets Application I Application II Partially ordered sets Definition A partial order is a binary relation ≤ over a set M such that ∀a ∈ M a ≤ a (reflexivity); ∀a, b ∈ M a ≤ b and b ≤ a implies a = b (antisymmetry); ∀a, b, c ∈ M a ≤ b and b ≤ c implies a ≤ c (transitivity). Definition A set M with a partial order is called a partially ordered set (poset). 3 / 38 Intro Dimensional functions over posets Application I Application II Linearly ordered abelian groups Definition A set A equipped with addition + and a linear order ≤ is called linearly ordered abelian group if 1. A, + is an abelian group; 2. A, ≤ is a linearly ordered set; 3. ∀a, b, c ∈ A a ≤ b implies a + c ≤ b + c. Definition The semigroup A+ of all nonnegative elements of A is defined by A+ = {a ∈ A | 0 ≤ a}.
    [Show full text]
  • On the Equational Theory of Projection Lattices of Finite Von Neumann
    The Journal of Symbolic Logic Volume 00, Number 0, XXX 0000 ON THE EQUATIONAL THEORY OF PROJECTION LATTICES OF FINITE VON-NEUMANN FACTORS CHRISTIAN HERRMANN Abstract. For a finite von-Neumann algebra factor M, the projections form a modular ortholattice L(M) . We show that the equational theory of L(M) coincides with that of some resp. all L(Cn×n) and is decidable. In contrast, the uniform word problem for the variety generated by all L(Cn×n) is shown to be undecidable. §1. Introduction. Projection lattices L(M) of finite von-Neumann algebra factors M are continuous orthocomplemented modular lattices and have been considered as logics resp. geometries of quantum meachnics cf. [25]. In the finite dimensional case, the correspondence between irreducible lattices and algebras, to wit the matrix rings Cn×n, has been completely clarified by Birkhoff and von Neumann [5]. Combining this with Tarski’s [27] decidability result for the reals and elementary geometry, decidability of the first order theory of L(M) for a finite dimensional factor M has been observed by Dunn, Hagge, Moss, and Wang [7]. The infinite dimensional case has been studied by von Neumann and Murray in the landmark series of papers on ‘Rings of Operators’ [23], von Neumann’s lectures on ‘Continuous Geometry’ [28], and in the treatment of traces resp. transition probabilities in a ring resp. lattice-theoretic framework [20, 29]. The key to an algebraic treatment is the coordinatization of L(M) by a ∗- regular ring U(M) derived from M and having the same projections: L(M) is isomorphic to the lattice of principal right ideals of U(M) (cf.
    [Show full text]
  • Congruence Lattices of Lattices
    App end ix C Congruence lattices of lattices G. Gratzer and E. T. Schmidt In the early sixties, wecharacterized congruence lattices of universal algebras as algebraic lattices; then our interest turned to the characterization of congruence lattices of lattices. Since these lattices are distributive, we gured that this must b e an easier job. After more then 35 years, we know that wewere wrong. In this App endix, we give a brief overview of the results and metho ds. In Section 1, we deal with nite distributive lattices; their representation as congru- ence lattices raises manyinteresting questions and needs sp ecialized techniques. In Section 2, we discuss the general case. A related topic is the lattice of complete congruences of a complete lattice. In contrast to the previous problem, we can characterize complete congruence lattices, as outlined in Section 3. 1. The Finite Case The congruence lattice, Con L, of a nite lattice L is a nite distributive lattice N. Funayama and T. Nakayama, see Theorem I I.3.11. The converse is a result of R. P. Dilworth see Theorem I I.3.17, rst published G. Gratzer and E. T. Schmidt [1962]. Note that the lattice we construct is sectionally complemented. In Section I I.1, we learned that a nite distributive lattice D is determined by the p oset J D of its join-irreducible elements, and every nite p oset can b e represented as J D , for some nite distributive lattice D . So for a nite lattice L, we can reduce the characterization problem of nite congruence lattices to the representation of nite p osets as J Con L.
    [Show full text]
  • Generating All Modular Lattices of a Given Size ADAM 2013
    Generating all modular lattices of a given size ADAM 2013 Nathan Lawless Chapman University June 6-8, 2013 Outline I Introduction to Lattice Theory: Modular Lattices I The Objective: Generating and Counting Modular Lattices I First Approach: From Finite Lattices I Second Approach: From Distributive Lattices I Results I Conclusion Then, we say a partially ordered set (L; ≤) is a lattice if it satisfies the following axioms: I For any two elements a and b of L, there exists a least upper bound, refered to as the join a _ b. I For any two elements a and b of L, there exists a greatest lower bound, refered to as the meet a ^ b. What are lattices? First, let a partially ordered set or poset be a binary relation \≤" over a set P such that 8a; b; c 2 P satisfies: I Reflexivity: a ≤ a. I Antisymmetry: if a ≤ b and b ≤ a, then a = b. I Transitivity: if a ≤ b and b ≤ c, then a ≤ c. What are lattices? First, let a partially ordered set or poset be a binary relation \≤" over a set P such that 8a; b; c 2 P satisfies: I Reflexivity: a ≤ a. I Antisymmetry: if a ≤ b and b ≤ a, then a = b. I Transitivity: if a ≤ b and b ≤ c, then a ≤ c. Then, we say a partially ordered set (L; ≤) is a lattice if it satisfies the following axioms: I For any two elements a and b of L, there exists a least upper bound, refered to as the join a _ b.
    [Show full text]
  • Supermodular Lattices
    Supermodular Lattices Iqbal Unnisa W. B. Vasantha Kandasamy Florentin Smarandache Educational Publisher Inc. Ohio 2012 This book can be ordered from: Education Publisher Inc. 1313 Chesapeake Ave. Columbus, Ohio 43212, USA Toll Free: 1-866-880-5373 Copyright 2012 by Educational Publisher Inc. and the Authors Peer reviewers: Prof. Mihàly Bencze, Department of Mathematics, Áprily Lajos College, Braşov, Romania Dr. Sebastian Nicolaescu, 2 Terrace Ave., West Orange, NJ 07052, USA. Prof. Valeri Kroumov, Okayama Univ. of Science, Okayama, Japan. Many books can be downloaded from the following Digital Library of Science: http://www.gallup.unm.edu/~smarandache/eBooks-otherformats.htm ISBN-13: 978-1-59973-195-7 EAN: 9781599731957 Printed in the United States of America 2 CONTENTS Dedication 5 Preface 7 Chapter One PRELIMINARIES 9 Chapter Two SIMPLE MODULAR LATTICES OF FINITE LENGTH 15 Chapter Three SUPERMODULAR LATTICES 31 Chapter Four SEMI SUPERMODULAR LATTICES 51 3 Chapter Five SOME INTERESTING EQUATIONAL CLASSES OF MODULAR LATTICES 75 Chapter Six SMARANDACHE LATTICES 85 Chapter Seven GB-ALGEBRAIC STRUCTURES 99 FURTHER READING 127 INDEX 129 ABOUT THE AUTHORS 131 4 DEDICATION Mr. Mohammed Jalauddin Kokan and Mrs. Aaisha Begum 5 We dedicate this book to the memory of Dr. Iqbal Unnisa's parents. Her father Mr. Mohammed Jalauddin Kokan was the Post Master in Meenambur and mother Mrs. Aaisha Begum was a housewife. From this remote village of Meenambur in Tamilnadu, her parents shifted to Chennai to educate their children. In those days, girl children being enrolled in primary school was rare. Yet, the Kokans succeeded in educating their daughters into doctors and doctorates.
    [Show full text]
  • A Geometric Description of Modular Lattices
    A Geometric Description of Modular Lattices Christian Herrmann, Douglas Pickering, and Michael Roddy October 89 1 Introduction Baer [1] observed that modular lattices of finite length (for example subgroup lattices of abelian groups) can be conceived as subspace lattices of a projective geometry structure on an ordered point set; the set of join irreducibles which in this case are the cyclic subgroups of prime power order. That modular lattices of finite length can be recaptured from the order on the points and, in addition, the incidence of points with `lines', the joins of two points, or the blocks of collinear points has been elaborated by Kurinnoi [18] , Faigle and Herrmann [7], Benson and Conway [2] , and , in the general framework of the `core' of a lattice, by Duquenne [5]. In [7] an axiomatization in terms of point-line incidence has been given. Here, we consider, more generally, modular lattices in which every element is the join of completely join irreducible `points'. We prove the isomorphy of an algebraic lattice of this kind and the associated subspace lattice and give a first order characterization of the associated `ordered spaces' in terms of collinearity and order which appears more natural and powerful. The crucial axioms are a `triangle axiom', which includes the degenerate cases, and a strengthened `line regularity axiom', both derived from [7]. As a consequence, using Skolemization, we get that any variety of modular lattices is generated by subspace latices of countable spaces. The central concept, connecting the geometric structure and the lattice structure, is that of a line interval (p + q)=(p + q) where p and q are points and p; q their unique lower covers.
    [Show full text]