DOCSLIB.ORG

Dimensional Functions Over Partially Ordered Sets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Dimensional Functions Over Partially Ordered Sets Intro Dimensional functions over posets Application I Application II Dimensional functions over partially ordered sets V.N.Remeslennikov, E. Frenkel May 30, 2013 1 / 38 Intro Dimensional functions over posets Application I Application II Plan The notion of a dimensional function over a partially ordered set was introduced by V. N. Remeslennikov in 2012. Outline of the talk: Part I. Definition and fundamental results on dimensional functions, (based on the paper of V. N. Remeslennikov and A. N. Rybalov “Dimensional functions over posets”); Part II. 1st application: Definition of dimension for arbitrary algebraic systems; Part III. 2nd application: Definition of dimension for regular subsets of free groups (L. Frenkel and V. N. Remeslennikov “Dimensional functions for regular subsets of free groups”, work in progress). 2 / 38 Intro Dimensional functions over posets Application I Application II Partially ordered sets Definition A partial order is a binary relation ≤ over a set M such that ∀a ∈ M a ≤ a (reflexivity); ∀a, b ∈ M a ≤ b and b ≤ a implies a = b (antisymmetry); ∀a, b, c ∈ M a ≤ b and b ≤ c implies a ≤ c (transitivity). Definition A set M with a partial order is called a partially ordered set (poset). 3 / 38 Intro Dimensional functions over posets Application I Application II Linearly ordered abelian groups Definition A set A equipped with addition + and a linear order ≤ is called linearly ordered abelian group if 1. A, + is an abelian group; 2. A, ≤ is a linearly ordered set; 3. ∀a, b, c ∈ A a ≤ b implies a + c ≤ b + c. Definition The semigroup A+ of all nonnegative elements of A is defined by A+ = {a ∈ A | 0 ≤ a}. 4 / 38 Intro Dimensional functions over posets Application I Application II A−dimensional functions Let M be a poset and A be a linearly ordered abelian group. Definition The function d : M → A+ is called A-dimensional over M if ∀x, y ∈ M if x < y in M, then d(x) < d(y) in A. 5 / 38 Intro Dimensional functions over posets Application I Application II Dense dimensional functions Definition An A-dimensional function d : M → A+ is called dense if for all x, y ∈ M such that d(x) < d(y) there exist elements x′ and y ′ in M satisfying d(x) ≤ d(x′), d(y ′) ≤ d(y) and x′ < y ′. 6 / 38 Intro Dimensional functions over posets Application I Application II Strongly dense dimensional functions Definition An A−dimensional function d : M → A+ is called strongly dense if for every x, y ∈ M such that d(x) < d(y) there exist elements x′, y ′ satisfying d(x)= d(x′), d(y ′)= d(y) and x′ < y ′. 7 / 38 Intro Dimensional functions over posets Application I Application II Flows The A− dimensional function d : M → A+ defines an equivalence relation ∼d on M by m1 ∼d m2 ↔ d(m1)= d(m2). Let [m1] ≤d [m2] ↔ d(m1) ≤ d(m2). Then the linearly ordered set M/ ∼d is a homomorphic image of M. Definition The set M/ ∼d is called a d−flow. The order type of a d−flow is denoted by πd (M). 8 / 38 Intro Dimensional functions over posets Application I Application II Equivalence of dimensional functions Definition Let M be a poset and suppose d1, d2 are dimensional functions over M with values in some linearly ordered abelian groups. Then d1 ∼ d2 if the order types πd1 (M) and πd2 (M) are isomorphic. Fact A poset M may have non-equivalent dimensional functions. 9 / 38 Intro Dimensional functions over posets Application I Application II Example of non-equivalent dimensional functions Example Let L1 = {[0, 1], 2, 3, [4, 5]} and L2 = {[6, 7], 8, [9, 10]}, with the natural order on them, and suppose that all elements of L1 and L2 are non-comparable. Let M = L1 ∪ L2. Then M admits non-equivalent dimensional functions. Define d1 : M → R as follows: let d1 shift all elements of L2 to the left by 1, and let it fix L1. In this case, πd1 (M)= {[0, 1], 2, 3, [4, 6], 7, [8, 9]}. Define d2 : M → R as follows: let d2 map L2 into {[−4, −3], −2, [−1, 0]}, and let it fix L1. In this case, πd2 (M)= {[−4, −3], −2, [−1, 1], 2, 3, [4, 5]}. Clearly, d1, d2 are dimensional functions, but πd1 (M) and πd2 (M) are non-isomorphic. Therefore, d1 is not equivalent to d2. 10 / 38 Intro Dimensional functions over posets Application I Application II The case of finite posets Proposition Let M be a finite poset. Then, up to the equivalence relation defined above, there exist only one Z-dimensional function over M. In particular, there exist only one strongly dense Z-dimensional function over M in this equivalence class. 11 / 38 Intro Dimensional functions over posets Application I Application II The category of posets with dimensional functions Let L be a language (or a signature) defining the category of posets with dimensional functions. Then L is the disjoint union of three languages: LM = {≤M }, where ≤M is a binary predicate; LA = {+, −, ≤A, 0}, where + is a binary predicate (addition), − is a unary predicate (inversion), and ≤A is a binary predicate of order, 0 is a constant symbol; L3 = {δM , δA, d} consists of two unary predicates that distinguish sets M and A and a binary predicate d corresponding to the graph of the dimensional function. 12 / 38 Intro Dimensional functions over posets Application I Application II The category of posets with dimensional functions We define the category K of posets with dimensional functions over L using the following 4 groups of axioms: Disjoint union of underlying sets M′ = M ⊔ A, where M is the underlying set of the predicate δM , and A is the underlying set of the predicate δA. Axioms of partial order on M. Axioms of abelian linearly ordered group A. Axioms of dimensional functions d : M → A+. 13 / 38 Intro Dimensional functions over posets Application I Application II Existence of dimensional functions Theorem 1. For every poset M there exist a linearly ordered abelian group A and a dimensional function d : M → A+. 14 / 38 Intro Dimensional functions over posets Application I Application II Discrete linearly ordered abelian groups Definition A linearly ordered abelian group A is called discrete if A+ has minimal nonzero element (denoted by 1A). Theorem If for a poset M and discrete linearly ordered group A there exists a dimensional function d : M → A+, then there exists a dense dimensional function d ∗ : M → A+. 15 / 38 Intro Dimensional functions over posets Application I Application II Dimensional functions for direct products Theorem Let di : Mi → A be a dimensional function for a poset Mi , i = 1, 2. Then the function d : M1 × M2 → A such that ∀m1 ∈ M1 ∀m2 ∈ M2 d((m1, m2)) = d1(m1)+ d2(m2), is a dimensional function for the direct product M1 × M2. 16 / 38 Intro Dimensional functions over posets Application I Application II Ordinal dimensional functions Definition An A−dimensional function on a poset M is called ordinal, if the order type πd (M) is a well ordered set. A poset M is called a set of ordinal type, if there exists a dense ordinal dimensional function for M. Definition A poset M is called Artinian if any chain a1 > a2 >... in M is finite (i.e. satisfies DCC). 17 / 38 Intro Dimensional functions over posets Application I Application II Ordinal dimensional functions Theorem 2. 1. If a poset M has an ordinal dimensional function, then it is an Artinian poset. 2. For an Artinian poset there exists a unique (up to equivalence) dense ordinal A−dimensional function. 18 / 38 Intro Dimensional functions over posets Application I Application II Lattice dimensional functions A poset L is a lattice, if 1. for any two elements x, y ∈ L, the set {a, b} has the greatest lower bound (x ∧ y), and 2. for any two elements x, y ∈ L, the set {a, b} has the least upper bound (x ∨ y). 19 / 38 Intro Dimensional functions over posets Application I Application II Lattice dimensional functions Uuniversal algebra point of view: L is an algebraic system with two binary operations ∧ and ∨ satisfying universal identities: (L1) Laws of idempotency: ∀aa ∧ a = a, a ∨ a = a. (L2) Commutativity laws: ∀a, ba ∧ b = b ∧ a, a ∨ b = b ∨ a. (L3) Associativity laws: ∀a, b, c (a ∧ b) ∧ c = a ∧ (b ∧ c), (a ∨ b) ∨ c = a ∨ (b ∨ c). (L4) Absorption laws: ∀a, b a ∧ (a ∨ b)= a, a ∨ (a ∧ b)= a. Using these operations, one can define a partial order: a ≤ b ↔ a ∧ b = a. 20 / 38 Intro Dimensional functions over posets Application I Application II Lattice dimensional functions Definition Let a poset M be a lattice, and let A be a linearly ordered abelian group. A function d : M → A+ is called a lattice A-dimensional function if 1 d is A-dimensional function. 2 ∀x, y ∈ M d(x ∨ y)+ d(x ∧ y)= d(x)+ d(y). 21 / 38 Intro Dimensional functions over posets Application I Application II Modular lattices Definition A lattice L is called modular, if ∀x∀y∀z ∈ L z ≤ x → x ∧ (y ∨ z) = (x ∧ y) ∨ z. For a modular lattice L with zero one can define a height function h : L → N: h(a) is the length of the longest maximal chain in the interval [0, a], if it exists, and h(a)= ∞, otherwise. Definition A lattice L is called a finite length lattice if h(a) < ∞ for all a ∈ L. 22 / 38 Intro Dimensional functions over posets Application I Application II Modular lattices Jordan-Goelder theorem In a finite length modular lattice every two maximal chains in [0, a] have the same length and for all a, b ∈ L the following equality holds h(a)+ h(b)= h(a ∧ b)+ h(a ∨ b).
Load more

Recommended publications
  • Order Types and Structure of Orders
    ORDER TYPES AND STRUCTURE OF ORDERS BY ANDRE GLEYZALp) 1. Introduction. This paper is concerned with operations on order types or order properties a and the construction of order types related to a. The reference throughout is to simply or linearly ordered sets, and we shall speak of a as either property or type. Let a and ß be any two order types. An order A will be said to be of type aß if it is the sum of /3-orders (orders of type ß) over an a-order; i.e., if A permits of decomposition into nonoverlapping seg- ments each of order type ß, the segments themselves forming an order of type a. We have thus associated with every pair of order types a and ß the product order type aß. The definition of product for order types automatically associates with every order type a the order types aa = a2, aa2 = a3, ■ ■ ■ . We may further- more define, for all ordinals X, a Xth power of a, a\ and finally a limit order type a1. This order type has certain interesting properties. It has closure with respect to the product operation, for the sum of ar-orders over an a7-order is an a'-order, i.e., a'al = aI. For this reason we call a1 iterative. In general, we term an order type ß having the property that ßß = ß iterative, a1 has the following postulational identification: 1. a7 is a supertype of a; that is to say, all a-orders are a7-orders. 2. a1 is iterative.
    [Show full text]
  • Handout from Today's Lecture
    MA532 Lecture Timothy Kohl Boston University April 23, 2020 Timothy Kohl (Boston University) MA532 Lecture April 23, 2020 1 / 26 Cardinal Arithmetic Recall that one may define addition and multiplication of ordinals α = ot(A, A) β = ot(B, B ) α + β and α · β by constructing order relations on A ∪ B and B × A. For cardinal numbers the foundations are somewhat similar, but also somewhat simpler since one need not refer to orderings. Definition For sets A, B where |A| = α and |B| = β then α + β = |(A × {0}) ∪ (B × {1})|. Timothy Kohl (Boston University) MA532 Lecture April 23, 2020 2 / 26 The curious part of the definition is the two sets A × {0} and B × {1} which can be viewed as subsets of the direct product (A ∪ B) × {0, 1} which basically allows us to add |A| and |B|, in particular since, in the usual formula for the size of the union of two sets |A ∪ B| = |A| + |B| − |A ∩ B| which in this case is bypassed since, by construction, (A × {0}) ∩ (B × {1})= ∅ regardless of the nature of A ∩ B. Timothy Kohl (Boston University) MA532 Lecture April 23, 2020 3 / 26 Definition For sets A, B where |A| = α and |B| = β then α · β = |A × B|. One immediate consequence of these definitions is the following. Proposition If m, n are finite ordinals, then as cardinals one has |m| + |n| = |m + n|, (where the addition on the right is ordinal addition in ω) meaning that ordinal addition and cardinal addition agree. Proof. The simplest proof of this is to define a bijection f : (m × {0}) ∪ (n × {1}) → m + n by f (hr, 0i)= r for r ∈ m and f (hs, 1i)= m + s for s ∈ n.
    [Show full text]
  • Semimodular Lattices Theory and Applications
    P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 ENCYCLOPEDIA OF MATHEMATICS AND ITS APPLICATIONS Semimodular Lattices Theory and Applications MANFRED STERN P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 PUBLISHED BY THE PRESS SYNDICATE OF THE UNIVERSITY OF CAMBRIDGE The Pitt Building, Trumpington Street, Cambridge, United Kingdom CAMBRIDGE UNIVERSITY PRESS The Edinburgh Building, Cambridge CB2 2RU, UK http://www.cup.cam.ac.uk 40 West 20th Street, New York, NY 10011-4211, USA http://www.cup.org 10 Stamford Road, Oakleigh, Melbourne 3166, Australia c Cambridge University Press 1999 This book is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published 1999 Printed in the United States of America Typeset in 10/13 Times Roman in LATEX2ε[TB] A catalog record for this book is available from the British Library. Library of Congress Cataloging-in-Publication Data Stern, Manfred. Semimodular lattices: theory and applications. / Manfred Stern. p. cm. – (Encyclopedia of mathematics and its applications ; v. 73) Includes bibliographical references and index. I. Title. II. Series. QA171.5.S743 1999 511.303 – dc21 98-44873 CIP ISBN 0 521 46105 7 hardback P1: SDY/SIL P2: SDY/SJS QC: SSH/SDY CB178/Stern CB178-FM March 3, 1999 9:46 Contents Preface page ix 1 From Boolean Algebras to Semimodular Lattices 1 1.1 Sources of Semimodularity
    [Show full text]
  • Groups with Almost Modular Subgroup Lattice Provided by Elsevier - Publisher Connector
    Journal of Algebra 243, 738᎐764Ž. 2001 doi:10.1006rjabr.2001.8886, available online at http:rrwww.idealibrary.com on View metadata, citation and similar papers at core.ac.uk brought to you by CORE Groups with Almost Modular Subgroup Lattice provided by Elsevier - Publisher Connector Francesco de Giovanni and Carmela Musella Dipartimento di Matematica e Applicazioni, Uni¨ersita` di Napoli ‘‘Federico II’’, Complesso Uni¨ersitario Monte S. Angelo, Via Cintia, I 80126, Naples, Italy and Yaroslav P. Sysak1 Institute of Mathematics, Ukrainian National Academy of Sciences, ¨ul. Tereshchenki¨ska 3, 01601 Kie¨, Ukraine Communicated by Gernot Stroth Received November 14, 2000 DEDICATED TO BERNHARD AMBERG ON THE OCCASION OF HIS 60TH BIRTHDAY 1. INTRODUCTION A subgroup of a group G is called modular if it is a modular element of the lattice ᑦŽ.G of all subgroups of G. It is clear that everynormal subgroup of a group is modular, but arbitrarymodular subgroups need not be normal; thus modularitymaybe considered as a lattice generalization of normality. Lattices with modular elements are also called modular. Abelian groups and the so-called Tarski groupsŽ i.e., infinite groups all of whose proper nontrivial subgroups have prime order. are obvious examples of groups whose subgroup lattices are modular. The structure of groups with modular subgroup lattice has been described completelybyIwasawa wx4, 5 and Schmidt wx 13 . For a detailed account of results concerning modular subgroups of groups, we refer the reader towx 14 . 1 This work was done while the third author was visiting the Department of Mathematics of the Universityof Napoli ‘‘Federico II.’’ He thanks the G.N.S.A.G.A.
    [Show full text]
  • Meet Representations in Upper Continuous Modular Lattices James Elton Delany Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1966 Meet representations in upper continuous modular lattices James Elton Delany Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Mathematics Commons Recommended Citation Delany, James Elton, "Meet representations in upper continuous modular lattices " (1966). Retrospective Theses and Dissertations. 2894. https://lib.dr.iastate.edu/rtd/2894 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. This dissertation has been microiihned exactly as received 66-10,417 DE LA NY, James Elton, 1941— MEET REPRESENTATIONS IN UPPER CONTINU­ OUS MODULAR LATTICES. Iowa State University of Science and Technology Ph.D., 1966 Mathematics University Microfilms, Inc.. Ann Arbor, Michigan MEET REPRESENTATIONS IN UPPER CONTINUOUS MODULAR LATTICES by James Elton Delany A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Mathematics Approved: Signature was redacted for privacy. I _ , r Work Signature was redacted for privacy. Signature was redacted for privacy. Iowa State University of Science and Technology Ames, Iowa 1966 il TABLE OP CONTENTS Page 1. INTRODUCTION 1 2. TORSION ELEMENTS, TORSION FREE ELEMENTS, AND COVERING CONDITIONS 4 3. ATOMIC LATTICES AND UPPER CONTINUITY 8 4. COMPLETE JOIN HOMOMORPHISMS 16 5. TWO HOMOMORPHISMS 27 6.
    [Show full text]
  • This Is the Final Preprint Version of a Paper Which Appeared at Algebraic & Geometric Topology 17 (2017) 439-486
    This is the final preprint version of a paper which appeared at Algebraic & Geometric Topology 17 (2017) 439-486. The published version is accessible to subscribers at http://dx.doi.org/10.2140/agt.2017.17.439 SIMPLICIAL COMPLEXES WITH LATTICE STRUCTURES GEORGE M. BERGMAN Abstract. If L is a finite lattice, we show that there is a natural topological lattice structure on the geo- metric realization of its order complex ∆(L) (definition recalled below). Lattice-theoretically, the resulting object is a subdirect product of copies of L: We note properties of this construction and of some variants, and pose several questions. For M3 the 5-element nondistributive modular lattice, ∆(M3) is modular, but its underlying topological space does not admit a structure of distributive lattice, answering a question of Walter Taylor. We also describe a construction of \stitching together" a family of lattices along a common chain, and note how ∆(M3) can be regarded as an example of this construction. 1. A lattice structure on ∆(L) I came upon the construction studied here from a direction unrelated to the concept of order complex; so I will first motivate it in roughly the way I discovered it, then recall the order complex construction, which turns out to describe the topological structures of these lattices. 1.1. The construction. The motivation for this work comes from Walter Taylor's paper [20], which ex- amines questions of which topological spaces { in particular, which finite-dimensional simplicial complexes { admit various sorts of algebraic structure, including structures of lattice. An earlier version of that paper asked whether there exist spaces which admit structures of lattice, but not of distributive lattice.
    [Show full text]
  • Types for Describing Coordinated Data Structures
    Types for Describing Coordinated Data Structures Michael F. Ringenburg∗ Dan Grossman [email protected] [email protected] Dept. of Computer Science & Engineering University of Washington, Seattle, WA 98195 ABSTRACT the n-th function). This section motivates why such invari- Coordinated data structures are sets of (perhaps unbounded) ants are important, explores why the scope of type variables data structures where the nodes of each structure may share makes the problem appear daunting, and previews the rest abstract types with the corresponding nodes of the other of the paper. structures. For example, consider a list of arguments, and 1.1 Low-Level Type Systems a separate list of functions, where the n-th function of the Recent years have witnessed substantial work on powerful second list should be applied only to the n-th argument of type systems for safe, low-level languages. Standard moti- the first list. We can guarantee that this invariant is obeyed vation for such systems includes compiler debugging (gener- by coordinating the two lists, such that the type of the n-th ated code that does not type check implies a compiler error), argument is existentially quantified and identical to the ar- proof-carrying code (the type system encodes a safety prop- gument type of the n-th function. In this paper, we describe erty that the type-checker verifies), automated optimization a minimal set of features sufficient for a type system to sup- (an optimizer can exploit the type information), and manual port coordinated data structures. We also demonstrate that optimization (humans can use idioms unavailable in higher- two known type systems (Crary and Weirich’s LX [6] and level languages without sacrificing safety).
    [Show full text]
  • The Variety of Modular Lattices Is Not Generated
    TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 255, November 1979 THE VARIETYOF MODULAR LATTICES IS NOT GENERATED BY ITS FINITE MEMBERS BY RALPH FREESE1 Abstract. This paper proves the result of the title. It shows that there is a five-variable lattice identity which holds in all finite modular lattices but not in all modular lattices. It is also shown that every free distributive lattice can be embedded into a free modular lattice. An example showing that modular lattice epimorphisms need not be onto is given. We prove the result of the title by constructing a simple modular lattice of length six not in the variety generated by all finite modular lattices. This lattice can be generated by five elements and thus the free modular lattice on five generators, FM (5), is not residually finite. Our lattice is constructed using the technique of Hall and Dilworth [9] and is closely related to their third example. Let F and K be countably infinite fields of characteristics p and q, where p and q are distinct primes. Let Lp be the lattice of subspaces of a four-dimensional vector space over F, Lq the lattice of subspaces of a four-dimensional vector space over K. Two-dimen- sional quotients (i.e. intervals) in both lattices are always isomorphic to Mu (the two-dimensional lattice with « atoms). Thus Lp and Lq may be glued together over a two-dimensional quotient via [9], and this is our lattice. Notice that if F and K were finite fields we could not carry out the above construction since two-dimensional quotients of Lp would have/)" + 1 atoms and those of Lq would have qm + 1, for some n, m > 1.
    [Show full text]
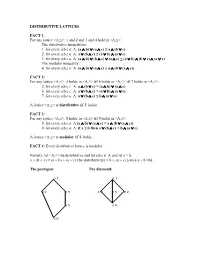
  • DISTRIBUTIVE LATTICES FACT 1: for Any Lattice <A,≤>: 1 and 2 and 3 and 4 Hold in <A,≤>: the Distributive Inequal
    DISTRIBUTIVE LATTICES FACT 1: For any lattice <A,≤>: 1 and 2 and 3 and 4 hold in <A,≤>: The distributive inequalities: 1. for every a,b,c ∈ A: (a ∧ b) ∨ (a ∧ c) ≤ a ∧ (b ∨ c) 2. for every a,b,c ∈ A: a ∨ (b ∧ c) ≤ (a ∨ b) ∧ (a ∨ c) 3. for every a,b,c ∈ A: (a ∧ b) ∨ (b ∧ c) ∨ (a ∧ c) ≤ (a ∨ b) ∧ (b ∨ c) ∧ (a ∨ c) The modular inequality: 4. for every a,b,c ∈ A: (a ∧ b) ∨ (a ∧ c) ≤ a ∧ (b ∨ (a ∧ c)) FACT 2: For any lattice <A,≤>: 5 holds in <A,≤> iff 6 holds in <A,≤> iff 7 holds in <A,≤>: 5. for every a,b,c ∈ A: a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) 6. for every a,b,c ∈ A: a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) 7. for every a,b,c ∈ A: a ∨ (b ∧ c) ≤ b ∧ (a ∨ c). A lattice <A,≤> is distributive iff 5. holds. FACT 3: For any lattice <A,≤>: 8 holds in <A,≤> iff 9 holds in <A,≤>: 8. for every a,b,c ∈ A:(a ∧ b) ∨ (a ∧ c) = a ∧ (b ∨ (a ∧ c)) 9. for every a,b,c ∈ A: if a ≤ b then a ∨ (b ∧ c) = b ∧ (a ∨ c) A lattice <A,≤> is modular iff 8. holds. FACT 4: Every distributive lattice is modular. Namely, let <A,≤> be distributive and let a,b,c ∈ A and let a ≤ b. a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) [by distributivity] = b ∧ (a ∨ c) [since a ∨ b =b]. The pentagon: The diamond: o 1 o 1 o z o y x o o y o z o x o 0 o 0 THEOREM 5: A lattice is modular iff the pentagon cannot be embedded in it.
    [Show full text]
  • Modular Lattices
    Wednesday 1/30/08 Modular Lattices Definition: A lattice L is modular if for every x; y; z 2 L with x ≤ z, (1) x _ (y ^ z) = (x _ y) ^ z: (Note: For all lattices, if x ≤ z, then x _ (y ^ z) ≤ (x _ y) ^ z.) Some basic facts and examples: 1. Every sublattice of a modular lattice is modular. Also, if L is distributive and x ≤ z 2 L, then x _ (y ^ z) = (x ^ z) _ (y ^ z) = (x _ y) ^ z; so L is modular. 2. L is modular if and only if L∗ is modular. Unlike the corresponding statement for distributivity, this is completely trivial, because the definition of modularity is invariant under dualization. 3. N5 is not modular. With the labeling below, we have a ≤ b, but a _ (c ^ b) = a _ 0^ = a; (a _ c) ^ b = 1^ ^ b = b: b c a ∼ 4. M5 = Π3 is modular. However, Π4 is not modular (exercise). Modular lattices tend to come up in algebraic settings: • Subspaces of a vector space • Subgroups of a group • R-submodules of an R-module E.g., if X; Y; Z are subspaces of a vector space V with X ⊆ Z, then the modularity condition says that X + (Y \ Z) = (X + Y ) \ Z: Proposition 1. Let L be a lattice. TFAE: 1. L is modular. 2. For all x; y; z 2 L, if x 2 [y ^ z; z], then x = (x _ y) ^ z. 2∗. For all x; y; z 2 L, if x 2 [y; y _ z], then x = (x ^ z) _ y.
    [Show full text]
  • Generic Haskell: Applications
    Generic Haskell: applications Ralf Hinze1 and Johan Jeuring2,3 1 Institut f¨urInformatik III, Universit¨atBonn R¨omerstraße 164, 53117 Bonn, Germany [email protected] http://www.informatik.uni-bonn.de/~ralf/ 2 Institute of Information and Computing Sciences, Utrecht University P.O.Box 80.089, 3508 TB Utrecht, The Netherlands [email protected] http://www.cs.uu.nl/~johanj/ 3 Open University, Heerlen, The Netherlands Abstract. 1 Generic Haskell is an extension of Haskell that supports the construc- tion of generic programs. This article describes generic programming in practice. It discusses three advanced generic programming applications: generic dictionaries, compressing XML documents, and the zipper. When describing and implementing these examples, we will encounter some advanced features of Generic Haskell, such as type-indexed data types, dependencies between and generic abstractions of generic functions, ad- justing a generic function using a default case, and generic functions with a special case for a particular constructor. 1 Introduction A polytypic (or generic, type-indexed) function is a function that can be instan- tiated on many data types to obtain data type specific functionality. Examples of polytypic functions are the functions that can be derived in Haskell [50], such as show, read, and ‘ ’. In [23] we have introduced type-indexed functions, and we have shown how to implement them in Generic Haskell [7]. For an older introduction to generic programming, see Backhouse et al [4]. Why is generic programming important? Generic programming makes pro- grams easier to write: – Programs that could only be written in an untyped style can now be written in a language with types.
    [Show full text]
  • On the Equational Theory of Projection Lattices of Finite Von Neumann
    The Journal of Symbolic Logic Volume 00, Number 0, XXX 0000 ON THE EQUATIONAL THEORY OF PROJECTION LATTICES OF FINITE VON-NEUMANN FACTORS CHRISTIAN HERRMANN Abstract. For a finite von-Neumann algebra factor M, the projections form a modular ortholattice L(M) . We show that the equational theory of L(M) coincides with that of some resp. all L(Cn×n) and is decidable. In contrast, the uniform word problem for the variety generated by all L(Cn×n) is shown to be undecidable. §1. Introduction. Projection lattices L(M) of finite von-Neumann algebra factors M are continuous orthocomplemented modular lattices and have been considered as logics resp. geometries of quantum meachnics cf. [25]. In the finite dimensional case, the correspondence between irreducible lattices and algebras, to wit the matrix rings Cn×n, has been completely clarified by Birkhoff and von Neumann [5]. Combining this with Tarski’s [27] decidability result for the reals and elementary geometry, decidability of the first order theory of L(M) for a finite dimensional factor M has been observed by Dunn, Hagge, Moss, and Wang [7]. The infinite dimensional case has been studied by von Neumann and Murray in the landmark series of papers on ‘Rings of Operators’ [23], von Neumann’s lectures on ‘Continuous Geometry’ [28], and in the treatment of traces resp. transition probabilities in a ring resp. lattice-theoretic framework [20, 29]. The key to an algebraic treatment is the coordinatization of L(M) by a ∗- regular ring U(M) derived from M and having the same projections: L(M) is isomorphic to the lattice of principal right ideals of U(M) (cf.
    [Show full text]