DOCSLIB.ORG

Measurement of the Cosmic Microwave Background Polarization with the Bicep Telescope at the South Pole by Yuki David Takahashi

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measurement of the Cosmic Microwave Background Polarization with the Bicep Telescope at the South Pole by Yuki David Takahashi Measurement of the Cosmic Microwave Background Polarization with the Bicep Telescope at the South Pole by Yuki David Takahashi A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Physics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor William L. Holzapfel, Chair Professor Adrian T. Lee Professor Chung-Pei Ma Fall 2010 Measurement of the Cosmic Microwave Background Polarization with the Bicep Telescope at the South Pole Copyright 2010 by Yuki David Takahashi 1 Abstract Measurement of the Cosmic Microwave Background Polarization with the Bicep Telescope at the South Pole by Yuki David Takahashi Doctor of Philosophy in Physics University of California, Berkeley Professor William L. Holzapfel, Chair The question of how exactly the universe began is the motivation for this work. Based on the discoveries of the cosmic expansion and of the cosmic microwave background (CMB) ra- diation, humans have learned of the Big Bang origin of the universe. However, what exactly happened in the first moments of the Big Bang? A scenario of initial exponential expansion called “inflation” was proposed in the 1980s, explaining several important mysteries about the universe. Inflation would have generated gravitational waves that would have left a unique imprint in the polarization of the CMB. To search for this evidence for inflation, a team gathered in 2002 to design a telescope experiment called Bicep. Sited at the South Pole, Bicep was a novel 25-cm aperture refractor with 49 pairs of polarization-sensitive bolometers. We completed 3 years of successful observations from February 2006 to De- cember 2008. To constrain the amplitude of polarization resulting from inflation, expected to be at least 7 orders of magnitude fainter than the 3 K CMB intensity, precise control of systematic effects is essential. A crucial challenge is preventing systematic errors from introducing false polarization anisotropy signal at the level corresponding to ∼0.1 µK in amplitude. One main focus of this thesis is the characterization of systematic effects for Bi- cep. We developed a simulation framework for propagating instrumental systematic effects to the final polarization results. Based on these simulations, we established benchmarks for the characterization of critical instrumental properties including bolometer relative gains, beam mismatch, polarization orientation, telescope pointing, sidelobes, thermal stability, and timestream noise model. Guided by these benchmarks, we carefully measured these properties and have shown that we have characterized the instrument adequately to ensure that systematic errors do not limit Bicep's current cosmology results. We have analyzed the first 2 years of data, lowering the upper limits on the gravitational-wave induced polarization by an order of magnitude over all previous experiments. The systematic error analysis has identified what future refinements are likely necessary to probe CMB polarization down to levels corresponding to inflationary energy scales below 2 × 1016 GeV. i Contents List of Figures iii List of Tables v Acknowledgements vi 1 How did the universe begin? 1 1.1 Expanding universe . 2 1.2 Remnant radiation from the Big Bang . 5 1.3 Inflationary beginning of the Big Bang . 7 1.4 Evidence for inflation . 9 1.4.1 Inflationary gravitational waves . 9 1.4.2 Cosmic microwave background polarization . 9 1.4.3 Curl-mode polarization . 11 2 BICEP experiment concept 14 2.1 Design summary . 15 2.2 South Pole site . 16 2.3 Instrument . 18 2.3.1 Polarization sensitive bolometers . 18 2.3.2 Filters and feedhorns . 21 2.3.3 Cold HDPE lenses . 22 2.3.4 Infrared blockers . 24 2.3.5 Readout electronics . 24 2.4 Galactic foregrounds and sky coverage . 25 2.5 Observing strategy . 28 3 Hardware development 31 3.1 Vacuum window . 32 3.2 Ground screen and forebaffle . 34 3.3 Polarization calibrator . 37 3.4 Motion control system . 42 3.5 Optical star-pointing camera . 43 3.6 Refrigerator electronics . 45 3.7 Deployment . 50 ii 4 Instrument characterization 51 4.1 Calibration goals and systematic error simulation . 52 4.2 Relative detector gains . 54 4.2.1 Temporal transfer functions . 56 4.2.2 Relative responsivities . 58 4.2.3 Spectral response . 61 4.3 Beam characterization . 62 4.4 Polarization orientations and efficiencies . 65 4.5 Telescope and detector pointing . 68 4.6 Sidelobe rejection . 69 4.7 Thermal stability . 73 5 Data analysis and results 76 5.1 Collected data, cuts, and observing efficiency . 76 5.2 Data analysis overview . 78 5.3 CMB temperature and polarization maps . 78 5.4 Noise properties and modeling . 80 5.4.1 Properties of noise: spectra and covariance . 81 5.4.2 Simulation of noise-only timestreams . 82 5.4.3 Noise bias in power spectra . 85 5.5 Angular power spectra . 87 5.6 Conclusion . 89 Bibliography 90 iii List of Figures 1.1 Velocity-distance relation among extra-galactic nebulae . 2 1.2 Blackbody spectrum of the CMB measured by COBE .............. 6 1.3 Comoving scales and causal horizon during and after inflation . 8 1.4 Thomson scattering generating polarization . 10 1.5 Three perturbation types resulting in quadrupole anisotropy . 11 1.6 CMB angular power spectra. 12 2.1 Bicep telescope . 15 2.2 South Pole Dark Sector and LC-130 . 17 2.3 Polarization sensitive bolometer . 19 2.4 Layout of the Bicep beams . 20 2.5 Filters and feedhorns . 22 2.6 Optics tube housing two lenses . 23 2.7 Maps of expected levels of polarized foregrounds at 150 GHz . 26 2.8 Bicep's CMB and Galactic fields . 27 2.9 Azimuth scan profile used in mapping the CMB field . 29 2.10 48-hr observing cycle . 30 3.1 Diagram of window, forebaffle, calibrator, and optical camera . 31 3.2 Vacuum window and window cover . 32 3.3 Snow on the window cover sublimating . 33 3.4 Predicted beam patterns out of the aperture . 34 3.5 Grounds shields . 35 3.6 Photograph of absorptive forebaffle and reflective ground screen. 36 3.7 Dielectric sheet calibrator diagram . 38 3.8 Mylar sheet reflectivity for various thicknesses . 38 3.9 Dielectric sheet calibrator expected signal . 40 3.10 Dielectric sheet calibrator for measuring PSB orientations . 41 3.11 3-axis telescope mount, interlock system, and manual controller . 43 3.12 Motion control interlock scheme . 44 3.13 Optical star-pointing camera . 45 3.14 Adsorption refrigerator . 46 3.15 Electronics schematic for resistance thermometer readout . 47 3.16 Electronics schematic for heater drivers . 48 3.17 Electronics schematic for LHe level sensor readout . 49 3.18 Refrigerator electronics . 49 iv 4.1 Spurious BB power from simulations of measured potential systematic errors . 55 4.2 Temporal response function measurement setup . 57 4.3 Measured transfer functions . 58 4.4 Bolometer timestream during relative responsivity calibration . 59 4.5 Relative responsivity measurement consistency . 60 4.6 PSB pair-differencing . 61 4.7 Average measured spectral response . 62 4.8 Beam mapping setup on site . 63 4.9 Differential beam map . 64 4.10 Dielectric sheet calibrator response . 66 4.11 Setup above the cryostat window for measuring cross-polarization responses . 67 4.12 Calibration source on a mast for measuring cross-polarization responses . 67 4.13 Sidelobe measurement using broadband noise source on a mast . 69 4.14 Map of fractional polarization . 70 4.15 Azimuthally-averaged sidelobe response . 71 4.16 Integrated beam . 72 4.17 Convolution of sidelobes with Galactic emissions . 73 4.18 Power spectra of sidelobe response to Galactic emissions . 73 4.19 Focal plane thermistor map . 75 4.20 Power spectra of focal plane temperature fluctuations . 75 5.1 Bicep map of the entire mapped field . 77 5.2 Data analysis flow chart . 78 5.3 Maps from the first 2 years of data, including frequency jackknife differences . 79 5.4 Average noise frequency spectra of all PSB pairs . 82 5.5 Example correlation matrices from the Bicep noise model . 83 5.6 Noise model spectrum and the simulated timestream spectra . 84 5.7 Real and simulated-noise timestreams for a PSB pair . 85 5.8 Power spectra of simulated signal+noise, noise only, and data jackknife . 86 5.9 Bicep 2-year CMB polarization.
Load more

Recommended publications
  • 1 Lecture 26
    PHYS 445 Lecture 26 - Black-body radiation I 26 - 1 Lecture 26 - Black-body radiation I What's Important: · number density · energy density Text: Reif In our previous discussion of photons, we established that the mean number of photons with energy i is 1 n = (26.1) i eß i - 1 Here, the questions that we want to address about photons are: · what is their number density · what is their energy density · what is their pressure? Number density n Eq. (26.1) is written in the language of discrete states. The first thing we need to do is replace the sum by an integral over photon momentum states: 3 S i ® ò d p Of course, it isn't quite this simple because the density-of-states issue that we introduced before: for every spin state there is one phase space state for every h 3, so the proper replacement more like 3 3 3 S i ® (1/h ) ò d p ò d r The units now work: the left hand side is a number, and so is the right hand side. But this expression ignores spin - it just deals with the states in phase space. For every photon momentum, there are two ways of arranging its polarization (i.e., the orientation of its electric or magnetic field vectors): where the photon momentum vector is perpendicular to the plane. Thus, we have 3 3 3 S i ® (2/h ) ò d p ò d r. (26.2) Assuming that our system is spatially uniform, the position integral can be replaced by the volume ò d 3r = V.
    [Show full text]
  • Measurement of the Speed of Gravity
    Measurement of the Speed of Gravity Yin Zhu Agriculture Department of Hubei Province, Wuhan, China Abstract From the Liénard-Wiechert potential in both the gravitational field and the electromagnetic field, it is shown that the speed of propagation of the gravitational field (waves) can be tested by comparing the measured speed of gravitational force with the measured speed of Coulomb force. PACS: 04.20.Cv; 04.30.Nk; 04.80.Cc Fomalont and Kopeikin [1] in 2002 claimed that to 20% accuracy they confirmed that the speed of gravity is equal to the speed of light in vacuum. Their work was immediately contradicted by Will [2] and other several physicists. [3-7] Fomalont and Kopeikin [1] accepted that their measurement is not sufficiently accurate to detect terms of order , which can experimentally distinguish Kopeikin interpretation from Will interpretation. Fomalont et al [8] reported their measurements in 2009 and claimed that these measurements are more accurate than the 2002 VLBA experiment [1], but did not point out whether the terms of order have been detected. Within the post-Newtonian framework, several metric theories have studied the radiation and propagation of gravitational waves. [9] For example, in the Rosen bi-metric theory, [10] the difference between the speed of gravity and the speed of light could be tested by comparing the arrival times of a gravitational wave and an electromagnetic wave from the same event: a supernova. Hulse and Taylor [11] showed the indirect evidence for gravitational radiation. However, the gravitational waves themselves have not yet been detected directly. [12] In electrodynamics the speed of electromagnetic waves appears in Maxwell equations as c = √휇0휀0, no such constant appears in any theory of gravity.
    [Show full text]
  • Baryogenesis in a CP Invariant Theory That Utilizes the Stochastic Movement of Light fields During Inflation
    Baryogenesis in a CP invariant theory Anson Hook School of Natural Sciences Institute for Advanced Study Princeton, NJ 08540 June 12, 2018 Abstract We consider baryogenesis in a model which has a CP invariant Lagrangian, CP invariant initial conditions and does not spontaneously break CP at any of the minima. We utilize the fact that tunneling processes between CP invariant minima can break CP to implement baryogenesis. CP invariance requires the presence of two tunneling processes with opposite CP breaking phases and equal probability of occurring. In order for the entire visible universe to see the same CP violating phase, we consider a model where the field doing the tunneling is the inflaton. arXiv:1508.05094v1 [hep-ph] 20 Aug 2015 1 1 Introduction The visible universe contains more matter than anti-matter [1]. The guiding principles for gener- ating this asymmetry have been Sakharov’s three conditions [2]. These three conditions are C/CP violation • Baryon number violation • Out of thermal equilibrium • Over the years, counter examples have been found for Sakharov’s conditions. One can avoid the need for number violating interactions in theories where the negative B L number is stored − in a sector decoupled from the standard model, e.g. in right handed neutrinos as in Dirac lep- togenesis [3, 4] or in dark matter [5]. The out of equilibrium condition can be avoided if one uses spontaneous baryogenesis [6], where a chemical potential is used to create a non-zero baryon number in thermal equilibrium. However, these models still require a C/CP violating phase or coupling in the Lagrangian.
    [Show full text]
  • The Q/U Imaging Experiment (QUIET): the Q-Band Receiver Array Instrument and Observations by Laura Newburgh Advisor: Professor Amber Miller
    The Q/U Imaging ExperimenT (QUIET): The Q-band Receiver Array Instrument and Observations by Laura Newburgh Advisor: Professor Amber Miller Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2010 c 2010 Laura Newburgh All Rights Reserved Abstract The Q/U Imaging ExperimenT (QUIET): The Q-band Receiver Array Instrument and Observations by Laura Newburgh Phase I of the Q/U Imaging ExperimenT (QUIET) measures the Cosmic Microwave Background polarization anisotropy spectrum at angular scales 25 1000. QUIET has deployed two independent receiver arrays. The 40-GHz array took data between October 2008 and June 2009 in the Atacama Desert in northern Chile. The 90-GHz array was deployed in June 2009 and observations are ongoing. Both receivers observe four 15◦ 15◦ regions of the sky in the southern hemisphere that are expected × to have low or negligible levels of polarized foreground contamination. This thesis will describe the 40 GHz (Q-band) QUIET Phase I instrument, instrument testing, observations, analysis procedures, and preliminary power spectra. Contents 1 Cosmology with the Cosmic Microwave Background 1 1.1 The Cosmic Microwave Background . 1 1.2 Inflation . 2 1.2.1 Single Field Slow Roll Inflation . 3 1.2.2 Observables . 4 1.3 CMB Anisotropies . 6 1.3.1 Temperature . 6 1.3.2 Polarization . 7 1.3.3 Angular Power Spectrum Decomposition . 8 1.4 Foregrounds . 14 1.5 CMB Science with QUIET . 15 2 The Q/U Imaging ExperimenT Q-band Instrument 19 2.1 QUIET Q-band Instrument Overview .
    [Show full text]
  • String Theory and Pre-Big Bang Cosmology
    IL NUOVO CIMENTO 38 C (2015) 160 DOI 10.1393/ncc/i2015-15160-8 Colloquia: VILASIFEST String theory and pre-big bang cosmology M. Gasperini(1)andG. Veneziano(2) (1) Dipartimento di Fisica, Universit`a di Bari - Via G. Amendola 173, 70126 Bari, Italy and INFN, Sezione di Bari - Bari, Italy (2) CERN, Theory Unit, Physics Department - CH-1211 Geneva 23, Switzerland and Coll`ege de France - 11 Place M. Berthelot, 75005 Paris, France received 11 January 2016 Summary. — In string theory, the traditional picture of a Universe that emerges from the inflation of a very small and highly curved space-time patch is a possibility, not a necessity: quite different initial conditions are possible, and not necessarily unlikely. In particular, the duality symmetries of string theory suggest scenarios in which the Universe starts inflating from an initial state characterized by very small curvature and interactions. Such a state, being gravitationally unstable, will evolve towards higher curvature and coupling, until string-size effects and loop corrections make the Universe “bounce” into a standard, decreasing-curvature regime. In such a context, the hot big bang of conventional cosmology is replaced by a “hot big bounce” in which the bouncing and heating mechanisms originate from the quan- tum production of particles in the high-curvature, large-coupling pre-bounce phase. Here we briefly summarize the main features of this inflationary scenario, proposed a quarter century ago. In its simplest version (where it represents an alternative and not a complement to standard slow-roll inflation) it can produce a viable spectrum of density perturbations, together with a tensor component characterized by a “blue” spectral index with a peak in the GHz frequency range.
    [Show full text]
  • Big Bang Blunder Bursts the Multiverse Bubble
    WORLD VIEW A personal take on events IER P P. PA P. Big Bang blunder bursts the multiverse bubble Premature hype over gravitational waves highlights gaping holes in models for the origins and evolution of the Universe, argues Paul Steinhardt. hen a team of cosmologists announced at a press world will be paying close attention. This time, acceptance will require conference in March that they had detected gravitational measurements over a range of frequencies to discriminate from fore- waves generated in the first instants after the Big Bang, the ground effects, as well as tests to rule out other sources of confusion. And Worigins of the Universe were once again major news. The reported this time, the announcements should be made after submission to jour- discovery created a worldwide sensation in the scientific community, nals and vetting by expert referees. If there must be a press conference, the media and the public at large (see Nature 507, 281–283; 2014). hopefully the scientific community and the media will demand that it According to the team at the BICEP2 South Pole telescope, the is accompanied by a complete set of documents, including details of the detection is at the 5–7 sigma level, so there is less than one chance systematic analysis and sufficient data to enable objective verification. in two million of it being a random occurrence. The results were The BICEP2 incident has also revealed a truth about inflationary the- hailed as proof of the Big Bang inflationary theory and its progeny, ory. The common view is that it is a highly predictive theory.
    [Show full text]
  • Aspects of Spatially Homogeneous and Isotropic Cosmology
    Faculty of Technology and Science Department of Physics and Electrical Engineering Mikael Isaksson Aspects of Spatially Homogeneous and Isotropic Cosmology Degree Project of 15 credit points Physics Program Date/Term: 02-04-11 Supervisor: Prof. Claes Uggla Examiner: Prof. Jürgen Fuchs Karlstads universitet 651 88 Karlstad Tfn 054-700 10 00 Fax 054-700 14 60 [email protected] www.kau.se Abstract In this thesis, after a general introduction, we first review some differential geom- etry to provide the mathematical background needed to derive the key equations in cosmology. Then we consider the Robertson-Walker geometry and its relation- ship to cosmography, i.e., how one makes measurements in cosmology. We finally connect the Robertson-Walker geometry to Einstein's field equation to obtain so- called cosmological Friedmann-Lema^ıtre models. These models are subsequently studied by means of potential diagrams. 1 CONTENTS CONTENTS Contents 1 Introduction 3 2 Differential geometry prerequisites 8 3 Cosmography 13 3.1 Robertson-Walker geometry . 13 3.2 Concepts and measurements in cosmography . 18 4 Friedmann-Lema^ıtre dynamics 30 5 Bibliography 42 2 1 INTRODUCTION 1 Introduction Cosmology comes from the Greek word kosmos, `universe' and logia, `study', and is the study of the large-scale structure, origin, and evolution of the universe, that is, of the universe taken as a whole [1]. Even though the word cosmology is relatively recent (first used in 1730 in Christian Wolff's Cosmologia Generalis), the study of the universe has a long history involving science, philosophy, eso- tericism, and religion. Cosmologies in their earliest form were concerned with, what is now known as celestial mechanics (the study of the heavens).
    [Show full text]
  • Lecture 17 : the Cosmic Microwave Background
    Let’s think about the early Universe… Lecture 17 : The Cosmic ! From Hubble’s observations, we know the Universe is Microwave Background expanding ! This can be understood theoretically in terms of solutions of GR equations !Discovery of the Cosmic Microwave ! Earlier in time, all the matter must have been Background (ch 14) squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! !The Hot Big Bang This week: read Chapter 12/14 in textbook 4/15/14 1 4/15/14 3 Let’s think about the early Universe… Let’s think about the early Universe… ! From Hubble’s observations, we know the Universe is ! From Hubble’s observations, we know the Universe is expanding expanding ! This can be understood theoretically in terms of solutions of ! This can be understood theoretically in terms of solutions of GR equations GR equations ! Earlier in time, all the matter must have been squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! ! What was the Universe like long, long ago? ! What were the original contents? ! What were the early conditions like? ! What physical processes occurred under those conditions? ! How did changes over time result in the contents and structure we see today? 4/15/14 2 4/15/14 4 The Poetic Version ! In a brilliant flash about fourteen billion years ago, time and matter were born in a single instant of creation.
    [Show full text]
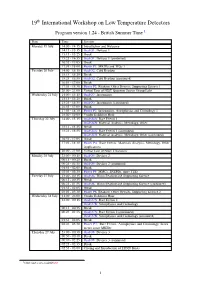
  • 19 International Workshop on Low Temperature Detectors
    19th International Workshop on Low Temperature Detectors Program version 1.24 - British Summer Time 1 Date Time Session Monday 19 July 14:00 - 14:15 Introduction and Welcome 14:15 - 15:15 Oral O1: Devices 1 15:15 - 15:25 Break 15:25 - 16:55 Oral O1: Devices 1 (continued) 16:55 - 17:05 Break 17:05 - 18:00 Poster P1: MKIDs and TESs 1 Tuesday 20 July 14:00 - 15:15 Oral O2: Cold Readout 15:15 - 15:25 Break 15:25 - 16:55 Oral O2: Cold Readout (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P2: Readout, Other Devices, Supporting Science 1 20:00 - 21:00 Virtual Tour of NIST Quantum Sensor Group Labs Wednesday 21 July 14:00 - 15:15 Oral O3: Instruments 15:15 - 15:25 Break 15:25 - 16:55 Oral O3: Instruments (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P3: Instruments, Astrophysics and Cosmology 1 18:00 - 19:00 Vendor Exhibitor Hour Thursday 22 July 14:00 - 15:15 Oral O4A: Rare Events 1 Oral O4B: Material Analysis, Metrology, Other 15:15 - 15:25 Break 15:25 - 16:55 Oral O4A: Rare Events 1 (continued) Oral O4B: Material Analysis, Metrology, Other (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P4: Rare Events, Materials Analysis, Metrology, Other Applications 20:00 - 21:00 Virtual Tour of NIST Cleanoom Monday 26 July 23:00 - 00:15 Oral O5: Devices 2 00:15 - 00:25 Break 00:25 - 01:55 Oral O5: Devices 2 (continued) 01:55 - 02:05 Break 02:05 - 03:30 Poster P5: MMCs, SNSPDs, more TESs Tuesday 27 July 23:00 - 00:15 Oral O6: Warm Readout and Supporting Science 00:15 - 00:25 Break 00:25 - 01:55 Oral O6: Warm Readout and Supporting Science
    [Show full text]
  • Maturity of Lumped Element Kinetic Inductance Detectors For
    Astronomy & Astrophysics manuscript no. Catalano˙f c ESO 2018 September 26, 2018 Maturity of lumped element kinetic inductance detectors for space-borne instruments in the range between 80 and 180 GHz A. Catalano1,2, A. Benoit2, O. Bourrion1, M. Calvo2, G. Coiffard3, A. D’Addabbo4,2, J. Goupy2, H. Le Sueur5, J. Mac´ıas-P´erez1, and A. Monfardini2,1 1 LPSC, Universit Grenoble-Alpes, CNRS/IN2P3, 2 Institut N´eel, CNRS, Universit´eJoseph Fourier Grenoble I, 25 rue des Martyrs, Grenoble, 3 Institut de Radio Astronomie Millim´etrique (IRAM), Grenoble, 4 LNGS - Laboratori Nazionali del Gran Sasso - Assergi (AQ), 5 Centre de Sciences Nucl´eaires et de Sciences de la Mati`ere (CSNSM), CNRS/IN2P3, bat 104 - 108, 91405 Orsay Campus Preprint online version: September 26, 2018 ABSTRACT This work intends to give the state-of-the-art of our knowledge of the performance of lumped element kinetic inductance detectors (LEKIDs) at millimetre wavelengths (from 80 to 180 GHz). We evaluate their optical sensitivity under typical background conditions that are representative of a space environment and their interaction with ionising particles. Two LEKID arrays, originally designed for ground-based applications and composed of a few hundred pixels each, operate at a central frequency of 100 and 150 GHz (∆ν/ν about 0.3). Their sensitivities were characterised in the laboratory using a dedicated closed-cycle 100 mK dilution cryostat and a sky simulator, allowing for the reproduction of realistic, space-like observation conditions. The impact of cosmic rays was evaluated by exposing the LEKID arrays to alpha particles (241Am) and X sources (109Cd), with a read-out sampling frequency similar to those used for Planck HFI (about 200 Hz), and also with a high resolution sampling level (up to 2 MHz) to better characterise and interpret the observed glitches.
    [Show full text]
  • CMB Telescopes and Optical Systems to Appear In: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation
    CMB Telescopes and Optical Systems To appear in: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation Shaul Hanany ([email protected]) University of Minnesota, School of Physics and Astronomy, Minneapolis, MN, USA, Michael Niemack ([email protected]) National Institute of Standards and Technology and University of Colorado, Boulder, CO, USA, and Lyman Page ([email protected]) Princeton University, Department of Physics, Princeton NJ, USA. March 26, 2012 Abstract The cosmic microwave background radiation (CMB) is now firmly established as a funda- mental and essential probe of the geometry, constituents, and birth of the Universe. The CMB is a potent observable because it can be measured with precision and accuracy. Just as importantly, theoretical models of the Universe can predict the characteristics of the CMB to high accuracy, and those predictions can be directly compared to observations. There are multiple aspects associated with making a precise measurement. In this review, we focus on optical components for the instrumentation used to measure the CMB polarization and temperature anisotropy. We begin with an overview of general considerations for CMB ob- servations and discuss common concepts used in the community. We next consider a variety of alternatives available for a designer of a CMB telescope. Our discussion is guided by arXiv:1206.2402v1 [astro-ph.IM] 11 Jun 2012 the ground and balloon-based instruments that have been implemented over the years. In the same vein, we compare the arc-minute resolution Atacama Cosmology Telescope (ACT) and the South Pole Telescope (SPT). CMB interferometers are presented briefly. We con- clude with a comparison of the four CMB satellites, Relikt, COBE, WMAP, and Planck, to demonstrate a remarkable evolution in design, sensitivity, resolution, and complexity over the past thirty years.
    [Show full text]
  • A Brief History of Gravitational Waves
    universe Review A Brief History of Gravitational Waves Jorge L. Cervantes-Cota 1, Salvador Galindo-Uribarri 1 and George F. Smoot 2,3,4,* 1 Department of Physics, National Institute for Nuclear Research, Km 36.5 Carretera Mexico-Toluca, Ocoyoacac, C.P. 52750 Mexico, Mexico; [email protected] (J.L.C.-C.); [email protected] (S.G.-U.) 2 Helmut and Ana Pao Sohmen Professor at Large, Institute for Advanced Study, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, 999077 Hong Kong, China 3 Université Sorbonne Paris Cité, Laboratoire APC-PCCP, Université Paris Diderot, 10 rue Alice Domon et Leonie Duquet, 75205 Paris Cedex 13, France 4 Department of Physics and LBNL, University of California; MS Bldg 50-5505 LBNL, 1 Cyclotron Road Berkeley, 94720 CA, USA * Correspondence: [email protected]; Tel.:+1-510-486-5505 Academic Editors: Lorenzo Iorio and Elias C. Vagenas Received: 21 July 2016; Accepted: 2 September 2016; Published: 13 September 2016 Abstract: This review describes the discovery of gravitational waves. We recount the journey of predicting and finding those waves, since its beginning in the early twentieth century, their prediction by Einstein in 1916, theoretical and experimental blunders, efforts towards their detection, and finally the subsequent successful discovery. Keywords: gravitational waves; General Relativity; LIGO; Einstein; strong-field gravity; binary black holes 1. Introduction Einstein’s General Theory of Relativity, published in November 1915, led to the prediction of the existence of gravitational waves that would be so faint and their interaction with matter so weak that Einstein himself wondered if they could ever be discovered.
    [Show full text]