Synaptic Counts Approximate Synaptic Contact Area in Drosophila
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Monitoring Synaptic and Neuronal Activity in 3D with Synthetic And
Journal of Neuroscience Methods 222 (2014) 69–81 Contents lists available at ScienceDirect Journal of Neuroscience Methods jou rnal homepage: www.elsevier.com/locate/jneumeth Basic Neuroscience Monitoring synaptic and neuronal activity in 3D with synthetic and genetic indicators using a compact acousto-optic lens two-photon microscopeଝ Tomás Fernández-Alfonso, K.M. Naga Srinivas Nadella, M. Florencia Iacaruso, ∗ Bruno Pichler, Hana Ros,ˇ Paul A. Kirkby, R. Angus Silver Department of Neuroscience, Physiology and Pharmacology, University College London, London WC1E 6BT, UK h i g h l i g h t s g r a p h i c a l a b s t r a c t • We expand the utility of acousto- optic lens (AOL) 3D 2P microscopy. • We show rapid, simultaneous moni- toring of synaptic inputs distributed in 3D. • First use of genetically encoded indicators with AOL 3D functional imaging. • Measurement of sensory-evoked neuronal population activity in 3D in vivo. • Strategies for improving the mea- surement of the timing of neuronal signals. a r t i c l e i n f o a b s t r a c t Article history: Background: Two-photon microscopy is widely used to study brain function, but conventional micro- Received 26 June 2013 scopes are too slow to capture the timing of neuronal signalling and imaging is restricted to one plane. Received in revised form 22 October 2013 Recent development of acousto-optic-deflector-based random access functional imaging has improved Accepted 26 October 2013 the temporal resolution, but the utility of these technologies for mapping 3D synaptic activity patterns and their performance at the excitation wavelengths required to image genetically encoded indicators Keywords: have not been investigated. -

How-To Gnome-Look Guide
HHOOWW--TTOO Written by David D Lowe GGNNOOMMEE--LLOOOOKK GGUUIIDDEE hen I first joined the harddisk, say, ~/Pictures/Wallpapers. right-clicking on your desktop Ubuntu community, I and selecting the appropriate You may have noticed that gnome- button (you know which one!). Wwas extremely look.org separates wallpapers into impressed with the amount of different categories, according to the customization Ubuntu had to size of the wallpaper in pixels. For Don't let acronyms intimidate offer. People posted impressive the best quality, you want this to you; you don't have to know screenshots, and mentioned the match your screen resolution. If you what the letters stand for to themes they were using. They don't know what your screen know what it is. Basically, GTK is soon led me to gnome-look.org, resolution is, click System > the system GNOME uses to the number one place for GNOME Preferences > Screen Resolution. display things like buttons and visual customization. The However, Ubuntu stretches controls. GNOME is Ubuntu's screenshots there looked just as wallpapers quite nicely if you picked default desktop environment. I impressive, but I was very the wrong size, so you needn't fret will only be dealing with GNOME confused as to what the headings about it. on the sidebar meant, and I had customization here--sorry no idea how to use the files I SVG is a special image format that Kubuntu and Xubuntu folks! downloaded. Hopefully, this guide doesn't use pixels; it uses shapes Gnome-look.org distinguishes will help you learn what I found called vectors, which means you can between two versions of GTK: out the slow way. -
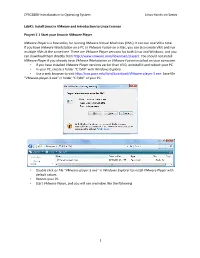
Install Linux in Vmware and Introduction to Linux Essence
CPSC2800‐Introducation to Operating System Linux Hands‐on Series Lab#1: Install Linux in VMware and Introduction to Linux Essence Project 1‐1 Start your Linux in VMware Player VMware Player is a free utility for running VMware Virtual Machines (VMs). It can run one VM a time. If you have VMware Workstation on a PC or VMware Fusion on a Mac, you can also create VMs and run multiple VMs at the same time. There are VMware Player versions for both Linux and Windows, and you can download them directly from http://www.vmware.com/ddownload/player/. You should not install VMware Player if you already have VMware Workstation or VMware Fusion installed on your computer. • If you have installed VMware Player versions earlier than V3.0, uninstall it and reboot your PC. • In your PC, create a folder “C:\VM” with Windows Expxplorer. • Use a web browser to visit http://csis.pace.edu/lixin/download/VVMware‐player‐3.exe. Save file “VMware‐player‐3.exe” in folder “C:\VM” of your PC. • Double click on file “VMware‐player‐3.exe” in Windoows Explorer to install VMware Player with default values. • Reboot your PC. • Start VMware Player, and you will see a window like the following. 1 CPSC2800‐Introducation to Operating System Linux Hands‐on Series • Click on menu item “File|Preferences…” 2 CPSC2800‐Introducation to Operating System Linux Hands‐on Series • In the “Preferences” window, uncheck for software updates, and click on the “Download Alll Components Now” button so you can later install VMware Tools in your new VMs without Internet access. -

Free As in Freedom
Daily Diet Free as in freedom ... • The freedom to run the program, for any purpose (freedom 0). Application Seen elsewhere Free Software Choices • The freedom to study how the program works, and adapt it to Text editor Wordpad Kate / Gedit/Vi/ Emacs your needs (freedom 1). Access to the source code is a precondition for this. Office Suite Microsoft Office KOffice / Open Office • The freedom to redistribute copies so you can help your Word Processor Microsoft Word Kword / Writer Presentation PowerPoint KPresenter / Impress neighbor (freedom 2). Spreadsheet Excel Kexl / Calc • The freedom to improve the program, and release your Mail & Info Manager Outlook Thunderbird / Evolution improvements to the public, so that the whole community benefits (freedom 3). Access to the source code is a Browser Safari, IE Konqueror / Firefox precondition for this. Chat client MSN, Yahoo, Gtalk, Kopete / Gaim IRC mIRC Xchat Non-Kernel parts = GNU (GNU is Not Unix) [gnu.org] Netmeeting Ekiga Kernel = Linux [kernel.org] PDF reader Acrobat Reader Kpdf / Xpdf/ Evince GNU Operating Syetem = GNU/Linux or GNU+Linux CD - burning Nero K3b / Gnome Toaster Distro – A flavor [distribution] of GNU/Linux os Music, video Winamp, Media XMMS, mplayer, xine, player rythmbox, totem Binaries ± Executable Terminal>shell>command line – interface to type in command Partition tool Partition Magic Gparted root – the superuser, administrator Graphics and Design Photoshop, GIMP, Image Magick & Corel Draw Karbon14,Skencil,MultiGIF The File system Animation Flash Splash Flash, f4l, Blender Complete list- linuxrsp.ru/win-lin-soft/table-eng.html, linuxeq.com/ Set up Broadband Ubuntu – set up- in terminal sudo pppoeconf. -

Technology User Guide Volume III: DRC INSIGHT
Technology User Guide Volume III: DRC INSIGHT WISCONSIN Data Recognition Corporation (DRC) 13490 Bass Lake Road Maple Grove, MN 55311 Wisconsin Service Line: 1-800-459-6530 DRC INSIGHT Portal: https://wi.drcedirect.com Email: [email protected] Revision Date: November 12, 2020 COPYRIGHT Copyright © 2020 Data Recognition Corporation The following items in DRC INSIGHT are protected by copyright law: • The User Guide. • All text and titles on the software’s entry and display, including the look and feel of the interaction of the windows, supporting menus, pop-up windows, and layout. DRC INSIGHT Online Learning System and DRC INSIGHT Portal are trademarked by Data Recognition Corporation. Any individuals or corporations who violate these copyrights and trademarks will be prosecuted under both criminal and civil laws, and any resulting products will be required to be withdrawn from the marketplace. The following are trademarks or registered trademarks of Microsoft Corporation in the United States and/or other countries: Internet Explorer Microsoft Windows Windows Vista Windows XP Windows 7 Windows 8 Windows 10 The following are trademarks or registered trademarks of Apple Corporation in the United States and/or other countries: Apple Macintosh Mac OS X and macOS iPad iPadOS iOS* *iOS is a trademark or registered trademark of Cisco in the U.S. and other countries and is used under license. Safari The following are trademarks or registered trademarks of Google Corporation in the United States and/or other countries. Chrome Chromebook Google Play The following is a trademark or registered trademark of Mozilla Corporation in the United States and/or other countries. -

Physical Determinants of Vesicle Mobility and Supply at a Central
RESEARCH ARTICLE Physical determinants of vesicle mobility and supply at a central synapse Jason Seth Rothman1, Laszlo Kocsis2, Etienne Herzog3,4, Zoltan Nusser2*, Robin Angus Silver1* 1Department of Neuroscience, Physiology and Pharmacology, University College London, London, United Kingdom; 2Laboratory of Cellular Neurophysiology, Institute of Experimental Medicine, Hungarian Academy of Sciences, Budapest, Hungary; 3Department of Molecular Neurobiology, Max Planck Institute of Experimental Medicine, Go¨ ttingen, Germany; 4Team Synapse in Cognition, Interdisciplinary Institute for Neuroscience, Universite´ de Bordeaux, UMR 5297, F-33000, Bordeaux, France Abstract Encoding continuous sensory variables requires sustained synaptic signalling. At several sensory synapses, rapid vesicle supply is achieved via highly mobile vesicles and specialized ribbon structures, but how this is achieved at central synapses without ribbons is unclear. Here we examine vesicle mobility at excitatory cerebellar mossy fibre synapses which sustain transmission over a broad frequency bandwidth. Fluorescent recovery after photobleaching in slices from VGLUT1Venus knock-in mice reveal 75% of VGLUT1-containing vesicles have a high mobility, comparable to that at ribbon synapses. Experimentally constrained models establish hydrodynamic interactions and vesicle collisions are major determinants of vesicle mobility in crowded presynaptic terminals. Moreover, models incorporating 3D reconstructions of vesicle clouds near active zones (AZs) predict the measured releasable pool size and replenishment rate from the reserve pool. They also show that while vesicle reloading at AZs is not diffusion-limited at the onset of release, *For correspondence: nusser@ diffusion limits vesicle reloading during sustained high-frequency signalling. koki.hu (ZN); [email protected] DOI: 10.7554/eLife.15133.001 (RAS) Competing interests: The authors declare that no competing interests exist. -

Predominantly Linear Summation of Metabotropic Postsynaptic
RESEARCH ARTICLE Predominantly linear summation of metabotropic postsynaptic potentials follows coactivation of neurogliaform interneurons Attila Ozsva´ r, Gergely Komlo´ si, Ga´ spa´ r Ola´ h, Judith Baka, Ga´ bor Molna´ r, Ga´ bor Tama´ s* MTA-SZTE Research Group for Cortical Microcircuits of the Hungarian Academy of Sciences,, Department of Physiology, Anatomy and Neuroscience, University of Szeged, Szeged, Hungary Abstract Summation of ionotropic receptor-mediated responses is critical in neuronal computation by shaping input-output characteristics of neurons. However, arithmetics of summation for metabotropic signals are not known. We characterized the combined ionotropic and metabotropic output of neocortical neurogliaform cells (NGFCs) using electrophysiological and anatomical methods in the rat cerebral cortex. These experiments revealed that GABA receptors are activated outside release sites and confirmed coactivation of putative NGFCs in superficial cortical layers in vivo. Triple recordings from presynaptic NGFCs converging to a postsynaptic neuron revealed sublinear summation of ionotropic GABAA responses and linear summation of metabotropic GABAB responses. Based on a model combining properties of volume transmission and distributions of all NGFC axon terminals, we predict that in 83% of cases one or two NGFCs can provide input to a point in the neuropil. We suggest that interactions of metabotropic GABAergic responses remain linear even if most superficial layer interneurons specialized to recruit GABAB receptors are simultaneously active. *For correspondence: [email protected] Competing interests: The authors declare that no Introduction competing interests exist. Each neuron in the cerebral cortex receives thousands of excitatory synaptic inputs that drive action Funding: See page 20 potential (AP) output. The efficacy and timing of excitation is effectively governed by GABAergic Received: 10 December 2020 inhibitory inputs that arrive with spatiotemporal precision onto different subcellular domains. -

Neuroinformatics: Sharing, Organizing and Accessing Data and Models
Neuroinformatics: sharing, organizing and accessing data and models Arnd Roth Wolfson Institute for Biomedical Research University College London The optogenetics revolution Fuhrmann et al., 2015 The optogenetics revolution Fuhrmann et al., 2015 The connectomics revolution Helmstaedter et al., 2013 The connectomics revolution Helmstaedter et al., 2013 Connectomics data mining Jonas & Körding, 2015 Connectomics data mining Jonas & Körding, 2015 Deep artificial neural networks Mnih et al., 2015 Neuroinformatics: sharing, organizing and accessing experimental data Allen Institute http://alleninstitute.org Janelia Research Campus https://www.janelia.org/ Open Connectome Project http://www.openconnectomeproject.org/ Cell Image Library http://www.cellimagelibrary.org/ Human Brain Project http://www.humanbrainproject.eu/ INCF http://www.incf.org/ Single neuron and network simulators NEURON http://www.neuron.yale.edu/neuron/ GENESIS https://www.genesis-sim.org/ MOOSE http://moose.ncbs.res.in/ PSICS http://www.psics.org/ NEST http://www.nest-initiative.org/ Meta-simulators: simulator- independent model description PyNN http://neuralensemble.org/PyNN/ neuroConstruct http://www.neuroconstruct.org/ NeuroML http://www.neuroml.org/ NineML http://software.incf.org/software/nineml neuroConstruct http://www.opensourcebrain.org 12 neuroConstruct Software tool (written in Java) developed in Angus Silver’s Laboratory of Synaptic Transmission and Information Processing Facilitates development of 3D network models of biologically realistic cells through graphical -

Ubuntu® 1.4Inux Bible
Ubuntu® 1.4inux Bible William von Hagen 111c10,ITENNIAL. 18072 @WILEY 2007 •ICIOATENNIAl. Wiley Publishing, Inc. Acknowledgments xxi Introduction xxiii Part 1: Getting Started with Ubuntu Linux Chapter 1: The Ubuntu Linux Project 3 Background 4 Why Use Linux 4 What Is a Linux Distribution? 5 Introducing Ubuntu Linux 6 The Ubuntu Manifesto 7 Ubuntu Linux Release Schedule 8 Ubuntu Update and Maintenance Commitments 9 Ubuntu and the Debian Project 9 Why Choose Ubuntu? 10 Installation Requirements 11 Supported System Types 12 Hardware Requirements 12 Time Requirements 12 Ubuntu CDs 13 Support for Ubuntu Linux 14 Community Support and Information 14 Documentation 17 Commercial Support for Ubuntu Linux 18 Getting More Information About Ubuntu 19 Summary 20 Chapter 2: Installing Ubuntu 21 Getting a 64-bit or PPC Desktop CD 22 Booting the Desktop CD 22 Installing Ubuntu Linux from the Desktop CD 24 Booting Ubuntu Linux 33 Booting Ubuntu Linux an Dual-Boot Systems 33 The First Time You Boot Ubuntu Linux 34 Test-Driving Ubuntu Linux 34 Expioring the Desktop CD's Examples Folder 34 Accessing Your Hard Drive from the Desktop CD 36 Using Desktop CD Persistence 41 Copying Files to Other Machines Over a Network 43 Installing Windows Programs from the Desktop CD 43 Summary 45 ix Contents Chapter 3: Installing Ubuntu on Special-Purpose Systems 47 Overview of Dual-Boot Systems 48 Your Computer's Boot Process 48 Configuring a System for Dual-Booting 49 Repartitioning an Existing Disk 49 Getting a Different Install CD 58 Booting from a Server or Altemate -

LIFE Packages
LIFE packages Index Office automation Desktop Internet Server Web developpement Tele centers Emulation Health centers Graphics High Schools Utilities Teachers Multimedia Tertiary schools Programming Database Games Documentation Internet - Firefox - Browser - Epiphany - Nautilus - Ftp client - gFTP - Evolution - Mail client - Thunderbird - Internet messaging - Gaim - Gaim - IRC - XChat - Gaim - VoIP - Skype - Videomeeting - Gnome meeting - GnomeBittorent - P2P - aMule - Firefox - Download manager - d4x - Telnet - Telnet Web developpement - Quanta - Bluefish - HTML editor - Nvu - Any text editor - HTML galerie - Album - Web server - XAMPP - Collaborative publishing system - Spip Desktop - Gnome - Desktop - Kde - Xfce Graphics - Advanced image editor - The Gimp - KolourPaint - Simple image editor - gPaint - TuxPaint - CinePaint - Video editor - Kino - OpenOffice Draw - Vector vraphics editor - Inkscape - Dia - Diagram editor - Kivio - Electrical CAD - Electric - 3D modeller/render - Blender - CAD system - QCad Utilities - Calculator - gCalcTool - gEdit - gxEdit - Text editor - eMacs21 - Leafpad - Application finder - Xfce4-appfinder - Desktop search tool - Beagle - File explorer - Nautilus -Archive manager - File-Roller - Nautilus CD Burner - CD burner - K3B - GnomeBaker - Synaptic - System updates - apt-get - IPtables - Firewall - FireStarter - BackupPC - Backup - Amanda - gnome-terminal - Terminal - xTerm - xTerminal - Scanner - Xsane - Partition editor - gParted - Making image of disks - Partitimage - Mirroring over network - UDP Cast -

Emmanuelle Chaigneau and Angus Silver
Investigation of dendritic integration in spiny stellate cells of barrel cortex with 2-photon uncaging. E Chaigneau1 and RA Silver1 1. University College London, Department of Neuroscience, Physiology & Pharmacology, Gower street, London WC1E 6BT, United Kingdom Corresponding author: [email protected] Keywords: 2-photon microscopy, 2-photon photolysis, cortex Excitatory spiny neurons in layer 4 of somato-sensory exert a strong influence on transmission of information from the thalamus to the cortex [1] [2]. Their hyperpolarized resting potential [3] and relatively weak synaptic input [4] recorded in vivo raises the question of how they reach spike threshold. We have investigated how spiny stellate cells in barrel cortex integrate synaptic input by applying 2-photon uncaging in acute thalamocortical slices from P22-28 mice. To do this we patch loaded the cells with Alexa-594 and visualized the dendritic tree with 2-photon imaging. Layer 4 excitatory cells were identified on the basis of their location, anatomy and regular spiking firing properties. Different patterns of synaptic input onto the dendritic tree was mimicked at high spatiotemporal resolution by uncaging MNI-glutamate close to individual spines, while recording the membrane voltage through the somatic patch pipette. Under our experimental conditions, the resting potential of spiny stellate cells was -77 ± 7 mV (n = 52 cells). To ensure that the level of activation of synaptic glutamate receptors with photolysis was comparable to that during synaptic transmission, we first measured the quantal size of synaptic events which was -10 ± 2 pA (n = 4 cells). We then adjusted the photolysis laser power and duration so that the current evoked by uncaging MNI-glutamate on spines close to the cell soma, where dendritic filtering is minimized, matched the miniature current amplitude,. -

Install Gnome Software Center Arch
Install gnome software center arch Upstream URL: License(s): GPL2. Maintainers: Jan Steffens. Package Size: MB. Installed Size: Installed Size: MB. gnome-software will be available as a preview in It can install, remove applications on systems with PackageKit. It can install updates on Gnome software will not start / Applications & Desktop. A quick video on Gnome Software Center in Arch Linux. Gnome unstable repository. There is a component called Polkit that is used by many applications to request root permissions to do things (it can do so because it's a. GNOME Software on #archlinux with native PackageKit backend, and this is a gui for installing software, ala ubuntu software manager, but distro This is some kind of Ubuntu Software Centre, with comments and all that. Need help installing Gnome Software Center for Arch Linux? Here are some instructions: Click DOWNLOAD HERE in the menu. Download the file. Make the file. I had to install it with along with packagekit. This is what's missing to make Antergos *the* beginner-friendly Arch-based distro, or general So, it is not a bad idea for the “Gnome Software Center” to include by default. GNOME software software center graphic that we will find the default in future releases of Fedora in addition to being installed in Arch Linux Please help me to install GNOME Software on. GNOME Software Will Work On Arch Linux With PackageKit the Alpm/Pacman back-end for using this GNOME application to install and. From: Sriram Ramkrishna ; To: desktop-devel-list devel-list gnome org>; Subject: gnome- software/packagekit.