DOCSLIB.ORG

Mathematical Tools

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mathematical Tools Appendix Mathematical Tools Contents A.1 Some Vector Calculus Results.............................................................. 389 A.1.1 Cartesian Index Notation.......................................................... 389 A.1.2 Derivatives of Fundamental Solutions of Laplace’s Equation................... 392 A.1.3 The Divergence Theorem and Some Relevant Uses.............................. 393 A.1.4 Stokes’ Theorem and Some Relevant Uses....................................... 405 A.1.5 Change of Variables Theorem..................................................... 411 A.1.6 Field Quantities and Their Rate of Change....................................... 411 A.1.7 Time Differentiation of Spatial Integrals.......................................... 412 A.2 Useful Tools from Complex Analysis...................................................... 416 A.2.1 Basic Properties.................................................................... 417 A.2.2 The Cauchy Integral and Residue Theorem...................................... 420 A.2.3 Conformal Mapping............................................................... 425 A.2.4 The Joukowski and Kármán–Trefftz Airfoils..................................... 431 A.2.5 The Schwarz–Christoffel Transformation......................................... 436 A.3 Mathematical Results for the Infinitely-Thin Plate......................................... 443 A.3.1 Notes on an Important Factor...................................................... 443 A.3.2 Properties of Chebyshev Polynomials............................................. 444 A.3.3 Contour Integrals of Interest....................................................... 452 A.1 Some Vector Calculus Results This section provides a number of useful identities from vector calculus. A.1.1 Cartesian Index Notation Before we go any further, let’s review the rules of index notation, a useful tool in proving identities. The convention we use here is a stripped-down version of the actual convention, which, for example, distinguishes covariant and contravariant © Springer Nature Switzerland AG 2019 389 J. D. Eldredge, Mathematical Modeling of Unsteady Inviscid Flows, Interdisciplinary Applied Mathematics 50, https://doi.org/10.1007/978-3-030-18319-6 390 A Mathematical Tools components. But since we only will write the indexed expressions in a Cartesian coordinate system, we have no need for such distinctions and can therefore keep it simple. First, the rules: 1. If a given letter index appears only once in each term of an equation, it is called a free index and the equation holds for all possible values of the index. If this index is ‘relabeled’ with a new letter, it must be relabeled consistently in every term. 2. If a letter index appears exactly twice in a term, then summation over all possible values of the index is implied. Such an index is called a dummy index. This index can be relabeled with a different letter (as long as the new letter does not conflict with another index), without affecting the other terms in the equation. 3. No letter index may appear more than twice in a given term. Some examples help to demonstrate the application of these rules: • The equation a = b + c can be represented in component form as ai = bi + ci. This obviously implies that the equation holds for all values of the free index i (1, 2, 3 in three-dimensional space, or just 1 and 2 in the plane). It would be a violation of rule 1 to change this to ai = bi + cj ; however, it is perfectly okay to change it to aj = bj + cj . • The dot product of two vectors, a · b, can be represented as ai bi, which implies a1b1 + a2b2 + a3b3 by rule 2 (when the dummy index i extends over the range 1, 2, 3). This can be relabeled as aj bj , provided j does not already appear as a free index or another dummy index in the term. • Note that multiplication of components is commutative, as it is for any scalar quantities, so we can reorder the components within a term however we find convenient. Thus, ai bi = biai. • By rule 3, the expression ai bici is meaningless. For example, the vector expression a = (b · c)d may be represented in component form as ai = bj cj di.Onemayalso relabel the dummy index j with another letter, such as k,toformai = bk ck di, but cannot relabel it with the letter i. Such relabeling can often be helpful for proving identities. For example, expression ai bicj dj fk − ambmcl dl fk vanishes, which is only obvious once the dummy indices in the second term are replaced as follows: m → i and l → j. The components of higher-rank tensors have the same number of indices as their rank; for example, Aij are the 9 (4 in two dimensions) components of a rank-two tensor, A. There are two tensors of special significance. The first is the Kronecker delta, defined as follows: 1, i = j δij ·= (A.1) 0, i j Note that the Kronecker delta is symmetric with respect to its indices, δij = δji.It has the property of ‘picking off’ a single component of a vector, e.g., δijvj = vi.To see this clearly, write out the sum completely, when, for example, i = 2: δ2j vj = δ21v1 + δ22v2 + δ23v3. (A.2) A.1 Some Vector Calculus Results 391 Only the middle term survives, and is equal to v2. This makes it clear that the Kronecker delta just describes the components of the identity tensor, 1. This tensor is isotropic, which means its components are the same in every Cartesian coordinate system. The cross (or vector) product between two vectors, denoted vectorially by c = a×b, uses another special isotropic tensor, this time of rank 3, called the permutation symbol, ijk. This symbol has the definition ⎧ ⎪⎨ 1, if ijk is an even permutation of 123 ijk ·= −1, if ijk is an odd permutation of 123 (A.3) ⎪ ⎩ 0, if any of ijk are equal Note that, for any three values of i, j and k, ijk = jki = kij = −ikj = −kji = −jik. By this definition, the cross-product operation can be denoted in index notation as follows: The ith component of c is ci = ijkaj bk . (A.4) The easiest way to see how this gives the usual relationship between components in the cross product is to write it out in full. Note that j and k are dummy indices in this expression. For example, when i = 1, c1 = 111a1b1 + 112a1b2 + 113a1b3 + 121a2b1 + 122a2b2 + 123a2b3 + 131a3b1 + 132a3b2 + 133a3b3. (A.5) By the definition of the permutation symbol, only the sixth and the eighth terms in this expression survive, and the result simplifies considerably to c1 = a2b3 − a3b2, as expected. A very useful relationship between the Kronecker delta and the permutation symbol is ijkklm = δilδjm − δimδjl. (A.6) This relationship holds in both two and three dimensions, and is generally used to derive identities involving two cross products: for example, a ×(b × c) = (a · c)b − (a · b)c. In two dimensions, it is often used with at least one of the three vectors or vector operators oriented in the out-of-plane direction. In such cases, one must take care to keep track of the range of each of the indices in (A.6). The reader is invited to use index notation to prove the following useful identity for two differentiable vector fields, a and b: ∇×(a × b) = ∇·(ba)−∇·(ab) = a(∇ · b)−b(∇ · a) + b ·∇a − a ·∇b. (A.7) 392 A Mathematical Tools A.1.2 Derivatives of Fundamental Solutions of Laplace’s Equation We can use index notation to develop some useful results concerning the derivatives of the distance r (or its inverse) from the origin to some point at x. First, note that we can write the square of this distance, in any dimension, as r2 = |x|2 = xk xk , where k is a dummy index. The most basic result we need in this context is ∂xi = δij. (A.8) ∂xj In other words, the derivative of a coordinate with respect to another coordinate is either 0 if their corresponding axes are different, or 1 if their axes are the same. Then, we can easily obtain the following: ∂r2 ∂ ∂xk = (xk xk ) = 2xk = 2xk δki = 2xi . (A.9) ∂xi ∂xi ∂xi But we can also use the product rule on this derivative, ∂r2 ∂r = 2r . (A.10) ∂xi ∂xi Combining these two results, we get the very useful identity ∂r xi = . (A.11) ∂xi r The right-hand side comprises the components of a unit vector from the origin toward the point. All of our other results in this discussion make use of (A.11) and the chain rule. For example, in two dimensional contexts, the fundamental solutions of Laplace’s equation in external regions are log r and its derivatives, so it is helpful to calculate a few of these: ∂ 1 ∂r xi (log r) = = , (A.12) ∂xi r ∂xi r2 followed by ∂2 ∂ xj δij 2xi xj (log r) = = − , (A.13) ∂xi ∂xj ∂xi r2 r2 r4 and ∂3 ∂ δjk 2xj xk 2xiδjk 2xj δki 2xk δij 8xi xj xk (log r) = − = − − − + . ∂xi ∂xj ∂xk ∂xi r2 r4 r4 r4 r4 r6 (A.14) Analogously, in three dimensions, 1/r and its derivatives form the fundamental solutions, so we calculate the first few of these: A.1 Some Vector Calculus Results 393 Fig. A.1 Schematic of a volume V and enclosing surface S ∂ 1 1 ∂r xi = − = − , (A.15) ∂xi r r2 ∂xi r3 and then, ∂2 1 ∂ xj δij 3xi xj = − = − + , (A.16) ∂xi ∂xj r ∂xi r3 r3 r5 and again, ∂3 1 ∂ δjk 3xj xk 3xiδjk 3xj δki 3xk δij 15xi xj xk = − + = + + − . ∂xi ∂xj ∂xk r ∂xi r3 r5 r5 r5 r5 r5 (A.17) A.1.3 The Divergence Theorem and Some Relevant Uses Consider a volume V and an enclosing surface S with outward unit normal n, as depicted in Fig. A.1. The divergence theorem allows us to relate integrals over V, involving some differentiable field quantity defined over that volume, to fluxes through the enclosing surface. This is an extremely powerful tool. The Generalized Divergence Theorem Though we are used to thinking of the divergence theorem applied to vector fields, in the most general form of the divergence theorem this field quantity is a tensor field of any rank.
Load more

Recommended publications
  • On the Spectrum of Volume Integral Operators in Acoustic Scattering M Costabel
    On the Spectrum of Volume Integral Operators in Acoustic Scattering M Costabel To cite this version: M Costabel. On the Spectrum of Volume Integral Operators in Acoustic Scattering. C. Constanda, A. Kirsch. Integral Methods in Science and Engineering, Birkhäuser, pp.119-127, 2015, 978-3-319- 16726-8. 10.1007/978-3-319-16727-5_11. hal-01098834v2 HAL Id: hal-01098834 https://hal.archives-ouvertes.fr/hal-01098834v2 Submitted on 20 Apr 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 1 On the Spectrum of Volume Integral Operators in Acoustic Scattering M. Costabel IRMAR, Université de Rennes 1, France; [email protected] 1.1 Volume Integral Equations in Acoustic Scattering Volume integral equations have been used as a theoretical tool in scattering theory for a long time. A classical application is an existence proof for the scattering problem based on the theory of Fredholm integral equations. This approach is described for acoustic and electromagnetic scattering in the books by Colton and Kress [CoKr83, CoKr98] where volume integral equations ap- pear under the name “Lippmann-Schwinger equations”. In electromagnetic scattering by penetrable objects, the volume integral equation (VIE) method has also been used for numerical computations.
    [Show full text]
  • Vector Calculus and Multiple Integrals Rob Fender, HT 2018
    Vector Calculus and Multiple Integrals Rob Fender, HT 2018 COURSE SYNOPSIS, RECOMMENDED BOOKS Course syllabus (on which exams are based): Double integrals and their evaluation by repeated integration in Cartesian, plane polar and other specified coordinate systems. Jacobians. Line, surface and volume integrals, evaluation by change of variables (Cartesian, plane polar, spherical polar coordinates and cylindrical coordinates only unless the transformation to be used is specified). Integrals around closed curves and exact differentials. Scalar and vector fields. The operations of grad, div and curl and understanding and use of identities involving these. The statements of the theorems of Gauss and Stokes with simple applications. Conservative fields. Recommended Books: Mathematical Methods for Physics and Engineering (Riley, Hobson and Bence) This book is lazily referred to as “Riley” throughout these notes (sorry, Drs H and B) You will all have this book, and it covers all of the maths of this course. However it is rather terse at times and you will benefit from looking at one or both of these: Introduction to Electrodynamics (Griffiths) You will buy this next year if you haven’t already, and the chapter on vector calculus is very clear Div grad curl and all that (Schey) A nice discussion of the subject, although topics are ordered differently to most courses NB: the latest version of this book uses the opposite convention to polar coordinates to this course (and indeed most of physics), but older versions can often be found in libraries 1 Week One A review of vectors, rotation of coordinate systems, vector vs scalar fields, integrals in more than one variable, first steps in vector differentiation, the Frenet-Serret coordinate system Lecture 1 Vectors A vector has direction and magnitude and is written in these notes in bold e.g.
    [Show full text]
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
    AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43.
    [Show full text]
  • Mathematical Theorems
    Appendix A Mathematical Theorems The mathematical theorems needed in order to derive the governing model equations are defined in this appendix. A.1 Transport Theorem for a Single Phase Region The transport theorem is employed deriving the conservation equations in continuum mechanics. The mathematical statement is sometimes attributed to, or named in honor of, the German Mathematician Gottfried Wilhelm Leibnitz (1646–1716) and the British fluid dynamics engineer Osborne Reynolds (1842–1912) due to their work and con- tributions related to the theorem. Hence it follows that the transport theorem, or alternate forms of the theorem, may be named the Leibnitz theorem in mathematics and Reynolds transport theorem in mechanics. In a customary interpretation the Reynolds transport theorem provides the link between the system and control volume representations, while the Leibnitz’s theorem is a three dimensional version of the integral rule for differentiation of an integral. There are several notations used for the transport theorem and there are numerous forms and corollaries. A.1.1 Leibnitz’s Rule The Leibnitz’s integral rule gives a formula for differentiation of an integral whose limits are functions of the differential variable [7, 8, 22, 23, 45, 55, 79, 94, 99]. The formula is also known as differentiation under the integral sign. H. A. Jakobsen, Chemical Reactor Modeling, DOI: 10.1007/978-3-319-05092-8, 1361 © Springer International Publishing Switzerland 2014 1362 Appendix A: Mathematical Theorems b(t) b(t) d ∂f (t, x) db da f (t, x) dx = dx + f (t, b) − f (t, a) (A.1) dt ∂t dt dt a(t) a(t) The first term on the RHS gives the change in the integral because the function itself is changing with time, the second term accounts for the gain in area as the upper limit is moved in the positive axis direction, and the third term accounts for the loss in area as the lower limit is moved.
    [Show full text]
  • An Introduction to Fluid Mechanics: Supplemental Web Appendices
    An Introduction to Fluid Mechanics: Supplemental Web Appendices Faith A. Morrison Professor of Chemical Engineering Michigan Technological University November 5, 2013 2 c 2013 Faith A. Morrison, all rights reserved. Appendix C Supplemental Mathematics Appendix C.1 Multidimensional Derivatives In section 1.3.1.1 we reviewed the basics of the derivative of single-variable functions. The same concepts may be applied to multivariable functions, leading to the definition of the partial derivative. Consider the multivariable function f(x, y). An example of such a function would be elevations above sea level of a geographic region or the concentration of a chemical on a flat surface. To quantify how this function changes with position, we consider two nearby points, f(x, y) and f(x + ∆x, y + ∆y) (Figure C.1). We will also refer to these two points as f x,y (f evaluated at the point (x, y)) and f . | |x+∆x,y+∆y In a two-dimensional function, the “rate of change” is a more complex concept than in a one-dimensional function. For a one-dimensional function, the rate of change of the function f with respect to the variable x was identified with the change in f divided by the change in x, quantified in the derivative, df/dx (see Figure 1.26). For a two-dimensional function, when speaking of the rate of change, we must also specify the direction in which we are interested. For example, if the function we are considering is elevation and we are standing near the edge of a cliff, the rate of change of the elevation in the direction over the cliff is steep, while the rate of change of the elevation in the opposite direction is much more gradual.
    [Show full text]
  • Multivariable and Vector Calculus
    Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space.
    [Show full text]
  • Lecture 33 Classical Integration Theorems in the Plane
    Lecture 33 Classical Integration Theorems in the Plane In this section, we present two very important results on integration over closed curves in the plane, namely, Green’s Theorem and the Divergence Theorem, as a prelude to their important counterparts in R3 involving surface integrals. Green’s Theorem in the Plane (Relevant section from Stewart, Calculus, Early Transcendentals, Sixth Edition: 16.4) 2 1 Let F(x,y) = F1(x,y) i + F2(x,y) j be a vector field in R . Let C be a simple closed (piecewise C ) curve in R2 that encloses a simply connected (i.e., “no holes”) region D ⊂ R. Also assume that the ∂F ∂F partial derivatives 2 and 1 exist at all points (x,y) ∈ D. Then, ∂x ∂y ∂F ∂F F · dr = 2 − 1 dA, (1) IC Z ZD ∂x ∂y where the line integration is performed over C in a counterclockwise direction, with D lying to the left of the path. Note: 1. The integral on the left is a line integral – the circulation of the vector field F over the closed curve C. 2. The integral on the right is a double integral over the region D enclosed by C. Special case: If ∂F ∂F 2 = 1 , (2) ∂x ∂y for all points (x,y) ∈ D, then the integrand in the double integral of Eq. (1) is zero, implying that the circulation integral F · dr is zero. IC We’ve seen this situation before: Recall that the above equality condition for the partial derivatives is the condition for F to be conservative.
    [Show full text]
  • Math 132 Exam 1 Solutions
    Math 132, Exam 1, Fall 2017 Solutions You may have a single 3x5 notecard (two-sided) with any notes you like. Otherwise you should have only your pencils/pens and eraser. No calculators are allowed. No consultation with any other person or source of information (physical or electronic) is allowed during the exam. All electronic devices should be turned off. Part I of the exam contains questions 1-14 (multiple choice questions, 5 points each) and true/false questions 15-19 (1 point each). Your answers in Part I should be recorded on the “scantron” card that is provided. If you need to make a change on your answer card, be sure your original answer is completely erased. If your card is damaged, ask one of the proctors for a replacement card. Only the answers marked on the card will be scored. Part II has 3 “written response” questions worth a total of 25 points. Your answers should be written on the pages of the exam booklet. Please write clearly so the grader can read them. When a calculation or explanation is required, your work should include enough detail to make clear how you arrived at your answer. A correct numeric answer with sufficient supporting work may not receive full credit. Part I 1. Suppose that If and , what is ? A) B) C) D) E) F) G) H) I) J) so So and therefore 2. What are all the value(s) of that make the following equation true? A) B) C) D) E) F) G) H) I) J) all values of make the equation true For any , 3.
    [Show full text]
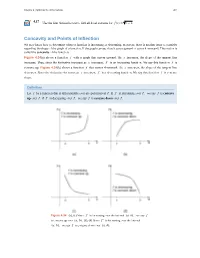
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Introduction to Theoretical Methods Example
    Differentiation of integrals and Leibniz rule • We are interested in solving problems of the type d Z v(x) f (x; t)dt dx u(x) • Notice in addition to the limits depending on x, the function f (x; t) also depends on x • First lets take the case where the limits are constants (u(x) = b and v(x) = a) • In most instances we can take the derivative inside the integral (as a partial derivative) d Z b Z b @f (x; t) f (x; t)dt = dt dx a a @x Patrick K. Schelling Introduction to Theoretical Methods Example R 1 n −kt2 • Find 0 t e dt for n odd • First solve for n = 1, 1 Z 2 I = te−kt dt 0 • Use u = kt2 and du = 2ktdt, so 1 1 Z 2 1 Z 1 I = te−kt dt = e−udu = 0 2k 0 2k dI R 1 3 −kt2 1 • Next notice dk = 0 −t e dt = − 2k2 • We can take successive derivatives with respect to k, so we find Z 1 2n+1 −kt2 n! t e dt = n+1 0 2k Patrick K. Schelling Introduction to Theoretical Methods Another example... the even n case R 1 n −kt2 • The even n case can be done of 0 t e dt • Take for I in this case (writing in terms of x instead of t) 1 Z 2 I = e−kx dx −∞ • We can write for I 2, 1 1 Z Z 2 2 I 2 = e−k(x +y )dxdy −∞ −∞ • Make a change of variables to polar coordinates, x = r cos θ, y = r sin θ, and x2 + y 2 = r 2 • The dxdy in the integrand becomes rdrdθ (we will explore this more carefully in the next chapter) Patrick K.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]