DOCSLIB.ORG

Matrix Calculus

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Matrix Calculus Appendix D Matrix Calculus From too much study, and from extreme passion, cometh madnesse. Isaac Newton [205, §5] − D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient of a differentiable real function f(x) : RK R with respect to its vector argument is defined uniquely in terms of partial derivatives→ ∂f(x) ∂x1 ∂f(x) , ∂x2 RK f(x) . (2053) ∇ . ∈ . ∂f(x) ∂xK while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian; 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂x1 ∂x1∂x2 ··· ∂x1∂xK 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 2 K f(x) , ∂x2∂x1 ∂x2 ··· ∂x2∂xK S (2054) ∇ . ∈ . .. 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂xK ∂x1 ∂xK ∂x2 ∂x ··· K interpreted ∂f(x) ∂f(x) 2 ∂ ∂ 2 ∂ f(x) ∂x1 ∂x2 ∂ f(x) = = = (2055) ∂x1∂x2 ³∂x2 ´ ³∂x1 ´ ∂x2∂x1 Dattorro, Convex Optimization Euclidean Distance Geometry, Mεβoo, 2005, v2020.02.29. 599 600 APPENDIX D. MATRIX CALCULUS The gradient of vector-valued function v(x) : R RN on real domain is a row vector → v(x) , ∂v1(x) ∂v2(x) ∂vN (x) RN (2056) ∇ ∂x ∂x ··· ∂x ∈ h i while the second-order gradient is 2 2 2 2 , ∂ v1(x) ∂ v2(x) ∂ vN (x) RN v(x) 2 2 2 (2057) ∇ ∂x ∂x ··· ∂x ∈ h i Gradient of vector-valued function h(x) : RK RN on vector domain is → ∂h1(x) ∂h2(x) ∂hN (x) ∂x1 ∂x1 ··· ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) h(x) , ∂x2 ∂x2 ··· ∂x2 ∇ . . (2058) ∂h1(x) ∂h2(x) ∂hN (x) ∂xK ∂xK ··· ∂xK K×N = [ h (x) h (x) hN (x) ] R ∇ 1 ∇ 2 ··· ∇ ∈ while the second-order gradient has a three-dimensional written representation dubbed cubix ;D.1 ∂h1(x) ∂h2(x) ∂hN (x) ∇ ∂x1 ∇ ∂x1 ··· ∇ ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) 2h(x) , ∇ ∂x2 ∇ ∂x2 ··· ∇ ∂x2 ∇ . . (2059) ∂h1(x) ∂h2(x) ∂hN (x) ∇ ∂xK ∇ ∂xK ··· ∇ ∂xK 2 2 2 K×N×K = h (x) h (x) hN (x) R ∇ 1 ∇ 2 ··· ∇ ∈ where the gradient of each£ real entry is with respect to vector¤ x as in (2053). The gradient of real function g(X) : RK×L R on matrix domain is → ∂g(X) ∂g(X) ∂g(X) ∂X11 ∂X12 ··· ∂X1L ∂g(X) ∂g(X) ∂g(X) K×L g(X) , ∂X21 ∂X22 ··· ∂X2L R ∇ . ∈ . ∂g(X) ∂g(X) ∂g(X) ∂XK1 ∂XK2 ··· ∂XKL (2060) g(X) ∇X(:,1) £ X(:,2) g(X) K L = R ×1× ∇ . .. ∈ g(X) ∇X(:,L) ¤ where gradient is with respect to the ith column of X . The strange appearance of ∇X(:, i) (2060) in RK×1×L is meant to suggest a third dimension perpendicular to the page (not D.1The word matrix comes from the Latin for womb ; related to the prefix matri- derived from mater meaning mother. D.1. GRADIENT, DIRECTIONAL DERIVATIVE, TAYLOR SERIES 601 a diagonal matrix). The second-order gradient has representation ∂g(X) ∂g(X) ∂g(X) ∇ ∂X11 ∇ ∂X12 ··· ∇ ∂X1L ∂g(X) ∂g(X) ∂g(X) 2 K×L×K×L g(X) , ∇ ∂X21 ∇ ∂X22 ··· ∇ ∂X2L R ∇ . ∈ . ∂g(X) ∂g(X) ∂g(X) ∇ ∂XK1 ∇ ∂XK2 ··· ∇ ∂XKL (2061) g(X) ∇∇X(:,1) £ X(:,2) g(X) K L K L = R ×1× × × ∇∇ . .. ∈ g(X) ∇∇X(:,L) where the gradient is with respect to matrix X . ¤ Gradient of vector-valued∇ function g(X) : RK×L RN on matrix domain is a cubix → g (X) g (X) gN (X) ∇X(:,1) 1 ∇X(:,1) 2 ··· ∇X(:,1) £ X(:,2) g1(X) X(:,2) g2(X) X(:,2) gN (X) g(X) , ∇ . ∇ . ··· ∇ . ∇ .. .. .. (2062) g (X) g (X) gN (X) ∇X(:,L) 1 ∇X(:,L) 2 ··· ∇X(:,L) ¤ K×N×L = [ g (X) g (X) gN (X) ] R ∇ 1 ∇ 2 ··· ∇ ∈ while the second-order gradient has a five-dimensional representation; g (X) g (X) gN (X) ∇∇X(:,1) 1 ∇∇X(:,1) 2 · · · ∇∇X(:,1) £ X(:,2) g1(X) X(:,2) g2(X) X(:,2) gN (X) 2g(X) , ∇∇ . ∇∇ . · · · ∇∇ . ∇ .. .. .. (2063) g (X) g (X) gN (X) ∇∇X(:,L) 1 ∇∇X(:,L) 2 · · · ∇∇X(:,L) ¤ 2 2 2 K×N×L×K×L = g (X) g (X) gN (X) R ∇ 1 ∇ 2 ··· ∇ ∈ The£ gradient of matrix-valued function g¤(X) : RK×L RM×N on matrix domain has a four-dimensional representation called quartix (fourth-order→ tensor) g (X) g (X) g N (X) ∇ 11 ∇ 12 ··· ∇ 1 g (X) g (X) g N (X) M×N×K×L g(X) , ∇ 21 ∇ 22 ··· ∇ 2 R (2064) ∇ . ∈ . gM1(X) gM2(X) gMN (X) ∇ ∇ ··· ∇ while the second-order gradient has a six-dimensional representation 2 2 2 g (X) g (X) g N (X) ∇ 11 ∇ 12 ··· ∇ 1 2 2 2 g (X) g (X) g N (X) M×N×K×L×K×L 2g(X) , ∇ 21 ∇ 22 ··· ∇ 2 R (2065) ∇ . ∈ . 2 2 2 gM1(X) gM2(X) gMN (X) ∇ ∇ ··· ∇ and so on. 602 APPENDIX D. MATRIX CALCULUS D.1.2 Product rules for matrix-functions Given dimensionally compatible matrix-valued functions of matrix variable f(X) and g(X) T X f(X) g(X) = X (f) g + X (g) f (2066) ∇ ∇ ∇ while [65, §8.3] [420] ¡ ¢ T T T X tr f(X) g(X) = X tr f(X) g(Z) + tr g(X) f(Z) (2067) ∇ ∇ Z←X ³ ´¯ ¡ ¢ ¡ ¢ ¡ ¢ ¯ These expressions implicitly apply as well to scalar-, vector-, or matrix-valued¯ functions of scalar, vector, or matrix arguments. D.1.2.0.1 Example. Cubix. 2 2 2 2 2 2 Suppose f(X) : R × R = XTa and g(X) : R × R = Xb . We wish to find → → T T 2 X f(X) g(X) = X a X b (2068) ∇ ∇ using the product rule. Formula (¡2066) calls for¢ T 2 T T X a X b = X (X a) Xb + X (Xb) X a (2069) ∇ ∇ ∇ Consider the first of the two terms: T X (f) g = X (X a) Xb ∇ ∇ (2070) = (XTa) (XTa) Xb ∇ 1 ∇ 2 2 2 2 The gradient of XTa forms a cubix in£ R × × ; a.k.a, third-order¤ tensor. T T ∂(X a)1 ∂(X a)2 (2071) ∂X11 ∂X11 Â Â Â Â Â Â Â Â Â Â Â Â T T ∂(X a)1 ∂(X a)2 ∂X12 ∂X12 (Xb)1 T 2×1×2 X (X a) Xb = R T T ∇ ∂(X a)1 ∂(X a)2 ∈ ∂X21 ∂X21 (Xb)2 Â Â Â Â Â Â Â Â Â Â Â Â T T ∂(X a)1 ∂(X a)2 ∂X22 ∂X22 Because gradient of the product (2068) requires total change with respect to change in each entry of matrix X , the Xb vector must make an inner product with each vector in that second dimension of the cubix indicated by dotted line segments; a1 0 T 0 a1 b1X11 + b2X12 2×1×2 X (X a) Xb = R ∇ a 0 b1X21 + b2X22 ∈ 2 · ¸ 0 a2 (2072) a (b X + b X ) a (b X + b X ) 2 2 = 1 1 11 2 12 1 1 21 2 22 R × a2(b1X11 + b2X12) a2(b1X21 + b2X22) ∈ · ¸ = abTXT where the cubix appears as a complete 2 2 2 matrix. In like manner for the second × × term X (g) f ∇ D.1. GRADIENT, DIRECTIONAL DERIVATIVE, TAYLOR SERIES 603 b1 0 T b2 0 X11a1 + X21a2 2×1×2 X (Xb) X a = R ∇ 0 b X12a1 + X22a2 ∈ 1 · ¸ (2073) 0 b2 2 2 = XTabT R × The solution ∈ T 2 T T T T X a X b = ab X + X ab (2074) ∇ can be found from Table D.2.1 or verified using (2067). 2 D.1.2.1 Kronecker product A partial remedy for venturing into hyperdimensional matrix representations, such as the cubix or quartix, is to first vectorize matrices as in (39). This device gives rise to the Kronecker product of matrices ; a.k.a, tensor product (kron() in Matlab). ⊗ Although its definition sees reversal in the literature, [434, §2.1] Kronecker product is not commutative (B A = A B). We adopt the definition: for A Rm×n and B Rp×q ⊗ 6 ⊗ ∈ ∈ B A B A B qA 11 12 ··· 1 B A B A B qA 21 22 2 pm qn B A , . ··· . R × (2075) ⊗ . ∈ Bp A Bp A BpqA 1 2 ··· for which A 1 = 1 A = A (real unity acts like Identity). One advantage⊗ to⊗ vectorization is existence of the traditional two-dimensional matrix representation (second-order tensor) for the second-order gradient of a real function with n×n § respect to a vectorized matrix. From §A.1.1 no.36 ( D.2.1) for square A,B R , for ∈ § example [220, §5.2] [15, 3] 2 2 2 tr(AXBXT) = 2 vec(X)T(BT A) vec X = B AT + BT A Rn × n (2076) ∇vec X ∇vec X ⊗ ⊗ ⊗ ∈ To disadvantage is a large new but known set of algebraic rules (§A.1.1) and the fact that its mere use does not generally guarantee two-dimensional matrix representation of gradients. Another application of the Kronecker product is to reverse order of appearance in a matrix product: Suppose we wish to weight the columns of a matrix S RM×N , for ∈ example, by respective entries wi from the main diagonal in w1 0 . N W , .. S (2077) ∈ 0 wN A conventional means for accomplishing column weighting is to multiply S by diagonal matrix W on the right side: w1 0 . M×N S W = S .. = S(: , 1)w1 S(: , N)wN R (2078) ··· ∈ 0 w N £ ¤ To reverse product order such that diagonal matrix W instead appears to the left of S : for I SM (Law) ∈ S(: , 1) 0 0 .
Load more

Recommended publications
  • The Directional Derivative the Derivative of a Real Valued Function (Scalar field) with Respect to a Vector
    Math 253 The Directional Derivative The derivative of a real valued function (scalar field) with respect to a vector. f(x + h) f(x) What is the vector space analog to the usual derivative in one variable? f 0(x) = lim − ? h 0 h ! x -2 0 2 5 Suppose f is a real valued function (a mapping f : Rn R). ! (e.g. f(x; y) = x2 y2). − 0 Unlike the case with plane figures, functions grow in a variety of z ways at each point on a surface (or n{dimensional structure). We'll be interested in examining the way (f) changes as we move -5 from a point X~ to a nearby point in a particular direction. -2 0 y 2 Figure 1: f(x; y) = x2 y2 − The Directional Derivative x -2 0 2 5 We'll be interested in examining the way (f) changes as we move ~ in a particular direction 0 from a point X to a nearby point . z -5 -2 0 y 2 Figure 2: f(x; y) = x2 y2 − y If we give the direction by using a second vector, say ~u, then for →u X→ + h any real number h, the vector X~ + h~u represents a change in X→ position from X~ along a line through X~ parallel to ~u. →u →u h x Figure 3: Change in position along line parallel to ~u The Directional Derivative x -2 0 2 5 We'll be interested in examining the way (f) changes as we move ~ in a particular direction 0 from a point X to a nearby point .
    [Show full text]
  • Mathematics for Dynamicists - Lecture Notes Thomas Michelitsch
    Mathematics for Dynamicists - Lecture Notes Thomas Michelitsch To cite this version: Thomas Michelitsch. Mathematics for Dynamicists - Lecture Notes. Doctoral. Mathematics for Dynamicists, France. 2006. cel-01128826 HAL Id: cel-01128826 https://hal.archives-ouvertes.fr/cel-01128826 Submitted on 10 Mar 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Mathematics for Dynamicists Lecture Notes c 2004-2006 Thomas Michael Michelitsch1 Department of Civil and Structural Engineering The University of Sheffield Sheffield, UK 1Present address : http://www.dalembert.upmc.fr/home/michelitsch/ . Dedicated to the memory of my parents Michael and Hildegard Michelitsch Handout Manuscript with Fractal Cover Picture by Michael Michelitsch https://www.flickr.com/photos/michelitsch/sets/72157601230117490 1 Contents Preface 1 Part I 1.1 Binomial Theorem 1.2 Derivatives, Integrals and Taylor Series 1.3 Elementary Functions 1.4 Complex Numbers: Cartesian and Polar Representation 1.5 Sequences, Series, Integrals and Power-Series 1.6 Polynomials and Partial Fractions
    [Show full text]
  • Training Autoencoders by Alternating Minimization
    Under review as a conference paper at ICLR 2018 TRAINING AUTOENCODERS BY ALTERNATING MINI- MIZATION Anonymous authors Paper under double-blind review ABSTRACT We present DANTE, a novel method for training neural networks, in particular autoencoders, using the alternating minimization principle. DANTE provides a distinct perspective in lieu of traditional gradient-based backpropagation techniques commonly used to train deep networks. It utilizes an adaptation of quasi-convex optimization techniques to cast autoencoder training as a bi-quasi-convex optimiza- tion problem. We show that for autoencoder configurations with both differentiable (e.g. sigmoid) and non-differentiable (e.g. ReLU) activation functions, we can perform the alternations very effectively. DANTE effortlessly extends to networks with multiple hidden layers and varying network configurations. In experiments on standard datasets, autoencoders trained using the proposed method were found to be very promising and competitive to traditional backpropagation techniques, both in terms of quality of solution, as well as training speed. 1 INTRODUCTION For much of the recent march of deep learning, gradient-based backpropagation methods, e.g. Stochastic Gradient Descent (SGD) and its variants, have been the mainstay of practitioners. The use of these methods, especially on vast amounts of data, has led to unprecedented progress in several areas of artificial intelligence. On one hand, the intense focus on these techniques has led to an intimate understanding of hardware requirements and code optimizations needed to execute these routines on large datasets in a scalable manner. Today, myriad off-the-shelf and highly optimized packages exist that can churn reasonably large datasets on GPU architectures with relatively mild human involvement and little bootstrap effort.
    [Show full text]
  • A Brief but Important Note on the Product Rule
    A brief but important note on the product rule Peter Merrotsy The University of Western Australia [email protected] The product rule in the Australian Curriculum he product rule refers to the derivative of the product of two functions Texpressed in terms of the functions and their derivatives. This result first naturally appears in the subject Mathematical Methods in the senior secondary Australian Curriculum (Australian Curriculum, Assessment and Reporting Authority [ACARA], n.d.b). In the curriculum content, it is mentioned by name only (Unit 3, Topic 1, ACMMM104). Elsewhere (Glossary, p. 6), detail is given in the form: If h(x) = f(x) g(x), then h'(x) = f(x) g'(x) + f '(x) g(x) (1) or, in Leibniz notation, d dv du ()u v = u + v (2) dx dx dx presupposing, of course, that both u and v are functions of x. In the Australian Capital Territory (ACT Board of Senior Secondary Studies, 2014, pp. 28, 43), Tasmania (Tasmanian Qualifications Authority, 2014, p. 21) and Western Australia (School Curriculum and Standards Authority, 2014, WACE, Mathematical Methods Year 12, pp. 9, 22), these statements of the Australian Senior Mathematics Journal vol. 30 no. 2 product rule have been adopted without further commentary. Elsewhere, there are varying attempts at elaboration. The SACE Board of South Australia (2015, p. 29) refers simply to “differentiating functions of the form , using the product rule.” In Queensland (Queensland Studies Authority, 2008, p. 14), a slight shift in notation is suggested by referring to rules for differentiation, including: d []f (t)g(t) (product rule) (3) dt At first, the Victorian Curriculum and Assessment Authority (2015, p.
    [Show full text]
  • The Mean Value Theorem Math 120 Calculus I Fall 2015
    The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0.
    [Show full text]
  • AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
    AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43.
    [Show full text]
  • A Quotient Rule Integration by Parts Formula Jennifer Switkes ([email protected]), California State Polytechnic Univer- Sity, Pomona, CA 91768
    A Quotient Rule Integration by Parts Formula Jennifer Switkes ([email protected]), California State Polytechnic Univer- sity, Pomona, CA 91768 In a recent calculus course, I introduced the technique of Integration by Parts as an integration rule corresponding to the Product Rule for differentiation. I showed my students the standard derivation of the Integration by Parts formula as presented in [1]: By the Product Rule, if f (x) and g(x) are differentiable functions, then d f (x)g(x) = f (x)g(x) + g(x) f (x). dx Integrating on both sides of this equation, f (x)g(x) + g(x) f (x) dx = f (x)g(x), which may be rearranged to obtain f (x)g(x) dx = f (x)g(x) − g(x) f (x) dx. Letting U = f (x) and V = g(x) and observing that dU = f (x) dx and dV = g(x) dx, we obtain the familiar Integration by Parts formula UdV= UV − VdU. (1) My student Victor asked if we could do a similar thing with the Quotient Rule. While the other students thought this was a crazy idea, I was intrigued. Below, I derive a Quotient Rule Integration by Parts formula, apply the resulting integration formula to an example, and discuss reasons why this formula does not appear in calculus texts. By the Quotient Rule, if f (x) and g(x) are differentiable functions, then ( ) ( ) ( ) − ( ) ( ) d f x = g x f x f x g x . dx g(x) [g(x)]2 Integrating both sides of this equation, we get f (x) g(x) f (x) − f (x)g(x) = dx.
    [Show full text]
  • Notes for Math 136: Review of Calculus
    Notes for Math 136: Review of Calculus Gyu Eun Lee These notes were written for my personal use for teaching purposes for the course Math 136 running in the Spring of 2016 at UCLA. They are also intended for use as a general calculus reference for this course. In these notes we will briefly review the results of the calculus of several variables most frequently used in partial differential equations. The selection of topics is inspired by the list of topics given by Strauss at the end of section 1.1, but we will not cover everything. Certain topics are covered in the Appendix to the textbook, and we will not deal with them here. The results of single-variable calculus are assumed to be familiar. Practicality, not rigor, is the aim. This document will be updated throughout the quarter as we encounter material involving additional topics. We will focus on functions of two real variables, u = u(x;t). Most definitions and results listed will have generalizations to higher numbers of variables, and we hope the generalizations will be reasonably straightforward to the reader if they become necessary. Occasionally (notably for the chain rule in its many forms) it will be convenient to work with functions of an arbitrary number of variables. We will be rather loose about the issues of differentiability and integrability: unless otherwise stated, we will assume all derivatives and integrals exist, and if we require it we will assume derivatives are continuous up to the required order. (This is also generally the assumption in Strauss.) 1 Differential calculus of several variables 1.1 Partial derivatives Given a scalar function u = u(x;t) of two variables, we may hold one of the variables constant and regard it as a function of one variable only: vx(t) = u(x;t) = wt(x): Then the partial derivatives of u with respect of x and with respect to t are defined as the familiar derivatives from single variable calculus: ¶u dv ¶u dw = x ; = t : ¶t dt ¶x dx c 2016, Gyu Eun Lee.
    [Show full text]
  • Multivariable and Vector Calculus
    Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space.
    [Show full text]
  • Deep Learning Based Computer Generated Face Identification Using
    applied sciences Article Deep Learning Based Computer Generated Face Identification Using Convolutional Neural Network L. Minh Dang 1, Syed Ibrahim Hassan 1, Suhyeon Im 1, Jaecheol Lee 2, Sujin Lee 1 and Hyeonjoon Moon 1,* 1 Department of Computer Science and Engineering, Sejong University, Seoul 143-747, Korea; [email protected] (L.M.D.); [email protected] (S.I.H.); [email protected] (S.I.); [email protected] (S.L.) 2 Department of Information Communication Engineering, Sungkyul University, Seoul 143-747, Korea; [email protected] * Correspondence: [email protected] Received: 30 October 2018; Accepted: 10 December 2018; Published: 13 December 2018 Abstract: Generative adversarial networks (GANs) describe an emerging generative model which has made impressive progress in the last few years in generating photorealistic facial images. As the result, it has become more and more difficult to differentiate between computer-generated and real face images, even with the human’s eyes. If the generated images are used with the intent to mislead and deceive readers, it would probably cause severe ethical, moral, and legal issues. Moreover, it is challenging to collect a dataset for computer-generated face identification that is large enough for research purposes because the number of realistic computer-generated images is still limited and scattered on the internet. Thus, a development of a novel decision support system for analyzing and detecting computer-generated face images generated by the GAN network is crucial. In this paper, we propose a customized convolutional neural network, namely CGFace, which is specifically designed for the computer-generated face detection task by customizing the number of convolutional layers, so it performs well in detecting computer-generated face images.
    [Show full text]
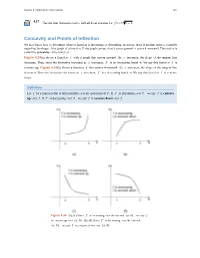
  • Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
    Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing.
    [Show full text]
  • Tensor Calculus and Differential Geometry
    Course Notes Tensor Calculus and Differential Geometry 2WAH0 Luc Florack March 10, 2021 Cover illustration: papyrus fragment from Euclid’s Elements of Geometry, Book II [8]. Contents Preface iii Notation 1 1 Prerequisites from Linear Algebra 3 2 Tensor Calculus 7 2.1 Vector Spaces and Bases . .7 2.2 Dual Vector Spaces and Dual Bases . .8 2.3 The Kronecker Tensor . 10 2.4 Inner Products . 11 2.5 Reciprocal Bases . 14 2.6 Bases, Dual Bases, Reciprocal Bases: Mutual Relations . 16 2.7 Examples of Vectors and Covectors . 17 2.8 Tensors . 18 2.8.1 Tensors in all Generality . 18 2.8.2 Tensors Subject to Symmetries . 22 2.8.3 Symmetry and Antisymmetry Preserving Product Operators . 24 2.8.4 Vector Spaces with an Oriented Volume . 31 2.8.5 Tensors on an Inner Product Space . 34 2.8.6 Tensor Transformations . 36 2.8.6.1 “Absolute Tensors” . 37 CONTENTS i 2.8.6.2 “Relative Tensors” . 38 2.8.6.3 “Pseudo Tensors” . 41 2.8.7 Contractions . 43 2.9 The Hodge Star Operator . 43 3 Differential Geometry 47 3.1 Euclidean Space: Cartesian and Curvilinear Coordinates . 47 3.2 Differentiable Manifolds . 48 3.3 Tangent Vectors . 49 3.4 Tangent and Cotangent Bundle . 50 3.5 Exterior Derivative . 51 3.6 Affine Connection . 52 3.7 Lie Derivative . 55 3.8 Torsion . 55 3.9 Levi-Civita Connection . 56 3.10 Geodesics . 57 3.11 Curvature . 58 3.12 Push-Forward and Pull-Back . 59 3.13 Examples . 60 3.13.1 Polar Coordinates in the Euclidean Plane .
    [Show full text]