The Search for Orbital Decay in Hot Jupiters
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Cfa in the News ~ Week Ending 3 January 2010
Wolbach Library: CfA in the News ~ Week ending 3 January 2010 1. New social science research from G. Sonnert and co-researchers described, Science Letter, p40, Tuesday, January 5, 2010 2. 2009 in science and medicine, ROGER SCHLUETER, Belleville News Democrat (IL), Sunday, January 3, 2010 3. 'Science, celestial bodies have always inspired humankind', Staff Correspondent, Hindu (India), Tuesday, December 29, 2009 4. Why is Carpenter defending scientists?, The Morning Call, Morning Call (Allentown, PA), FIRST ed, pA25, Sunday, December 27, 2009 5. CORRECTIONS, OPINION BY RYAN FINLEY, ARIZONA DAILY STAR, Arizona Daily Star (AZ), FINAL ed, pA2, Saturday, December 19, 2009 6. We see a 'Super-Earth', TOM BEAL; TOM BEAL, ARIZONA DAILY STAR, Arizona Daily Star, (AZ), FINAL ed, pA1, Thursday, December 17, 2009 Record - 1 DIALOG(R) New social science research from G. Sonnert and co-researchers described, Science Letter, p40, Tuesday, January 5, 2010 TEXT: "In this paper we report on testing the 'rolen model' and 'opportunity-structure' hypotheses about the parents whom scientists mentioned as career influencers. According to the role-model hypothesis, the gender match between scientist and influencer is paramount (for example, women scientists would disproportionately often mention their mothers as career influencers)," scientists writing in the journal Social Studies of Science report (see also ). "According to the opportunity-structure hypothesis, the parent's educational level predicts his/her probability of being mentioned as a career influencer (that ism parents with higher educational levels would be more likely to be named). The examination of a sample of American scientists who had received prestigious postdoctoral fellowships resulted in rejecting the role-model hypothesis and corroborating the opportunity-structure hypothesis. -

Uniform Forward-Modeling Analysis of Ultracool Dwarfs. II. Atmospheric Properties of 55 Late-T Dwarfs
DRAFT VERSION MAY 13, 2021 Typeset using LATEX twocolumn style in AASTeX61 Uniform Forward-Modeling Analysis of Ultracool Dwarfs. II. Atmospheric Properties of 55 Late-T Dwarfs ZHOUJIAN ZHANG ( he), 1, 2 MICHAEL C. LIU,1 MARK S. MARLEY,3, 4 MICHAEL R. LINE,5 AND WILLIAM M. J. BEST6 1Institute for Astronomy, University of Hawaii at Manoa, Honolulu, HI 96822, USA 2Visiting Astronomer at the Infrared Telescope Facility, which is operated by the University of Hawaii under contract 80HQTR19D0030 with the National Aeronautics and Space Administration. 3NASA Ames Research Center, Mail Stop 245-3, Moffett Field, CA 94035, USA 4The University of Arizona, Tuscon AZ 85721, USA 5School of Earth & Space Exploration, Arizona State University, Tempe AZ 85287, USA 6Department of Astronomy, University of Texas at Austin, Austin, Texas 78712, USA (Received August 8, 2020; Revised April 29, 2021; Accepted May 5, 2021) Submitted to ApJ ABSTRACT We present a large uniform forward-modeling analysis for 55 late-T (T7−T9) dwarfs, using low-resolution (R ≈ 50−250) near- infrared (1:0 − 2:5 µm) spectra and cloudless Sonora-Bobcat model atmospheres. We derive the objects’ effective temperatures, surface gravities, metallicities, radii, masses, and bolometric luminosities using our newly developed Bayesian framework, and use the resulting population properties to test the model atmospheres. We find (1) our objects’ fitted metallicities are 0:3−0:4 dex lower than those of nearby stars; (2) their ages derived from spectroscopic parameters are implausibly young (10 Myr−0:4 Gyr); (3) their fitted effective temperatures show a similar spread as empirical temperature scales at a given spectral type but are ∼ 50 − 200 K hotter for >T8 dwarfs; and (4) their spectroscopically inferred masses are unphysically small (mostly 1 − 8 MJup). -

Commission 27 of the I.A.U. Information Bulletin on Variable Stars
COMMISSION 27 OF THE I.A.U. INFORMATION BULLETIN ON VARIABLE STARS Nos. 3301 - 3400 1989 March - 1989 December EDITORS: L. SZABADOS and B. SZEIDL KONKOLY OBSERVATORY H-1525 BUDAPEST P.O. Box 67, HUNGARY HU ISSN 0374 - 0676 CONTENTS 1989 No. Page 3301 M. ZEILIK, D. BECKERT, D. COX, J. DOLBY, M. LEDLOW, M. NEWBERRY and M. RHODES: 1989 V-Band Light Curve of RT And 1-3 3302 ZHANG JI-TONG, ZHANG RONG-XIAN, ZHAI DI-SHENG, LI QI-SHENG and JI-TIE-LIN: Photoelectric observations of AP Leonis and its Period Changes 1-3 3303 A.D. ANDREWS: A Relation Between X-Ray Surface Fluxes and U-Band "Time Signatures" in dMe Stars 1-3 3304 T. BANKS and E. BUDDING: Light Curves for XY UMa 1-4 3305 T. BANKS and E. BUDDING: Light Curves for CG Cygni 1-4 3306 BODIL E. HELT and KAARE S. JENSEN: Photometric Variability of the Spectroscopic Binary HD 133822 1-4 3307 V.N. POPOV and A.P. ANTOV: Rapid Variations of the X-Ray Source KR Aurigae in U Colour 1-2 3308 I.A. VASIL'EV, V.P. MEREZHIN, V.N. NALIMOV, V.A. NOVOSYOLOV: On the Variability of Vega 1-2 3309 R. MARGONI, U. MUNARI, R. STAGNI and A. MAMMANO: V398 Cyg: Period Determination for an Unusual EA System 1-3 3310 D.E. MKRTICHIAN and YU.S. ROMANOV: The Dependence of the Effective Temperature Upon the Radius Variation in the Pulsating Variable Star XZ Cyg 1-3 3311 W. SEGGEWISS and K.P. PANOV: Photometric Stability of the Oxygen-Rich Wolf-Rayet Star ST 3(=WR 142) 1-4 3312 GABRIELA OPRESCU, MARIAN DORU SURAN, NEDELIA POPESCU: V Light Curve and Elements of the Binary System AH Cephei 1-3 3313 DANIEL H. -

Varstrometry for Off-Nucleus and Dual Sub-Kpc AGN (VODKA): Hubble
Draft version August 5, 2021 Typeset using LATEX twocolumn style in AASTeX62 Varstrometry for Off-nucleus and Dual sub-Kpc AGN (VODKA): Hubble Space Telescope Discovers Double Quasars Yu-Ching Chen,1, 2, 3 Hsiang-Chih Hwang,4 Yue Shen,1, 2 Xin Liu,1, 2 Nadia L. Zakamska,4 Qian Yang,1 and Jennifer I. Li1 1Department of Astronomy, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA 2National Center for Supercomputing Applications, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA 3Center for AstroPhysical Surveys, National Center for Supercomputing Applications, Urbana, IL, 61801, USA 4Department of Physics and Astronomy, Johns Hopkins University ABSTRACT Dual supermassive black holes (SMBHs) at ∼ kpc scales are the progenitor population of SMBH mergers and play an important role in understanding the pairing and dynamical evolution of massive black holes in galaxy mergers. Because of the stringent resolution requirement and the apparent rareness of these small-separation pairs, there are scarce observational constraints on this population, with few confirmed dual SMBHs at < 10 kpc separations at z > 1. Here we present results from a pilot search for kpc-scale dual quasars selected with Gaia Data release 2 (DR2) astrometry and followed up with Hubble Space Telescope (HST) Wide Field Camera 3 dual-band (F475W and F814W) snapshot imaging. Our targets are quasars primarily selected with the varstrometry technique, i.e., light centroid jitter caused by asynchronous variability from both members in an unresolved quasar pair, supplemented by sub-arcsec pairs already resolved by Gaia DR2. We find an overall high fraction of HST-resolved pairs among the varstrometry-selected quasars (unresolved in Gaia DR2), ∼ 30−50%, increasing toward high redshift (∼ 60 − 80% at z > 1:5). -

On the Hipparcos Photometry of Chemically Peculiar B, A, and F Stars?
ASTRONOMY & ASTROPHYSICS OCTOBER I 1998,PAGE93 SUPPLEMENT SERIES Astron. Astrophys. Suppl. Ser. 132, 93–97 (1998) On the Hipparcos photometry of chemically peculiar B, A, and F stars? Saul J. Adelman Department of Physics, The Citadel, 171 Moultrie Street, Charleston SC 29409, U.S.A. e-mail: [email protected] Received February 23; accepted March 20, 1998 Abstract. The Hipparcos photometry of the Chemically standard error as given in the Hipparcos Catalogue and Peculiar main sequence B, A, and F stars is examined the “amplitude”, the difference between the 95 th and for variability. Some non-magnetic CP stars, Mercury- 5 th percentile magnitudes from its Photometry Annex. Manganese and metallic-line stars, which according to The Hipparcos Catalogue gives the scatter (one-half the canonical wisdom should not be variable, may be vari- difference between the 85 th and 15 th percentile magni- able and are identified for further study. Some potentially tudes). Although the scatter and amplitude should cor- important magnetic CP stars are noted. relate with one another and with the standard error, the amplitude might be more sensitive to potentially eclipsing Key words: stars: early type — stars: chemically peculiar systems. Tables 1, 2, and 3 give the Hipparcos photometry for the HgMn, Am, and magnetic CP stars, respectively. For each star, two identifiers are normally given, the HR or HD number and the Hipparcos Catalogue number, the mean Hipparcos magnitude, its standard error, its am- 1. Introduction plitude, and variability comments including the period if known except for the magnetic CP stars. Photometry from the Hipparcos Satellite (European Space Agency (ESA) 1997) can be used to study stellar variabil- The standard error, the amplitude, and the scatter ity. -

Spots, Plages, and Flares on Λ Andromedae and II Pegasi
Astronomy & Astrophysics manuscript no. LAnd˙IIPeg˙07˙Nov c ESO 2018 October 30, 2018 Spots, plages, and flares on λ Andromedae and II Pegasi⋆ A. Frasca1, K. Biazzo1, G. Ta¸s2, S. Evren2, and A. C. Lanzafame3 1 INAF - Catania Astrophysical Observatory, via S. Sofia 78, I–95123 Catania, Italy 2 Ege University Observatory, Bornova, Izmir,˙ Turkey 3 Department of Physics and Astronomy, Astrophysics Section, University of Catania, via S. Sofia 78, I–95123 Catania, Italy Received 21 May 2007 / Accepted 7 November 2007 ABSTRACT Aims. We present the results of a contemporaneous photometric and spectroscopic monitoring of two RS CVn binaries, namely λ And and II Peg. The aim of this work is to investigate the behavior of surface inhomogeneities in the atmospheres of the active components of these systems which have nearly the same temperature but different gravity. Methods. The light curves and the modulation of the surface temperature, as recovered from line-depth ratios (LDRs), are used to map the photospheric spots, while the Hα emission has been used as an indicator of chromospheric inhomogeneities. Results. The spot temperatures and sizes were derived from a spot model applied to the contemporaneous light and temperature curves. We find larger and cooler spots on II Peg (Tsp ≃ 3600 K) compared to λ And (Tsp ≃ 3900 K); this could be the result of both the different gravity and the higher activity level of the former. Moreover, we find a clear anti-correlation between the Hα emission and the photospheric diagnostics (temperature and light curves). We have also detected a modulation of the intensity of the He i D3 line with the star rotation, suggesting the presence of surface features also in the upper chromosphere of these stars. -

The Hubble Catalog of Variables (HCV)? A
A&A 630, A92 (2019) Astronomy https://doi.org/10.1051/0004-6361/201936026 & c ESO 2019 Astrophysics The Hubble Catalog of Variables (HCV)? A. Z. Bonanos1, M. Yang1, K. V. Sokolovsky1,2,3 , P. Gavras4,1, D. Hatzidimitriou1,5, I. Bellas-Velidis1, G. Kakaletris6, D. J. Lennon7,8, A. Nota9, R. L. White9, B. C. Whitmore9, K. A. Anastasiou5, M. Arévalo4, C. Arviset8, D. Baines10, T. Budavari11, V. Charmandaris12,13,1 , C. Chatzichristodoulou5, E. Dimas5, J. Durán4, I. Georgantopoulos1, A. Karampelas14,1, N. Laskaris15,6, S. Lianou1, A. Livanis5, S. Lubow9, G. Manouras5, M. I. Moretti16,1, E. Paraskeva1,5, E. Pouliasis1,5, A. Rest9,11, J. Salgado10, P. Sonnentrucker9, Z. T. Spetsieri1,5, P. Taylor9, and K. Tsinganos5,1 1 IAASARS, National Observatory of Athens, Penteli 15236, Greece e-mail: [email protected] 2 Department of Physics and Astronomy, Michigan State University, East, Lansing, MI 48824, USA 3 Sternberg Astronomical Institute, Moscow State University, Universitetskii pr. 13, 119992 Moscow, Russia 4 RHEA Group for ESA-ESAC, Villanueva de la Cañada, 28692 Madrid, Spain 5 Department of Physics, National and Kapodistrian University of Athens, Panepistimiopolis, Zografos 15784, Greece 6 Athena Research and Innovation Center, Marousi 15125, Greece 7 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain 8 ESA, European Space Astronomy Centre, Villanueva de la Canada, 28692 Madrid, Spain 9 Space Telescope Science Institute, Baltimore, MD 21218, USA 10 Quasar Science Resources for ESA-ESAC, Villanueva de la Cañada, 28692 Madrid, Spain 11 The Johns Hopkins University, Baltimore, MD 21218, USA 12 Institute of Astrophysics, FORTH, Heraklion 71110, Greece 13 Department of Physics, Univ. -

Vec{Uvby}$ Photometry of the CP Stars HR 149, HD 32966, HD 171782, and HR 7911
A&A 390, 1023–1026 (2002) Astronomy DOI: 10.1051/0004-6361:20020761 & c ESO 2002 Astrophysics uvby photometry of the CP stars HR 149, HD 32966, HD 171782, and HR 7911? Saul J. Adelman and S. A. Meadows Department of Physics, The Citadel, 171 Moultrie Street, Charleston, SC 29409, USA Received 10 January 2002 / Accepted 23 May 2002 Abstract. Differential Str¨omgren uvby observations from the Four College Automated Photoelectric Telescope (FCAPT) are presented for the CP stars HR 149 and HR 7911 and the mCP stars HD 32966 and HD 171782. The Mercury-Manganese star HR 149 is found to be constant while HR 7911 with a period of 5.9617 days probably has a component which is a magnetic CP star. Improved periods were derived for HD 32966 and HD 171782 of 3.0927 and 4.4674 days, respectively. The former is a rather large amplitude mCP star. Both have at least one light curve different in shape from the others observed. Key words. stars: chemically peculiar – stars: individual: HR 149 – stars: individual: HD 32966 – stars: individual: HD 171782 – stars: individual: HR 7911 1. Introduction For each group of variable, check, and comparison stars, the telescope measures the dark count and then observes in This paper presents single-channel differential Str¨omgren uvby each filter sky-ch-c-v-c-v-c-v-c-ch-sky where sky is a read- photometry from the Four College Automated Photoelectric ing of the sky, ch of the check star, c of the comparison star, Telescope (FCAPT) at Washington Camp, AZ. -

Principles of Quantum Universe”
Principles of Quantum Universe V.N. Pervushin, A.E. Pavlov Laboratory of Theoretical Physics Joint Institute for Nuclear Research, Dubna February 4, 2014 arXiv:1402.0354v1 [gr-qc] 3 Feb 2014 Contents 1 Introduction 15 1.1 Whatisthisbookabout?. 15 1.2 Program ........................... 20 1.3 Does the creation and evolution of the Universedependonanobserver? . 28 1.4 Contents........................... 56 2 Initial data and frames of reference 62 2.1 Unitsofmeasurement . 62 2.2 Nonrelativisticmechanicsofaparticle . 64 2.3 FoundationsofSpecialRelativity. 66 2.3.1 Actionofarelativisticparticle . 66 2.3.2 Dynamicsofarelativisticparticle . 68 2.3.3 Geometrodynamics of a relativistic particle . 72 2.3.4 Reduction of geometrodynamics to the Planck’s relativistic dynamics (1906) . 75 2.3.5 Quantum anomaly of geometric interval . 77 2.3.6 How does the invariant reduction differfromthechoiceofgauge? . 80 2 CONTENTS 3 2.4 Homogeneous approximation of GeneralRelativity . 82 2.4.1 Radiation-dominated cosmological model . 82 2.4.2 Arrow of conformal time as quantum anomaly . 86 2.5 Standardcosmologicalmodels . 87 2.6 Summary........................... 89 3 Principles of symmetry of physical theories 94 3.1 Irreducible representations of Lorentzgroup ........................ 94 3.2 Irreducible representations of Poincar´egroup. 97 3.3 Weylgroup..........................101 3.4 ConformalgroupC . .104 3.5 Conformal invariant theories ofgravitation ........................106 3.6 Affine group A(4) ......................117 3.7 Fundamental elements of base Minkowskian space M .................118 3.8 Summary...........................120 4 Nonlinearrealizationsofsymmetrygroups 123 4.1 DifferentialformsofCartan. 123 4.2 Structuralequations. .132 4.3 Exponentialparametrization . 135 4.4 Algebraic and dynamical principlesofsymmetry . .136 4 CONTENTS 4.5 Theory of gravitation as nonlinear realization of A(4) C ...................140 ⊗ 4.5.1 Derivation of action of General Relativity . -

Análisis Estadístico De Estrellas De Hgmn 1 MARCO TEÓRICO
AnAnáálisislisis EstadEstadíísticostico dede EstrellasEstrellas dede HgMnHgMn por Natalia Edith Nuñez Presentado ante la Facultad de Matemática, Astronomía y Física como parte de los requerimientos para la obtención del grado de Doctor en Astronomía de la UNIVERSIDAD NACIONAL DE CORDOBA Marzo, 2012 ©FaMAF ± UNC 2012 Director: Jorge Federico Gónzalez Codirector: Emilio Lapasset Gomar ÌNDICE GENERAL 1. MARCO TEÓRICO 1.1. Conceptos sobre clasificación ..................................................................... 1 1.2. Escala de temperaturas ¼...............................¼....................................... 4 1.3. Multiplicidad y rotación ¼.......................................................................... 5 1.4. Abundancias químicas ................................................................................ 6 1.5. Estratificación ............................................................................................. 7 1.6. Procesos físicos ............................................................................................ 8 1.7. Campos magnéticos y manchas químicas ¼.............................................. 10 2. RELEVAMIENTO 2.1. Introducción ¼............................................................................................. 12 2.2. Instrumental: espectrógrafo REOSC ......................................................... 14 2.3. Criterios de selección .................................................................................. 15 2.4. Adquisición y reducción ............................................................................. -

List of Mutual Funds
List of Mutual Funds Cayman Islands Monetary Authority P.O. Box 10052 80e Shedden Road, Elizabethan Square Grand Cayman, KY1-1001 CAYMAN ISLANDS Licence # Mutual Fund Name Registration Type Registration Date 15279 "RICI" Commodity Fund Ltd. Registered 12-Jun-2008 670810 1 North Equity Healthcare Long/Short Master Fund Ltd. Master Fund 01-Oct-2013 1337361 1060 Capital Opportunity Fund, Ltd. Registered 01-Jan-2017 583634 12 West Capital Fund Ltd Registered 30-Sep-2011 649736 12 West Capital Offshore Fund LP Master Fund 22-Feb-2013 1322580 1798 Credit Convexity Fund Ltd Registered 27-Sep-2016 1322591 1798 Credit Convexity Master Fund Ltd Master Fund 27-Sep-2016 1343904 1798 Event Convexity Fund Ltd Registered 31-Jan-2017 1343915 1798 Event Convexity Master Fund Ltd Master Fund 31-Jan-2017 1281151 1798 Fundamental Equities Fund Ltd Registered 01-Mar-2016 605356 1798 Fundamental Equities Master Fund Ltd Master Fund 14-Mar-2012 14237 1798 Fundamental Strategies Fund Ltd Registered 16-Nov-2007 1324433 1798 Global Macro Fund Ltd Registered 06-Oct-2016 1304741 1798 Global Macro Master Fund Ltd Master Fund 30-Jun-2016 6845 1798 UK Small Cap Best Ideas Fund Ltd Registered 08-Aug-2003 1278351 1798 Volantis Catalyst Fund II Ltd Registered 15-Feb-2016 633566 1798 Volantis Catalyst Fund Ltd Registered 23-Jul-2012 5584 1798 Volantis Fund Ltd Registered 02-May-2002 4325 1818 Master Partners, Ltd. Registered 23-Feb-2001 4326 1818 Partners (Offshore), L.P. Registered 23-Feb-2001 1298404 1824 Fund, Ltd. Registered 03-Jun-2016 12379 1837 PARTNERS, LTD. Registered 02-Jan-2007 671392 2013-10 US Corporate Bond Fund Registered 15-Oct-2013 1254643 2015 Schroder Asian IG Corporate Bond Fund Registered 31-Aug-2015 1231414 2015 Schroder Euro IG Corporate Bond Fund Registered 17-Jun-2015 1294064 2016 SCH Asia IG Corporate Bond Fund Registered 09-May-2016 1290531 2016 SCH Euro IG Corporate Bond Fund Registered 15-Apr-2016 11908 21 April Fund, Ltd. -
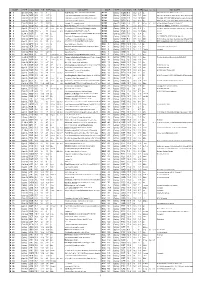
7000 List by Name
NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES NAME TYPE CON MAG S.B. SIZE Class ns bs SAC NOTES M 1 SN Rem TAU 8.4 11 8' Crab Nebula; filaments;pulsar 16m;3C144 -M 99 Galaxy COM 9.9 13.2 5.3' Sc SN 1967h;Norton-diff for small scope M 2 Glob CL AQR 6.5 11 11.7' II Lord Rosse-Dark area near core;* mags 13... -M 100 Galaxy COM 9.4 13.4 7.5' SBbc SN 1901-14-59;NGC 4322 @ 5.2';NGC 4328 @ 6.1' M 3 Glob CL CVN 6.3 11 18.6' VI Lord Rosse-sev dark marks within 5' of center -M 101 Galaxy UMA 7.9 14.9 28.5' SBc P w NGC 5474;SN 1909;spir galax w one heavy arm; M 4 Glob CL SCO 5.4 12 26.3' IX Look for central bar structure -M 102 Galaxy DRA 9.9 12.2 6.5' Sa vBN w dk lane and ansae;NGC 5867 small E neb; M 5 Glob CL SER 5.7 11 19.9' V st mags 11...;superb cluster -M 103 Opn CL CAS 7.4 11 6' III 2 p 40 10.6 in Cas OB8;incl Struve 131 6-9m 14'' M 6 Opn CL SCO 4.2 10 20' III 2 p 80 6.2 Butterfly cluster;51 members to 10.5 mag incl var*- BMM104 Sco Galaxy VIR 8 11.6 8.6' Sab Sombrero Galaxy; H I 43;dark equatorial lane; M 7 Opn CL SCO 3.3 12 80' II 2 r 80 5.6 80 members to 10th mag; Ptolemy's cluster -M 105 Galaxy LEO 9.3 12.8 5.3' E1 P w NGC 3384 @ 7.2';NGC 3389 @ 10 ';Leo Group M 8 Opn CL SGR 4.6 - 15' II 2 m n 6.9 In Lagoon nebula M8;25* mags 7..