University of Bath
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
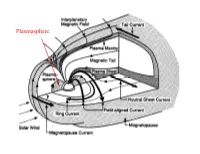
Plasmasphere Last Time We Started Talking About
Plasmasphere Last time we started talking about: Why does the plasmashere corotate? Review hot, cold drifts Discuss Alfven Shielding Layer Put it all together Then introduce Ionosphere subjects Plasma density 100 or 1000 times higher than outer magnetosphere Field Aligned Currents Region 1 (inner) Region 2 (outer) Ijima&Potemera Now, lets put it together • How do we explain Region 1 and Region 2 field aligned currents? • Region 1 is driven by magnetopause charge separation • Region 2 is driven by partial ring current • Next: what about aurora? Partial Ring Current: energetic particles Grad- B drift but don’t make it all the way around the earth Equatorial Plane View Plasmasphere corotates with Earth once a day Equatorial Plane View Plasmasphere corotates with Earth once a day Magnetic activity index Very High Density Moving from magnetosphere to ionosphere • Field aligned currents • Ionosphere structure • Ionosphere currents, What is σ? – 1. below 85 km altitude σ is isotropic – 2. 85 to 150 km (D and E regions) σ is tensor – 3. above 150 km σ is just σ|| • Then: put it all together Three views of ionosphere structure • Electron density • Thermal structure • Ion density and source Free electrons e- Negative ions Ionsopheric currents • J = σ E Ohms Law • We know there are large scale E fields (why), so what is σ in the ionosphere? What is Conductivity? • The scalar conductivity σ is defined as the ratio of the current density to the electric field strength σ = J/E. For a resistive medium this is just the Spitzer conductivity: • To get the components look at • So, σ can have many components: (Another way to derive scalar conductivity) Conductivity when particles gyrate σ becomes a matrix . -

THEMIS ESA First Science Results and Performance Issues
Space Sci Rev DOI 10.1007/s11214-008-9433-1 THEMIS ESA First Science Results and Performance Issues J.P. McFadden · C.W. Carlson · D. Larson · J. Bonnell · F. Mozer · V. Angelopoulos · K.-H. Glassmeier · U. Auster Received: 5 April 2008 / Accepted: 25 August 2008 © Springer Science+Business Media B.V. 2008 Abstract Early observations by the THEMIS ESA plasma instrument have revealed new details of the dayside magnetosphere. As an introduction to THEMIS plasma data, this pa- per presents observations of plasmaspheric plumes, ionospheric ion outflows, field line reso- nances, structure at the low latitude boundary layer, flux transfer events at the magnetopause, and wave and particle interactions at the bow shock. These observations demonstrate the ca- pabilities of the plasma sensors and the synergy of its measurements with the other THEMIS experiments. In addition, the paper includes discussions of various performance issues with the ESA instrument such as sources of sensor background, measurement limitations, and data formatting problems. These initial results demonstrate successful achievement of all measurement objectives for the plasma instrument. Keywords THEMIS · Magnetosphere · Magnetopause · Bow shock · Instrument performance PACS 94.80.+g · 06.20.Fb · 94.30.C- · 94.05.-a · 07.87.+v 1 Introduction The THEMIS mission provides the first multi-satellite measurements of the dayside mag- netosphere, magnetopause and bow shock utilizing a string of pearls orbit near the ecliptic plane (Angelopoulos 2008). During a 7 month coast phase, the instruments were commis- sioned and cross-calibrated while spacecraft separations were adjusted from a few hundred J.P. McFadden () · C.W. Carlson · D. -

Effects of the Radiation Belt on the Plasmasphere Distribution
Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 12-2020 Effects of the Radiation Belt on the Plasmasphere Distribution Stefan Thonnard Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Plasma and Beam Physics Commons Recommended Citation Thonnard, Stefan, "Effects of the Radiation Belt on the Plasmasphere Distribution" (2020). All Graduate Theses and Dissertations. 8007. https://digitalcommons.usu.edu/etd/8007 This Dissertation is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. EFFECTS OF THE RADIATION BELT ON THE PLASMASPHERE DISTRIBUTION by Stefan Thonnard A dissertation submitted in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in Physics Approved: ______________________ ______________________ Robert Schunk, Ph.D. Eric Held, Ph.D. Major Professor Committee Member ______________________ ______________________ Bela Fejer, Ph.D. Charles Swenson, Ph.D. Committee Member Committee Member ______________________ ______________________ Mike Taylor, Ph.D. D. Richard Cutler, Ph.D. Committee Member Interim Vice Provost of Graduate Studies UTAH STATE UNIVERSITY Logan, Utah 2020 ii Copyright © Stefan Thonnard 2020 All Rights Reserved iii ABSTRACT Effects of the Radiation Belt on the Plasmasphere Distribution by Stefan Thonnard, Doctor of Philosophy Utah State University, 2020 Major Professor: Dr. Robert Schunk Department: Physics This study examines the distribution of plasmasphere ions in the presence of warmer radiation belt particles. Recent satellite observations of the radiation belts indicate the existence of a population of warm ions with energy 100 keV to 1 MeV trapped along magnetic field lines. -

Geospace Magnetosphere-Ionosphere
GEospace Magnetosphere-Ionosphere-Neutral Interaction (GEMINI) A science mission framework targeting the core of the globally coupled magnetosphere-ionosphere providing continuous data optimized for global model validation D. Mitchell (JHU/APL), P. Brandt (JHU/APL), E. Donovan (U. Calgary), M-C Fok (GSFC), S. Fuselier (Lockheed), D. Gallagher (MSFC), J. Goldstein (SwRI), J. Kozyra (U. Mich), R. Meier (NRL), S. Mende (UCB), T. Moore (GSFC), P. Newell (JHU/APL), S. Ohtani (JHU/APL), G. Parks (UCB), L. Paxton (JHU/APL), T. Sotirelis (JHU/APL), J. Spann (MSFC), R. Wolf (Rice) Introduction The Solar System is comprised of a collection of coupled systems. In fact it is one large system-of-systems in which the Sun is the primary source of energy. Earth, as our home, is the planet we know most about. We have ventured extensively into Earth’s immediate surroundings, called Geospace, and have learned how Geospace is intrinsically interconnected over diverse scales of space and time. Over time an armada of spacecraft have revealed extraordinary global phenomena such as geomagnetic storms, with plasma energized in the magnetosphere distorting its magnetic and electric fields leading to strong modification of the radiation belts, and ionospheric storms, in which large regions of Earth’s ionosphere are redistributed over the globe. Plasma and fields in both the ionosphere and magnetosphere are coupled with each other and multiple processes (precipitation, Joule heating, particle acceleration, wave generation, mass outflow) are competing simultaneously on global and local scales to produce the global phenomena we observe. Such a system requires simultaneous global and continuous measurements of the critical regions of the magnetosphere and ionosphere. -

Modeling of Topside Ionosphere and Plasmasphere
Modeling of Topside Ionosphere and Plasmasphere Shigeto Watanabe ( [email protected] ) Hokkaido University: Hokkaido Daigaku https://orcid.org/0000-0002-3058-0689 Yoshizumi Miyoshi Nagoya University: Nagoya Daigaku Fuminori Tsuchiya Tohoku University: Tohoku Daigaku Atsusi Kumamoto Tohoku University: Tohoku Daigaku Yoshiya Kasahara Kanazawa University: Kanazawa Daigaku Ayako Matsuoka Kyoto University: Kyoto Daigaku Iku Shinohara JAXA Full paper Keywords: Topside Ionosphere, Plasmasphere, Modeling, Machine learning, Hinotori satellite, Akebono satellite, Arase satellite Posted Date: April 7th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-380095/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/18 Abstract We developed a new topside ionosphere and plasmasphere model using a machine learning technique using approximately ve million electron density datasets from the Japanese satellites, namely, Hinotori, Akebono, and Arase. The topside ionosphere and plasmasphere model (TIP-model) can estimate electron densities at altitudes ranging from 500 km to 30,000 km in terms of latitude, longitude, universal time, season, and solar and magnetic activities with time history. The model shows the time-dependent 3D structure of the plasmasphere in response to solar and magnetic activities. The constructed TIP-model reproduces plasmapause, plasma tail/erosion of the plasmasphere, and the plasma escape near the magnetic pole. The total electron content (TEC) in the plasmasphere was also obtained through the integration of electron density from 2,000 km to 30,000 km altitudes. The TEC of the plasmasphere is approximately 5 TECU near the magnetic equator, and it depends strongly on geomagnetic latitude, longitude, local time, and solar and magnetic activities. -

3 the Magnetosphere 3-1 Formation of the Magnetosphere and Magnetospheric Plasma Regime
3 The Magnetosphere 3-1 Formation of the Magnetosphere and Magnetospheric Plasma Regime OBARA Takahiro The Earth's magnetosphere is formed by the plasma flow from the Sun; i.e. solar wind. This solar wind particle can enter the magnetosphere through non-MHD processes and pro- duces specific regions of plasma. This is due to the convection motion seen in the magne- tosphere. An enhancement of the magnetospheric convection causes storms and sub- storms in the magnetosphere. Highly energetic particles can be produced through very effi- cient acceleration processes during the storms. In this paper we describe the fundamental physics of the magnetosphere, aiming a transition of researches to the Space Weather fore- cast. Keywords Magnetosphere, Plasma, Magnetospheric convection, Storms and substorms, Ener- getic particles 1 Outline of the Formation of the in the southern hemisphere. Magnetosphere and the Mag- There is an influx of solar wind plasma netospheric Plasma Structure particles in the lobe region. The area of the lobe near the magnetopause is referred to as The magnetosphere is a distinct region in the mantle. The magnetic field intensity is space surrounding the Earth, and its structure low near the equatorial plane, where the north- has been the subject of numerous detailed ern and southern lobes meet. Hot plasma satellite observations. Fig.1 shows a represen- accumulates in this region, referred to as the tation of this structure, with the upper front plasma sheet. Characteristic plasma regimes quarter removed to show the interior. The are present near the Earth, with plasma with Earth is at the center, and the solar wind flows higher energies relative to the plasma sheet. -

Empirical Modeling of the Plasmasphere Dynamics Using Neural Networks
Originally published as: Zhelavskaya, I. S., Shprits, Y., Spasojević, M. (2017): Empirical Modeling of the Plasmasphere Dynamics Using Neural Networks. - Journal of Geophysical Research, 122, 11, pp. 11,227—11,244. DOI: http://doi.org/10.1002/2017JA024406 Journal of Geophysical Research: Space Physics RESEARCH ARTICLE Empirical Modeling of the Plasmasphere 10.1002/2017JA024406 Dynamics Using Neural Networks Key Points: • We developed a dynamic Irina S. Zhelavskaya1,2 , Yuri Y. Shprits1,2,3 , and Maria Spasojevic´4 plasmasphere density model by applying neural networks to in 1Helmholtz Centre Potsdam, GFZ German Research Centre for Geosciences, Potsdam, Germany, 2Institute of Physics and situ density measurements and 3 verifying with global images Astronomy, University of Potsdam, Potsdam, Germany, Department of Earth, Planetary, and Space Sciences, University of 4 • The optimal model takes as input California, Los Angeles, CA, USA, Hansen Experimental Physics Laboratory, Stanford University, CA, USA the 96 h time history of geomagnetic indices and accurately captures plume formation and evolution Abstract We present the PINE (Plasma density in the Inner magnetosphere Neural network-based • Using both solar wind data and geomagnetic indices as inputs Empirical) model - a new empirical model for reconstructing the global dynamics of the cold plasma slightly overfits the training data, density distribution based only on solar wind data and geomagnetic indices. Utilizing the density database and gaps in solar wind data obtained using the NURD (Neural-network-based Upper hybrid Resonance Determination) algorithm for are problematic the period of 1 October 2012 to 1 July 2016, in conjunction with solar wind data and geomagnetic indices, we develop a neural network model that is capable of globally reconstructing the dynamics of the cold Correspondence to: plasma density distribution for 2 ≤ L ≤ 6 and all local times. -

On the Sources of Cold and Dense Plasma in Plasmasphere Drainage Plumes 3 Naomi Maruyama1,2, Michael H
Confidential manuscript submitted to Journal of Geophysical Research—Space Physics 1 2 On the Sources of Cold and Dense Plasma in Plasmasphere Drainage Plumes 3 Naomi Maruyama1,2, Michael H. Denton3,4, Yukitoshi Nishimura5, Michael G. Henderson6, 4 Philip G. Richards7, Mariangel Fedrizzi1,2, Anthea Coster8, Jacques Middlecof9,10, Timothy 5 J. Fuller-Rowell1,2, Mark Govet10, and Joachim Raeder11 6 1Cooperative Institute for Research in Environmental Sciences, University of Colorado, Boulder, 7 CO 80305, USA. 8 2Space Weather Prediction Center, National Oceanic and Atmospheric Administration, Boulder, 9 CO 80305, USA. 10 3Center for Space Plasma Physics, Space Science Institute, Boulder, CO 80301, USA. 11 4New Mexico Consortium, Los Alamos, NM 87544, USA. 12 5Boston University, Boston, MA, USA. 13 6ISR-1, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. 14 7Department of Physics and Astronomy, George Mason University, Fairfax, VA, USA. 15 8Haystack Observatory, MIT, MA, USA 16 9Cooperative Institute for Research in the Atmosphere, Colorado State University, Fort Collins, 17 CO, USA. 18 10Global Systems Division, National Oceanic and Atmospheric Administration, Boulder, CO 19 80305, USA. 20 11University of New Hampshire, Durham, NH, 03824, USA. 21 22 23 Corresponding author: first Naomi Maruyama ([email protected]) 24 Key Points: 25 • Plumes were simultaneously observed in the ionosphere, plasmasphere and near the 26 dayside magnetopause. 27 • Ionospheric SED plumes were magnetically conjugate features, but their magnitude and 28 structures were not. 29 • A larger storm does not necessarily have larger plume peak density in the ionosphere and 30 plasmasphere. 31 Confidential manuscript submitted to Journal of Geophysical Research—Space Physics 32 Abstract 33 Previous observations have revealed that the ionospheric Storm Enhanced Density (SED) plumes 34 are colocated with the cold, dense plumes observed at the dayside magnetopause. -

We Live Inside an Invisible Magnetosphere That Protects Life from Dangerous Solar Particle Radiation
We live inside an invisible magnetosphere that protects life from dangerous solar particle radiation UK experiments on the 4 spacecraft Cluster mission investigate the magnetosphere We are using Cluster to explore what makes the aurora borealis (the northern lights) We live inside an invisible magnetosphere that protects life from dangerous solar particle radiation magnetopause bow shock cusp moon magnetotail cusp solar wind A coronal mass ejection (CME). In this image, a disk The Earth’s magnetosphere. The magnetopause is the edge of the magnetosphere. In front of the magnetosphere is a bow held by an arm in front of the camera creates an artifi- shock, where the supersonic solar wind is deflected around the sides. The magnetotail forms on the side facing away from cial eclipse. The Sun is shown as a white circle. The CME the Sun. The cusps are regions near the magnetic poles where the magnetosphere is particularly ‘leaky’. The Moon is is traveling out from the Sun to the right. (Image credit: also shown for context, at a time when it is in the magnetotail. The magnetosphere contains a variety of different plasmas SoHO/LASCO consortium/ESA/NASA) such as the plasmasphere (blue, low energy), the plasma sheet (green), the ring current (yellow) and the radiation belts (orange and red, high energy). The Earth’s magnetic field extends into space and forms a protective bubble called the magnetosphere. Acting like a shield, it deflects the solar wind - a constant flow of material from the Sun - around the Earth. The magnetosphere is largely invisible, and so it must be measured locally by satellites that ‘touch’, ‘taste’ and ‘hear’ the magnetosphere. -

Properties of Whistler Mode Waves in Earth's Plasmasphere and Plumes
1 1 Properties of whistler mode waves in Earth’s 2 plasmasphere and plumes 3 Run Shi1, Wen Li1, Qianli Ma2,1, Alex Green1, Craig A. Kletzing3, William S. Kurth3, 4 George B. Hospodarsky3, Seth G. Claudepierre4, Harlan E. Spence5, and Geoff D. Reeves6 5 6 1Center for Space Physics, Boston University, Boston, Massachusetts, USA. 7 2Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, 8 Los Angeles, California, USA. 9 3Department of Physics and Astronomy, University of Iowa, Iowa City, Iowa, USA. 10 4Space Sciences Department, The Aerospace Corporation, El Segundo, California, USA. 11 5Institute for the Study of Earth, Oceans, and Space, University of New Hampshire, 12 Durham, New Hampshire, USA. 13 6Space Science and Applications Group, Los Alamos National Laboratory, Los Alamos, 14 New Mexico, USA. 15 16 17 Corresponding author: 18 Wen Li 19 Center for Space Physics, Boston University, Boston, Massachusetts, USA 20 [email protected] 2 21 Key points 22 1. Whistler mode waves are statistically analyzed both inside the plasmasphere and in the 23 plumes based on Van Allen Probes observations. 24 2. The occurrence rate and amplitudes of whistler mode waves inside the plasmasphere and 25 plumes show dependence on L, MLT and geomagnetic activity. 26 3. The majority of whistler mode waves in plumes are suggested to be locally amplified 27 due to energetic electron injection. 3 28 Abstract 29 Whistler mode wave properties inside the plasmasphere and plumes are systematically 30 investigated using five-year data from Van Allen Probes. The occurrence and intensity of 31 whistler mode waves in the plasmasphere and plumes exhibit dependences on magnetic 32 local time (MLT), L and AE. -

The Plasmasphere
The Plasmasphere D. L. Gallagher, NASA/MSFC [email protected] Outline • What does the plasmasphere look like? • Where does it fit into Earth’s space environment? • What is L-shell? • What’s important about the plasmasphere? • What physical processes are going on? • A climate model and new data for it. • The quest to understand the new data. Exosphere-Plasmasphere (ionized gas) http://www.windows2universe.org/glossary/plasmasphere.html Plasmaspheric Shape Follows B-Field Outline • What does the plasmasphere look like? • Where does it fit into Earth’s space environment? • What is L-shell? • What’s important about the plasmasphere? • What physical processes are going on? • A climate model and new data for it. • The quest to understand the new data. The Terrestrial Magnetosphere inside the Heliosphere Earth’s Atmosphere (Neutral Gas) http://www.slideshare.net/cherryloucanada/the-earths-atmosphere-atmospheric-layers?related=1 The Magnetosphere http://info.geomag.us/Magnetosphere/magnetosphere.jpg Outline • What does the plasmasphere look like? • Where does it fit into Earth’s space environment? • What is L-shell? • What’s important about the plasmasphere? • What physical processes are going on? • A climate model and new data for it. • The quest to understand the new data. McIlwain L-Shell Parameter https://en.wikipedia.org/wiki/L-shell#/media/File:L_shell_global_dipole.png http://www.met.reading.ac.uk/pplato2/h-flap/phys4_2.html Outline • What does the plasmasphere look like? • Where does it fit into Earth’s space environment? • What is L-shell? • What’s important about the plasmasphere? • What physical processes are going on? • A climate model and new data for it. -

Magnetosphere-Ionosphere Connector (MAGIC): Investigation of Magnetosphere-Ionosphere Coupling from High-To-Low Latitudes
MAGnetosphere-Ionosphere Connector (MAGIC): Investigation of Magnetosphere-Ionosphere Coupling from High-to-Low Latitudes A White Paper submitted to 2013 Solar and Space Physics Decadal Survey Shing F. Fung ([email protected]) Robert F. Benson Joseph M. Grebowsky George V. Khazanov NASA/Goddard Space Flight Center, Greenbelt, Maryland Donald L. Carpenter (Emeritus) STAR Laboratory, Stanford University, Stanford, California Abstract An outstanding challenge in Heliophysics is to understand the physics of systemic coupling between the magnetosphere and ionosphere from hemisphere to hemisphere, and the roles played by the intervening plasmasphere. Measurements from past missions like the dual Dynamics Explorers (DE), Polar, and IMAGE have shown the complexities of the inner magnetosphere. Yet, we still do not have a coherent understanding of the multi-scale processes and their interrelationships that couple the ionosphere and magnetosphere from high to low latitudes. DE, Polar and IMAGE clearly demonstrated the importance of global-scale imaging in providing the context for understanding local measurements. Except for DE limited to high latitudes, imaging observations from Polar and IMAGE were seldom accompanied by coordinated in situ observations of targeted regions. For example, plasmasphere imaging by IMAGE EUV were performed at L > 4 and near apogee (~ 8 Re), but in situ or radio-sounding measurements of the plasmasphere were best when the IMAGE Radio Plasma Imager was nearer the plasmasphere (L < 4). Plasmaspheric mass loss through large-scale plumes has been confirmed by IMAGE, although quantitative knowledge of such losses and their impact on the ionosphere and magnetosphere are still lacking. IMAGE also revealed numerous previously unknown plasmapause structures, such as notches, fingers, and shoulders, indicating much unknown about the coupling processes of ionosphere- plasmasphere-magnetosphere system.