The Steel Square and Its Uses, Introductory Remarks
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
Precision Shop Tools
Precision, Quality, Innovation PRECISION SHOP TOOLS Band Saw Blades Force Measurement Jobsite & Workshop Tools Laser Measurement Metrology Equipment Precision Granite Precision Ground Solutions Precision Measuring Tools PTA & Hand Tools Roundness Measurement Service Webber Gauge Blocks Catalogue 74E PRECISION, QUALITY, iNNOVATiON For more than 132 years, manufacturers, builders and craftsmen worldwide have depended upon precision tools and saws from The L.S. Starrett Company to ensure the consistent quality of their work. They know that the Starrett name on a saw blade, hand tool or measuring tool ensures exceptional quality, innovative products and expert technical assistance. With strict quality control, state-of-the-art equipment and an ongoing commitment to producing superior tools, the thousands of products in today’s Starrett line continue to be the most accurate, robust and durable tools available. This catalogue features those tools most widely used on a jobsite or in a workshop environment. 2 PUNCHES More than 10 models between automatic centre punches with adjustable stroke, centre punches with round shanks, with square shanks, for prick punches, square head nail sets, drive pin punches and brass drive pin punches. 5 Machinists’ levels Starrett offers a wide variety of levels, many for jobsite and workshop applications. This section has a different type of level – precisely made metal tools with ground surfaces designed specifically for machine shop and toolroom use. Products include our Master Precision Level, machinists’ levels with ground and graduated vials, precision bench levels with double plumbs available at up to 600mm / 24", cross test levels, bench levels and a nickel plated pocket level. 13 SHOP TOOLS A wide variety of gauges and precision hand tools designed for the delicate shop work of machinists and toolmakers. -

Essential Marking & Measuring
HARRISON & CLOUGH LTD ESSENTIAL MARKING & MEASURING LEADING BRANDS INNOVATION VALUE FOR MONEY All available from the experts - Harrison & Clough Ltd Harrison & Clough Ltd. Tel • 0844 571 22 22 P.O. Box 9, Keighley, Fax • 0844 571 22 33 West Yorkshire, Email • [email protected] BD21 4EG. Website • www.harclo.com BMI Levels BMI manufacture high-quality measurement tools for the most diverse of applications. The products meet the highest demands of trade and industry combining tradition and innovation. A further indication of the continuous innovation by BMI are the 40 active patents. Two of BMI patented milestones in the development and production of practical measuring instruments include: The introduction of unique spirit levels in 1986 whose vials have been fixed by means of ULTRASONIC WELDING, and the high-tech manufacture of the EUROSTAR range with unbreakable laser - marked vials since 1997. All BMI’s efforts follow the intention to equip merchants with up-to-date, marketable quality measuring instruments to lead the market. BMI Super Robust R1000 6605T691060S 600mm List Price: £68.99 6605T691080S 800mm List Price: £72.99 6605T691090S 1000mm Ultrasonic welded List Price: £79.99 Round vials for reflection vials free readability Extremely sturdy 4-chamber 2mm aluminimum profile 6605T691120S 1200mm box section List Price: £93.99 6605T691180S 1800mm List Price: £119.99 Thick rubber end caps Original Super Robust Vial bubbles move 5x faster than those of ordinary levels. Therefore inaccuracies can be recognised much sooner Harrison & Clough Ltd. Tel • 0844 571 22 22 P.O. Box 9, Keighley, Fax • 0844 571 22 33 1 West Yorkshire, Email • [email protected] BD21 4EG. -

18. Workshop Equipment
WORKSHOP EQUIPMENT Innovation is our mission! GD_KP_$KT-K14-$KP-BETRIEBSEINRICHTUNG_#SALL_#APR_#V1.indb 530 16.04.2014 09:12:21 1 2 PAGE 3 WORKBENCHES 534 4 WORKBENCHES 534 - 536 5 6 BACK WALL SYSTEMS 536 7 WALL CUPBOARDS 536 8 CLOAKROOM CUPBOARD 536 9 HINGED DOOR CABINET 536 - 537 10 11 BENCH VICES 537 12 HOOK ASSORTMENT 538 - 542 13 HOLE WALL 542 - 543 14 SERVICE TROLLEYS 543 - 544 15 16 PLATFORM TROLLEY 544 17 PLATFORM 544 18 SUPPORTS 545 19 20 TRANSPORT TROLLEY 545 - 546 21 PROTECTIVE KNEELING MATS 546 22 STOOLS 546 23 AXLE STANDS 547 24 25 LIFTING TOOLS 547 26 WORKSHOP EQUIPMENT 547 27 i GD_KP_$KT-K14-$KP-BETRIEBSEINRICHTUNG_#SALL_#APR_#V1.indb 531 16.04.2014 09:12:21 WORKSHOP EQUIPMENT Multi-bonded wooden plate, waterproof and resistant to chemicals Various additional options: With surrounding metal protective edge With shelf Central locking with cylinder lock Stable steel frame Ball bearing mounted drawer runner, 100% pull-out, 35 kg load with continuous grip bar Lockable door 2 steering wheels with roller rotation brake, 125 mm roller • Workbenches suitable for any requirement. • Diverse program for an intelligent system and good overview. • Many different combinations of drawers and doors. • Different lengths from 600 mm to 2,000 mm. Fixed workbenches or workbenches with fixable ollers.r • All workbenches are made of sturdy folded sheet steel. • Surfaces are treated with an environmentally friendly powder coating. • Individual workplace design with many different combination possibilities. GD_KP_$KT-K14-$KP-BETRIEBSEINRICHTUNG_#SALL_#APR_#V1.indb 532 16.04.2014 09:12:23 Perforated plates 10 standard colours, 4 different sizes = 40 variations Available in other colours as desired. -

SATURDAY MAY 6, 2017 LIST Humboldt Antique Tool Auction May
SATURDAY MAY 6, 2017 LIST Humboldt Antique Tool Auction May 5 and May 6, 2017 Humboldt Fairgrounds 311 6th Ave. North Humboldt, IA 50548 Preview Friday 2:00 to 3:35 PM Friday Auction begins 3:35 PM Preview Saturday 8:00 to 9:35 AM Saturday Auction begins 9:35 AM The lots marked TBA will be filled with items taken the three pallets of in-the-rough gear we cleaned out of a Wisconsin barn and then put in storage in Humboldt. Included in this lot will be buggy jacks, barn pulleys, a cast iron body of the cream separator and a wide variety of other antique tools and farm tools. We will lay this gear out in beer flats and individual lots and will number them in order Friday 180-184; 234-250; and 277-290 & on Saturday: 300, 441-449; and 597-625. 1 ______ Winchester 3026C wide body jack plane, tote broken in center and needing glue, will clean to very good overall. 2 ______ Stanley #92 shoulder plane with light rust on MADE IN USA blade, very good overall. 3 ______ Belknap BLUEGRASS iron jack plane, fine except for patch of rust on bottom where it sat on a damp shelf, will clean to fine overall. 4 ______ Scarce Stanley #94 shoulder plane, the biggest one they made, this one is complete and in very good overall condition, just needs a good cleaning. 5 ______ Keen Kutter KK190 iron rabbet plane with very good original blade, nice japanning, complete with depth stop, very good overall. -

Michael Lloyd, Ph.D
Academic Forum 25 2007-08 Mathematics of a Carpenter’s Square Michael Lloyd, Ph.D. Professor of Mathematics Abstract The mathematics behind extracting square roots, the octagon scale, polygon cuts, trisecting an angle and other techniques using a carpenter's square will be discussed. Introduction The carpenter’s square was invented centuries ago, and is also called a builder’s, flat, framing, rafter, and a steel square. It was patented in 1819 by Silas Hawes, a blacksmith from South Shaftsbury, Vermont. The standard square has a 24 x 2 inch blade with a 16 x 1.5 inch tongue. Using the tables and scales that appear on the blade and the tongue is a vanishing art because of computer software, c onstruction calculators , and the availability of inexpensive p refabricated trusses. 33 Academic Forum 25 2007-08 Although practically useful, the Essex, rafter, and brace tables are not especially mathematically interesting, so they will not be discussed in this paper. 34 Academic Forum 25 2007-08 Balanced Peg Hole Some squares have a small hole drilled into them so that the square may be hung on a nail. Where should the hole be drilled so the blade will be verti cal when the square is hung ? We will derive the optimum location of the hole, x, as measured from the corn er along the edge of the blade. 35 Academic Forum 2 5 2007-08 Assume that the hole removes negligible material. The center of the blade is 1” from the left, and the center of the tongue is (2+16)/2 = 9” from the left. -
METALS REFERENCE GUIDE the Following Pages Rep- Resent Sizes, Weights, and Dimensions of Carbon Steel, Stainless Steel and Alumi- Num Available from Stock
METALS REFERENCE GUIDE The following pages rep- resent sizes, weights, and dimensions of carbon steel, stainless steel and alumi- num available from stock. With one of the largest non-mill inventories in the U.S.A., stocked in six service centers, we have what your project requires. As an added service, all of our facilities maintain pro- cessing capabilities in-house. Whether you need material punched, flame cut, plasma cut, saw cut, sheared, shot blasted, painted, or bent, we can get the job done. On behalf of the Stein fam- ily and over 500 dedicated professionals, we thank you for your past patronage and hope to serve your needs again soon. Celebrating Over 50 Years of Service! Metal Reference Guide STEEL ALUMINUM ANGLES PlatES ANGLES . .26 . .48 Bar Angles . 4 Structural Angles....5-6 ROUND BARS CHANNELS BAR GRatinG . 19-20 . .49 . .44 SHEETS DIAMOND TREAD PlatES BEAMS . .52 Hot Rolled, Cold Rolled and Galvanized.... 27-28 PIPE Junior Beams . 8 Standard Beams . 7 SQUARE BARS . .54 Wide Flange Beams. 8-15 . .20 PlatES CHANNELS STRIP . .52 Bar Channel . 18 . .21 REctanGULAR MC Shapes BARS (Car, Ship and Jr.) 17-18 . .51 Stair Stringer . .18 Standard Channels....16 REctanGULAR TUBE TUBE CONCRETE REIN- Rectangular Tube..31-33 . .53 FORCING BARS Round Tube .........34 . .21 Square Tube . .29-31 ROUND BARS EXpandED MEtal UNIVERSAL MILL . 49-50 PlatES . .25 SHEETS Flattened . 43 Grating ............43 . .50 Standard...........42 STAINLESS NEW! SQUARE TUBE Flat BARS STEEL . .53 . 22-24 Stainless Angles . .44 Stainless Channels....45 FLOOR PlatES Decimal Equivalents ...58 Stainless Flats.......45 English and Metric . -

Downloaded 10/05/21 06:35 PM UTC Be Carefully Described, with Whatever Will Only Watch for Them
BULLETIN OF THE AMERICAN METEOROLOGICAL SOCIETY Entered as second class matter at the Post Office, Worcester, Massachusetts, under Act of Aug. 24, 1912. Issued monthly except July and August. Annual subscription, $2.00; single copies, 20c. Address all communications to Charles F. Brooks, Secretary Blue Hill Observatory, Harvard University Milton, Mass., U. S. A. Vol. 16 MARCH, 1935 No. 3 AN OPPORTUNITY FOR AMATEUR METEOROLOGISTS Rare and beautiful optical phe- what is desired. If there is more nomena of the atmosphere are some- than one ring, the diameters of all times missed at the major observa- the rings should be measured with tories, being of somewhat local special care. The nature of the cloud occurrence. Meteorologists not con- or fog producing the corona, and the nected with such institutions have in state of the weather should be noted consequence an opportunity of con- in full. Circular halos round the sun tributing to knowledge by describing or moon should also be measured as and measuring unusual halos, coronas, accurately as possible, since it seems rainbows, as well as twilight phe- likely that halos of unusual radii are nomena and the colors of the sky. sometimes missed because the ob- This note is written with the idea server has made the not unnatural that the American Meteorological So- assumption that it is the ordinary ciety1 might thus be able to assemble 22° or 46° halo which he sees. The a large amount of accurate informa- inner diameter of such halos should tion regarding such phenomena; not be given, and also the width of the mere descriptions, but angular meas- band and a description of the colors. -

Universal Protractor
Universal Protractor No. 52-448-612 No. 52-448-612 Fowler's Universal Protractor is a high precision angle gage with accurate worm gears. Eliminates intricate handling formerly needed with conventional vernier protractors. Recommended for use in gaging machines, metal patterns, layout work and installations. • Minimum reading: 1 minute. • Micrometer graduation: 1 minute per graduation (1 degree per revolution). • Includes 12" and 6" blades and a steel square for checking accuracy • Measures a full 360° angle range. • Round design for easy handling. Gage automatically locks when not in use. • Hardened stainless steel construction prevents rust which ensures long life. • Speedy set ups save time and money • Blades beveled 45 and 60°. • Built-in powerful magnifier make microfine graduations easy to read. • Accuracy: ± 2 minutes. Part Number Description 52-448-612 Universal Protractor. Universal Bevel Protractor Fowler's Universal Bevel Protractors feature a magnifying glass for easily reading verniers and dial. Levels & Protractors Levels • Finished in satin chrome for easy reading. • Accepts 6" and 12" blades. Blade slides full length, fastened by a knurled thumb lock which can be set at any point. Blades beveled 45° on one side; 60° on other. • Also available is an angle attachment for acute angle measuring. • Protractor dial graduated over 360° in 0 to 90° sectors and rotates around the full circle. Readings to 5 min. of arc with vernier. • Features a fine adjustment for exact settings. • Price includes fitted case. Part Number Description Grad. 52-440-612 Bevel protractor w/magnifier lens, 6" & 12" blade. 5 min. Accessories 52-445-005 6" blade for No. -

The Best Short Tape to Suit Your Needs
Including the most outstanding FatMax XL tapes and the world’s toughest levels Short Tapes 7 Long Tapes 19 Measuring Wheels 26 Rules 28 Levels 33 Marking Out Tools 45 Layout Tools 52 Chalk Lines 54 Padlock & Locksets 62 Others 64 HOW TO THE BEST SHORTTAPE CHOOSE TO SUITYOUR NEEDS Greater standout makesthem easier to use The curved steel blade,firstpioneered by Stanley, allows the tape to be extended unsupported, invaluableinsituations whereyou need to measure single handed across space suchas setting out roof trusses or measuringacrossdeep site excavations. Stanley’s FatMax XL hasanincredible market leading ‘stand out’ of 4metres. Themostreliable power return andblade locking system All Stanley’s short tapesfeature unbeatable power return andblade locking;key developments, whichStanley were the firsttopioneer with theirfamous ‘Powerlock’tape. Bladeprotection for durability Fordemanding environments choose atapewithaMylar® coatedblade, which provides up to 10 timesmore Stanley’s FatMax XL has an incredible market abrasion resistance than lacquered leading‘standout’ blades. Stanley’stop models of almost 4metres also have the additional protection of BladeArmor - TruZero end hook for athermoplastic coating greater accuracy over thefirst 15cms at Thestrongly riveted end hook is cleverly securedto the end of theblade, allow movement,which compensates forits own which is subject thickness, to provide the greatest accuracywhen to the harshest making internal or external measurements. treatment. The end hook on some models also features apencil -

S-T Industries Catalog.Pdf
354232_ST_Cover_z 4/12/07 10:19 AM Page 1 Form 40-0195-00 354232_ST_Cover_z 4/12/07 10:19 AM Page 2 FOUR REASONS FOR MAKING S-T YOUR SUPPLIER OF PRECISION MEASURING INSTRUMENTS KNOW-HOW Scherr-Tumico measuring tools have been a vital part of American industry for QWWWWWWWWWWWWWWWWWWWE 1 more than 65 years. During this period, we have developed the knowledge and RWWWWWWWWWWWWWWWWWWWT skills which provide our customers the ability to resolve most measuring problems. If you have a problem which cannot be handled by our standard tools, call us and RWWWWWWWWWWWWWWWWWWWT the chances are we will be able to provide you with the tools needed to get your WARRANTY job done. During the past 65 years, we have produced many millions of dollars in RWWWWWWWWWWWWWWWWWWWWithin one year from the date of purchase, any repairs necessary T special tools for American industries, both large and small. Put this experience to RWWWWWWWWWWWWWWWWWWWdue to defects in material or workmanship will be made without T work for you. charge by S-T INDUSTRIES, INC. This warranty does not apply to RWWWWWWWWWWWWWWWWWWWtools that have been modified, mishandled or misused, etched, T stamped or otherwise marked or damaged. This warranty applies to RWWWWWWWWWWWWWWWWWWWthe original purchaser and is not transferable. No other warranty, T QUALITY RWWWWWWWWWWWWWWWWWWWeither expressed or implied, shall be applicable. S-T INDUSTRIES, T All S-T products are subject to a rigorous 100% inspection process before they are INC.’s liability does not extend beyond the repair or replacement. 2 shipped to you. This process has been the major factor in making Scherr-Tumico RWWWWWWWWWWWWWWWWWWWT products welcome throughout the metalworking industry. -

The Multitalented Combination Square a Whole Lot of Tool in One Small Package by Andy Rae
The Multitalented Combination Square A whole lot of tool in one small package By Andy Rae Far more than just a tool to a combo square to true up that, I’ll discuss the two arenas in for checking “square,” the workpieces, lay out joints, and which the tool excels: measuring combination square is a do-all set up shop machines–all with a and laying out. Measuring shop tool. With its sliding ruler degree of precision that elevates includes performing machine locked to the head, you can use its status over other tools. setups, such as squaring bits it as a depth gauge, a marking To ensure this level of accuracy, and blades to tables and fences, gauge, a miter square, and a try as well as checking joints and square. Loosening the lock in the acquire a square that’s worthy of assemblies for accuracy. Laying head releases the rule for use yourthe first work. order Not of all business combination is to out involves making marks on as a straightedge or ruler. In a squares share the same quality your work, from drawing parallel pinch, you can employ the head and ease of use. In this article, lines and angles to marking as a small level, and a sharp awl we’ll take a look at the parts and centerlines and pinpointing tucked inside is always at the nomenclature of combination hardware locations. Read on to ready for marking. Thanks to squares, and I’ll describe what to these attributes, you can turn look for in a good tool. -
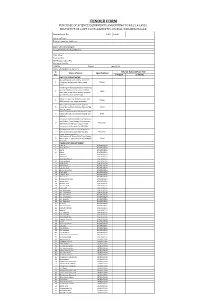
Tender Form Purchase of Science Equipments Amounting to Rs.21,41,453/- in Respect of Govt
TENDER FORM PURCHASE OF SCIENCE EQUIPMENTS AMOUNTING TO RS.21,41,453/- IN RESPECT OF GOVT. POSTGRADUATE COLLEGE, BAHAWALNAGAR. Tender Form No. /P&D Dated: Name of Firm: Firm's Complete Address: Name of Firm's Owner: Complete Residential Address: C.N.I.C No. Contact Nos. GST Registration No. National Tax No. CDR No. Dated: worth Rs. Name of Bank (CDR Issuer): Sr. Offered Rates without GST Name of Items Specifications No. In Figure In Words PHYSICS DEPARTMENT: Maxwell Needle with Hollow and Solid 1 Cylindrical Weights with Heavy Large Taiwan. stand. Travelling microscope precision heavy type vertical 180mm and horizontal 220mm 2 Japan scale with vernier three motion operated by rack and pinion special large. Diffraction grationg 15000 lines per inch 3 Taiwan. (600 lines per mm) Hilger and watts. Rheostate Sliding Resistance Large on 4 Heavy 280 x 60 mm Porcelain Pipe 0-1750 China ohms 0.3 Amp. Power Supply variable 0-30 volt DC 3 amp. 5 Fitted with volt and Ammeter Model WYJ- China. 3003 A. Ionization Potential of Mercury Apparatus with Bulit in Power Supply Micrommeter, 6 Pak Land. Voltmeter and Mercury Vapour Diode Complete in all Respects for 220 Volts. E/M Apparatus with vertical magnetron 7 tube double shade type tube coil & HT Pak Land. Power Supply complete. Oscillloscope 6” Screen Dual Trace Double 8 Beam 20MHZ. Sensitivity 1m V/Div Model China MOS-620. CHEMISTRY DEPARTMENT: 1 E.D.T.A E.MERCK BDH 2 Silver Nitrate E.MERCK BDH 3 Iodine E.MERCK BDH 4 Ether E.MERCK BDH 5 Ethanol E.MERCK BDH 6 Methanol E.MERCK BDH 7 Phenolphthalein E.MERCK BDH 8 Sodium Metal E.MERCK BDH 9 Anthracite E.MERCK BDH 10 X-Nephthol E.MERCK BDH 11 Salicylic Acid E.MERCK BDH 12 Acetic Anhydride E.MERCK BDH 13 Picric Acid E.MERCK BDH 14 Sulphur Acid E.MERCK BDH 15 Nitric Acid E.MERCK BDH 16 Hydrochloric Acid E.MERCK BDH 17 Acetic Acid E.MERCK BDH 18 Benzoic Acid E.MERCK BDH 19 Tartaric Acid E.MERCK BDH 20 Citric Acid E.MERCK BDH 21 Am.