DOCSLIB.ORG

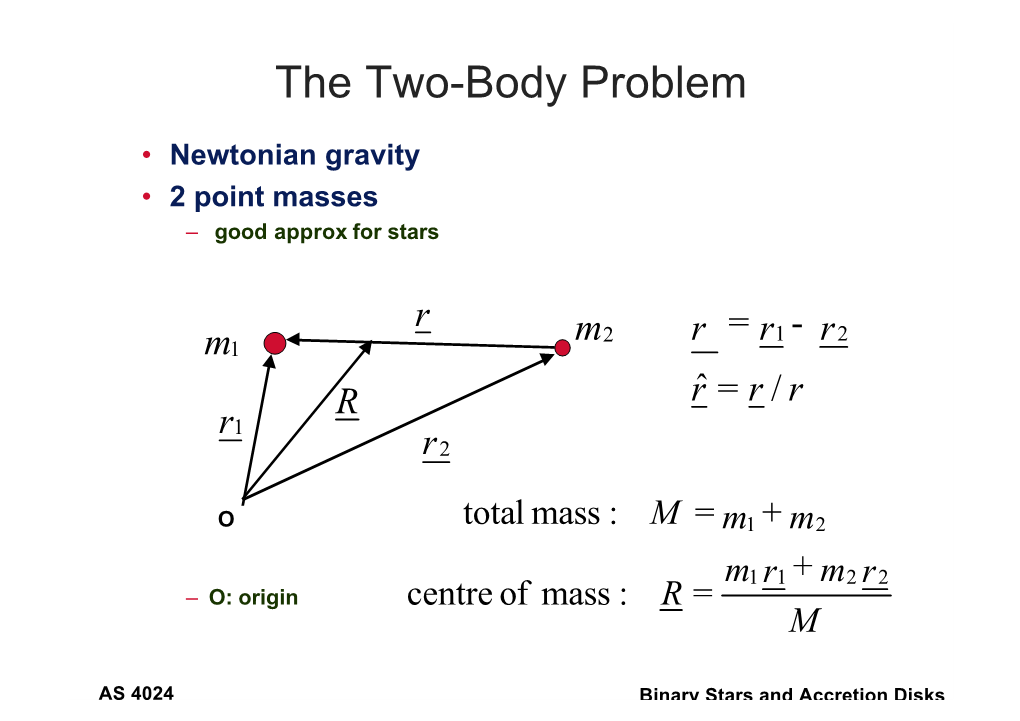
The Two-Body Problem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Two-Body Problem The Two-Body Problem • Newtonian gravity • 2 point masses – good approx for stars r m2 r = r1 - r2 m1 R rˆ = r / r r1 r2 O total mass : M = m1 + m2 m1 r1 + m2 r 2 – O: origin centre of mass : R = M AS 4024 Binary Stars and Accretion Disks Two-Body motion • Newtons laws of motion + law of gravitation Equations of motion : - Gm m F = m r&& = 1 2 rˆ F = m r&& = -F 1 1 1 r 2 2 2 2 1 add the equations m1 r&&1 + m2 r&&2 = 0 integrate dt m1 r&1 + m2 r&2 = A again m1 r1 + m2 r 2 = A t + B definition of R M R = A t + B •\ Centre of mass moves with constant velocity – ( unless acted on by an external force ) AS 4024 Binary Stars and Accretion Disks Relative Motion • Important for eclipses • Subtract two equations of motion -G M r&& = &r& -r&& = rˆ 1 2 r 2 • Multiply by m = m1 m2 / M = “reduced mass” - G M m - G m m m &r& = rˆ = 1 2 rˆ r 2 r 2 • Relative orbit is as if: – orbiter has reduced mass m = reduced mass – stationary central mass is M = total mass. AS 4024 Binary Stars and Accretion Disks The Relative Orbit m = m1 m2 M r&(t) r(t) M = m1 + m2 Important for Eclipses AS 4024 Binary Stars and Accretion Disks 2 EllipticalBarycentric Orbits Orbits R2 (t) R1(t) Important for Radial Velocities AS 4024 Binary Stars and Accretion Disks Barycentric Orbits • Important for radial velocity curves m1 R1 + m2 R2 = 0 centre of mass frame m1 + m2 M M r = R1 - R2 = R1 = R1 = - R2 m2 m2 m1 equations of motion : G m G m R&& = - 2 r R&& = - 1 (- r) 1 r 3 2 r 3 3 – Eliminate r using r = f(R1) and r = f(R1) : 3 R 3 R && G m2 1 && G m1 2 R1 = - 2 3 R2 = - 2 3 M R1 M R2 – the acceleration of each star relative to the centre of mass AS 4024 Binary Stars and Accretion Disks Relative vs Barycentric orbits – ( a, e, P, v ) relative orbit – ( a ,e, P ,v )1,2 barycentric orbits – m1 and m2 on straight line thru C P1 = P2 = P e1 = e2 = e a1 = a m2 / M a2 = a m1 / M a = a1 + a2 M = m1 + m2 a1 : a2 : a = V 1 :V 2 :V = m2 : m1 : M Kepler : p 2 M 3 / 2 3 / 2 4 = = m2 M = m1 M 2 3 3 3 GP a a1 a2 AS 4024 Binary Stars and Accretion Disks Orbital Speed orbital speed : V 2 = r& 2 + r 2q& 2 l conic section : r = 1 + e cos q d é l ù l 1 + e cos q = Þ -e ( sin q ) q& = - r& dt ëê r ûú r 2 specific angular momentum : r 2q& = L r 2q& L \ r& = e sin q = e sin q l l L L r q& = = (1 + e cos q ) r l AS 4024 Binary Stars and Accretion Disks Orbital Speed 2 æ L ö 2 V 2 = ç ÷ [e2 sin 2q + (1+e cos q ) ] è l ø L 2 2 l = æ L ö G M = ç ÷ [e2 + 1+ 2e cos J ] L G M è l ø = 2 l L æ L ö 2 = ç ÷ [2(ecos q +1)+e - 1 ] è l ø 2 2 2 L é 2 1- e ù V = ê - ú l ë r l û AS 4024 Binary Stars and Accretion Disks Orbital Speed 2 2 2 L é 2 1 - e ù V = ê - ú l ë r l û ellipse : l = a(1 - e 2) L 2 = GM l é 2 1 ù V 2 = GM - ëê r a ûú 2 2 é 2 1 ù ellipse e < 1 l = a(1 - e ) V = GM ê - ú ë r a û GM circle e = 0 l = a V 2 = a 2GM parabola e = 1 V 2 = r é 2 1 ù hyperbola e > 1 l = a(1 - e 2) V 2 = GM + ëê r a ûú AS 4024 Binary Stars and Accretion Disks Energy of Orbit Kinetic energy : 1 1 m m KE = T = m V 2 + m V 2 = 1 2 V 2 2 1 1 2 2 2 2 M æ 2 1 ö orbital speed : V 2 = G M ç - ÷ è r a ø Potential energy: ¥ G m1 m2 G m1 m2 PE = W = -ò 2 dr = - r r r G m m Total energy : E = T +W = - 1 2 < 0 2 a Binding energy : - E > 0 AS 4024 Binary Stars and Accretion Disks Angular momentum of the orbit • Angular momentum vector J, defines orbital plane 2 2 – J = m1L1 + m2L2 and L = G M a (1-e ) 2 3 2 ) 2 and L1 = G (m2 /M a1 (1-e ) and a1/a = m2 /M – same for L2 – hence m 2 m 2 L = 2 L; L = 1 L 1 M 2 2 M 2 therefore G m 2 m 2 J 2 = 1 2 a (1- e 2 ) M and the final expression for J is 2p a 2 m m J = 1 2 1- e 2 P M AS 4024 Binary Stars and Accretion Disks Orbital Angular momentum • Given masses m1,m2 and Energy E, – the angular momentum J determines the shape of the orbit – ie the eccentricity (or the conic section parameter l ) • For given E, – circular orbits have maximum J – J decreases as e -> 1 – orbit becomes rectilinear ellipse • relation between E, and J very important in determining when systems interact mass exchange and orbital evolution AS 4024 Binary Stars and Accretion Disks.
Load more

Recommended publications
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • Uncommon Sense in Orbit Mechanics
    AAS 93-290 Uncommon Sense in Orbit Mechanics by Chauncey Uphoff Consultant - Ball Space Systems Division Boulder, Colorado Abstract: This paper is a presentation of several interesting, and sometimes valuable non- sequiturs derived from many aspects of orbital dynamics. The unifying feature of these vignettes is that they all demonstrate phenomena that are the opposite of what our "common sense" tells us. Each phenomenon is related to some application or problem solution close to or directly within the author's experience. In some of these applications, the common part of our sense comes from the fact that we grew up on t h e surface of a planet, deep in its gravity well. In other examples, our mathematical intuition is wrong because our mathematical model is incomplete or because we are accustomed to certain kinds of solutions like the ones we were taught in school. The theme of the paper is that many apparently unsolvable problems might be resolved by the process of guessing the answer and trying to work backwards to the problem. The ability to guess the right answer in the first place is a part of modern magic. A new method of ballistic transfer from Earth to inner solar system targets is presented as an example of the combination of two concepts that seem to work in reverse. Introduction Perhaps the simplest example of uncommon sense in orbit mechanics is the increase of speed of a satellite as it "decays" under the influence of drag caused by collisions with the molecules of the upper atmosphere. In everyday life, when we slow something down, we expect it to slow down, not to speed up.
    [Show full text]
  • Orbital Mechanics
    Orbital Mechanics These notes provide an alternative and elegant derivation of Kepler's three laws for the motion of two bodies resulting from their gravitational force on each other. Orbit Equation and Kepler I Consider the equation of motion of one of the particles (say, the one with mass m) with respect to the other (with mass M), i.e. the relative motion of m with respect to M: r r = −µ ; (1) r3 with µ given by µ = G(M + m): (2) Let h be the specific angular momentum (i.e. the angular momentum per unit mass) of m, h = r × r:_ (3) The × sign indicates the cross product. Taking the derivative of h with respect to time, t, we can write d (r × r_) = r_ × r_ + r × ¨r dt = 0 + 0 = 0 (4) The first term of the right hand side is zero for obvious reasons; the second term is zero because of Eqn. 1: the vectors r and ¨r are antiparallel. We conclude that h is a constant vector, and its magnitude, h, is constant as well. The vector h is perpendicular to both r and the velocity r_, hence to the plane defined by these two vectors. This plane is the orbital plane. Let us now carry out the cross product of ¨r, given by Eqn. 1, and h, and make use of the vector algebra identity A × (B × C) = (A · C)B − (A · B)C (5) to write µ ¨r × h = − (r · r_)r − r2r_ : (6) r3 { 2 { The r · r_ in this equation can be replaced by rr_ since r · r = r2; and after taking the time derivative of both sides, d d (r · r) = (r2); dt dt 2r · r_ = 2rr;_ r · r_ = rr:_ (7) Substituting Eqn.
    [Show full text]
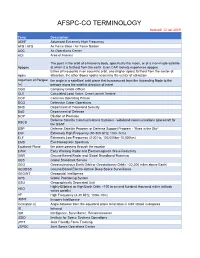
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • The Speed of a Geosynchronous Satellite Is ___
    Physics 106 Lecture 9 Newton’s Law of Gravitation SJ 7th Ed.: Chap 13.1 to 2, 13.4 to 5 • Historical overview • N’Newton’s inverse-square law of graviiitation Force Gravitational acceleration “g” • Superposition • Gravitation near the Earth’s surface • Gravitation inside the Earth (concentric shells) • Gravitational potential energy Related to the force by integration A conservative force means it is path independent Escape velocity Example A geosynchronous satellite circles the earth once every 24 hours. If the mass of the earth is 5.98x10^24 kg; and the radius of the earth is 6.37x10^6 m., how far above the surface of the earth does a geosynchronous satellite orbit the earth? G=6.67x10-11 Nm2/kg2 The speed of a geosynchronous satellite is ______. 1 Goal Gravitational potential energy for universal gravitational force Gravitational Potential Energy WUgravity= −Δ gravity Near surface of Earth: Gravitational force of magnitude of mg, pointing down (constant force) Æ U = mgh Generally, gravit. potential energy for a system of m1 & m2 G Gmm12 mm F = Attractive force Ur()=− G12 12 r 2 g 12 12 r12 Zero potential energy is chosen for infinite distance between m1 and m2. Urg ()012 = ∞= Æ Gravitational potential energy is always negative. 2 mm12 Urg ()12 =− G r12 r r Ug=0 1 U(r1) Gmm U =− 12 g r Mechanical energy 11 mM EKUrmvMVG=+ ( ) =22 + − mech 22 r m V r v M E_mech is conserved, if gravity is the only force that is doing work. 1 2 MV is almost unchanged. If M >>> m, 2 1 2 mM ÆWe can define EKUrmvG=+ ( ) = − mech 2 r 3 Example: A stone is thrown vertically up at certain speed from the surface of the Moon by Superman.
    [Show full text]
  • Lesson 3: Moons, Rings Relationships
    GETTING TO KNOW SATURN LESSON Moons, Rings, and Relationships 3 3–4 hrs Students design their own experiments to explore the fundamental force of gravity, and then extend their thinking to how gravity acts to keep objects like moons and ring particles in orbit. Students use the contexts of the Solar System and the Saturn system MEETS NATIONAL to explore the nature of orbits. The lesson SCIENCE EDUCATION enables students to correct common mis- STANDARDS: conceptions about gravity and orbits and to Science as Inquiry • Abilities learn how orbital speed decreases as the dis- Prometheus and Pandora, two of Saturn’s moons, “shepherd” necessary to Saturn’s F ring. scientific inquiry tance from the object being orbited increases. Physical Science • Motions and PREREQUISITE SKILLS BACKGROUND INFORMATION forces Working in groups Background for Lesson Discussion, page 66 Earth and Space Science Reading a chart of data Questions, page 71 • Earth in the Plotting points on a graph Answers in Appendix 1, page 225 Solar System 1–21: Saturn 22–34: Rings 35–50: Moons EQUIPMENT, MATERIALS, AND TOOLS For the teacher Materials to reproduce Photocopier (for transparencies & copies) Figures 1–10 are provided at the end of Overhead projector this lesson. Chalkboard, whiteboard, or large easel FIGURE TRANSPARENCY COPIES with paper; chalk or markers 11 21 For each group of 3 to 4 students 31 Large plastic or rubber ball 4 1 per student Paper, markers, pencils 5 1 1 per student 6 1 for teacher 7 1 (optional) 1 for teacher 8 1 per student 9 1 (optional) 1 per student 10 1 (optional) 1 for teacher 65 Saturn Educator Guide • Cassini Program website — http://www.jpl.nasa.gov/cassini/educatorguide • EG-1999-12-008-JPL Background for Lesson Discussion LESSON 3 Science as inquiry The nature of Saturn’s rings and how (See Procedures & Activities, Part I, Steps 1-6) they move (See Procedures & Activities, Part IIa, Step 3) Part I of the lesson offers students a good oppor- tunity to experience science as inquiry.
    [Show full text]
  • Calculation of Moon Phases and 24 Solar Terms
    Calculation of Moon Phases and 24 Solar Terms Yuk Tung Liu (廖²棟) First draft: 2018-10-24, Last major revision: 2021-06-12 Chinese Versions: ³³³qqq---文文文 简简简SSS---文文文 This document explains the method used to compute the times of the moon phases and 24 solar terms. These times are important in the calculation of the Chinese calendar. See this page for an introduction to the 24 solar terms, and this page for an introduction to the Chinese calendar calculation. Computation of accurate times of moon phases and 24 solar terms is complicated, but today all the necessary resources are freely available. Anyone familiar with numerical computation and computer programming can follow the procedure outlined in this document to do the computation. Before stating the procedure, it is useful to have a basic understanding of the basic concepts behind the computation. I assume that readers are already familiar with the important astronomy concepts mentioned on this page. In Section 1, I briefly introduce the barycentric dynamical time (TDB) used in modern ephemerides, and its connection to terrestrial time (TT) and international atomic time (TAI). Readers who are not familiar with general relativity do not have to pay much attention to the formulas there. Section 2 introduces the various coordinate systems used in modern astronomy. Section 3 lists the formulas for computing the IAU 2006/2000A precession and nutation matrices. One important component in the computation of accurate times of moon phases and 24 solar terms is an accurate ephemeris of the Sun and Moon. I use the ephemerides developed by the Jet Propulsion Laboratory (JPL) for the computation.
    [Show full text]
  • Up, Up, and Away by James J
    www.astrosociety.org/uitc No. 34 - Spring 1996 © 1996, Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, CA 94112. Up, Up, and Away by James J. Secosky, Bloomfield Central School and George Musser, Astronomical Society of the Pacific Want to take a tour of space? Then just flip around the channels on cable TV. Weather Channel forecasts, CNN newscasts, ESPN sportscasts: They all depend on satellites in Earth orbit. Or call your friends on Mauritius, Madagascar, or Maui: A satellite will relay your voice. Worried about the ozone hole over Antarctica or mass graves in Bosnia? Orbital outposts are keeping watch. The challenge these days is finding something that doesn't involve satellites in one way or other. And satellites are just one perk of the Space Age. Farther afield, robotic space probes have examined all the planets except Pluto, leading to a revolution in the Earth sciences -- from studies of plate tectonics to models of global warming -- now that scientists can compare our world to its planetary siblings. Over 300 people from 26 countries have gone into space, including the 24 astronauts who went on or near the Moon. Who knows how many will go in the next hundred years? In short, space travel has become a part of our lives. But what goes on behind the scenes? It turns out that satellites and spaceships depend on some of the most basic concepts of physics. So space travel isn't just fun to think about; it is a firm grounding in many of the principles that govern our world and our universe.
    [Show full text]
  • Particle Nature of Matter
    Solved Problems on the Particle Nature of Matter Charles Asman, Adam Monahan and Malcolm McMillan Department of Physics and Astronomy University of British Columbia, Vancouver, British Columbia, Canada Fall 1999; revised 2011 by Malcolm McMillan Given here are solutions to 5 problems on the particle nature of matter. The solutions were used as a learning-tool for students in the introductory undergraduate course Physics 200 Relativity and Quanta given by Malcolm McMillan at UBC during the 1998 and 1999 Winter Sessions. The solutions were prepared in collaboration with Charles Asman and Adam Monaham who were graduate students in the Department of Physics at the time. The problems are from Chapter 3 The Particle Nature of Matter of the course text Modern Physics by Raymond A. Serway, Clement J. Moses and Curt A. Moyer, Saunders College Publishing, 2nd ed., (1997). Coulomb's Constant and the Elementary Charge When solving numerical problems on the particle nature of matter it is useful to note that the product of Coulomb's constant k = 8:9876 × 109 m2= C2 (1) and the square of the elementary charge e = 1:6022 × 10−19 C (2) is ke2 = 1:4400 eV nm = 1:4400 keV pm = 1:4400 MeV fm (3) where eV = 1:6022 × 10−19 J (4) Breakdown of the Rutherford Scattering Formula: Radius of a Nucleus Problem 3.9, page 39 It is observed that α particles with kinetic energies of 13.9 MeV or higher, incident on copper foils, do not obey Rutherford's (sin φ/2)−4 scattering formula. • Use this observation to estimate the radius of the nucleus of a copper atom.
    [Show full text]
  • GRAVITATION UNIT H.W. ANS KEY Question 1
    GRAVITATION UNIT H.W. ANS KEY Question 1. Question 2. Question 3. Question 4. Two stars, each of mass M, form a binary system. The stars orbit about a point a distance R from the center of each star, as shown in the diagram above. The stars themselves each have radius r. Question 55.. What is the force each star exerts on the other? Answer D—In Newton's law of gravitation, the distance used is the distance between the centers of the planets; here that distance is 2R. But the denominator is squared, so (2R)2 = 4R2 in the denominator here. Two stars, each of mass M, form a binary system. The stars orbit about a point a distance R from the center of each star, as shown in the diagram above. The stars themselves each have radius r. Question 65.. In terms of each star's tangential speed v, what is the centripetal acceleration of each star? Answer E—In the centripetal acceleration equation the distance used is the radius of the circular motion. Here, because the planets orbit around a point right in between them, this distance is simply R. Question 76.. A Space Shuttle orbits Earth 300 km above the surface. Why can't the Shuttle orbit 10 km above Earth? (A) The Space Shuttle cannot go fast enough to maintain such an orbit. (B) Kepler's Laws forbid an orbit so close to the surface of the Earth. (C) Because r appears in the denominator of Newton's law of gravitation, the force of gravity is much larger closer to the Earth; this force is too strong to allow such an orbit.
    [Show full text]
  • Trending of SNPP Ephemeris and Its Implications on VIIRS Geometric Performance
    https://ntrs.nasa.gov/search.jsp?R=20170002666 2019-08-31T16:55:42+00:00Z View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NASA Technical Reports Server Trending of SNPP ephemeris and its implications on VIIRS geometric performance Guoqing (Gary) Lin*,a,b, Robert E. Wolfeb, James C. Tiltonc aScience Systems and Applications, Inc., 10210 Greenbelt Road, Lanham, MD, USA 20706; bNASA Goddard Space Flight Center, Code 619, 8800 Greenbelt Rd, Greenbelt, MD, USA 20771; cNASA Goddard Space Flight Center, Code 606, 8800 Greenbelt Rd, Greenbelt, MD, USA 20771 ABSTRACT This paper describes trends in the Suomi National Polar‐orbiting Partnership (SNPP) spacecraft ephemeris data over the four and half years of on-orbit operations. It then discusses the implications of these trends on the geometric performance of the Visible Infrared Imaging Radiometer Suite (VIIRS), one of the instruments onboard SNPP. The SNPP ephemeris data includes time stamped spacecraft positions and velocities that are used to calculate the spacecraft altitude and sub-satellite locations. Through drag make-up maneuvers (DMUs) the orbital mean altitude (spacecraft altitude averaged over an orbit) has been maintained at 838.8 km to within +/- 0.2 km and the orbital period at 101.5 minutes to within +/- 0.2 seconds. The corresponding orbital mean velocity in the terrestrial frame of reference has been maintained at 7524 m/s to within +/- 0.5 m/s. Within an orbit, the altitude varies from 828 km near 15° N to 856 km near the South Pole. Inclination adjust maneuvers (IAMs) have maintained the orbit inclination angle at 98.67° to with +/- 0.07° and the sun-synchronous local time at ascending node (LTAN) at 13:28 to within +/- 5 minutes.
    [Show full text]
  • ORBIT MANOUVERS • Orbital Plane Change (Inclination) It Is an Orbital
    UNIVERSITY OF ANBAR ADVANCED COMMUNICATIONS SYSTEMS FOR 4th CLASS STUDENTS COLLEGE OF ENGINEERING by: Dr. Naser Al-Falahy ELECTRICAL ENGINEERING WE EK 4 ORBIT MANOUVERS Orbital plane change (inclination) It is an orbital maneuver aimed at changing the inclination of an orbiting body's orbit. This maneuver is also known as an orbital plane change as the plane of the orbit is tipped. This maneuver requires a change in the orbital velocity vector (delta v) at the orbital nodes (i.e. the point where the initial and desired orbits intersect, the line of orbital nodes is defined by the intersection of the two orbital planes). In general, inclination changes can take a very large amount of delta v to perform, and most mission planners try to avoid them whenever possible to conserve fuel. This is typically achieved by launching a spacecraft directly into the desired inclination, or as close to it as possible so as to minimize any inclination change required over the duration of the spacecraft life. When both orbits are circular (i.e. e = 0) and have the same radius the Delta-v (Δvi) required for an inclination change (Δvi) can be calculated using: where: v is the orbital velocity and has the same units as Δvi (Δi ) inclination change required. Example Calculate the velocity change required to transfer a satellite from a circular 600 km orbit with an inclination of 28 degrees to an orbit of equal size with an inclination of 20 degrees. SOLUTION, r = (6,378.14 + 600) × 1,000 = 6,978,140 m , ϑ = 28 - 20 = 8 degrees Vi = SQRT[ GM / r ] Vi = SQRT[ 3.986005×1014 / 6,978,140 ] Vi = 7,558 m/s Δvi = 2 × Vi × sin(ϑ/2) Δvi = 2 × 7,558 × sin(8/2) Δvi = 1,054 m/s 18 UNIVERSITY OF ANBAR ADVANCED COMMUNICATIONS SYSTEMS FOR 4th CLASS STUDENTS COLLEGE OF ENGINEERING by: Dr.
    [Show full text]