Musical Notes

Total Page：16

File Type：pdf, Size：1020Kb

Musical Notes Due to the physical principals governing the sound generated by vibrating strings or columns of air in wind instruments, tones of simple instruments consist principally of a fundamental frequency and its harmonics, with the perceived pitch normally the fundamental. (The fundamental is often called the ﬁrst harmonic.) As in many of the examples of Fourier series you've seen, it's common for the fundamental to have the highest power. But this is not necessarily the case for music signals in general. Wind instruments and the human voice in many cases have far greater energy concentrated in upper harmonics than at the fundamental, especially when producing notes near the low end of the instrument's range. According to A. Woods' The Physics of Music, a French horn playing C at 130 Hz, one octave below middle C, is measured as having 1%, 19%, 21%, 48%, 4%, 5%, and 2% of its energy in the fundamental through 7th harmonics, respectively. A bassoon may have its largest energy as high as the sixth harmonic when it reaches a low note, which is why, although you think you hear a really low pitch coming from the bassoon, somehow it just doesn't sound nearly as low as if the same note were played on, for example, a pipe organ. Keep these ideas in mind as you spectrally analyze your music. The pitch corresponding to a particular letter in the range A-G doubles each time we move up an octave. Because there are 12 (even-tempered) \half-steps" in an octave, each step up to an adjacent note on the piano represents a logarithmically equivalent increase by a factor 21=12. The notes of a single octave starting at middle C are approximately as follows: Note Frequency (Hz) C 262 C]=D[ 277 D 294 D]=E[ 311 E 330 F 349 F ]=G[ 370 G 392 G]=A[ 415 A 440 A]=B[ 466 B 494 C 523.

Copy Link

Recommended publications

GRAMMAR of SOLRESOL Or the Universal Language of François SUDRE
GRAMMAR OF SOLRESOL or the Universal Language of François SUDRE by BOLESLAS GAJEWSKI, Professor [M. Vincent GAJEWSKI, professor, d. Paris in 1881, is the father of the author of this Grammar. He was for thirty years the president of the Central committee for the study and advancement of Solresol, a committee founded in Paris in 1869 by Madame SUDRE, widow of the Inventor.] [This edition from taken from: Copyright © 1997, Stephen L. Rice, Last update: Nov. 19, 1997 URL: http://www2.polarnet.com/~srice/solresol/sorsoeng.htm Edits in [brackets], as well as chapter headings and formatting by Doug Bigham, 2005, for LIN 312.] I. Introduction II. General concepts of solresol III. Words of one [and two] syllable[s] IV. Suppression of synonyms V. Reversed meanings VI. Important note VII. Word groups VIII. Classification of ideas: 1º simple notes IX. Classification of ideas: 2º repeated notes X. Genders XI. Numbers XII. Parts of speech XIII. Number of words XIV. Separation of homonyms XV. Verbs XVI. Subjunctive XVII. Passive verbs XVIII. Reflexive verbs XIX. Impersonal verbs XX. Interrogation and negation XXI. Syntax XXII. Fasi, sifa XXIII. Partitive XXIV. Different kinds of writing XXV. Different ways of communicating XXVI. Brief extract from the dictionary I. Introduction In all the business of life, people must understand one another. But how is it possible to understand foreigners, when there are around three thousand different languages spoken on earth? For everyone's sake, to facilitate travel and international relations, and to promote the progress of beneficial science, a language is needed that is easy, shared by all peoples, and capable of serving as a means of interpretation in all countries.
[Show full text]
10 - Pathways to Harmony, Chapter 1
Pathways to Harmony, Chapter 1. The Keyboard and Treble Clef Chapter 2. Bass Clef In this chapter you will: 1.Write bass clefs 2. Write some low notes 3. Match low notes on the keyboard with notes on the staff 4. Write eighth notes 5. Identify notes on ledger lines 6. Identify sharps and flats on the keyboard 7.Write sharps and flats on the staff 8. Write enharmonic equivalents date: 2.1 Write bass clefs • The symbol at the beginning of the above staff, , is an F or bass clef. • The F or bass clef says that the fourth line of the staff is the F below the piano’s middle C. This clef is used to write low notes. DRAW five bass clefs. After each clef, which itself includes two dots, put another dot on the F line. © Gilbert DeBenedetti - 10 - www.gmajormusictheory.org Pathways to Harmony, Chapter 1. The Keyboard and Treble Clef 2.2 Write some low notes •The notes on the spaces of a staff with bass clef starting from the bottom space are: A, C, E and G as in All Cows Eat Grass. •The notes on the lines of a staff with bass clef starting from the bottom line are: G, B, D, F and A as in Good Boys Do Fine Always. 1. IDENTIFY the notes in the song “This Old Man.” PLAY it. 2. WRITE the notes and bass clefs for the song, “Go Tell Aunt Rhodie” Q = quarter note H = half note W = whole note © Gilbert DeBenedetti - 11 - www.gmajormusictheory.org Pathways to Harmony, Chapter 1.
[Show full text]
Unicode Technical Note: Byzantine Musical Notation
1 Unicode Technical Note: Byzantine Musical Notation Version 1.0: January 2005 Nick Nicholas; [email protected] This note documents the practice of Byzantine Musical Notation in its various forms, as an aid for implementors using its Unicode encoding. The note contains a good deal of background information on Byzantine musical theory, some of which is not readily available in English; this helps to make sense of why the notation is the way it is.1 1. Preliminaries 1.1. Kinds of Notation. Byzantine music is a cover term for the liturgical music used in the Orthodox Church within the Byzantine Empire and the Churches regarded as continuing that tradition. This music is monophonic (with drone notes),2 exclusively vocal, and almost entirely sacred: very little secular music of this kind has been preserved, although we know that court ceremonial music in Byzantium was similar to the sacred. Byzantine music is accepted to have originated in the liturgical music of the Levant, and in particular Syriac and Jewish music. The extent of continuity between ancient Greek and Byzantine music is unclear, and an issue subject to emotive responses. The same holds for the extent of continuity between Byzantine music proper and the liturgical music in contemporary use—i.e. to what extent Ottoman inﬂuences have displaced the earlier Byzantine foundation of the music. There are two kinds of Byzantine musical notation. The earlier ecphonetic (recitative) style was used to notate the recitation of lessons (readings from the Bible). It probably was introduced in the late 4th century, is attested from the 8th, and was increasingly confused until the 15th century, when it passed out of use.
[Show full text]
Major and Minor Scales Half and Whole Steps
Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale.
[Show full text]
Generalized Interval System and Its Applications
Generalized Interval System and Its Applications Minseon Song May 17, 2014 Abstract Transformational theory is a modern branch of music theory developed by David Lewin. This theory focuses on the transformation of musical objects rather than the objects them- selves to find meaningful patterns in both tonal and atonal music. A generalized interval system is an integral part of transformational theory. It takes the concept of an interval, most commonly used with pitches, and through the application of group theory, generalizes beyond pitches. In this paper we examine generalized interval systems, beginning with the definition, then exploring the ways they can be transformed, and finally explaining com- monly used musical transformation techniques with ideas from group theory. We then apply the the tools given to both tonal and atonal music. A basic understanding of group theory and post tonal music theory will be useful in fully understanding this paper. Contents 1 Introduction 2 2 A Crash Course in Music Theory 2 3 Introduction to the Generalized Interval System 8 4 Transforming GISs 11 5 Developmental Techniques in GIS 13 5.1 Transpositions . 14 5.2 Interval Preserving Functions . 16 5.3 Inversion Functions . 18 5.4 Interval Reversing Functions . 23 6 Rhythmic GIS 24 7 Application of GIS 28 7.1 Analysis of Atonal Music . 28 7.1.1 Luigi Dallapiccola: Quaderno Musicale di Annalibera, No. 3 . 29 7.1.2 Karlheinz Stockhausen: Kreuzspiel, Part 1 . 34 7.2 Analysis of Tonal Music: Der Spiegel Duet . 38 8 Conclusion 41 A Just Intonation 44 1 1 Introduction David Lewin(1933 - 2003) is an American music theorist.
[Show full text]
Tools-For-Tosafos-Selections.Pdf
wffiffiLs FOR w &F F$af,m Per$mutter T.AR G UI\,{,/F.E LD }-{ ts N N4 $sltroducttost Whot trs Tosef'os? Tosafos is a collection of the interpretations and explana- tions of the Gemara by the group of sages known as "baalei haTosdos," i.e., the Tosafos masters. Tt:re baalei haTosafos (also known as "Tosafists") were sages of theJewish communities in France and Germany (with a few in other European countries) in the twelfth and thirteenth centuries. Some of them offici- ated as the halachic leaders of the community and functioned as representatives to the gentile authorities. Some ranyeshivos, where disciples would devote all their time to studying Torah. ThebaaleihaTosafoslived in a time that is regarded inJewish history as the period of the Rishonim. "Rishonirn" (literally "first") is the collective term given to the sages who lived in Europe and North Africa after the time of the Geonim (who lived in Babylon). This period extended until the Tur or R' Yosef Karo (who compiled the Shulchan Aruch), after which the period of the Acharonim began. Not all the sages who lived in these areas during this time period are called Tosafists, however. The term "Tosafist" applies to those who learned the Gemara in a certain way. The way th,e baalei haTosafos learned is, in effect, the focus of this work. 1Z Tools for Tosafos Introrttacn-ion 13 a sage who constantly compated At this poin! we can say that Sirece then, mrost prlntirags of the Taknud have contained differences in the Talmudic text, -W?t-{sa'l'{ and attempted to consolidate Tcsafcs's c*lrlmentar)'.
[Show full text]
The Chromatic Scale
Getting to Know Your Guitar: The Chromatic Scale Your Guitar is designed as a chromatic instrument – that is, guitar frets represent chromatic “semi- tones” or “half-steps” up and down the guitar fretboard. This enables you to play scales and chords in any key, and handle pretty much any music that comes from the musical traditions of the Western world. In this sense, the chromatic scale is more foundational than it is useful as a soloing tool. Put another way, almost all of the music you will ever play will be made interesting not by the use of the chromatic scale, but by the absence of many of the notes of the chromatic scale! All keys, chords, scales, melodies and harmonies, could be seen simply the chromatic scale minus some notes. For all the examples that follow, play up and down (both ascending and descending) the fretboard. Here is what you need to know in order to understand The Chromatic Scale: 1) The musical alphabet contains 7 letters: A, B, C, D, E, F, G. The notes that are represented by those 7 letters we will call the “Natural” notes 2) There are other notes in-between the 7 natural notes that we’ll call “Accidental” notes. They are formed by taking one of the natural notes and either raising its pitch up, or lowering its pitch down. When we raise a note up, we call it “Sharp” and use the symbol “#” after the note name. So, if you see D#, say “D sharp”. When we lower the note, we call it “Flat” and use the symbol “b” after the note.
[Show full text]
Musical Elements in the Discrete-Time Representation of Sound
0 Musical elements in the discrete-time representation of sound RENATO FABBRI, University of Sao˜ Paulo VILSON VIEIRA DA SILVA JUNIOR, Cod.ai ANTONIOˆ CARLOS SILVANO PESSOTTI, Universidade Metodista de Piracicaba DEBORA´ CRISTINA CORREA,ˆ University of Western Australia OSVALDO N. OLIVEIRA JR., University of Sao˜ Paulo e representation of basic elements of music in terms of discrete audio signals is oen used in soware for musical creation and design. Nevertheless, there is no unied approach that relates these elements to the discrete samples of digitized sound. In this article, each musical element is related by equations and algorithms to the discrete-time samples of sounds, and each of these relations are implemented in scripts within a soware toolbox, referred to as MASS (Music and Audio in Sample Sequences). e fundamental element, the musical note with duration, volume, pitch and timbre, is related quantitatively to characteristics of the digital signal. Internal variations of a note, such as tremolos, vibratos and spectral uctuations, are also considered, which enables the synthesis of notes inspired by real instruments and new sonorities. With this representation of notes, resources are provided for the generation of higher scale musical structures, such as rhythmic meter, pitch intervals and cycles. is framework enables precise and trustful scientic experiments, data sonication and is useful for education and art. e ecacy of MASS is conrmed by the synthesis of small musical pieces using basic notes, elaborated notes and notes in music, which reects the organization of the toolbox and thus of this article. It is possible to synthesize whole albums through collage of the scripts and seings specied by the user.
[Show full text]
Chromatic Fingering Chart for Euphonium T.C
Chromatic Fingering Chart for Euphonium T.C. Note: Only the most commonly used fingerings are listed here, in order of preference. The overtone chart available on this website provides comprehensive information about available alternate fingerings. The differing fingerings for certain lower-register notes on compensating versus non-compensating instruments are clearly indicated. All sounding pitches are a major ninth lower than written. G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & w #w bw w #w bw w w Ÿ ◊ 1 (false tone) 2 (false tone) 2-4 (false tone) 4 (false tone) 2-3 (false tone) 1-2 (false tone) 1-2-3 (false tone) 1-3 (false tone) C-Sharp or D-Flat D-Sharp or E-Flat F-Sharp or G-Flat (Concert B or C-Flat) D (Concert C) (Concert C-Sharp or D-Flat) E (Concert D) F (Concert E-Flat) (Concert E or F-Flat) & #w bw w #w bw w w #w bw “C‘ompensating: Compensating: Compensating: Compensating: Compensating: 2-4 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 1-2-3 Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: 1-2-3-4 (false tone) 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & w #w bw w #w bw w w “4‘ 2-3 1-2 1 2 0 1-3 3 C-Sharp or D-Flat D-Sharp or E-Flat F-Sharp or G-Flat (Concert B or C-Flat) D (Concert C) (Concert C-Sharp or D-Flat) E (Concert D) F (Concert E-Flat) (Concert E or F-Flat) & bw #w bw w #w bw w w #w2-4 Compensating: Compensating: Compensating: Compensating: Compensating: 1-2-3 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: Non-Compensating: 1-2-3-4 (false tone) 1-2-3-4 1-3-4 2-3-4 1-2-4 1-4 G-Sharp or A-Flat A-Sharp or B-Flat G (Concert F) A (Concert G) B (Concert A) C (Concert B-Flat) (Concert F-Sharp or G-Flat) (Concert G-Sharp or A-Flat) & bw w w w4 #w2-3 bw w1-2 #w1 2 0 1-3 3 1-4 2 Chromatic Fingering Chart for Euphonium T.C.
[Show full text]
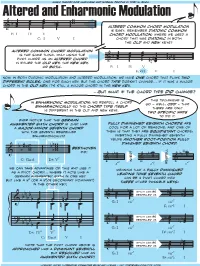
Altered and Enharmonic Modulation
Altered andmusic Enharmonictheory for musicians and normal people Modulation by toby w. rush œ œ w b œ œ œ nœ w Altered common chord modulation & œ œ is easy: remember diatonic common F: I IV V chord modulation, where we used a C: I V I chord that was diatonic in both the old and new keys? altered common chord modulation is the same thing, only using the œ œ pivot chord as an altered chord & b œ œ œ #nw in either the old key, the new key, œ # #œ w or both. F: I IV V n œ E: bVI V I Now, in both diatonic modulation and altered modulation, we have one chord that plays two different roles, one for each key. But the chord type doesn’t change... if it was a major chord in the old key, it’s still a major chord in the new key. ...but...but whatwhat ifif thethe chordchord typetype did change? this technique is in enharmonic modulation, we respell a chord so — well, odd — that so the enharmonically chord type itself there are only is different in the old and new keys. two specific ways to do it. ever notice that the german augmented sixth chord is just like fully diminished seventh chords are a major-minor seventh chord cool for a lot of reasons, and one of with the seventh respelled them is that they are equidistant chords: enharmonically? inverting a fully diminshed seventh yields another root-position fully dimished seventh chord. # w bw beethoven b ww b w did! & b w bw bw bww b ∫w 7 b w C: Ger.6 D : V b w b w w b & w7 invert & 6 & 7 a° a°5 respell c° we can take advantage of this and use it meaning that a fully diminished as a pivot chord..
[Show full text]
Music Representations
Lecture Music Processing Music Representations Meinard Müller International Audio Laboratories Erlangen [email protected] Book: Fundamentals of Music Processing Meinard Müller Fundamentals of Music Processing Audio, Analysis, Algorithms, Applications 483 p., 249 illus., hardcover ISBN: 978-3-319-21944-8 Springer, 2015 Accompanying website: www.music-processing.de Book: Fundamentals of Music Processing Meinard Müller Fundamentals of Music Processing Audio, Analysis, Algorithms, Applications 483 p., 249 illus., hardcover ISBN: 978-3-319-21944-8 Springer, 2015 Accompanying website: www.music-processing.de Book: Fundamentals of Music Processing Meinard Müller Fundamentals of Music Processing Audio, Analysis, Algorithms, Applications 483 p., 249 illus., hardcover ISBN: 978-3-319-21944-8 Springer, 2015 Accompanying website: www.music-processing.de Chapter 1: Music Representations 1.1 Sheet Music Representations 1.2 Symbolic Representations 1.3 Audio Representation 1.4 Further Notes Musical information can be represented in many different ways. In Chapter 1, we consider three widely used music representations: sheet music, symbolic, and audio representations. This first chapter also introduces basic terminology that is used throughout the book. In particular, we discuss musical and acoustic properties of audio signals including aspects such as frequency, pitch, dynamics, and timbre. Music Representations Music Representations . Sheet music representation visual description of a musical score image format (printed or scanned) . Symbolic representations description based on entities with explicit musical meaning given in digital format that can be parsed by a computer . Audio representation physical description encoding of sound wave Sheet Music Representation . Graphical-textual encoding of musical parameters notes (onsets, pitches, durations) tempo, measure, dynamics instrumentation … .
[Show full text]
The Consecutive-Semitone Constraint on Scalar Structure: a Link Between Impressionism and Jazz1
The Consecutive-Semitone Constraint on Scalar Structure: A Link Between Impressionism and Jazz1 Dmitri Tymoczko The diatonic scale, considered as a subset of the twelve chromatic pitch classes, possesses some remarkable mathematical properties. It is, for example, a "deep scale," containing each of the six diatonic intervals a unique number of times; it represents a "maximally even" division of the octave into seven nearly-equal parts; it is capable of participating in a "maximally smooth" cycle of transpositions that differ only by the shift of a single pitch by a single semitone; and it has "Myhill's property," in the sense that every distinct two-note diatonic interval (e.g., a third) comes in exactly two distinct chromatic varieties (e.g., major and minor). Many theorists have used these properties to describe and even explain the role of the diatonic scale in traditional tonal music.2 Tonal music, however, is not exclusively diatonic, and the two nondiatonic minor scales possess none of the properties mentioned above. Thus, to the extent that we emphasize the mathematical uniqueness of the diatonic scale, we must downplay the musical significance of the other scales, for example by treating the melodic and harmonic minor scales merely as modifications of the natural minor. The difficulty is compounded when we consider the music of the late-nineteenth and twentieth centuries, in which composers expanded their musical vocabularies to include new scales (for instance, the whole-tone and the octatonic) which again shared few of the diatonic scale's interesting characteristics. This suggests that many of the features *I would like to thank David Lewin, John Thow, and Robert Wason for their assistance in preparing this article.
[Show full text]