A Taste of Haskell
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Vorlesung-Print.Pdf
1 Betriebssysteme Prof. Dipl.-Ing. Klaus Knopper (C) 2019 <[email protected]> Live GNU/Linux System Schwarz: Transparent,KNOPPIX CD−Hintergrundfarbe (silber) bei Zweifarbdruck, sonst schwarz. Vorlesung an der DHBW Karlsruhe im Sommersemester 2019 Organisatorisches + Vorlesung mit Ubungen¨ Betriebssysteme WWI17B2 jeweils Montags (einzelne Termine) in A369 + http://knopper.net/bs/ (spater¨ moodle) Folie 1 Kursziel µ Grundsatzlichen¨ Aufbau von Betriebssystemen in Theorie und Praxis kennen und verstehen, µ grundlegende Konzepte von Multitasking, Multiuser-Betrieb und Hardware-Unterstutzung¨ / Resource-Sharing erklaren¨ konnen,¨ µ Sicherheitsfragen und Risiken des Ubiquitous und Mobile Computing auf Betriebssystemebene analysieren, µ mit heterogenen Betriebssystemumgebungen und Virtua- lisierung arbeiten, Kompatibilitatsprobleme¨ erkennen und losen.¨ Folie 2 0 Themen (Top-Down) + Ubersicht¨ Betriebssysteme und Anwendungen, Unterschiede in Aufbau und Einsatz, Lizenzen, Distributionen, + GNU/Linux als OSS-Lernsystem fur¨ die Vorlesung, Tracing und Analyse des Bootvorgangs, + User Interface(s), + Dateisystem: VFS, reale Implementierungen, + Multitasking: Scheduler, Interrupts, Speicherverwaltung (VM), Prozessverwaltung (Timesharing), + Multiuser: Benutzerverwaltung, Rechtesystem, + Hardware-Unterstutzung:¨ Kernel und Module vs. Treiber“ - Kon- ” zept, + Kompatibilitat,¨ API-Emulation, Virtualisierung, Softwareentwick- lung. + Sicherheits-Aspekte von Betriebssystemen, Schadsoftware“ und ” forensische Analyse bei Kompromittierung oder Datenverlust. -

New Brunswick Man Charged in Burglary Cording to Police
Preserving the past Racin' with the best Nine Middlesex County farms are on their Winston Cup stars compete at New Egypt way to being preserved Speedway Page 3 Page 22 Serving North and South Brunswick August 29, 20 fww.gmnew New Brunswick man charged in burglary cording to police. No. Bruns. homeowner Saloom said police heard a commotion injured in struggle with once they entered the residence and rushed up the stairs. alleged home invader Yosko was found struggling with Gar- BY PAVE GOLDBERG rard on the bathroom floor, according to Staff Writer police. "Yosko was waiting for the police to New Brunswick man has been arrive at the time," Saloom said. "Both arrested after police say he was males were covered in blood." A caught in the act of burglarizing a Garrard resisted police when they tried North Brunswick home. to arrest him, according to Saloom. Hassan K. Garrard, 22, of New "The officers attempted to subdue him, Brunswick was arrested and charged with but he was resisting and would not submit burglary, aggravated assault and resisting his hands for arrest after numerous verbal arrest during an alleged burglary at a resi- commands to release his hands from his dence on Noah Drive at 1:02 a.m. Aug. 22. chest," Saloom said. "There was a piece of "We came on Ihc call of a burglary in broken glass in his hand, and he refused to progress," said North Brunswick Detective release it despite numerous requests." George Saloom. "Upon arrival, a woman Saloom said the officers were forced to alerted the officers on the scene that her use pepper spray on Garrard. -

Suckless.Org Software That Sucks Less
suckless.org software that sucks less markus schnalke <[email protected]> a website a couple of projects a community a philosophy . not a summary, but we’ll have one at the end what is suckless.org? something that Anselm R. Garbe started a couple of projects a community a philosophy . not a summary, but we’ll have one at the end what is suckless.org? something that Anselm R. Garbe started a website a community a philosophy . not a summary, but we’ll have one at the end what is suckless.org? something that Anselm R. Garbe started a website a couple of projects a philosophy . not a summary, but we’ll have one at the end what is suckless.org? something that Anselm R. Garbe started a website a couple of projects a community . not a summary, but we’ll have one at the end what is suckless.org? something that Anselm R. Garbe started a website a couple of projects a community a philosophy what is suckless.org? something that Anselm R. Garbe started a website a couple of projects a community a philosophy . not a summary, but we’ll have one at the end the website website www.suckless.org main page (links to everything else) lists.suckless.org the mailinglists archives code.suckless.org the source code repositories (Mercurial) the wiki the wiki software I hgiki (genosite) I self made by arg I shell script with 100 SLOC I uses markdown markup content I kept in Mercurial repo I write access to preview wiki (port 8000) I hg clone http://www.suckless.org:8000/hg/wiki I vi <some-file> I hg commit && hg push the couple of projects projects window managers I wmii I dwm IRC clients I sic I ii various tools I dmenu, slock, sselp, lsx, . -

Betriebssysteme
Betriebssysteme Prof. Dipl.-Ing. Klaus Knopper (C) 2019 <[email protected]> Live GNU/Linux System Schwarz: Transparent,KNOPPIX CD−Hintergrundfarbe (silber) bei Zweifarbdruck, sonst schwarz. Vorlesung an der DHBW Karlsruhe im Sommersemester 2019 •First •Prev •Next •Last •Full Screen •Quit Organisatorisches + Vorlesung mit Ubungen¨ Betriebssysteme WWI17B2 jeweils Montags (einzelne Termine) in A369 + http://knopper.net/bs/ (spater¨ moodle) •First •Prev •Next •Last Folie 1 •Full Screen •Quit Kursziel µ Grundsatzlichen¨ Aufbau von Betriebssystemen in Theorie und Praxis kennen und verstehen, µ grundlegende Konzepte von Multitasking, Multiuser-Betrieb und Hardware-Unterstutzung¨ / Resource-Sharing erklaren¨ konnen,¨ µ Sicherheitsfragen und Risiken des Ubiquitous und Mobile Computing auf Betriebssystemebene analysieren, µ mit heterogenen Betriebssystemumgebungen und Virtua- lisierung arbeiten, Kompatibilitatsprobleme¨ erkennen und losen.¨ •First •Prev •Next •Last Folie 2 •Full Screen •Quit Themen (Top-Down) + Ubersicht¨ Betriebssysteme und Anwendungen, Unterschiede in Aufbau und Einsatz, Lizenzen, Distributionen, + GNU/Linux als OSS-Lernsystem fur¨ die Vorlesung, Tracing und Analyse des Bootvorgangs, + User Interface(s), + Dateisystem: VFS, reale Implementierungen, + Multitasking: Scheduler, Interrupts, Speicherverwaltung (VM), Prozessverwaltung (Timesharing), + Multiuser: Benutzerverwaltung, Rechtesystem, + Hardware-Unterstutzung:¨ Kernel und Module vs. Treiber“ - Kon- ” zept, + Kompatibilitat,¨ API-Emulation, Virtualisierung, Softwareentwick- -

Linux-Cookbook.Pdf
LINUX COOKBOOK ™ Other Linux resources from O’Reilly Related titles Linux Device Drivers Exploring the JDS Linux Linux in a Nutshell Desktop Running Linux Learning Red Hat Enterprise Building Embedded Linux Linux and Fedora Systems Linux Pocket Guide Linux Security Cookbook Understanding the Linux Kernel Linux Books linux.oreilly.com is a complete catalog of O’Reilly’s books on Resource Center Linux and Unix and related technologies, including sample chapters and code examples. ONLamp.com is the premier site for the open source web plat- form: Linux, Apache, MySQL, and either Perl, Python, or PHP. Conferences O’Reilly brings diverse innovators together to nurture the ideas that spark revolutionary industries. We specialize in document- ing the latest tools and systems, translating the innovator’s knowledge into useful skills for those in the trenches. Visit conferences.oreilly.com for our upcoming events. Safari Bookshelf (safari.oreilly.com) is the premier online refer- ence library for programmers and IT professionals. Conduct searches across more than 1,000 books. Subscribers can zero in on answers to time-critical questions in a matter of seconds. Read the books on your Bookshelf from cover to cover or sim- ply flip to the page you need. Try it today with a free trial. LINUX COOKBOOK ™ Carla Schroder Beijing • Cambridge • Farnham • Köln • Paris • Sebastopol • Taipei • Tokyo Linux Cookbook™ by Carla Schroder Copyright © 2005 O’Reilly Media, Inc. All rights reserved. Printed in the United States of America. Published by O’Reilly Media, Inc., 1005 Gravenstein Highway North, Sebastopol, CA 95472. O’Reilly books may be purchased for educational, business, or sales promotional use. -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae -

Knowing Knoppix/Print Version - Wikibooks, Open Books for an Open World
Knowing Knoppix/Print version - Wikibooks, open books for an open world Knowing Knoppix/Print version Knowing Knoppix The current, editable version of this book is available in Wikibooks, the open-content textbooks collection, at http://en.wikibooks.org/wiki/Knowing_Knoppix Permission is granted to copy, distribute, and/or modify this document under the terms of the Creative Commons Attribution-ShareAlike 3.0 License. Contents 1 Introducing Knoppix 1.1 Introducing Knoppix 1.1.1 What is Knoppix? 1.1.1.1 Linux that runs from CD 1.1.1.2 Can be installed on a Hard Disk or a USB key 1.1.1.3 How it works 1.1.1.4 Safe to run 1.1.1.5 Personal 1.1.1.6 Free 1.1.2 What you can do with Knoppix 1.1.2.1 Learn Linux 1.1.2.2 Rescue and test 1.1.2.3 Use and explore 1.1.2.4 Network 1.1.3 Where Knoppix comes from 1.1.4 Knoppix is Free Software 1.1.5 Limitations 1.1.5.1 No warranty 1.1.5.2 CD means slow 1.1.5.3 Not everything works 1 von 71 Knowing Knoppix/Print version - Wikibooks, open books for an open world 1.1.5.4 RAM intensive 1.1.6 What is included in Knoppix? 1.1.7 What is Linux? 1.1.7.1 A little history 1.1.7.1.1 How GNU grew 1.1.7.1.2 It's a GNU world! 2 Knoppix for the first time 2.1 Knoppix for the first time 2.1.1 Overview 2.1.2 Hardware requirements 2.1.3 Starting Knoppix 2.1.3.1 The first stage 2.1.3.2 The second stage 2.1.4 The first stage 2.1.4.1 Getting to the boot prompt 2.1.4.2 Help at the boot prompt 2.1.4.2.1 Quick help 2.1.5 The second stage 2.1.5.1 Starting Knoppix proper 2.1.5.2 Which keyboard/language? 2.1.5.3 Automatic hardware detection -

Warmair SWF, 46..5'9", Shapely
a!fj¥*™.W-ti15^r"55^^*S*^,^?f!ri^^ k~j-:;d(\ ''''.'•)• [y ••''••• •.".•'••V1 '::~"::'':':-\:: y"< •.•''•-.;':•;-;' '•' ;''£ .-,..;• .•'•;.. ,"•'-•'.'•,'•,. •':'"''••"'••••'.;i -.••"•• •'' :'•'';': "••' 'v '••'•••• .';i:-'.::.''''; ••"•••.•'•:'"'- • '^'^^••x,./'-^ .;:;•"7y":v:-•:•' ,'•: r'/•••••'.•'.':"-:^-J':'••'/!•'• :•••'-.'- ''.:•""'.' ;.''••'•.':' • :-"-'-"''i\'-i-''.'' Cranford Chronicle j '• ' • •I •'.•;. •'. I ford Chronicle, the areas best source for local news, call (800) 300-9321 w.edfct To place • ' 1 _*. _i> % . _^k M H' "•••'.: To respond to ads, call _____J10.Nb.3 | CRANFORD » GARWOdD » KENILWORTH Thursday; JanuSiry 1.5,1998 C 50 cents ; ifeAEFRE9MQ. : .- ; •. '• '••' '• .•'. • •' .-• • ITALIAN BROWN EYES . ..•'• '•:• , :• ••'. ., .': AMUAI.LOVER HAN OF COMPLIANCE. '' '. ..'.' '!• , :". .-..;. -HELP r-. .1U, goigadia bhnMla SMtF.iso.edmaM P. ff.*. joimg «_<.• ' Atlractlve. cully brmm-haJrad SWPF, 35.5'4-, looking fof attrac- Firiess (orrpsnlon wanted; OWF lefts DWMj'4Si5, for match' - And devotion. Gentle, lald-baclr. Onsefish PM, 4O8."Seek! PF, cre- Attractive, naive. mW-Westem SWPM, 31, attrfl*ejDici«a?«W Women seeking a tnm, ccl«glil«, flnandafy team, fun-lovlnj commimlcalor, en/ ' llvo.conpfflWo SWPM.SWO, to care tor, travel wltti, have fun.' Ir^twemiUoutsitttarjyr^musi'ltecats.Arjl.8026., ,' ' atfve, enterprising, strong-willed, for, committed, binding relation- • ISO. Jersey girt to show me dtytfe and intense conversation, Ad»! : . joys toB ot totfCfTiuas.'AtH 6248. "••;',"• .'•.'...•'•'.*•''• wilh.-AUI.8437' . '. -

Running KNOPPIX 331
18_579495 ch11.qxd 12/27/04 10:09 PM Page 329 CHAPTER Running 1111 KNOPPIX ✦✦✦✦ In This Chapter Understanding computer’s operating system usually resides on the KNOPPIX A hard disk — but it doesn’t have to. When a computer boots up, it typically checks first if there is a CD, floppy disk, Starting KNOPPIX or DVD in a drive and tries to boot from there (depending on BIOS settings). So, with up to 700MB (CD) or 4.7GB (DVD) of space on those media, why not use them to boot whole oper- Using KNOPPIX ating systems? ✦✦✦✦ Well, that’s exactly what bootable Linux distributions (also called live CDs) such as KNOPPIX do. In the case of KNOPPIX, one CD holds up to 2GB of compressed software for you to run that uncompresses on-the-fly. Start it up and you can try out all the features of a well-stocked Linux system, without touching the contents of your hard disk. On the KNOPPIX is included on the DVD that comes with this book. DVD-ROM In fact, it is the default option. Insert the DVD into your PC’s DVD drive and, when you see the boot screen, press Enter. KNOPPIX should just start up, and you can begin using it as described in this chapter. If you have never used Linux before, KNOPPIX gives you the chance to do so in a very safe way. If you are experienced with Linux, KNOPPIX can be used as a tool to take Linux with you everywhere, troubleshoot a computer, or check if a computer will run Linux. -

O'reilly Knoppix Hacks (2Nd Edition).Pdf
SECOND EDITION KNOPPIX HACKSTM Kyle Rankin Beijing • Cambridge • Farnham • Köln • Paris • Sebastopol • Taipei • Tokyo Knoppix Hacks,™ Second Edition by Kyle Rankin Copyright © 2008 O’Reilly Media, Inc. All rights reserved. Printed in the United States of America. Published by O’Reilly Media, Inc., 1005 Gravenstein Highway North, Sebastopol, CA 95472. O’Reilly books may be purchased for educational, business, or sales promotional use. Online editions are also available for most titles (safari.oreilly.com). For more information, contact our corporate/institutional sales department: (800) 998-9938 or [email protected]. Editor: Brian Jepson Cover Designer: Karen Montgomery Production Editor: Adam Witwer Interior Designer: David Futato Production Services: Octal Publishing, Inc. Illustrators: Robert Romano and Jessamyn Read Printing History: October 2004: First Edition. November 2007: Second Edition. Nutshell Handbook, the Nutshell Handbook logo, and the O’Reilly logo are registered trademarks of O’Reilly Media, Inc. The Hacks series designations, Knoppix Hacks, the image of a pocket knife, “Hacks 100 Industrial-Strength Tips and Tools,” and related trade dress are trademarks of O’Reilly Media, Inc. Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and O’Reilly Media, Inc. was aware of a trademark claim, the designations have been printed in caps or initial caps. While every precaution has been taken in the preparation of this book, the publisher and author assume no responsibility for errors or omissions, or for damages resulting from the use of the information contained herein. Small print: The technologies discussed in this publication, the limitations on these technologies that technology and content owners seek to impose, and the laws actually limiting the use of these technologies are constantly changing. -

KNOWING KNOPPIX the Beginner's Guide to the Linux That Runs from CD
KNOWING KNOPPIX The beginner's guide to the Linux that runs from CD Phil Jones 1 Copyright (c) 2005 Phil Jones. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”. 2 Table of Contents Introducing Knoppix...............................................................................7 What is Knoppix?...............................................................................7 Linux that runs from CD..............................................................7 How it works..................................................................................7 Safe to run......................................................................................8 Personal..........................................................................................8 Free.................................................................................................8 What you can do with Knoppix.........................................................8 Learn Linux....................................................................................8 Rescue and test..............................................................................9 Use and explore.............................................................................9 Network..........................................................................................9 -
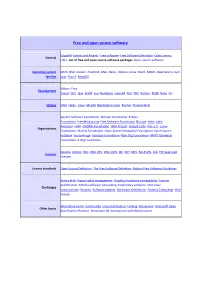
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed