Generalizations and Applications of the Stochastic Block Model to Basketball Games and Variable Selection Problems
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Andrew Lehman Jimmy Durkin Joseph Kelly Adam Sattler
MEET OUR TEAM NFLPA CERTIFIED CONTRACT ADVISORS Free Agent Sports (FAS) is a Licensed, Insured, Registered, Certified, and Bonded Professional Sports Corporation with Offices in Los Angeles, CA, Houston, TX, New York, NY. FAS offers athlete representation and contract negotiation services in Football and Basketball, as well as Athlete & Celebrity Endorsements, Brand Development and Management, Promotional Services & Marketing, and Post Career Financial Services & Planning. FAS Agents have negotiated more than $100,000,000.00 in Professional Sports Contracts (NFL, NBA) and more than $10,000,000.00 in Athlete & Celebrity Endorsements in the past 5 years!! We want you to be the NEXT!!! HERE ARE OUR 4 #FAS PARTNER AGENTS Andrew Lehman Jimmy Durkin Joseph Kelly Adam Sattler FAS Agents Are Licensed in the States of Illinois, Idaho, Pennsylvania, New York, New Jersey, Ohio, North Carolina, South Carolina, Texas, Louisiana, Alabama, Texas, California, Georgia, Arizona, and Florida, among others as of 2019. 2600 S. Shore Blvd., Suite 300, League City, TX | 888-519-6525 | [email protected] ANDREW LEHMAN NFLPA CERTIFIED CONTRACT ADVISOR NBPA CERTIFIED CONTRACT ADVISOR Andrew Lehman founded FAS in 2013, in Houston, TX. Now a 6th year licensed NFL Agent, ANDREW LEHMAN is based in Houston (League City) office. Being in Houston allows for Andrew to give special attention to players in Texas. Andrew has NFL in his blood and he has been dealing with NFL his entire life. As part of the Wisniewski family, a football family which spans over three generations, he has seen his fair share of contracts and the possible complications. This is part of the reason that compelled him to get his Law degree and pursue this career as a professional athlete advisor. -

(Wtam, Fsn Oh) 7:00 Pm
SUN., MAY 21, 2017 QUICKEN LOANS ARENA – CLEVELAND, OH TV: TNT RADIO: WTAM 1100/LA MEGA 87.7 FM/ESPN RADIO 8:30 PM ET CLEVELAND CAVALIERS (51-31, 10-0) VS. BOSTON CELTICS (53-29, 8-7) (CAVS LEAD SERIES 2-0) 2016-17 CLEVELAND CAVALIERS GAME NOTES CONFERENCE FINALS GAME 3 OVERALL PLAYOFF GAME # 11 HOME GAME # 5 PROBABLE STARTERS POS NO. PLAYER HT. WT. G GS PPG RPG APG FG% MPG F 23 LEBRON JAMES 6-8 250 16-17: 74 74 26.4 8.6 8.7 .548 37.8 PLAYOFFS: 10 10 34.3 8.5 7.1 .569 41.4 QUARTERFINALS F 0 KEVIN LOVE 6-10 251 16-17: 60 60 19.0 11.1 1.9 .427 31.4 # 2 Cleveland vs. # 7 Indiana PLAYOFFS: 10 10 16.3 9.7 1.4 .459 31.1 CAVS Won Series 4-0 C 13 TRISTAN THOMPSON 6-10 238 16-17: 78 78 8.1 9.2 1.0 .600 30.0 Game 1 at Cleveland; April 15 PLAYOFFS: 10 10 8.9 9.6 1.1 .593 32.1 CAVS 109, Pacers 108 G 5 J.R. SMITH 6-6 225 16-17: 41 35 8.6 2.8 1.5 .346 29.0 Game 2 at Cleveland; April 17 PLAYOFFS: 10 10 6.2 2.4 0.8 .478 25.7 CAVS 117, Pacers 111 Game 3 at Indiana; April 20 G 2 KYRIE IRVING 6-3 193 16-17: 72 72 25.2 3.2 5.8 .473 35.1 PLAYOFFS: 10 10 22.4 2.4 5.5 .415 33.9 CAVS 119, Pacers 114 Game 4 at Indiana; April 23 CAVS 106, Pacers 102 CAVS QUICK FACTS The Cleveland Cavaliers will look to take a 3-0 series lead over the Boston Celtics after posting a 130-86 victory in Game 2 at TD Garden on Wednesday night. -
Willie Nelson Talks Music Legends Same Producers As “300,” Is Just As Bloody but Not Documentary Highlights As Big of a Hit with Some Audiences
WE’RE THERE WHEN YOU CAN’T BE NELSON from Page 1 TheWEDNESDAY | NOVEMBER Baylor 16, 2011 Lariatwww.baylorlariat.com SPORTS Page 5 NEWS Page 3 A&E Page 4 A sweet reunion Baylor green is gold It’s no secret Baylor and the San Diego State Aztecs An initiative by the sustainability Clint Eastwood’s “J. Edgar,” follows the met Tuesday in the team’s first NIT department aims to make organization life of an FBI secret-keeper, from his semifinals together since 2009 meetings more environmentally friendly career highs to personal lows Vol. 112 No. 43 © 2011, Baylor University In Print >> 3-D flop “Immortals,” from the Willie Nelson talks music legends same producers as “300,” is just as bloody but not Documentary highlights as big of a hit with some audiences. Tommy Duncan’s career page 4 By Mandy Power Tommy Duncan fan club, with the Contributor idea for the documentary. “I had recently started work- >> An end in sight Willie Nelson is a famous ing at Baylor and thought this The Lariat Super League is musician in his own right, but would be a great opportunity for still going strong, with five the country star says his career my students to have a real-world teams coming close to the wouldn’t be the same without the experience,” Callaway said. playoffs this week. influence of old friend and west- The documentary highlights ern swing legend Tommy Dun- Duncan’s career as the lead singer can. for the band Bob Wills and the Page 5 Three students and a Baylor Texas Playboys. -

Rosters Set for 2014-15 Nba Regular Season
ROSTERS SET FOR 2014-15 NBA REGULAR SEASON NEW YORK, Oct. 27, 2014 – Following are the opening day rosters for Kia NBA Tip-Off ‘14. The season begins Tuesday with three games: ATLANTA BOSTON BROOKLYN CHARLOTTE CHICAGO Pero Antic Brandon Bass Alan Anderson Bismack Biyombo Cameron Bairstow Kent Bazemore Avery Bradley Bojan Bogdanovic PJ Hairston Aaron Brooks DeMarre Carroll Jeff Green Kevin Garnett Gerald Henderson Mike Dunleavy Al Horford Kelly Olynyk Jorge Gutierrez Al Jefferson Pau Gasol John Jenkins Phil Pressey Jarrett Jack Michael Kidd-Gilchrist Taj Gibson Shelvin Mack Rajon Rondo Joe Johnson Jason Maxiell Kirk Hinrich Paul Millsap Marcus Smart Jerome Jordan Gary Neal Doug McDermott Mike Muscala Jared Sullinger Sergey Karasev Jannero Pargo Nikola Mirotic Adreian Payne Marcus Thornton Andrei Kirilenko Brian Roberts Nazr Mohammed Dennis Schroder Evan Turner Brook Lopez Lance Stephenson E'Twaun Moore Mike Scott Gerald Wallace Mason Plumlee Kemba Walker Joakim Noah Thabo Sefolosha James Young Mirza Teletovic Marvin Williams Derrick Rose Jeff Teague Tyler Zeller Deron Williams Cody Zeller Tony Snell INACTIVE LIST Elton Brand Vitor Faverani Markel Brown Jeffery Taylor Jimmy Butler Kyle Korver Dwight Powell Cory Jefferson Noah Vonleh CLEVELAND DALLAS DENVER DETROIT GOLDEN STATE Matthew Dellavedova Al-Farouq Aminu Arron Afflalo Joel Anthony Leandro Barbosa Joe Harris Tyson Chandler Darrell Arthur D.J. Augustin Harrison Barnes Brendan Haywood Jae Crowder Wilson Chandler Caron Butler Andrew Bogut Kentavious Caldwell- Kyrie Irving Monta Ellis -

What, Why and WHO Month
FOLLOW US: Monday, April 13, 2020 thehindu.in facebook.com/thehinduinschool twitter.com/the_hindu CONTACT US [email protected] Printed at . Chennai . Coimbatore . Bengaluru . Hyderabad . Madurai . Noida . Visakhapatnam . Thiruvananthapuram . Kochi . Vijayawada . Mangaluru . Tiruchirapalli . Kolkata . Hubballi . Mohali . Malappuram . Mumbai . Tirupati . lucknow . cuttack . patna No El Nino, La Nina this year? Both El Nino and La Nina can be destructive. REUTERS TOKYO: Japan's weather bureau said on Friday there was a 60% chance that there would be no El Nino or La Nina occurring from now through the northern hemisphere summer, repeating its forecast of last What, why and WHO month. Reuters HOTO: AP What’s El Nino? P What is the role of the World Health Organisation? Why is it embroiled in controversies after An El Nino phenomenon is a warming of ocean the outbreak of COVID-19? We get you the details... surface temperatures in the eastern and central Pacic that typically happens every few years, sometimes causing crop damage, ash oods or res. The World Health Taiwan, which has succeeded in Ethiopia’s former health and global health issues. This health regulations, improving In normal conditions, trade winds travel from east Organisation last week preventing a major outbreak, foreign minister Tedros organisation was established on access to medicines and medical to west across the tropical Pacic, pushing the warm appealed for global unity in warned the WHO on December Adhanom Ghebreyesus on April 7, 1948, and is devices, and preventing non surface waters near South America westward ghting the coronavirus. This 31 of humantohuman Wednesday spoke out for the headquartered in Geneva, communicable diseases among towards Indonesia. -

Cleveland Cavaliers (56-22) at Indiana Pacers (41-36)
WED., APRIL 6, 2016 BANKERS LIFE FIELDHOUSE – INDIANAPOLIS, IN TV: ESPN/FSO RADIO: 100.7 WMMS/LA MEGA 87.7 FM 7:00 PM EST CLEVELAND CAVALIERS (56-22) AT INDIANA PACERS (41-36) 2015-16 CLEVELAND CAVALIERS GAME NOTES OVERALL GAME # 79 ROAD GAME # 40 PROBABLE STARTERS 2015-16 SCHEDULE POS NO. PLAYER HT. WT. G GS PPG RPG APG FG% MPG 10/27 @ CHI Lost, 95-97 10/28 @ MEM WON, 106-76 F 23 LEBRON JAMES 6-8 250 15-16: 74 74 *25.0 7.5 >6.8 .514 35.6 10/30 vs. MIA WON, 102-92 11/2 @ PHI WON, 107-100 11/4 vs. NYK WON, 96-86 F 0 KEVIN LOVE 6-10 251 15-16: 74 74 16.0 ^9.9 2.4 .422 31.6 11/6 vs. PHI WON, 108-102 11/8 vs. IND WON, 101-97 11/10 vs. UTA WON, 118-114 C 20 TIMOFEY MOZGOV 7-1 275 15-16: 73 47 6.2 4.4 0.4 .565 17.3 11/13 @ NYK WON, 90-84 11/14 @ MIL Lost, 105-108** 11/17 @ DET Lost, 99-104 G 5 J.R. SMITH 6-6 225 15-16: 74 74 12.4 2.8 1.7 .414 30.7 11/19 vs. MIL WON, 115-100 11/21 vs. ATL WON, 109-97 G 2 KYRIE IRVING 6-3 193 15-16: 50 50 19.4 2.9 4.6 .446 31.2 11/23 vs. ORL WON, 117-103 11/25 @ TOR Lost, 99-103 11/27 @ CHA WON, 95-90 * Ranks 6th in NBA > Ranks 8th in NBA ^ Ranks 12th in NBA 11/28 vs. -

2011-12 Season in Review
Cavaliers Key Dates In The 2011-12 Season December 26 – The Cavaliers opened a shortened 66 game January 29 – In the first game of a home-and-home series with the 2011-12 season at Quicken Loans Arena against the Toronto Boston Celtics, the Cavaliers pulled off one of their most dramatic Raptors. Anderson Varejao recorded his first double-double of victories of the season. Trailing by 11 points with 4:25 left in the the season with 14 points and 10 rebounds, including seven fourth in Boston, the Cavs went on a 12-0 run to close out the offensive rebounds, in 33 minutes. Ramon Sessions led all game. Down one point in the final seconds, rookie Kyrie Irving scorers with 18 points in 22 minutes off the bench on 6-12 (.500) drove right, split two defenders and scored the game-winning shooting. Sessions also had six assists. The 2011 NBA Draft’s #1 layup with 2.6 seconds remaining. Irving finished with a overall pick Kyrie Irving and the 2011 NBA Draft’s #4 overall pick game-high 23 points and six assists, while Anderson Varejao put Tristan Thompson both made their NBA debuts. Irving finished up 18 points, to go along with nine rebounds. with six points, seven assists and only one turnover in 26 minutes. Thompson scored 12 points and pulled down five January 31 – In the second game of a home-and home series with rebounds in 17 minutes of action off the bench. Boston, Anderson Varejao had one of the finest games of his career, setting a season high in points and career highs in January 1 – Cleveland dominated the second half versus the New offensive rebounds and total rebounds with 20 points and 20 Jersey Nets which resulted in a 98-82 win at The Q on New rebounds, 10 of which were offensive. -

2008-09 Playoff Guide.Pdf
▪ TABLE OF CONTENTS ▪ Media Information 1 Staff Directory 2 2008-09 Roster 3 Mitch Kupchak, General Manager 4 Phil Jackson, Head Coach 5 Playoff Bracket 6 Final NBA Statistics 7-16 Season Series vs. Opponent 17-18 Lakers Overall Season Stats 19 Lakers game-By-Game Scores 20-22 Lakers Individual Highs 23-24 Lakers Breakdown 25 Pre All-Star Game Stats 26 Post All-Star Game Stats 27 Final Home Stats 28 Final Road Stats 29 October / November 30 December 31 January 32 February 33 March 34 April 35 Lakers Season High-Low / Injury Report 36-39 Day-By-Day 40-49 Player Biographies and Stats 51 Trevor Ariza 52-53 Shannon Brown 54-55 Kobe Bryant 56-57 Andrew Bynum 58-59 Jordan Farmar 60-61 Derek Fisher 62-63 Pau Gasol 64-65 DJ Mbenga 66-67 Adam Morrison 68-69 Lamar Odom 70-71 Josh Powell 72-73 Sun Yue 74-75 Sasha Vujacic 76-77 Luke Walton 78-79 Individual Player Game-By-Game 81-95 Playoff Opponents 97 Dallas Mavericks 98-103 Denver Nuggets 104-109 Houston Rockets 110-115 New Orleans Hornets 116-121 Portland Trail Blazers 122-127 San Antonio Spurs 128-133 Utah Jazz 134-139 Playoff Statistics 141 Lakers Year-By-Year Playoff Results 142 Lakes All-Time Individual / Team Playoff Stats 143-149 Lakers All-Time Playoff Scores 150-157 MEDIA INFORMATION ▪ ▪ PUBLIC RELATIONS CONTACTS PHONE LINES John Black A limited number of telephones will be available to the media throughout Vice President, Public Relations the playoffs, although we cannot guarantee a telephone for anyone. -

Ucla History
UUCLACLA HHISTORYISTORY RRETIREDETIRED JJERSEYERSEY NNUMBERSUMBERS #25 GAIL GOODRICH in scoring (18.2) and rebounding (8.8) to earn third-team All-American and fi rst-team All-Pac-10 for a second straight season … as a senior in Ceremony: On Dec. 18, 2004 in Pauley Pavilion, 1995, O’Bannon led UCLA to its 11th NCAA championship, he was named when UCLA hosted Michigan, Gail Goodrich, a the Most Outstanding Player at the Final Four, as he again paced UCLA in member of the Naismith Memorial Basketball Hall of scoring (20.4) and rebounding (8.3) … the Bruins won a school-record 32 Fame, had his No. 25 jersey retired, becoming the games, including a 19-game winning streak and O’Bannon was named seventh men’s basketball player in school history to National Player of the Year, by the John R. Wooden Award, USBWA and CBS- achieve this honor. Chevrolet, as well as Pac-10 co-Player of the Year … he was the ninth player Notes: A three-year letterman (1963-65) under taken in the ‘95 NBA draft by the New Jersey Nets … 2005 UCLA Athletics John Wooden, Goodrich was the leading scorer on Hall of Fame inductee. UCLA’s fi rst two (1964/1965) NCAA Championship teams … as a senior co-captain (with Keith Gail Goodrich Erickson) and All-American in 1965, he averaged #32 BILL WALTON a team-leading 24.8 points … in the 1965 NCAA Final, his then-championship game record 42 points led No. 2 UCLA to an Ceremony: On Feb. 3, 1990, four of the greatest 87-66 victory over No. -

2011-12 D-Fenders Media Guide Cover (FINAL).Psd
TABLE OF CONTENTS D-FENDERS STAFF D-FENDERS RECORDS & HISTORY Team Directory 4 Season-By-Season Record/Leaders 38 Owner/Governor Dr. Jerry Buss 5 Honor Roll 39 President/CEO Joey Buss 6 Individual Records (D-Fenders) 40 General Manager Glenn Carraro 6 Individual Records (Opponents) 41 Head Coach Eric Musselman 7 Team Records (D-Fenders) 42 Associate Head Coach Clay Moser 8 Team Records (Opponents) 43 Score Margins/Streaks/OT Record 44 Season-By-Season Statistics 45 THE PLAYERS All-Time Career Leaders 46 All-Time Roster with Statistics 47-52 Zach Andrews 10 All-Time Collegiate Roster 53 Jordan Brady 10 All-Time Numerical Roster 54 Anthony Coleman 11 All-Time Draft Choices 55 Brandon Costner 11 All-Time Player Transactions 56-57 Larry Cunningham 12 Year-by-Year Results, Statistics & Rosters 58-61 Robert Diggs 12 Courtney Fortson 13 Otis George 13 Anthony Gurley 14 D-FENDERS PLAYOFF RECORDS Brian Hamilton 14 Individual Records (D-Fenders) 64 Troy Payne 15 Individual Records (Opponents) 64 Eniel Polynice 15 D-Fenders Team Records 65 Terrence Roberts 16 Playoff Results 66-67 Brandon Rozzell 16 Franklin Session 17 Jamaal Tinsley 17 THE OPPONENTS 2011-12 Roster 18 Austin Toros 70 Bakersfield Jam 71 Canton Charge 72 THE D-LEAGUE Dakota Wizards 73 D-League Team Directory 20 Erie Bayhawks 74 NBA D-League Directory 21 Fort Wayne Mad Ants 75 D-League Overview 22 Idaho Stampede 76 Alignment/Affiliations 23 Iowa Energy 77 All-Time Gatorade Call-Ups 24-25 Maine Red Claws 78 All-Time NBA Assignments 26-27 Reno Bighorns 79 All-Time All D-League Teams 28 Rio Grande Valley Vipers 80 All-Time Award Winners 29 Sioux Falls Skyforce 81 D-League Champions 30 Springfield Armor 82 All-Time Single Game Records 31-32 Texas Legends 83 Tulsa 66ers 84 2010-11 YEAR IN REVIEW 2010-11 Standings/Playoff Results 34 MEDIA & GENERAL INFORMATION 2010-11 Team Statistics 35 Media Guidelines/General Information 86 2010-11 D-League Leaders 36 Toyota Sports Center 87 1 SCHEDULE 2011-12 D-FENDERS SCHEDULE DATE OPPONENT TIME DATE OPPONENT TIME Nov. -

Administration of Barack Obama, 2016 Remarks Honoring the 2016
Administration of Barack Obama, 2016 Remarks Honoring the 2016 National Basketball Association Champion Cleveland Cavaliers November 10, 2016 The President. Hello, everybody! Welcome to the White House, and give it up for the World Champion Cleveland Cavaliers! That's right, I said "World Champion" and "Cleveland" in the same sentence. [Laughter] That's what we're talking about when we talk about hope and change. [Laughter] We've got a lot of big Cavs fans here in the house, including Ohio's Governor, John Kasich, and his daughters Emma and Reese. We've got some outstanding Members of Congress that are here. And obviously we want to recognize Cavs owner Dan Gilbert, who put so much of himself into trying to make sure this thing worked. One of the great general managers of the game, David Griffin. And the pride and joy of Mexico, Missouri—[laughter]— Coach Tyronn Lue. I also, before I go any further, want to give a special thanks to J.R. Smith's shirt for showing up. [Laughter] I wasn't sure if it was going to make an appearance today. I'm glad you came. You're a very nice shirt. [Laughter] Now, last season, the Cavs were the favorites in the East all along, but the road was anything but stable. And I'm not even talking about what happened on the court. There were rumors about who was getting along with who, and why somebody wasn't in a picture, and LeBron is tweeting—[laughter]—and this was all big news. But somehow Coach Lue comes in and everything starts getting a little smoother, and they hit their stride in the playoffs. -
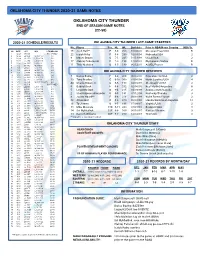
Thunder 2020-21 Game Notes
OKLAHOMA CITY THUNDER 2020-21 GAME NOTES OKLAHOMA CITY THUNDER END OF SEASON GAME NOTES (22-50) 2020-21 SCHEDULE/RESULTS OKLAHOMA CITY THUNDER LAST GAME STARTERS No. Player Pos. Ht. Wt. Birthdate Prior to NBA/Home Country NBA Yr. NO DATE OPP W/L **TV/RECORD 15 Josh Hall** F 6-8 200 10/08/00 Moravian Prep/USA R 1 12/23 @ HOU POSTPONED 22 Isaiah Roby F 6-8 230 02/03/98 Nebraska/USA 2 2 12/26 @ CHA W, 109-107 1-0 9 Moses Brown C 7-1 245 10/13/99 UCLA/USA 2 3 12/28 vs. UTA L, 109-110 1-1 4 12/29 vs. ORL L, 107-118 1-2 17 Aleksej Pokuševski F 7-0 195 12/26/01 Olympiacos/Serbia R 5 12/31 vs. NOP L, 80-113 1-3 6 1/2 @ ORL W, 108-99 2-3 11 Théo Maledon G 6-5 180 06/12/01 ASVEL/France R 7 1/4 @ MIA L, 90-118 2-4 8 1/6 @ NOP W, 111-110 3-4 OKLAHOMA CITY THUNDER RESERVES 9 1/8 @ NYK W, 101-89 4-4 10 1/10 @ BKN W, 129-116 5-4 11 1/12 vs. SAS L, 102-112 5-5 7 Darius Bazley F 6-8 208 06/12/00 Princeton HS/USA 2 12 1/13 vs. LAL L, 99-128 5-6 13 Tony Bradley C 6-10 260 01/08/98 North Carolina/USA 4 13 1/15 vs. CHI W, 127-125 (OT) 6-6 44 Charlie Brown Jr.