New Notation in Series of Functions
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

The Five Fundamental Operations of Mathematics: Addition, Subtraction
The five fundamental operations of mathematics: addition, subtraction, multiplication, division, and modular forms Kenneth A. Ribet UC Berkeley Trinity University March 31, 2008 Kenneth A. Ribet Five fundamental operations This talk is about counting, and it’s about solving equations. Counting is a very familiar activity in mathematics. Many universities teach sophomore-level courses on discrete mathematics that turn out to be mostly about counting. For example, we ask our students to find the number of different ways of constituting a bag of a dozen lollipops if there are 5 different flavors. (The answer is 1820, I think.) Kenneth A. Ribet Five fundamental operations Solving equations is even more of a flagship activity for mathematicians. At a mathematics conference at Sundance, Robert Redford told a group of my colleagues “I hope you solve all your equations”! The kind of equations that I like to solve are Diophantine equations. Diophantus of Alexandria (third century AD) was Robert Redford’s kind of mathematician. This “father of algebra” focused on the solution to algebraic equations, especially in contexts where the solutions are constrained to be whole numbers or fractions. Kenneth A. Ribet Five fundamental operations Here’s a typical example. Consider the equation y 2 = x3 + 1. In an algebra or high school class, we might graph this equation in the plane; there’s little challenge. But what if we ask for solutions in integers (i.e., whole numbers)? It is relatively easy to discover the solutions (0; ±1), (−1; 0) and (2; ±3), and Diophantus might have asked if there are any more. -

Subtraction Strategy
Subtraction Strategies Bley, N.S., & Thornton, C.A. (1989). Teaching mathematics to the learning disabled. Austin, TX: PRO-ED. These math strategies focus on subtraction. They were developed to assist students who are experiencing difficulty remembering subtraction facts, particularly those facts with teen minuends. They are beneficial to students who put heavy reliance on counting. Students can benefit from of the following strategies only if they have ability: to recognize when two or three numbers have been said; to count on (from any number, 4 to 9); to count back (from any number, 4 to 12). Students have to make themselves master related addition facts before using subtraction strategies. These strategies are not research based. Basic Sequence Count back 27 Count Backs: (10, 9, 8, 7, 6, 5, 4, 3, 2) - 1 (11, 10, 9, 8, 7, 6, 5, 4, 3) - 2 (12, 11, 10, 9, 8, 7, 6, 5,4) – 3 Example: 12-3 Students start with a train of 12 cubes • break off 3 cubes, then • count back one by one The teacher gets students to point where they touch • look at the greater number (12 in 12-3) • count back mentally • use the cube train to check Language emphasis: See –1 (take away 1), -2, -3? Start big and count back. Add to check After students can use a strategy accurately and efficiently to solve a group of unknown subtraction facts, they are provided with “add to check activities.” Add to check activities are additional activities to check for mastery. Example: Break a stick • Making "A" train of cubes • Breaking off "B" • Writing or telling the subtraction sentence A – B = C • Adding to check Putting the parts back together • A - B = C because B + C = A • Repeating Show with objects Introduce subtraction zero facts Students can use objects to illustrate number sentences involving zero 19 Zeros: n – 0 = n n – n =0 (n = any number, 0 to 9) Use a picture to help Familiar pictures from addition that can be used to help students with subtraction doubles 6 New Doubles: 8 - 4 10 - 5 12 - 6 14 - 7 16 - 8 18-9 Example 12 eggs, remove 6: 6 are left. -

Number Sense and Numeration, Grades 4 to 6
11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page i Number Sense and Numeration, Grades 4 to 6 Volume 2 Addition and Subtraction A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6 2006 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 2 Every effort has been made in this publication to identify mathematics resources and tools (e.g., manipulatives) in generic terms. In cases where a particular product is used by teachers in schools across Ontario, that product is identified by its trade name, in the interests of clarity. Reference to particular products in no way implies an endorsement of those products by the Ministry of Education. 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 1 Number Sense and Numeration, Grades 4 to 6 Volume 2 Addition and Subtraction A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 4 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 3 CONTENTS Introduction 5 Relating Mathematics Topics to the Big Ideas............................................................................. 6 The Mathematical Processes............................................................................................................. 6 Addressing the Needs of Junior Learners ..................................................................................... 8 Learning About Addition and Subtraction in the Junior Grades 11 Introduction......................................................................................................................................... -

Solving for the Unknown: Logarithms and Quadratics ID1050– Quantitative & Qualitative Reasoning Logarithms
Solving for the Unknown: Logarithms and Quadratics ID1050– Quantitative & Qualitative Reasoning Logarithms Logarithm functions (common log, natural log, and their (evaluating) inverses) represent exponents, so they are the ‘E’ in PEMDAS. PEMDAS (inverting) Recall that the common log has a base of 10 • Parentheses • Log(x) = y means 10y=x (10y is also known as the common anti-log) Exponents Multiplication • Recall that the natural log has a base of e Division y y Addition • Ln(x) = y means e =x (e is also know as the natural anti-log) Subtraction Function/Inverse Pairs Log() and 10x LN() and ex Common Logarithm and Basic Operations • 2-step inversion example: 2*log(x)=8 (evaluating) PEMDAS • Operations on x: Common log and multiplication by 2 (inverting) • Divide both sides by 2: 2*log(x)/2 = 8/2 or log(x) = 4 Parentheses • Take common anti-log of both sides: 10log(x) = 104 or x=10000 Exponents Multiplication • 3-step inversion example: 2·log(x)-5=-4 Division Addition • Operations on x: multiplication, common log, and subtraction Subtraction • Add 5 to both sides: 2·log(x)-5+5=-4+5 or 2·log(x)=1 Function/Inverse Pairs 2·log(x)/2=1/2 log(x)=0.5 • Divide both sides by 2: or Log() and 10x • Take common anti-log of both sides: 10log(x) = 100.5 or x=3.16 LN() and ex Common Anti-Logarithm and Basic Operations • 2-step inversion example: 5*10x=6 (evaluating) PEMDAS x • Operations on x: 10 and multiplication (inverting) • Divide both sides by 5: 5*10x/5 = 6/5 or 10x=1.2 Parentheses • Take common log of both sides: log(10x)=log(1.2) or x=0.0792 -

Operation CLUE WORDS Remember, Read Each Question Carefully
Operation CLUE WORDS Remember, read each question carefully. THINK about what the question is asking. Addition Subtraction add difference altogether fewer and gave away both take away in all how many more sum how much longer/ total shorter/smaller increase left less change Multiplication decrease each same twice Division product share equally in all (each) each double quotient every ©2012 Amber Polk-Adventures of a Third Grade Teacher Clue Word Cut and Paste Cut out the clue words. Sort and glue under the operation heading. Subtraction Multiplication Addition Division add each difference share equally both fewer in all twice product every gave away change quotient sum total left double less decrease increase ©2012 Amber Polk-Adventures of a Third Grade Teacher Clue Word Problems Underline the clue word in each word problem. Write the equation. Solve the problem. 1. Mark has 17 gum balls. He 5. Sara and her two friends bake gives 6 gumballs to Amber. a pan of 12 brownies. If the girls How many gumballs does Mark share the brownies equally, how have left? many will each girl have? 2. Lauren scored 6 points during 6. Erica ate 12 grapes. Riley ate the soccer game. Diana scored 3 more grapes than Erica. How twice as many points. How many grapes did both girls eat? many points did Diana score? 3. Kyle has 12 baseball cards. 7. Alice the cat is 12 inches long. Jason has 9 baseball cards. Turner the dog is 19 inches long. How many do they have How much longer is Turner? altogether? 4. -

1 Modular Arithmetic
1 Modular Arithmetic Definition 1.1 (A divides B). Let A; B 2 Z. We say that A divides B (or A is a divisor of B), denoted AjB, if there is a number C 2 Z such that B = AC. Definition 1.2 (Prime number). Let P 2 N. We say that P is a prime number if P ≥ 2 and the only divisors of P are 1 and P . Definition 1.3 (Congruence modulo N). We denote by A mod N the remainder you get when you divide A by N. Note that A mod N 2 f0; 1; 2; ··· ;N − 1g. We say that A and B are congruent modulo N, denoted A ≡N B (or A ≡ B mod N), if A mod N = B mod N. Exercise 1.4. Show that A ≡N B if and only if Nj(A − B). Remark. The above characterization of A ≡N B can be taken as the definition of A ≡N B. Indeed, it is used a lot in proofs. Notation 1.5. We write gcd(A; B) to denote the greatest common divisor of A and B. Note that for any A, gcd(A; 1) = 1 and gcd(A; 0) = A. Definition 1.6 (Relatively prime). We say that A and B are relatively prime if gcd(A; B) = 1. Below, in Section 1.1, we first give the definitions of basic modular operations like addition, subtraction, multiplication, division and exponentiation. We also explore some of their properties. Later, in Section 1.2, we look at the computational complexity of these operations. -

Subtraction by Addition
Memory & Cognition 2008, 36 (6), 1094-1102 doi: 10.3758/MC.36.6.1094 Subtraction by addition JAMIE I. D. CAMPBELL University of Saskatchewan, Saskatoon, Saskatchewan, Canada University students’ self-reports indicate that they often solve basic subtraction problems (13 6 ?) by reference to the corresponding addition problem (6 7 13; therefore, 13 6 7). In this case, solution latency should be faster with subtraction problems presented in addition format (6 _ 13) than in standard subtraction format (13 6 _). In Experiment 1, the addition format resembled the standard layout for addition with the sum on the right (6 _ 13), whereas in Experiment 2, the addition format resembled subtraction with the minuend on the left (13 6 _). Both experiments demonstrated a latency advantage for large problems (minuend 10) in the addition format as compared with the subtraction format (13 6 _), although the effect was larger in Experiment 1 (254 msec) than in Experiment 2 (125 msec). Small subtractions (minuend 10) in Experiment 1 were solved equally quickly in the subtraction or addition format, but in Experiment 2, performance on small problems was faster in the standard format (5 3 _) than in the addition format (5 3 _). The results indicate that educated adults often use addition reference to solve large simple subtraction problems, but that theyyy rely on direct memory retrieval for small subtractions. The cognitive processes that subserve performance of ementary arithmetic, small problems are often defined as elementary calculation (e.g., 2 6 8; 6 7 42) those with either a sum/minuend 10 (Seyler, Kirk, & have received extensive experimental analysis over the Ashcraft, 2003) or a product/dividend 25 (Campbell & last quarter century. -

PEMDAS Review If We're Asked to Do Something Like 3 + 4 · 2, The
PEMDAS Review If we’re asked to do something like 3 + 4 · 2, the question of “How do I go about doing this” would probably arise since there are two operations. We can do this in two ways: Choice Operation Description First 3+4 · 2=7 · 2=14 Add 3 and 4 and then multiply by 2 Second 3+4 · 2=3+8=11 Multiply 4 and 2 together and then add 3 It seems as though the answer depends on which how you look at the problem. But we can’t have this kind of flexibility in mathematics. It won’t work if you can’t be sure of a process to find a solution, or if the exact same problem can calculate to two or more differing solutions. To eliminate this confusion, we have some rules set up to follow. These were established at least as far back as the 1500s and are called the “order of operations.” The “operations” are addition, subtraction, multiplication, division, exponentiation, and grouping. The “order” of these operations states which operations take precedence over other operations. We follow the following logical acronym when performing any arithmetic: PEMD−−→−→AS Step Operations Description Perform... 1 P Parenthesis all operations in parenthesis 2 E Exponentiation any exponents 3 −−→MD Multiplication and Division multiplication and division from left to right 3 −→AS Addition and Subtraction addition and subtraction from left to right Note 1. Multiplication and division can be in any order; that is, you perform multiplication or division from the left and find the next multiplication or division and so forth. -

Basic Math Quick Reference Ebook
This file is distributed FREE OF CHARGE by the publisher Quick Reference Handbooks and the author. Quick Reference eBOOK Click on The math facts listed in this eBook are explained with Contents or Examples, Notes, Tips, & Illustrations Index in the in the left Basic Math Quick Reference Handbook. panel ISBN: 978-0-615-27390-7 to locate a topic. Peter J. Mitas Quick Reference Handbooks Facts from the Basic Math Quick Reference Handbook Contents Click a CHAPTER TITLE to jump to a page in the Contents: Whole Numbers Probability and Statistics Fractions Geometry and Measurement Decimal Numbers Positive and Negative Numbers Universal Number Concepts Algebra Ratios, Proportions, and Percents … then click a LINE IN THE CONTENTS to jump to a topic. Whole Numbers 7 Natural Numbers and Whole Numbers ............................ 7 Digits and Numerals ........................................................ 7 Place Value Notation ....................................................... 7 Rounding a Whole Number ............................................. 8 Operations and Operators ............................................... 8 Adding Whole Numbers................................................... 9 Subtracting Whole Numbers .......................................... 10 Multiplying Whole Numbers ........................................... 11 Dividing Whole Numbers ............................................... 12 Divisibility Rules ............................................................ 13 Multiples of a Whole Number ....................................... -
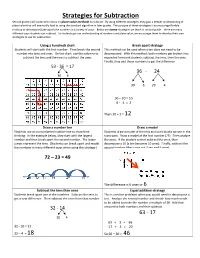
Strategies for Subtraction Second Graders Will Continue to Focus on Place Value Methods to Subtract
Strategies for Subtraction Second graders will continue to focus on place value methods to subtract. By using different strategies, they gain a deeper understanding of place value that will eventually lead to using the standard algorithm in later grades. The purpose of these strategies is to encourage flexible thinking to decompose (take apart) the numbers in a variety of ways. Below are some strategies we teach in second grade – there are many different ways students can subtract. As students gain an understanding of numbers and place value, we encourage them to develop their own strategies to use for subtraction. Using a hundreds chart Break apart strategy Students will start with the first number. Then break the second This method can be used when a ten does not need to be number into tens and ones. On the chart, use the columns to decomposed. With this method, both numbers get broken into subtract the tens and the rows to subtract the ones. expanded form and students subtract the tens, then the ones. Finally, they add those numbers to get the difference. 53 - 36 = 17 36 - 24 30 6 30 6 20 4 30 – 20 = 10 6 - 4 = 2 Then 10 + 2 = 12 Draw a number line Draw a model Students use an un-numbered number line to show their Students draw a model of the tens and ones blocks we use in the thinking. In the example below, they start with the largest classroom. Draw a model of the first number (21). Then analyze number and then break apart the second number. -

Arithmetic Operations- Addition and Subtraction
Chapter 03: Computer Arithmetic Lesson 02: Arithmetic Operations─ Addition and subtraction Schaum’s Outline of Theory and Problems of Computer Architecture 1 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Objective • Understand sign extension of 2’s complement number • Negation • Addition • Subtraction Schaum’s Outline of Theory and Problems of Computer Architecture 2 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Sign Extension Schaum’s Outline of Theory and Problems of Computer Architecture 3 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Sign Extension • Used in order to equalize the number of bits in two operands for addition and subtraction • Sign extension of 8-bit integer in 2’s complement number representation becomes 16- bit number 2’s complement number representation by sign extension Schaum’s Outline of Theory and Problems of Computer Architecture 4 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Sign Extension • When m-bit number sign extends to get n-bit number then bm-1 copies into extended places upto bn-1. • msb (b7) in an 8 bit number copies into b15, b14, b13, b12, b11, b10, b9 and b8 to get 16-bit sign extended number in 2’s complement representation Schaum’s Outline of Theory and Problems of Computer Architecture 5 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Examples • 01000011b becomes 000000000100 0011b • 1100 0011b becomes 111111111100 0011b Schaum’s Outline of Theory and Problems of Computer Architecture 6 Copyright © The McGraw-Hill Companies Inc. Indian Special Edition 2009 Negation Schaum’s Outline of Theory and Problems of Computer Architecture 7 Copyright © The McGraw-Hill Companies Inc. -

Analysis of the Relationship Between the Nth Root Which Is a Whole Number and the N Consecutive Odd Numbers
http://jct.sciedupress.com Journal of Curriculum and Teaching Vol. 4, No. 2; 2015 Analysis of the Relationship between the nth Root which is a Whole Number and the n Consecutive Odd Numbers Kwenge Erasmus1,*, Mwewa Peter2 & Mulenga H.M3 1Mpika Day Secondary School, P.O. Box 450004, Mpika, Zambia 2Department of Mathematics and Statistics, Mukuba University, P.O. Box 20382, Itimpi, Kitwe, Zambia 3Department of Mathematics, Copperbelt University, P.O. Box 21692, Kitwe, Zambia *Correspondence: Mpika Day Secondary School, P.O. Box 450004, Mpika, Zambia. Tel: 260-976-379-410. E-mail: [email protected] Received: April 22, 2015 Accepted: July 12, 2015 Online Published: August 7, 2015 doi:10.5430/jct.v4n2p35 URL: http://dx.doi.org/10.5430/jct.v4n2p35 Abstract The study was undertaken to establish the relationship between the roots of the perfect numbers and the n consecutive odd numbers. Odd numbers were arranged in such a way that their sums were either equal to the perfect square number or equal to a cube. The findings on the patterns and relationships of the numbers showed that there was a relationship between the roots of numbers and n consecutive odd numbers. From these relationships a general formula was derived which can be used to determine the number of consecutive odd numbers that can add up to get the given number and this relationship was used to define the other meaning of nth root of a given perfect number from consecutive n odd numbers point of view. If the square root of 4 is 2, then it means that there are 2 consecutive odd numbers that can add up to 4, if the cube root of 27 is 3, then there are 3 consecutive odd number that add up to 27, if the fifth root of 32 is 5, then it means that there are 5 consecutive odd numbers that add up to 32.