DOCSLIB.ORG

Mnemonic Strategies to Teach Addition, Subtraction, Multiplication and Division Facts and Math Vocabulary

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mnemonic Strategies to Teach Addition, Subtraction, Multiplication and Division Facts and Math Vocabulary Mnemonic Strategies to Teach Addition, Subtraction, Multiplication and Division Facts and Math Vocabulary Presenter: Donnalyn Yates, M.Ed. Learning Styles Visual Learners – (65%) Seeing pictures, diagrams, and charts enhances memorization skills. Auditory Learners – (30%) Learn best by lectures, discussions, need to repeat things aloud. Kinesthetic Learners – (5%) Active participation, using manipulatives, drama to learn. Understanding How Memory Works The brain has three types of memory. 1. Sensory Memory 2. Short Term (or working memory) 3. Long Term Memory Moving Information From Short Term to Long Term Memory 1. Meaningfulness & Familiarity - It has to make sense & be familiar. 2. Rhymes - Songs and rhymes imprint the instructional message 90% faster than any other strategy! 3. Patterns - Finding a pattern, rule or underlying principle in the material, enhances memory. 4. Associations - Using association methods is one of the best retention mechanisms that we can employ in learning. It is also a method that is not used to it’s maximum potential. 5. Visualization - Studies on visualization prove that images are much more memorable than words. 6. Repetition - 5/5 Rule. Repeat the fact 5 times a day for 5 days. 7. Fun!!! - If an activity is fun, it is much more likely that it will be remembered. 8. Motivation - Student needs to make a verbal commitment to memorize information. Rhymes to Help Remember Math The Shape Song Days of the Week (Tune: Farmer in the Dell) Sunday learn the Golden Rule Monday off we go to school A circle’s like a ball, Tuesday is a day to add A circle’s like a ball, Wednesday we are kind of bad Round and round, it never stops, Thursday teacher gives a test A circle’s like a ball. Friday we will do our best Saturday is here for play A square is like a box, Now you know the 7 days. A square is like a box, It has 4 sides, they are the same, Sum A square is like a box. “Sum” apples are green. “Sum” apples are red. “Sum” is the answer when you add in your head A triangle has 3 sides, A triangle has 3 sides, Regrouping Up the mountain, down and back, “Bigger Bottom, Better Borrow” A triangle has 3 sides. In all A rectangle has 4 sides, How many balls in all? A rectangle has 4 sides, We add to get the call. 2 are long and 2 are short, A rectangle has 4 sides. Difference Difference, difference A pentagon has 5 sides, What can it be? A pentagon has 5 sides, The subtraction answer Draw a square with an extra side, Don’t you see? A pentagon has 5 sides. Isosceles Triangle Visual learners need to draw the Oh isosceles, oh isosceles shapes and see them as they sing. Two angles have equal degrees. Kinesthetic learners like to make the Oh isosceles, oh isosceles, shapes with their hands. You look just like a Christmas tree. Song for Even (Sing to BINGO) Song for Odd (Sing to BINGO) There was a farmer, who had a pig, There was a farmer, who had a cow, And EVEN was his name-O And ODD was his name-O 2, 4, 6, 8, 10 1, 3, 5, 7, 9 2, 4, 6, 8, 10 1, 3, 5, 7, 9 2, 4, 6, 8, 10 1, 3, 5, 7, 9 And EVEN was his name-O. And ODD was his name-O. Coin Rhyme Months in Order Penny, penny, January, February, Easily spent, March and April too, Copper brown The first four months And worth one cent. Bring happiness to you. Nickel, nickel, May and June, Thick and fat, July and August You’re worth five cents, Lots of fun I know that. When summer’s hottest. Dime, dime September, October, Little and thin, The leaves are falling. I remember, November, December, You’re worth ten. Holidays are calling. Quarter, quarter, These 12 months Big and bold, Are easy to remember, Worth twenty-five 52 weeks from I am told. Jan. to December. Patterns for Memorization The brain records information in images and patterns. It’s like a filing cabinet with intricate organization skills. Repeating patterns are easy to store and recall. Counting by Five: Use a “sing-song” voice and clap to the syllables. Five, ten (2) slow claps Fifteen, twenty (4) even claps Twenty-five, thirty (3) fast, (2 even claps) Thirty-five, forty (3) fast, (2 even claps) Forty-five, fifty (3) fast, (2 even claps) Fifty-five, sixty (3) fast, (2 even claps) Sixty-five, seventy (3) fast, (2 even claps) Seventy-five, eighty (3) fast, (2 even claps) Eighty-five, ninety (3) fast, (2 even claps) Ninety-five, one hundred! (3) fast, (3 even claps) Associations Make Connections in the Brain Acronyms – a silly saying using the first letter of the word or list to be memorized. Remembering the sequencing of the metric system: My Cat Drank Milky Ketchup The M in My is for millimeter. The C in Cat is for centimeter The D in Drank is for decimeter The M in Milky is for meter The K in Ketchup is for kilometer Roman Numerals in Order: I Value Xylophones Like Cows Drink Milk I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 Remembering the Procedural Order of Operations in Algebra Please Excuse My Dear Aunt Sally Parentheses Exponents Multiply Divide Add Subtract Remembering the Procedural Order of Operations of Long Division Dad = Divide Mother = Multiply Sister = Subtract Brother = Bring Down Rover (the dog) = Remainder Stories – Stories are easier to remember than random information. Good books to use for remembering measurement are the Scholastic Series, Sir Cumference. There are about 10 different books for math in this series. King Inch in the Kingdom of Measure (Located in the back of the hand-out) Read the story aloud and discuss the different measurement tools mentioned. Students can draw pictures illustrating the parts of the story and make a book from their pages. Stories suggest visual pictures and help students remember the measurement terms. Visualization A picture is worth a thousand words. Visual learners memorize and store information with images. To remember the term and meaning for rhombus, draw a parallelogram with all sides congruent and push it over. It becomes a rhom bus. Draw a picture and make an association between the word and the meaning. How to Remember Liquid Measurement (Using a visual and story) The Kingdom of Gallon Once upon a time, long, long ago, there was a kingdom called The Kingdom of Gallon. (Students draw a big G on their paper, filling the entire page. Explain the G represents Gallon) In the Kingdom of Gallon there lived four Queens. They were sisters and all looked exactly alike. (Draw 4 big Q’s and explain the Q also represents Quart.) I hate to tell you this, but soon the four queens got into a huge fight and couldn’t agree on how to rule over the Kingdom of Gallon. Finally they decided to split the kingdom in half. Two queens ruled a Half Gallon in the north, and the other two queens ruled the Half Gallon Kingdom in the south. (Look for the dividing line on the G for each kingdom.) Now that there was peace in the kingdoms, the queens got married and each one had a Prince and a Princess. (With what letter does Prince and Princess begin? The P stands for Pint. Draw two letter P’s inside each Q.) There is something I forgot to tell you. Each Prince had two cats and each Princess had two cats. (The C for cats reminds us of C for Cups. Draw two C’s inside each P. Ask random questions about how many quarts in a gallon, how many pints in a quart etc. to make sure students are able to visualize the picture to find the answer.) Rounding Numbers Visually Draw a long line of hills on the whiteboard. If you are rounding to the nearest 10, begin at the left and write 0 on the bottom of the first hill, making number designations up to 5 at the top of the hill. Continue with each hill. All of the ten endings should be in the valley and the 5 endings on top of each hill. Obtain a picture of a car and attach a magnet to the back. Place the car at number 14 and talk about getting out to look at the view and forgetting set the brake. Which way would the car roll? (Down to the 10.) Place the car at the top of the hill. Which way would the car roll? Since the engine is in the front and is heavier, it would roll down the hill to number 20. (Have students try putting it at different locations to see which number it would round to. Visual learners benefit from this picture of rounding. Now it makes sense to them.) More Visual Math Vocabulary h o r i z o n t a l p a r a l l e l radius short d i a m e t e r long Remember this, and you’ll never get it wrong! Repetition and Fun If an activity is fun it becomes easy to repeat. Repetition helps place information in long-term memory but it needs to be fun or students will tune out. Try this activity for fun! Counting by TEN Ten, twenty Touch each foot Thirty, forty Touch each knee Fifty, sixty Touch each hip Seventy, eighty Touch each shoulder Ninety, one-hundred Touch each ear and put hands in air Memorizing Addition and Subtraction Facts What is the Memory Joggers method? 1.
Load more

Recommended publications
  • The Five Fundamental Operations of Mathematics: Addition, Subtraction
    The five fundamental operations of mathematics: addition, subtraction, multiplication, division, and modular forms Kenneth A. Ribet UC Berkeley Trinity University March 31, 2008 Kenneth A. Ribet Five fundamental operations This talk is about counting, and it’s about solving equations. Counting is a very familiar activity in mathematics. Many universities teach sophomore-level courses on discrete mathematics that turn out to be mostly about counting. For example, we ask our students to find the number of different ways of constituting a bag of a dozen lollipops if there are 5 different flavors. (The answer is 1820, I think.) Kenneth A. Ribet Five fundamental operations Solving equations is even more of a flagship activity for mathematicians. At a mathematics conference at Sundance, Robert Redford told a group of my colleagues “I hope you solve all your equations”! The kind of equations that I like to solve are Diophantine equations. Diophantus of Alexandria (third century AD) was Robert Redford’s kind of mathematician. This “father of algebra” focused on the solution to algebraic equations, especially in contexts where the solutions are constrained to be whole numbers or fractions. Kenneth A. Ribet Five fundamental operations Here’s a typical example. Consider the equation y 2 = x3 + 1. In an algebra or high school class, we might graph this equation in the plane; there’s little challenge. But what if we ask for solutions in integers (i.e., whole numbers)? It is relatively easy to discover the solutions (0; ±1), (−1; 0) and (2; ±3), and Diophantus might have asked if there are any more.
    [Show full text]
  • Lesson 2: the Multiplication of Polynomials
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M1 ALGEBRA II Lesson 2: The Multiplication of Polynomials Student Outcomes . Students develop the distributive property for application to polynomial multiplication. Students connect multiplication of polynomials with multiplication of multi-digit integers. Lesson Notes This lesson begins to address standards A-SSE.A.2 and A-APR.C.4 directly and provides opportunities for students to practice MP.7 and MP.8. The work is scaffolded to allow students to discern patterns in repeated calculations, leading to some general polynomial identities that are explored further in the remaining lessons of this module. As in the last lesson, if students struggle with this lesson, they may need to review concepts covered in previous grades, such as: The connection between area properties and the distributive property: Grade 7, Module 6, Lesson 21. Introduction to the table method of multiplying polynomials: Algebra I, Module 1, Lesson 9. Multiplying polynomials (in the context of quadratics): Algebra I, Module 4, Lessons 1 and 2. Since division is the inverse operation of multiplication, it is important to make sure that your students understand how to multiply polynomials before moving on to division of polynomials in Lesson 3 of this module. In Lesson 3, division is explored using the reverse tabular method, so it is important for students to work through the table diagrams in this lesson to prepare them for the upcoming work. There continues to be a sharp distinction in this curriculum between justification and proof, such as justifying the identity (푎 + 푏)2 = 푎2 + 2푎푏 + 푏 using area properties and proving the identity using the distributive property.
    [Show full text]
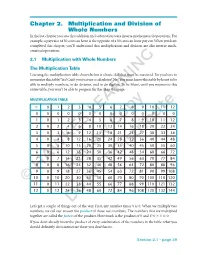
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Grade 7/8 Math Circles the Scale of Numbers Introduction
    Faculty of Mathematics Centre for Education in Waterloo, Ontario N2L 3G1 Mathematics and Computing Grade 7/8 Math Circles November 21/22/23, 2017 The Scale of Numbers Introduction Last week we quickly took a look at scientific notation, which is one way we can write down really big numbers. We can also use scientific notation to write very small numbers. 1 × 103 = 1; 000 1 × 102 = 100 1 × 101 = 10 1 × 100 = 1 1 × 10−1 = 0:1 1 × 10−2 = 0:01 1 × 10−3 = 0:001 As you can see above, every time the value of the exponent decreases, the number gets smaller by a factor of 10. This pattern continues even into negative exponent values! Another way of picturing negative exponents is as a division by a positive exponent. 1 10−6 = = 0:000001 106 In this lesson we will be looking at some famous, interesting, or important small numbers, and begin slowly working our way up to the biggest numbers ever used in mathematics! Obviously we can come up with any arbitrary number that is either extremely small or extremely large, but the purpose of this lesson is to only look at numbers with some kind of mathematical or scientific significance. 1 Extremely Small Numbers 1. Zero • Zero or `0' is the number that represents nothingness. It is the number with the smallest magnitude. • Zero only began being used as a number around the year 500. Before this, ancient mathematicians struggled with the concept of `nothing' being `something'. 2. Planck's Constant This is the smallest number that we will be looking at today other than zero.
    [Show full text]
  • Subtraction Strategy
    Subtraction Strategies Bley, N.S., & Thornton, C.A. (1989). Teaching mathematics to the learning disabled. Austin, TX: PRO-ED. These math strategies focus on subtraction. They were developed to assist students who are experiencing difficulty remembering subtraction facts, particularly those facts with teen minuends. They are beneficial to students who put heavy reliance on counting. Students can benefit from of the following strategies only if they have ability: to recognize when two or three numbers have been said; to count on (from any number, 4 to 9); to count back (from any number, 4 to 12). Students have to make themselves master related addition facts before using subtraction strategies. These strategies are not research based. Basic Sequence Count back 27 Count Backs: (10, 9, 8, 7, 6, 5, 4, 3, 2) - 1 (11, 10, 9, 8, 7, 6, 5, 4, 3) - 2 (12, 11, 10, 9, 8, 7, 6, 5,4) – 3 Example: 12-3 Students start with a train of 12 cubes • break off 3 cubes, then • count back one by one The teacher gets students to point where they touch • look at the greater number (12 in 12-3) • count back mentally • use the cube train to check Language emphasis: See –1 (take away 1), -2, -3? Start big and count back. Add to check After students can use a strategy accurately and efficiently to solve a group of unknown subtraction facts, they are provided with “add to check activities.” Add to check activities are additional activities to check for mastery. Example: Break a stick • Making "A" train of cubes • Breaking off "B" • Writing or telling the subtraction sentence A – B = C • Adding to check Putting the parts back together • A - B = C because B + C = A • Repeating Show with objects Introduce subtraction zero facts Students can use objects to illustrate number sentences involving zero 19 Zeros: n – 0 = n n – n =0 (n = any number, 0 to 9) Use a picture to help Familiar pictures from addition that can be used to help students with subtraction doubles 6 New Doubles: 8 - 4 10 - 5 12 - 6 14 - 7 16 - 8 18-9 Example 12 eggs, remove 6: 6 are left.
    [Show full text]
  • Number Sense and Numeration, Grades 4 to 6
    11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page i Number Sense and Numeration, Grades 4 to 6 Volume 2 Addition and Subtraction A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6 2006 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 2 Every effort has been made in this publication to identify mathematics resources and tools (e.g., manipulatives) in generic terms. In cases where a particular product is used by teachers in schools across Ontario, that product is identified by its trade name, in the interests of clarity. Reference to particular products in no way implies an endorsement of those products by the Ministry of Education. 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 1 Number Sense and Numeration, Grades 4 to 6 Volume 2 Addition and Subtraction A Guide to Effective Instruction in Mathematics, Kindergarten to Grade 6 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 4 11047_nsn_vol2_add_sub_05.qxd 2/2/07 1:33 PM Page 3 CONTENTS Introduction 5 Relating Mathematics Topics to the Big Ideas............................................................................. 6 The Mathematical Processes............................................................................................................. 6 Addressing the Needs of Junior Learners ..................................................................................... 8 Learning About Addition and Subtraction in the Junior Grades 11 Introduction.........................................................................................................................................
    [Show full text]
  • The Notion Of" Unimaginable Numbers" in Computational Number Theory
    Beyond Knuth’s notation for “Unimaginable Numbers” within computational number theory Antonino Leonardis1 - Gianfranco d’Atri2 - Fabio Caldarola3 1 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] 2 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy 3 Department of Mathematics and Computer Science, University of Calabria Arcavacata di Rende, Italy e-mail: [email protected] Abstract Literature considers under the name unimaginable numbers any positive in- teger going beyond any physical application, with this being more of a vague description of what we are talking about rather than an actual mathemati- cal definition (it is indeed used in many sources without a proper definition). This simply means that research in this topic must always consider shortened representations, usually involving recursion, to even being able to describe such numbers. One of the most known methodologies to conceive such numbers is using hyper-operations, that is a sequence of binary functions defined recursively starting from the usual chain: addition - multiplication - exponentiation. arXiv:1901.05372v2 [cs.LO] 12 Mar 2019 The most important notations to represent such hyper-operations have been considered by Knuth, Goodstein, Ackermann and Conway as described in this work’s introduction. Within this work we will give an axiomatic setup for this topic, and then try to find on one hand other ways to represent unimaginable numbers, as well as on the other hand applications to computer science, where the algorith- mic nature of representations and the increased computation capabilities of 1 computers give the perfect field to develop further the topic, exploring some possibilities to effectively operate with such big numbers.
    [Show full text]
  • Solving for the Unknown: Logarithms and Quadratics ID1050– Quantitative & Qualitative Reasoning Logarithms
    Solving for the Unknown: Logarithms and Quadratics ID1050– Quantitative & Qualitative Reasoning Logarithms Logarithm functions (common log, natural log, and their (evaluating) inverses) represent exponents, so they are the ‘E’ in PEMDAS. PEMDAS (inverting) Recall that the common log has a base of 10 • Parentheses • Log(x) = y means 10y=x (10y is also known as the common anti-log) Exponents Multiplication • Recall that the natural log has a base of e Division y y Addition • Ln(x) = y means e =x (e is also know as the natural anti-log) Subtraction Function/Inverse Pairs Log() and 10x LN() and ex Common Logarithm and Basic Operations • 2-step inversion example: 2*log(x)=8 (evaluating) PEMDAS • Operations on x: Common log and multiplication by 2 (inverting) • Divide both sides by 2: 2*log(x)/2 = 8/2 or log(x) = 4 Parentheses • Take common anti-log of both sides: 10log(x) = 104 or x=10000 Exponents Multiplication • 3-step inversion example: 2·log(x)-5=-4 Division Addition • Operations on x: multiplication, common log, and subtraction Subtraction • Add 5 to both sides: 2·log(x)-5+5=-4+5 or 2·log(x)=1 Function/Inverse Pairs 2·log(x)/2=1/2 log(x)=0.5 • Divide both sides by 2: or Log() and 10x • Take common anti-log of both sides: 10log(x) = 100.5 or x=3.16 LN() and ex Common Anti-Logarithm and Basic Operations • 2-step inversion example: 5*10x=6 (evaluating) PEMDAS x • Operations on x: 10 and multiplication (inverting) • Divide both sides by 5: 5*10x/5 = 6/5 or 10x=1.2 Parentheses • Take common log of both sides: log(10x)=log(1.2) or x=0.0792
    [Show full text]
  • Operation CLUE WORDS Remember, Read Each Question Carefully
    Operation CLUE WORDS Remember, read each question carefully. THINK about what the question is asking. Addition Subtraction add difference altogether fewer and gave away both take away in all how many more sum how much longer/ total shorter/smaller increase left less change Multiplication decrease each same twice Division product share equally in all (each) each double quotient every ©2012 Amber Polk-Adventures of a Third Grade Teacher Clue Word Cut and Paste Cut out the clue words. Sort and glue under the operation heading. Subtraction Multiplication Addition Division add each difference share equally both fewer in all twice product every gave away change quotient sum total left double less decrease increase ©2012 Amber Polk-Adventures of a Third Grade Teacher Clue Word Problems Underline the clue word in each word problem. Write the equation. Solve the problem. 1. Mark has 17 gum balls. He 5. Sara and her two friends bake gives 6 gumballs to Amber. a pan of 12 brownies. If the girls How many gumballs does Mark share the brownies equally, how have left? many will each girl have? 2. Lauren scored 6 points during 6. Erica ate 12 grapes. Riley ate the soccer game. Diana scored 3 more grapes than Erica. How twice as many points. How many grapes did both girls eat? many points did Diana score? 3. Kyle has 12 baseball cards. 7. Alice the cat is 12 inches long. Jason has 9 baseball cards. Turner the dog is 19 inches long. How many do they have How much longer is Turner? altogether? 4.
    [Show full text]
  • 1 Modular Arithmetic
    1 Modular Arithmetic Definition 1.1 (A divides B). Let A; B 2 Z. We say that A divides B (or A is a divisor of B), denoted AjB, if there is a number C 2 Z such that B = AC. Definition 1.2 (Prime number). Let P 2 N. We say that P is a prime number if P ≥ 2 and the only divisors of P are 1 and P . Definition 1.3 (Congruence modulo N). We denote by A mod N the remainder you get when you divide A by N. Note that A mod N 2 f0; 1; 2; ··· ;N − 1g. We say that A and B are congruent modulo N, denoted A ≡N B (or A ≡ B mod N), if A mod N = B mod N. Exercise 1.4. Show that A ≡N B if and only if Nj(A − B). Remark. The above characterization of A ≡N B can be taken as the definition of A ≡N B. Indeed, it is used a lot in proofs. Notation 1.5. We write gcd(A; B) to denote the greatest common divisor of A and B. Note that for any A, gcd(A; 1) = 1 and gcd(A; 0) = A. Definition 1.6 (Relatively prime). We say that A and B are relatively prime if gcd(A; B) = 1. Below, in Section 1.1, we first give the definitions of basic modular operations like addition, subtraction, multiplication, division and exponentiation. We also explore some of their properties. Later, in Section 1.2, we look at the computational complexity of these operations.
    [Show full text]
  • Multiplication Fact Strategies Assessment Directions and Analysis
    Multiplication Fact Strategies Wichita Public Schools Curriculum and Instructional Design Mathematics Revised 2014 KCCRS version Table of Contents Introduction Page Research Connections (Strategies) 3 Making Meaning for Operations 7 Assessment 9 Tools 13 Doubles 23 Fives 31 Zeroes and Ones 35 Strategy Focus Review 41 Tens 45 Nines 48 Squared Numbers 54 Strategy Focus Review 59 Double and Double Again 64 Double and One More Set 69 Half and Then Double 74 Strategy Focus Review 80 Related Equations (fact families) 82 Practice and Review 92 Wichita Public Schools 2014 2 Research Connections Where Do Fact Strategies Fit In? Adapted from Randall Charles Fact strategies are considered a crucial second phase in a three-phase program for teaching students basic math facts. The first phase is concept learning. Here, the goal is for students to understand the meanings of multiplication and division. In this phase, students focus on actions (i.e. “groups of”, “equal parts”, “building arrays”) that relate to multiplication and division concepts. An important instructional bridge that is often neglected between concept learning and memorization is the second phase, fact strategies. There are two goals in this phase. First, students need to recognize there are clusters of multiplication and division facts that relate in certain ways. Second, students need to understand those relationships. These lessons are designed to assist with the second phase of this process. If you have students that are not ready, you will need to address the first phase of concept learning. The third phase is memorization of the basic facts. Here the goal is for students to master products and quotients so they can recall them efficiently and accurately, and retain them over time.
    [Show full text]
  • Subtraction by Addition
    Memory & Cognition 2008, 36 (6), 1094-1102 doi: 10.3758/MC.36.6.1094 Subtraction by addition JAMIE I. D. CAMPBELL University of Saskatchewan, Saskatoon, Saskatchewan, Canada University students’ self-reports indicate that they often solve basic subtraction problems (13 6 ?) by reference to the corresponding addition problem (6 7 13; therefore, 13 6 7). In this case, solution latency should be faster with subtraction problems presented in addition format (6 _ 13) than in standard subtraction format (13 6 _). In Experiment 1, the addition format resembled the standard layout for addition with the sum on the right (6 _ 13), whereas in Experiment 2, the addition format resembled subtraction with the minuend on the left (13 6 _). Both experiments demonstrated a latency advantage for large problems (minuend 10) in the addition format as compared with the subtraction format (13 6 _), although the effect was larger in Experiment 1 (254 msec) than in Experiment 2 (125 msec). Small subtractions (minuend 10) in Experiment 1 were solved equally quickly in the subtraction or addition format, but in Experiment 2, performance on small problems was faster in the standard format (5 3 _) than in the addition format (5 3 _). The results indicate that educated adults often use addition reference to solve large simple subtraction problems, but that theyyy rely on direct memory retrieval for small subtractions. The cognitive processes that subserve performance of ementary arithmetic, small problems are often defined as elementary calculation (e.g., 2 6 8; 6 7 42) those with either a sum/minuend 10 (Seyler, Kirk, & have received extensive experimental analysis over the Ashcraft, 2003) or a product/dividend 25 (Campbell & last quarter century.
    [Show full text]