Modeling and Computation of Liquid Crystals
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Journal Abbreviations
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). not previously listed ⇤ The abbreviation is followed by the complete title, the place of publication journal indexed cover-to-cover § and other pertinent information. † monographic series Update date: July 1, 2016 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN Acta Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. § 1619-4500. ISSN 0236-5294. 29o Col´oq. Bras. Mat. 29o Col´oquio Brasileiro de Matem´atica. [29th Brazilian Acta Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue † § Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN o o † 30 Col´oq. Bras. Mat. 30 Col´oquio Brasileiro de Matem´atica. [30th Brazilian 1003-3998. ⇤ Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. Acta Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English § Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. † Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Acta Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). § Springer, Berlin. ISSN 1439-8516. † Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. Abh. Akad. Wiss. G¨ottingen Neue Folge Abhandlungen der Akademie der Acta Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. Chinese Series. † § Wissenschaften zu G¨ottingen. Neue Folge. [Papers of the Academy of Sciences Chinese Math. Soc., Acta Math. Sinica Ed. Comm., Beijing. ISSN 0583-1431. -

Reading List for Numerical Analysis Group D. Phil. Students MT 2013
Reading List for Numerical Analysis Group D. Phil. Students MT 2013 Each student should make a serious and continuing effort to familiarise himself/herself with the contents of several books from the following annotated list. The list is divided into subject areas and comments are given on the relative level and difficulty of each book. As a general rule, you should expect to study the most advanced books in the area of your dissertation together with a reasonable spread of books in related areas. A rough guide could be that you should be familiar with about a dozen books drawn from half a dozen of the listed areas. Journals Acta Numerica SIAM Review Journal of Computational Physics SIAM Journal on Numerical Analysis SIAM Journal on Matrix Analysis & Applications SIAM Journal on Scientific Computing SIAM Journal on Optimization BIT Numerical Mathematics Numerische Mathematik IMA Journal of Numerical Analysis Mathematics of Computation Foundations of Computational Mathematics Mathematical Programming Mathematical Programming Computation Floating point arithmetic M.L. Overton: Numerical Computing with IEEE Floating Point Arithmetic , SIAM, 2001. [Very readable and systematic presentation.] See also Chaps. 1 and 2 of the book by N.J. Higham listed below. Numerical linear algebra J.W. Demmel: Applied Numerical Linear Algebra, SIAM, 1997. [Best source on recent algorithms such as divide-and-conquer.] H.C. Elman, D.J. Silvester, A.J. Wathen: Finite Elements And Fast Iterative Solvers, Oxford University Press, 2005. [Major book at the interface of finite elements and matrix iterations.] G.H. Golub & C.F. Van Loan: Matrix Computations , Johns Hopkins, 4th ed. 2012. -

RESOURCES in NUMERICAL ANALYSIS Kendall E
RESOURCES IN NUMERICAL ANALYSIS Kendall E. Atkinson University of Iowa Introduction I. General Numerical Analysis A. Introductory Sources B. Advanced Introductory Texts with Broad Coverage C. Books With a Sampling of Introductory Topics D. Major Journals and Serial Publications 1. General Surveys 2. Leading journals with a general coverage in numerical analysis. 3. Other journals with a general coverage in numerical analysis. E. Other Printed Resources F. Online Resources II. Numerical Linear Algebra, Nonlinear Algebra, and Optimization A. Numerical Linear Algebra 1. General references 2. Eigenvalue problems 3. Iterative methods 4. Applications on parallel and vector computers 5. Over-determined linear systems. B. Numerical Solution of Nonlinear Systems 1. Single equations 2. Multivariate problems C. Optimization III. Approximation Theory A. Approximation of Functions 1. General references 2. Algorithms and software 3. Special topics 4. Multivariate approximation theory 5. Wavelets B. Interpolation Theory 1. Multivariable interpolation 2. Spline functions C. Numerical Integration and Differentiation 1. General references 2. Multivariate numerical integration IV. Solving Differential and Integral Equations A. Ordinary Differential Equations B. Partial Differential Equations C. Integral Equations V. Miscellaneous Important References VI. History of Numerical Analysis INTRODUCTION Numerical analysis is the area of mathematics and computer science that creates, analyzes, and implements algorithms for solving numerically the problems of continuous mathematics. Such problems originate generally from real-world applications of algebra, geometry, and calculus, and they involve variables that vary continuously; these problems occur throughout the natural sciences, social sciences, engineering, medicine, and business. During the second half of the twentieth century and continuing up to the present day, digital computers have grown in power and availability. -

Journal Abbreviations
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed E available electronically The abbreviation is followed by the complete title, the place of publication § journal reviewed cover-to-cover V videocassette series and other pertinent information. † monographic series ¶ bibliographic journal 4OR 4OR. Quarterly Journal of the Belgian, French and Italian Operations Research § E Acta Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English Series. Societies. Springer, Berlin. ISSN 1619-4500. Springer, Heidelberg. ISSN 0168-9673. ∗†19o Col´oq. Bras. Mat. 19o Col´oquio Brasileiro de Matem´atica. [19th Brazilian § E Acta Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o, Budapest. ISSN Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. 0236-5294. † 24o Col´oq. Bras. Mat. 24o Col´oquio Brasileiro de Matem´atica. [24th Brazilian §Acta Math. Inform. Univ. Ostraviensis Acta Mathematica et Informatica Universitatis Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. Ostraviensis. Univ. Ostrava, Ostrava. ISSN 1211-4774. ∗†25o Col´oq. Bras. Mat. 25o Col´oquio Brasileiro de Matem´atica. [25th Brazilian §Acta Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Wuli Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. (See also Acta † Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. Estonian Math.Sci.Ser.BEngl.Ed.) ISSN 1003-3998. Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. §ActaMath.Sci.Ser.BEngl.Ed. Acta Mathematica Scientia. Series B. English Edition. † Abh. Akad. Wiss. G¨ottingen. -

List of Mathematics Impact Factor Journals Indexed in ISI Web of Science (JCR SCI, 2016)
List of Mathematics Impact Factor Journals Indexed in ISI Web of Science (JCR SCI, 2016) Compiled by: Arslan Sheikh In Charge Reference & Research Section Library Information Services COMSATS Institute of Information Technology Park Road, Islamabad-Pakistan. Cell No +92-0321-9423071 [email protected] Rank Journal Title ISSN Impact Factor 1 ACTA NUMERICA 0962-4929 6.250 2 SIAM REVIEW 0036-1445 4.897 3 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY 0894-0347 4.692 4 Nonlinear Analysis-Hybrid Systems 1751-570X 3.963 5 ANNALS OF MATHEMATICS 0003-486X 3.921 6 COMMUNICATIONS ON PURE AND APPLIED MATHEMATICS 0010-3640 3.793 7 INTERNATIONAL JOURNAL OF ROBUST AND NONLINEAR CONTROL 1049-8923 3.393 8 ACM TRANSACTIONS ON MATHEMATICAL SOFTWARE 0098-3500 3.275 9 Publications Mathematiques de l IHES 0073-8301 3.182 10 INVENTIONES MATHEMATICAE 0020-9910 2.946 11 MATHEMATICAL MODELS & METHODS IN APPLIED SCIENCES 0218-2025 2.860 12 Advances in Nonlinear Analysis 2191-9496 2.844 13 FOUNDATIONS OF COMPUTATIONAL MATHEMATICS 1615-3375 2.829 14 Communications in Nonlinear Science and Numerical Simulation 1007-5704 2.784 15 FUZZY SETS AND SYSTEMS 0165-0114 2.718 16 APPLIED AND COMPUTATIONAL HARMONIC ANALYSIS 1063-5203 2.634 17 SIAM Journal on Imaging Sciences 1936-4954 2.485 18 ANNALES DE L INSTITUT HENRI POINCARE-ANALYSE NON LINEAIRE 0294-1449 2.450 19 ACTA MATHEMATICA 0001-5962 2.448 20 MATHEMATICAL PROGRAMMING 0025-5610 2.446 21 ARCHIVE FOR RATIONAL MECHANICS AND ANALYSIS 0003-9527 2.392 22 CHAOS 1054-1500 2.283 23 APPLIED MATHEMATICS LETTERS 0893-9659 -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed The abbreviation is followed by the complete title, the place of publication x journal indexed cover-to-cover and other pertinent information. y monographic series Update date: January 30, 2018 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN xActa Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English 1619-4500. Series. Springer, Heidelberg. ISSN 0168-9673. y 30o Col´oq.Bras. Mat. 30o Col´oquioBrasileiro de Matem´atica. [30th Brazilian xActa Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. ISSN 0236-5294. y Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. xActa Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN y Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. 1003-3998. y Abh. Akad. Wiss. G¨ottingenNeue Folge Abhandlungen der Akademie der xActa Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English Wissenschaften zu G¨ottingen.Neue Folge. [Papers of the Academy of Sciences Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. in G¨ottingen.New Series] De Gruyter/Akademie Forschung, Berlin. ISSN 0930- xActa Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). 4304. Springer, Berlin. ISSN 1439-8516. y Abh. Akad. Wiss. Hamburg Abhandlungen der Akademie der Wissenschaften xActa Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. -

D.B. Szyld Intro. to Numerical Alanalysis 22 October 2020 MATH 5043
D.B. Szyld Intro. to Numerical AlAnalysis 22 October 2020 MATH 5043 Literature Search Proposal expected on or before Tuesday 3 November. Report due on Thursday 12 November 2020, 5:00 p.m. You are requested to search in the literature for recent articles on any of the following topics: Floating point arithmetic, backward error analysis, interpolation, integration, solution of nonlinear equations (in particular variants of inexact Newton). You are expected to write a short report on the papers you find. I am asking you to read more than one paper. For example, two different approaches to the same problem, or three similar approaches by different authors. Choosing papers in the book reference list is discouraged. I would like to have a short proposal, listing the topic and the bibliography in 10 days or less. Then, you would write your short report, of say, three to five pages. Papers should be typed (LaTex is preferable). You should make a good effort to have a clear exposition of your ideas. Please, be critical, do not just copy what you read; in fact you are encouraged to discard some of the ideas if you find them inappropriate, or simply not great. Please explain your criteria and judgment. You will need to do some library work. A search such as the one I am propos- ing usually starts by looking at Mathematical Reviews, Computer Abstracts, or similar publications which list and reviews papers in a variety of journals. (Math. Rev. is available on line at http://www.ams.org/mathscinet or from the Temple Libraries Databases: https://guides.temple.edu/az.php). -

Listado De Revistas 2018 Revista Nombre Completo Clasificacion 1 Abstr
LISTADO DE REVISTAS 2018 REVISTA NOMBRE COMPLETO CLASIFICACION 1 ABSTR. APPL. ANAL. ABSTRACT AND APPLIED ANALYSIS R 2 ACTA APPL. MATH. ACTA APPLICANDAE MATHEMATICAE B 3 ACTA ARITH. ACTA ARITHMETICA B 4 ACTA MATH. ACTA MATHEMATICA MB 5 ACTA MATH. HUNGAR. ACTA MATHEMATICA HUNGARICA R 6 ACTA MATH. SCI. SER. B ENGL. ED. ACTA MATHEMATICA SCIENTIA. SERIES B. ENGLISH EDITION R 7 ACTA MATH. SIN. (ENGL. SER.) ACTA MATHEMATICA SINICA (ENGLISH SERIES) R 8 ACTA NUMER. ACTA NUMERICA MB 9 ADV. MODEL. OPTIM. ADVANCED MODELING AND OPTIMIZATION R 10 ADV. NONLINEAR STUD. ADVANCED NONLINEAR STUDIES B 11 ADV. APPL. CLIFFORD ALGEBR. ADVANCES IN APPLIED CLIFFORD ALGEBRAS R 12 ADV. IN APPL. MATH. ADVANCES IN APPLIED MATHEMATICS B 13 AAMM ADVANCES IN APPLIED MATHEMATICS AND MECHANICS R 14 ADV. IN APPL. PROBAB. ADVANCES IN APPLIED PROBABILITY B 15 ADV. IN CALCULUS OF VARIATIONS ADVANCES IN CALCULUS OF VARIATIONS B 16 ADV COMPUT MATH ADVANCES IN COMPUTATIONAL MATHEMATICS B 17 ADV. DIFFERENCE EQU. ADVANCES IN DIFFERENCE EQUATIONS R 18 ADV. DIFFERENTIAL EQUATIONS ADVANCES IN DIFFERENTIAL EQUATIONS B 19 ADV. GEOM. ADVANCES IN GEOMETRY B 20 ADV. MATH. SCI. APPL. ADVANCES IN MATHEMATICAL SCIENCES AND APPLICATIONS R 21 ADV. MATH. ADVANCES IN MATHEMATICS MB 22 ADVANCES IN PURE MATHEMATICS ADVANCES IN PURE MATHEMATICS R 23 AEQUATIONES MATH. AEQUATIONES MATHEMATICAE R ALEA LAT. AM. J. PROBAB. MATH. 24 ALEA. LATIN AMERICAN JOURNAL OF PROBABILITY AND MATHEMATICAL STATISTICS B STAT. 25 ALGEBR NUMBER THEORY ALGEBRA AND NUMBER THEORY MB 26 ALGEBRA COLLOQ. ALGEBRA COLLOQUIUM B 27 ALGEBRA UNIVERSALIS ALGEBRA UNIVERSALIS B 28 ALGEBR. GEOM. TOPOL. -

Tytuł 1 Punkty ACTA MATHEMATICA 200 ACTA NUMERICA 200
Tytuł 1 Punkty ACTA MATHEMATICA 200 ACTA NUMERICA 200 ADVANCES IN MATHEMATICS 200 AMERICAN JOURNAL OF MATHEMATICS 200 Analysis & PDE 200 ANNALES SCIENTIFIQUES DE L ECOLE NORMALE SUPERIEURE 200 ANNALS OF MATHEMATICS 200 ANNALS OF STATISTICS 200 BIOINFORMATICS 200 BULLETIN OF THE AMERICAN MATHEMATICAL SOCIETY 200 CALCULUS OF VARIATIONS AND PARTIAL DIFFERENTIAL EQUATIONS 200 COMMUNICATIONS ON PURE AND APPLIED MATHEMATICS 200 COMPOSITIO MATHEMATICA 200 DUKE MATHEMATICAL JOURNAL 200 FOUNDATIONS OF COMPUTATIONAL MATHEMATICS 200 GEOMETRIC AND FUNCTIONAL ANALYSIS 200 GEOMETRY & TOPOLOGY 200 INVENTIONES MATHEMATICAE 200 JOURNAL DE MATHEMATIQUES PURES ET APPLIQUEES 200 JOURNAL FUR DIE REINE UND ANGEWANDTE MATHEMATIK 200 JOURNAL OF ALGEBRAIC GEOMETRY 200 JOURNAL OF DIFFERENTIAL GEOMETRY 200 Journal of Mathematical Logic 200 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY 200 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION 200 JOURNAL OF THE EUROPEAN MATHEMATICAL SOCIETY 200 JOURNAL OF THE ROYAL STATISTICAL SOCIETY SERIES B-STATISTICAL METHODOLOGY 200 MATHEMATISCHE ANNALEN 200 MEMOIRS OF THE AMERICAN MATHEMATICAL SOCIETY 200 Probability Surveys 200 Publications Mathematiques de l IHES 200 SIAM REVIEW 200 Advances in Differential Equations 140 Algebra & Number Theory 140 ANNALES DE L INSTITUT FOURIER 140 ANNALES DE L INSTITUT HENRI POINCARE-ANALYSE NON LINEAIRE 140 ANNALI DELLA SCUOLA NORMALE SUPERIORE DI PISA-CLASSE DI SCIENZE 140 ANNALS OF APPLIED PROBABILITY 140 Annals of Mathematics Studies 140 ANNALS OF PROBABILITY 140 ANNALS OF PURE AND APPLIED -
List of Journals
Revised 29 March 2005 www.iee.org/inspec List of Journals Journal names prefixed with * are abstracted completely. Journal names prefixed with † are electronic-only publications. *(AI EDAM) Artificial Intelligence for Engineering *Acoustics Bulletin Design, Analysis and Manufacturing *Acoustics Research Letters Online 73 Amateur Radio Today Acquisitions Librarian AAVSO Circular *Acta Acustica ABA Bank Marketing *Acta Acustica United With Acustica ABA Banking Journal *Acta Astronomica ABB Review *Acta Astrophysica Sinica ABI-Technik *Acta Automatica Sinica Abstract and Applied Analysis *Acta Crystallographica, Section A (Foundations of *ABU Technical Review Crystallography) †Academic Open Internet Journal Acta Crystallographica, Section B (Structural Science) Academic Radiology Acta Crystallographica, Section C (Crystal Structure Academic Reports, Faculty of Engineering, Tokyo Communications) Institute of Polytechnics *Acta Crystallographica, Section D (Biological Academie des Sciences. Comptes Rendus, Crystallography) Mathematique †Acta Crystallographica, Section E (Structure Reports Academie des Sciences. Comptes Rendus, Physique Online) Academie Serbe des Sciences et des Arts Bulletin, *Acta Cybernetica Classe des Sciences Techniques *Acta Electronica Sinica Academie Serbe des Sciences et des Arts, Glas, Classe Acta Graphica des Sciences Techniques *Acta Informatica Academy of Management Journal Acta Manilana Academy of Management Review *Acta Materialia Accountancy Acta Mathematica Sinica Accounting Organizations and Society Acta Mathematicae -
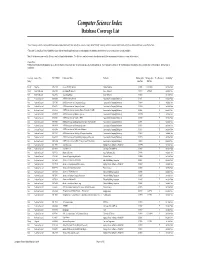
Computer Science Index Database Coverage List
Computer Science Index Database Coverage List "Core" coverage refers to sources which are indexed and abstracted in their entirety (i.e. cover to cover), while "Priority" coverage refers to sources which include only those articles which are relevant to the field. *Titles with 'Coming Soon' in the Availability column indicate that this publication was recently added to the database and therefore few or no articles are currently available. This title list does not represent the Selective content found in this database. The Selective content is chosen from thousands of titles containing articles that are relevant to this subject. Please Note: Publications included on this database are subject to change without notice due to contractual agreements with publishers. Coverage dates shown are the intended dates only and may not yet match those on the product. All coverage is cumulative. Coverage Source Type ISSN / ISBN Publication Name Publisher Bibliographic Bibliographic Peer-Reviewed Availability* Policy Start Date End Date Priority Magazine 1093-9105 Access-VB-SQL Advisor Advisor Media Inc 1/1/2000 12/31/2004 Available Now Priority Trade Publication 1068-6452 Accounting Technology SourceMedia, Inc. 7/1/1997 5/31/2009 Available Now Core Trade Publication 1044-5714 Accounting Today SourceMedia, Inc. 7/1/2003 Available Now Core Academic Journal 0360-0300 ACM Computing Surveys Association for Computing Machinery 1/1/1971 Y Available Now Core Academic Journal 1529-3785 ACM Transactions on Computational Logic Association for Computing Machinery -

Hans Z. Munthe-Kaas Professor, Dr.Ing
Curriculum Vitae: Hans Z. Munthe-Kaas Professor, Dr.Ing. Address Department of Mathematics, Phone (+47) 55584179 University of Bergen Email [email protected] P.O. Box 7803, Homepage hans.munthe-kaas.no 5020 Bergen, Norway Research IDs Google Scholar: Hans Munthe-Kaas th Born 28 March 1961, MathSciNet: 333145 Northallerton, UK ResearchGate: Hans Munthe-Kaas Sex Male ORCID: 0000-0002-4456-3150 Nationality Norwegian Education 1989 Dr.Ing. (PhD), Dept. of Mathematical Sciences, Norwegian Univ. of Science and Technology (NTNU). 1986 Siv.Ing. (MSc), Dept. of Mathematical Sciences, Norwegian Univ. of Science and Technology (NTNU). Employment History 2005 – pres. Professor, Department of Mathematics, University of Bergen 1997 – 2005 Professor (by calling), Department of Computer Science, University of Bergen 1991 – 1997 Associate professor, Department of Computer Science, University of Bergen 1996 – 2000 Adjunct prof. (Prof. II), Department of Mathematical Sciences, NTNU, Trondheim 1990 – 1995 Consulting scientist, SINTEF Industrial Mathematics, Trondheim 1990 – 1991 NAVF Post Doctoral Researcher, at CERFACS, Toulouse, France 1988 – 1990 Research scientist, SINTEF Industrial Mathematics, Trondheim, Norway 1986 – 1989 PhD Stipend, Department of Mathematical Sciences, NTNU, Trondheim Honors and awards 1995 Carl-Erik Fröberg Prize in Numerical analysis 1990 Exxon Mobile research award for best PhD, NTNU, 1989 1986 – 1989 Jubilee Scholar, NTNU, Trondheim, Norway (1 of 3 scholarships for 75th anniversary of NTNU) Elected memberships of academies 2016 Elected member The Norwegian Academy of Science and Letters 2012 Elected member The Royal Norwegian Society of Sciences and Letters (DKNVS) 2007 Elected member The Norwegian Academy of Technological Sciences (NTVA) Commissions of trust (recent) 2018 – 2022 Chair of the International Abel Prize Committee 2010 – 2018 Board of the Abel Prize in Mathematics 2017 – pres.