Lecture 29: Curl, Divergence and Flux
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Research Brief March 2017 Publication #2017-16
Research Brief March 2017 Publication #2017-16 Flourishing From the Start: What Is It and How Can It Be Measured? Kristin Anderson Moore, PhD, Child Trends Christina D. Bethell, PhD, The Child and Adolescent Health Measurement Introduction Initiative, Johns Hopkins Bloomberg School of Every parent wants their child to flourish, and every community wants its Public Health children to thrive. It is not sufficient for children to avoid negative outcomes. Rather, from their earliest years, we should foster positive outcomes for David Murphey, PhD, children. Substantial evidence indicates that early investments to foster positive child development can reap large and lasting gains.1 But in order to Child Trends implement and sustain policies and programs that help children flourish, we need to accurately define, measure, and then monitor, “flourishing.”a Miranda Carver Martin, BA, Child Trends By comparing the available child development research literature with the data currently being collected by health researchers and other practitioners, Martha Beltz, BA, we have identified important gaps in our definition of flourishing.2 In formerly of Child Trends particular, the field lacks a set of brief, robust, and culturally sensitive measures of “thriving” constructs critical for young children.3 This is also true for measures of the promotive and protective factors that contribute to thriving. Even when measures do exist, there are serious concerns regarding their validity and utility. We instead recommend these high-priority measures of flourishing -

College Summit, Inc. D/B/A Peerforward Financial Statements
College Summit, Inc. d/b/a PeerForward Financial Statements For the Years Ended April 30, 2020 and 2019 and Report Thereon COLLEGE SUMMIT, INC. d/b/a PeerForward TABLE OF CONTENTS For the Years Ended April 30, 2020 and 2019 _______________ Page Independent Auditors’ Report ............................................................................................................. 1-2 Financial Statements Statements of Financial Position ........................................................................................................ 3 Statements of Activities ...................................................................................................................... 4 Statements of Functional Expenses ................................................................................................ 5-6 Statements of Cash Flows .................................................................................................................. 7 Notes to Financial Statements ....................................................................................................... 8-17 INDEPENDENT AUDITORS’ REPORT To the Board of Directors of College Summit, Inc. d/b/a PeerForward Report on the Financial Statements We have audited the accompanying financial statements of College Summit, Inc. d/b/a PeerForward (PeerForward), which comprise the statements of financial position as of April 30, 2020 and 2019, and the related statements of activities, functional expenses and cash flows for the years then ended, and the related notes -

How Can We Create Environments Where Hate Cannot Flourish?
How can we create environments where hate cannot flourish? Saturday, February 1 9:30 a.m. – 10:00 a.m. Check-In and Registration Location: Field Museum West Entrance 10:00 a.m. – 10:30 a.m. Introductions and Program Kick-Off JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 10:30 a.m. – 11:30 a.m. Watch “The Path to Nazi Genocide” and Reflections JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 11:30 a.m. – 11:45 a.m. Break and walk to State of Deception 11:45 a.m. – 12:30 p.m. Visit State of Deception Interpretation by Holocaust Survivor Volunteers from the Illinois Holocaust Museum Location: Upper level 12:30 p.m. – 1:00 p.m. Breakout Session: Reflections on Exhibit Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B Saturday, February 2 (continued) 1:00 p.m. – 1:45 p.m. Lunch 1:45 p.m. – 2:45 p.m. A Survivor’s Personal Story Bob Behr, USHMM Survivor Volunteer Interviewed by: Ann Weber, USHMM Program Coordinator Location: Lecture Hall 1 2:45 p.m. – 3:00 p.m. Break 3:00 p.m. – 3:45 p.m. Student Panel: Beyond Indifference Location: Lecture Hall 1 Moderator: Emma Pettit, Sustained Dialogue Campus Network Student/Alumni Panelists: Jazzy Johnson, Northwestern University Mary Giardina, The Ohio State University Nory Kaplan-Kelly, University of Chicago 3:45 p.m. – 4:30 p.m. Breakout Session: Sharing Personal Reflections Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B 4:30 p.m. -

1 Curl and Divergence
Sections 15.5-15.8: Divergence, Curl, Surface Integrals, Stokes' and Divergence Theorems Reeve Garrett 1 Curl and Divergence Definition 1.1 Let F = hf; g; hi be a differentiable vector field defined on a region D of R3. Then, the divergence of F on D is @ @ @ div F := r · F = ; ; · hf; g; hi = f + g + h ; @x @y @z x y z @ @ @ where r = h @x ; @y ; @z i is the del operator. If div F = 0, we say that F is source free. Note that these definitions (divergence and source free) completely agrees with their 2D analogues in 15.4. Theorem 1.2 Suppose that F is a radial vector field, i.e. if r = hx; y; zi, then for some real number p, r hx;y;zi 3−p F = jrjp = (x2+y2+z2)p=2 , then div F = jrjp . Theorem 1.3 Let F = hf; g; hi be a differentiable vector field defined on a region D of R3. Then, the curl of F on D is curl F := r × F = hhy − gz; fz − hx; gx − fyi: If curl F = 0, then we say F is irrotational. Note that gx − fy is the 2D curl as defined in section 15.4. Therefore, if we fix a point (a; b; c), [gx − fy](a; b; c), measures the rotation of F at the point (a; b; c) in the plane z = c. Similarly, [hy − gz](a; b; c) measures the rotation of F in the plane x = a at (a; b; c), and [fz − hx](a; b; c) measures the rotation of F in the plane y = b at the point (a; b; c). -
FC = Mac V2 R V = 2Πr T F = T 1
Circular Motion Gravitron Cars Car Turning (has a curse) Rope Skip There must be a net inward force: Centripetal Force v2 F = maC a = C C R Centripetal acceleration 2πR v v v = R v T v 1 f = T The motorcycle rider does 13 laps in 150 s. What is his period? Frequency? R = 30 m [11.5 s, 0.087 Hz] What is his velocity? [16.3 m/s] What is his aC? [8.9 m/s2] If the mass is 180 kg, what is his FC? [1600 N] The child rotates 5 times every 22 seconds... What is the period? 60 kg [4.4 s] What is the velocity? [2.86 m/s] What is the acceleration? Which way does it point? [4.1 m/s2] What must be the force on the child? [245 N] Revolutions Per Minute (n)2πR v = 60 s An Ipod's hard drive rotates at 4200 RPM. Its radius is 0.03 m. What is the velocity in m/s of its edge? 1 Airplane Turning v = 232 m/s (520 mph) aC = 7 g's What is the turn radius? [785 m = 2757 ft] 2 FC Solving Circular Motion Problems 1. Determine FC (FBD) 2 2. Set FC = m v R 3. Solve for unknowns The book's mass is 2 kg it is spun so that the tension is 45 N. What is the velocity of the book in m/s? In RPM? R = 0.75 m [4.11 m/s] [52 RPM] What is the period (T) of the book? [1.15 s] The car is traveling at 25 m/s and the turn's radius is 63 m. -

Stroke Training for EMS Professionals (PDF)
STROKE TRAINING FOR EMS PROFESSIONALS 1 COURSE OBJECTIVES About Stroke Stroke Policy Recommendations Stroke Protocols and Stroke Hospital Care Stroke Assessment Tools Pre-Notification Stroke Treatment ABOUT STROKE STROKE FACTS • A stroke is a medical emergency! Stroke occurs when blood flow is either cut off or is reduced, depriving the brain of blood and oxygen • Approximately 795,000 strokes occur in the US each year • Stroke is the fifth leading cause of death in the US • Stroke is a leading cause of adult disability • On average, every 40 seconds, someone in the United States has a stroke • Over 4 million stroke survivors are in the US • The indirect and direct cost of stroke: $38.6 billion annually (2009) • Crosses all ethnic, racial and socioeconomic groups Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. DIFFERENT TYPES OF STROKE Ischemic Stroke • Caused by a blockage in an artery stopping normal blood and oxygen flow to the brain • 87% of strokes are ischemic • There are two types of ischemic strokes: Embolism: Blood clot or plaque fragment from elsewhere in the body gets lodged in the brain Thrombosis: Blood clot formed in an artery that provides blood to the brain Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. http://www.strokeassociation.org/STROKEORG/AboutStroke/TypesofStroke/IschemicClots/Ischemic-Strokes- Clots_UCM_310939_Article.jsp -

Curl, Divergence and Laplacian
Curl, Divergence and Laplacian What to know: 1. The definition of curl and it two properties, that is, theorem 1, and be able to predict qualitatively how the curl of a vector field behaves from a picture. 2. The definition of divergence and it two properties, that is, if div F~ 6= 0 then F~ can't be written as the curl of another field, and be able to tell a vector field of clearly nonzero,positive or negative divergence from the picture. 3. Know the definition of the Laplace operator 4. Know what kind of objects those operator take as input and what they give as output. The curl operator Let's look at two plots of vector fields: Figure 1: The vector field Figure 2: The vector field h−y; x; 0i: h1; 1; 0i We can observe that the second one looks like it is rotating around the z axis. We'd like to be able to predict this kind of behavior without having to look at a picture. We also promised to find a criterion that checks whether a vector field is conservative in R3. Both of those goals are accomplished using a tool called the curl operator, even though neither of those two properties is exactly obvious from the definition we'll give. Definition 1. Let F~ = hP; Q; Ri be a vector field in R3, where P , Q and R are continuously differentiable. We define the curl operator: @R @Q @P @R @Q @P curl F~ = − ~i + − ~j + − ~k: (1) @y @z @z @x @x @y Remarks: 1. -

Medical Terminology Abbreviations Medical Terminology Abbreviations
34 MEDICAL TERMINOLOGY ABBREVIATIONS MEDICAL TERMINOLOGY ABBREVIATIONS The following list contains some of the most common abbreviations found in medical records. Please note that in medical terminology, the capitalization of letters bears significance as to the meaning of certain terms, and is often used to distinguish terms with similar acronyms. @—at A & P—anatomy and physiology ab—abortion abd—abdominal ABG—arterial blood gas a.c.—before meals ac & cl—acetest and clinitest ACLS—advanced cardiac life support AD—right ear ADL—activities of daily living ad lib—as desired adm—admission afeb—afebrile, no fever AFB—acid-fast bacillus AKA—above the knee alb—albumin alt dieb—alternate days (every other day) am—morning AMA—against medical advice amal—amalgam amb—ambulate, walk AMI—acute myocardial infarction amt—amount ANS—automatic nervous system ant—anterior AOx3—alert and oriented to person, time, and place Ap—apical AP—apical pulse approx—approximately aq—aqueous ARDS—acute respiratory distress syndrome AS—left ear ASA—aspirin asap (ASAP)—as soon as possible as tol—as tolerated ATD—admission, transfer, discharge AU—both ears Ax—axillary BE—barium enema bid—twice a day bil, bilateral—both sides BK—below knee BKA—below the knee amputation bl—blood bl wk—blood work BLS—basic life support BM—bowel movement BOW—bag of waters B/P—blood pressure bpm—beats per minute BR—bed rest MEDICAL TERMINOLOGY ABBREVIATIONS 35 BRP—bathroom privileges BS—breath sounds BSI—body substance isolation BSO—bilateral salpingo-oophorectomy BUN—blood, urea, nitrogen -

Teresa Blackford V. Welborn Clinic
IN THE Indiana Supreme Court Supreme Court Case No. 21S-CT-85 Teresa Blackford Appellant (Plaintiff below) –v– Welborn Clinic Appellee (Defendant below) Argued: April 22, 2021 | Decided: August 31, 2021 Appeal from the Vanderburgh Circuit Court No. 82C01-1804-CT-2434 The Honorable David D. Kiely, Judge On Petition to Transfer from the Indiana Court of Appeals No. 19A-CT-2054 Opinion by Justice Goff Chief Justice Rush and Justices David, Massa, and Slaughter concur. Goff, Justice. Statutory limitations of action are “fundamental to a well-ordered judicial system.” See Bd. of Regents of Univ. of State of N. Y. v. Tomanio, 446 U.S. 478, 487 (1980). The process of discovery and trial, revealing ultimate facts that either help or harm the plaintiff, are “obviously more reliable if the witness or testimony in question is relatively fresh.” Id. And potential defendants, of course, seek to avoid indefinite liability for past conduct. C. Corman, 1 Limitation of Actions § 1.1, at 5 (1991). Naturally, then, “there comes a point at which the delay of a plaintiff in asserting a claim is sufficiently likely either to impair the accuracy of the fact-finding process or to upset settled expectations that a substantive claim will be barred” regardless of its merit. Tomanio, 446 U.S. at 487. At the same time, most courts recognize that certain circumstances may “justify an exception to these strong policies of repose,” extending the time in which a plaintiff may file a claim—a process known as “tolling.” Id. at 487–88. The circumstances here present us with these competing interests: the plaintiff, having been misinformed of a medical diagnosis by her provider, which dissolved its business more than five years prior to the plaintiff filing her complaint, seeks relief for her injuries on grounds of fraudulent concealment, despite expiration of the applicable limitation period. -
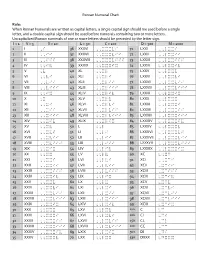
Roman Numeral Chart
Roman Numeral Chart Rule: When Roman Numerals are written as capital letters, a single capital sign should me used before a single letter, and a double capital sign should be used before numerals containing two or more letters. Uncapitalized Roman numerals of one or more letters should be preceded by the letter sign. I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 1 I ,I 36 XXXVI ,,XXXVI 71 LXXI ,,LXXI 2 II ,,II 37 XXXVII ,,XXXVII 72 LXXII ,,LXXII 3 III ,,III 38 XXXVIII ,,XXXVIII 73 LXXIII ,,LXXIII 4 IV ,,IV 39 XXXIX ,,XXXIX 74 LXXIV ,,LXXIV 5 V ,V 40 XL ,,XL 75 LXXV ,,LXXV 6 VI ,,VI 41 XLI ,,XLI 76 LXXVI ,,LXXVI 7 VII ,,VII 42 XLII ,,XLII 77 LXXVII ,,LXXVII 8 VIII ,,VIII 43 XLIII ,,XLIII 78 LXXVIII ,,LXXVIII 9 IX ,,IX 44 XLIV ,,XLIV 79 LXXIX ,,LXXIX 10 X ,X 45 XLV ,,XLV 80 LXXX ,,LXXX 11 XI ,,XI 46 XLVI ,,XLVI 81 LXXXI ,,LXXXI 12 XII ,,XII 47 XLVII ,,XLVII 82 LXXXII ,,LXXXII 13 XIII ,,XIII 48 XLVIII ,,XLVIII 83 LXXXIII ,,LXXXIII 14 XIV ,,XIV 49 XLIX ,,XLIX 84 LXXXIV ,,LXXXIV 15 XV ,,XV 50 L ,,L 85 LXXXV ,,LXXXV 16 XVI ,,XVI 51 LI ,,LI 86 LXXXVI ,,LXXXVI 17 XVII ,,XVII 52 LII ,,LII 87 LXXXVII ,,LXXXVII 18 XVIII ,,XVIII 53 LIII ,,LIII 88 LXXXVIII ,,LXXXVIII 19 XIX ,,XIX 54 LIV ,,LIV 89 LXXXIX ,,LXXXIX 20 XX ,,XX 55 LV ,,LV 90 XC ,,XC 21 XXI ,,XXI 56 LVI ,,LVI 91 XCI ,,XCI 22 XXII ,,XXII 57 LVII ,,LVII 92 XCII ,XCII 23 XXIII ,,XXIII 58 LVIII ,,LVIII 93 XCIII ,XCIII 24 XXIV ,,XXIV 59 LIX ,,LIX 94 XCIV ,XCIV 25 XXV ,,XXV 60 LX ,,LX 95 XCV ,XCV 26 XXVI ,,XXVI 61 LXI ,,LXI 96 XCVI ,XCVI 27 XXVII ,,XXVII 62 LXII ,,LXII 97 XCVII ,XCVII 28 XXVIII ,,XXVIII 63 LXIII ,,LXIII 98 XCVIII ,XCVIII 29 XXIX ,,XXIX 64 LXIV ,,LXIV 99 XCIX ,XCIX 30 XXX ,,XXX 65 LXV ,,LXV 100 C ,C 31 XXXI ,,XXXI 66 LXVI ,,LXVI 101 CI ,CI 32 XXXII ,,XXXII 67 LXVII ,,LXVII 150 CL ,CL 33 XXXIII ,,XXXIII 68 LXVIII ,,LXVIII 200 CC ,CC 34 XXXIV ,,XXXIV 69 LXIX ,,LXIX 501 DI ,DI 35 XXXV ,,XXXV 70 LXX ,,LXX 530 DXXX ,DXXX . -

Chapter 3 Motion in Two and Three Dimensions
Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a. -

Linear Functions. Definition. Suppose V and W Are Vector Spaces and L
Linear functions. Definition. Suppose V and W are vector spaces and L : V → W. (Remember: This means that L is a function; the domain of L equals V ; and the range of L is a subset of W .) We say L is linear if L(cv) = cL(v) whenever c ∈ R and v ∈ V and L(v1 + v2) = L(v1) + L(v2) whenever v1, v2 ∈ V . We let ker L = {v ∈ V : L(v) = 0} and call ker L the kernel of L and we let rng L = {L(v): v ∈ V } so rng L is the range of L. We let L(V, W ) be the set of L such that L : V → W and L is linear. Example. Suppose m and n are positive integers and L ∈ L(Rn, Rm). For each i = 1, . , m and each j = 1, . , n we let i lj be the i-th component of L(ej). Thus Xm 1 m i L(ej) = (lj , . , lj ) = ljei whenever j = 1, . , n. i=1 n Suppose x = (x1, . , xn) ∈ R . Then Xn x = xjej j=1 so à ! 0 1 Xn Xn Xn Xn Xm Xm Xn i @ i A L(x) = L( xjej) = L(xjej) = xjL(ej) = xj ljei = xjlj ei. j=1 j=1 j=1 j=1 i=1 i=1 j=1 We call 2 1 1 1 3 l1 l2 ··· ln 6 7 6 2 1 2 7 6 l1 22 ··· ln 7 6 7 6 . .. 7 4 . 5 m m m l1 l2 ··· ln the standard matrix of L.