Back-Testing of Trading Strategies Using Financial Crisis Observatory
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-
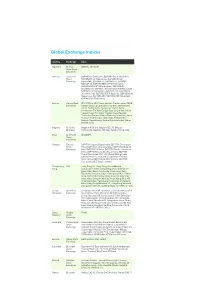
Global Exchange Indices
Global Exchange Indices Country Exchange Index Argentina Buenos MERVAL, BURCAP Aires Stock Exchange Australia Australian S&P/ASX All Ordinaries, S&P/ASX Small Ordinaries, Stock S&P/ASX Small Resources, S&P/ASX Small Exchange Industriials, S&P/ASX 20, S&P/ASX 50, S&P/ASX MIDCAP 50, S&P/ASX MIDCAP 50 Resources, S&P/ASX MIDCAP 50 Industrials, S&P/ASX All Australian 50, S&P/ASX 100, S&P/ASX 100 Resources, S&P/ASX 100 Industrials, S&P/ASX 200, S&P/ASX All Australian 200, S&P/ASX 200 Industrials, S&P/ASX 200 Resources, S&P/ASX 300, S&P/ASX 300 Industrials, S&P/ASX 300 Resources Austria Vienna Stock ATX, ATX Five, ATX Prime, Austrian Traded Index, CECE Exchange Overall Index, CECExt Index, Chinese Traded Index, Czech Traded Index, Hungarian Traded Index, Immobilien ATX, New Europe Blue Chip Index, Polish Traded Index, Romanian Traded Index, Russian Depository Extended Index, Russian Depository Index, Russian Traded Index, SE Europe Traded Index, Serbian Traded Index, Vienna Dynamic Index, Weiner Boerse Index Belgium Euronext Belgium All Share, Belgium BEL20, Belgium Brussels Continuous, Belgium Mid Cap, Belgium Small Cap Brazil Sao Paulo IBOVESPA Stock Exchange Canada Toronto S&P/TSX Capped Equity Index, S&P/TSX Completion Stock Index, S&P/TSX Composite Index, S&P/TSX Equity 60 Exchange Index S&P/TSX 60 Index, S&P/TSX Equity Completion Index, S&P/TSX Equity SmallCap Index, S&P/TSX Global Gold Index, S&P/TSX Global Mining Index, S&P/TSX Income Trust Index, S&P/TSX Preferred Share Index, S&P/TSX SmallCap Index, S&P/TSX Composite GICS Sector Indexes -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

Execution Version
Execution Version GUARANTEED SENIOR SECURED NOTES PROGRAMME issued by GOLDMAN SACHS INTERNATIONAL in respect of which the payment and delivery obligations are guaranteed by THE GOLDMAN SACHS GROUP, INC. (the “PROGRAMME”) PRICING SUPPLEMENT DATED 23rd SEPTEMBER 2020 SERIES 2020-12 SENIOR SECURED EXTENDIBLE FIXED RATE NOTES (the “SERIES”) ISIN: XS2233188510 Common Code: 223318851 This document constitutes the Pricing Supplement of the above Series of Secured Notes (the “Secured Notes”) and must be read in conjunction with the Base Listing Particulars dated 25 September 2019, as supplemented from time to time (the “Base Prospectus”), and in particular, the Base Terms and Conditions of the Secured Notes, as set out therein. Full information on the Issuer, The Goldman Sachs Group. Inc. (the “Guarantor”), and the terms and conditions of the Secured Notes, is only available on the basis of the combination of this Pricing Supplement and the Base Listing Particulars as so supplemented. The Base Listing Particulars has been published at www.ise.ie and is available for viewing during normal business hours at the registered office of the Issuer, and copies may be obtained from the specified office of the listing agent in Ireland. The Issuer accepts responsibility for the information contained in this Pricing Supplement. To the best of the knowledge and belief of the Issuer and the Guarantor the information contained in the Base Listing Particulars, as completed by this Pricing Supplement in relation to the Series of Secured Notes referred to above, is true and accurate in all material respects and, in the context of the issue of this Series, there are no other material facts the omission of which would make any statement in such information misleading. -

Ned Davis Research Group
Ned Davis Research Group THE OUTLooK FOR StoCKS, CoMMODITIES, AND GLOBAL THEMES: SECULAR AND CYCLICAL INFLUENCES Atlanta MTA & CFA Society of Atlanta | September 24, 2008 Tim Hayes, CMT, Chief Investment Strategist The NDR Approach • Identify investment themes and stay with them until a sentiment extreme is reached. • We say… » "Go with the flow until it reaches an extreme and then reverses." » "The big money is made on the big moves." » "Let your profits run, cut your losses short." • We develop reliable indicators and models based on… » "The Tape" – Trend, momentum, confirmation & divergence. » Investor psychology – Sentiment and valuation extremes. » Liquidity – Monetary and economic conditions, supply & demand. • In summary, NDR approach is… » Objective » Disciplined » Risk-Averse » Flexible 1 Ned Davis Research Group Please see important disclosures at the end of this document. CURRENT POSITIONS Global Allocation: Overweight/Bullish: Underweight/Bearish: Stocks » Bonds (by 10%) » Stocks (by 15%) Cash 40% » Cash (by 5%) 15% Bonds 45% » Pacific ex. Japan » U.K. » U.S. » Japan U.S. Allocation: Stocks 40% Cash 20% » Cash (by 10%) » Stocks (by 15%) » Bonds (by 5%) Bonds 40% Styles: » Growth » Value Sectors: » Energy » Consumer Discretionary » Basic Resources » Financials » Consumer Staples » Utilities Commodities: » Correction within secular uptrend Bonds: » 105% of benchmark duration Neutral Positions: » Large-caps vs. Small-caps » Yield curve 2 Ned Davis Research Group Please see important disclosures at the end of this document. We've -

Cointegration of International Stock Markets: an Investigation of Diversification Opportunities
Cointegration of International Stock Markets: An Investigation of Diversification Opportunities Taimur Ali Khan February 2011 Comprehensive Exercise in Economics Carleton College Advisor: Pavel Kapinos Abstract: This paper examines the long-run convergence of the United States and 22 other developed and developing countries. I use daily data and run the Johansen (1988) and the Gregory and Hansen (1996) test to show that stock markets of most countries have become cointegrated by 2010. I also look at short- run diversification opportunities across the countries by comparing their daily returns to the daily returns of the global index (S&P 1200). China, Malaysia and Austria stand out as countries with highly favorable diversification opportunities as they are not cointegrated about with the US and are insensitive to the global index. Finally, I use the relative risk of each country (obtained from the CAPM model) to measure performance of each country over the great recession of the 2000s. I find that the relative risk of a country is a good predictor of country performance in a recession. JEL Categories: C-22, F-36, G-15 Keywords: Stock market integration, Long‐run convergence, Cointegration, Portfolio diversification, Capital Asset Pricing Model 1 1. Introduction One of the fundamental tenants of investing is holding a diversified portfolio of securities and reducing one’s exposure to risk. Consequently, fund managers are always on the look-out for securities that do not correlate together and hence provide for better opportunities to hedge risk. In recent years that has meant moving beyond the confines of one’s borders and investing in other countries as well. -

AUSTRIA.EU.NFRD.2019.10.01.Pdf
Copyright © Development International e.V., 2019 ISBN: 978-3-9820398-3-1 Authors: Chris N. Bayer, PhD Juan Ignacio Ibañez, LL.M. Jiahua (Java) Xu, PhD Title: A New Responsibility for Sustainability: Corporate Non-Financial Reporting in Austria Date published: October 1, 2019 Funded by: iPoint-systems gmbh www.ipoint-systems.com Executive Summary The EU Non-Financial Reporting Directive (NFRD) is a new regulation that seeks to “increase the relevance, consistency and comparability of information disclosed by certain large undertakings and groups across the Union.”1 Large undertakings in EU member states are not only required to report on their financial basics, now they are also required by Article 1 of the Directive to disclose their non-financial performance relevant to their business impact. This would include adverse consequences they have notably on the environment, labor rights, human rights, and how they handle diversity matters and the risk of corruption, whether as a function of their own business or actors in their supply chains. “You manage what you measure.” In accordance with the Directive, the Austrian transposition stipulates that the non-financial declaration must state which reporting framework was used to create it, as well as apply non-financial key performance indicators relevant to the particular business. These requirements are the impetus behind this study and our point of departure: We systematically assess the degree of non-financial transparency and performance reporting for 2018, applying an ex-post assessment framework premised on reporting frameworks as per the Global Reporting Initiative (GRI) and the United Nations Global Compact (UNGC). By benchmarking all Austrian companies subject to the EU NFRD-transposed law on the topics required to be disclosed – environmental, human rights, employee, social (gender), and anti-corruption matters – this study reveals which companies make an effort to show their degree of responsibility, and to what degree. -

Volume 37, Issue 3
Volume 37, Issue 3 A fractal analysis of world stock markets Taro Ikeda Graduate School of Economics, Kobe University Abstract This paper provides a fractal analysis of world stock prices. We find that the majority of stock prices are fractal. Citation: Taro Ikeda, (2017) ''A fractal analysis of world stock markets'', Economics Bulletin, Volume 37, Issue 3, pages 1514-1532 Contact: Taro Ikeda - [email protected]. Submitted: December 22, 2016. Published: July 02, 2017. 1 Introduction The recent financial crisis suggests the failure of the rational expectations of economic agents. Rational expectations are a key concept for the efficient market hypothesis (i.e., the random walk model), where rational agents process all available information to form- ing stock price forecasts, and therefore prices only change in response to new shocks, and are not correlated with past shocks. This paper contributes to the macroeconomics literature using the fractal geome- try established by Benoit, B., Mandelbrot.1 The important difference between fractal geometry and the random walk is the assumption surrounding the distribution. A bell- shaped distribution for the random walk cannot account for the risk associated with very large deviations of stock prices from their mean values, and therefore the efficient mar- ket hypothesis fails to consider the big-break-down of the stock markets. However, the power-law distribution used in fractal geometry gives large deviations higher probabilities and can capture black swan events more easily than can the random walk model. This paper provides a fractal analysis of world stock markets to test the efficient market hypothesis empirically. -

3. ETF Performances
FOR MARKETING PURPOSE Lyxor ETF Monthly Report - Important information on risk factors, please refer to page 2 30th December 2020 Lyxor ATX (DR) UCITS ETF 1. FUND INFORMATION Ticker: CBATX SW Investment objective Main Fund Characteristics The Lyxor ATX (DR) UCITS ETF is a UCITS compliant exchange traded fund that aims to track the benchmark index ATX Total Return. Ticker CBATX SW The ATX Total Return (Austrian Traded index) is a capitalisation-weighted price index and currently consists of the 20 Fund Type SICAV Austrian blue-chip stocks with the highest turnover. Each shares weight is capped at 20%. The index is published by the Domiciliation Luxembourg Vienna Stock Exchange real time in EUR. The ATX® is designed as a tradeable index and is used as the underlying UCITS compliant Yes security for futures, options and structured products. The starting level of the ATX® was set at 1,000 index points on 2 ISIN LU0392496690 January 1991. The ATX® is calculated as a price index. Swiss Tax Yes Replication method Direct (physical) Trading Information Sampling No Securities Lending No Opening Hours Distri- Place Currency Ticker Bloomberg (GMT) bution Share Class Currency EUR Inception Date 01/12/2008 SIX Swiss Exchange 08:00 / 16:20 CHF CBATX SW Yes Nav per share at inception (EUR) 18.011 Deutsche Boerse (Xetra)* 08:00 / 19:00 EUR CBATX GY Yes SIX Swiss Exchange 08:00 / 16:20 EUR CBATXEU SW Yes Total Expense Ratio p.a 0.25% * First Listing Place of this share class Currency risk Yes NAV per Share ( EUR ) 32.39 Share AUM ( M EUR) 11.47 Total Fund Assets ( M EUR ) 11.47 Umbrella ( M EUR ) 6,752.67 Minimum Investment (Share) 1 Income treatment Distribution Last Amount (EUR) 0.59 Source: Lyxor AM, 30th December 2020 2. -
Anxiety for the Pandemic and Trust in Financial Markets
Anxiety for the pandemic and trust in financial markets∗ Roy Cerqueti1;2y Valerio Ficcadenti1 1 School of Business London South Bank University London, SE1 0AA, UK [email protected] (V. Ficcadenti); [email protected] (R. Cerqueti) 2 Department of Social and Economic Sciences Sapienza University of Rome Rome, I-00185, Italy [email protected] Abstract The COVID-19 pandemic has generated disruptive changes in many fields. Here we focus on the relationship between the anxiety felt by people during the pandemic and the trust in the future performance of financial markets. Precisely, we move from the idea that the volume of Google searches about \coronavirus" can be considered as a proxy of the anxiety and, jointly with the stock index prices, can be used to produce mood indicators { in terms of pessimism and optimism { at country level. We analyse the \very high human developed countries" according to the Human Development Index plus China and their respective main stock market indexes. Namely, we propose both a temporal and a global measure of pessimism and optimism and provide accordingly a classification of indexes and countries. The results show the existence of different clusters of countries and markets in terms of pes- simism and optimism. Moreover, specific regimes along the time emerge, with an increasing arXiv:2008.01649v1 [q-fin.ST] 1 Aug 2020 optimism spreading during the mid of June 2020. Furthermore, countries with different gov- ernment responses to the pandemic have experienced different levels of mood indicators, so that countries with less strict lockdown had a higher level of optimism. -
Annual Report 2009 of the Mayr-Melnhof Group
Annual Report 09 The Mayr-Melnhof Group Overview consolidated (in millions of EUR) 2009 2008 +/- Consolidated sales 1,601.5 1,731.2 -7.5 % EBITDA 229.7 216.3 +6.2 % Operating profit 149.9 136.9 +9.5 % Profit before tax 132.4 138.0 -4.1 % Profit for the year 97.4 96.9 +0.5 % Cash earnings 184.9 175.6 +5.3 % Return on equity 10.4 % 10.5 % Operating margin 9.4 % 7.9 % Return on capital employed 16.9 % 16.1 % Total equity 964.3 913.7 Total assets 1,391.8 1,425.9 Capital expenditures 61.6 96.7 Depreciation and amortization 97.8 83.5 Employees 8,112 8,240 Earnings per share (in EUR) 4.44 4.38 Dividend per share (in EUR) 1.701) 1.70 1) proposed The Mayr-Melnhof Group Business Structure ~1.6 million tons of fiber Consumer goods producers (80 % recovered fiber) ~220,000 tons of Production of cartonboard from MMK ~630,000 tons ~1.5 million tons of cartonboard processed of cartonboard (2009) (2009) Folding carton ~410,000 tons manufacturers of recycled and virgin fiber based cartonboard Basis 2009 Overview Group sales by destination Sales/Operating margin 1,750 17.0 % Western Europe 69 % 1,500 15.0 % 1,250 12.5 % 1,000 10.0 % Eastern Europe 23 % 750 7.5 % 500 5.0 % 250 2.5 % Asia 4 % in millions of EUR in % Other 4 % 2005 2006 2007 2008 2009 Basis 2009 Sales Operating margin Cash earnings Earnings per share and dividend per share 200 5.0 4.5 4.0 150 3.5 3.0 100 2.5 2.0 1.5 50 1.0 0.5 in millions of EUR in EUR 2005 2006 2007 2008 2009 2005 2006 2007 2008 20091) Earnings per share Dividend per share 1) proposed The Mayr-Melnhof Group The Mayr-Melnhof Group is the world’s largest producer of recycled cartonboard with a rising position in virgin fiber based board and the leading European manufac- turer of folding cartons. -
Impact of CSR-Relevant News on Stock Prices of Companies Listed in the Austrian Traded Index (ATX)
International Journal of Financial Studies Article Impact of CSR-Relevant News on Stock Prices of Companies Listed in the Austrian Traded Index (ATX) Manuela Ender 1,* and Finn Brinckmann 2 1 Campus Urstein, Salzburg University of Applied Sciences, Urstein Süd 1, 5412 Puch/Salzburg, Austria 2 Biogena Management Holding GmbH, Strubergasse 24, 5020 Salzburg, Austria * Correspondence: [email protected]; Tel.: +43-50-2211-1126 Received: 7 February 2019; Accepted: 18 June 2019; Published: 28 June 2019 Abstract: This paper examines the short-term influence of CSR-relevant news on the enterprise value in the form of respective shareholder value, which is represented by the corresponding stock price. This effect is measured using an event study applied to companies in the “Austrian Traded Index” (ATX). Subsequently, the results of the study show that CSR-relevant news in the financial portal finanzen.net trigger statistically significant abnormal returns and average cumulated abnormal returns within a period of five days. Based on these research results, it is stated that CSR-relevant news has a significant impact on the shareholder value of a company represented by its stock price. The hypotheses defined on the basis of the previously conducted studies on this topic were only partially confirmed. In particular, the negative effects of negative CSR-relevant news are insufficiently shown. Based on these findings, it can be deduced that the effects of the news are reinforced by the CSR relevance, although media presence due to the publications is a factor to be explored. Keywords: corporate social responsibility; CSR-relevant news; event study; Austrian Traded Index JEL Classification: G14; G32; Q56 1. -

Adoption of Identity Theft Countermeasures and Its Short- and Long-Term Impact on Firm Value
RESEARCH NOTE ADOPTION OF IDENTITY THEFT COUNTERMEASURES AND ITS SHORT- AND LONG-TERM IMPACT ON FIRM VALUE Indranil Bose Indian Institute of Management Calcutta, Diamond Harbor Road, Kolkata 700104 INDIA {[email protected]} Alvin Chung Man Leung Department of Information Systems, College of Business, City University of Hong Kong, Tat Chee Avenue, Kowloon, HONG KONG {[email protected]} Appendix A Previous Research on Ascertaining Value of IT Investment Using Event Studies Previous studies on IT investment using event studies investigated different aspects of IT. For example, Dos Santos et al. (1993) studied IT innovativeness and Chatterjee et al. (2002) focused on different functionality aspects of IT (e.g., infrastructure and application). Apart from general IT investment, there were also a few studies specific to IT applications (e.g., ERP, e-business, and security). Nevertheless, the steps of the event study adopted in previous studies were similar. All previous studies first analyzed abnormal return based on subsamples followed by subsampling analysis. Most studies adopted a three-day event window around IT investment announcements. Both parametric and non- parametric tests (e.g., sign test and Corrado’s rank test) were used to determine the level of significance of abnormal return in the estimation period. Furthermore, most of the sample data were from the United States. Meng and Lee (2007) was the only study that compared the reaction of IT investment in the United States with that in China. A summary of previous research on IT investment using event studies is shown in Table A1. MIS Quarterly Vol. 43 No. 1—Appendices/March 2019 A1 Bose & Leung/Adoption of Identity Theft Countermeasures Table A1.