Introducton to Algorithms and Implementations: Three Simple
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pyqgis Testing Developer Cookbook
PyQGIS testing developer cookbook QGIS Project Sep 25, 2021 CONTENTS 1 Introduction 1 1.1 Scripting in the Python Console ................................... 1 1.2 Python Plugins ............................................ 2 1.2.1 Processing Plugins ...................................... 3 1.3 Running Python code when QGIS starts ............................... 3 1.3.1 The startup.py file ................................... 3 1.3.2 The PYQGIS_STARTUP environment variable ...................... 3 1.4 Python Applications ......................................... 3 1.4.1 Using PyQGIS in standalone scripts ............................. 4 1.4.2 Using PyQGIS in custom applications ............................ 5 1.4.3 Running Custom Applications ................................ 5 1.5 Technical notes on PyQt and SIP ................................... 6 2 Loading Projects 7 2.1 Resolving bad paths .......................................... 8 3 Loading Layers 9 3.1 Vector Layers ............................................. 9 3.2 Raster Layers ............................................. 12 3.3 QgsProject instance .......................................... 14 4 Accessing the Table Of Contents (TOC) 15 4.1 The QgsProject class ......................................... 15 4.2 QgsLayerTreeGroup class ...................................... 16 5 Using Raster Layers 19 5.1 Layer Details ............................................. 19 5.2 Renderer ............................................... 20 5.2.1 Single Band Rasters .................................... -

Guide Pédagogique
2de SCIENCES NUMÉRIQUES ET TECHNOLOGIE GUIDE PÉDAGOGIQUE foucherconnect.fr Dans ce manuel, des ressources en accès direct pour tous SCIENCES NUMÉRIQUES ET TECHNOLOGIE 2de GUIDE PÉDAGOGIQUE Coordination : Dominique Lescar Cédric Blivet, professeur de sciences de l’ingénieur, lycée Gustave Monod Enghien-les-Bains (95) Fabrice Danes, professeur de sciences de l’ingénieur, lycée Pierre Mendès-France, Rennes (35) Hassan Dibesse, professeur de sciences de l’ingénieur, lycée Lesage, Vannes (56) Patricia Kerner, professeure de sciences de l’ingénieur, lycée Yves Thépot, Quimper (29) Yannig Salaun, professeur de mathématiques, lycée de l’Élorn, Landerneau (29) Édition : Emmanuelle Mary Mise en page : Grafatom « Le photocopillage, c’est l’usage abusif et collectif de la photocopie sans auto- risation des auteurs et des éditeurs. Largement répandu dans les établissements d’enseignement, le photocopillage menace l’avenir du livre, car il met en danger son équilibre économique. Il prive les auteurs d’une juste rémunération. En dehors de l’usage privé du copiste, toute reproduction totale ou partielle de cet ouvrage est interdite. » ISBN : 978-2-216-15505-7 Toute reproduction ou représentation intégrale ou partielle, par quelque procédé que ce soit, des pages publiées dans le présent ouvrage, faite sans autorisation de l’éditeur ou du Centre français du Droit de copie (20, rue des Grands-Augustins, 75006 Paris), est illicite et constitue une contrefaçon. Seules sont autorisées, d’une part, les reproductions strictement réservées à l’usage privé du copiste et non destinées à une utilisation collective, et, d’autre part, les analyses et courtes citations justifiées par le caractère scien- tifique ou d’information de l’œuvre dans laquelle elles sont incorporées (Loi du 1er juillet 1992 - art. -

Το Παιχνιδι ‘Binary Droids’»
Α ΡΙΣΤΟΤΕΛΕΙΟ Π ΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΣΤΡΑΝΤΖΗ ΑΝΤΩΝΙΑ Α.Ε.Μ. 2090 «ΑΝΑΠΤΥΞΗ ΠΑΙΧΝΙΔΙΩΝ ΜΑΘΗΣΗΣ ΣΕ ΓΛΩΣΣΑ PYTHON: ΤΟ ΠΑΙΧΝΙΔΙ ‘BINARY DROIDS’» (Learning Games Development in Python: The ‘Binary Droids’ Game) ΕΠΙΒΛΕΠΩΝ ΚΑΘΗΓΗΤΗΣ: ΔΗΜΗΤΡΙΑΔΗΣ ΣΤΑΥΡΟΣ Επ. Καθηγητής ΘΕΣΣΑΛΟΝΙΚΗ 2015 ΠΕΡΙΛΗΨΗ Π ΕΡΙΛΗΨΗ Αντικείμενο της παρούσας εργασίας είναι η παιχνιδοκεντρική μάθηση και η ανάπτυξη ενός εκπαιδευτικού παιχνιδιού. Με την ανάπτυξη της τεχνολογίας στις μέρες μας, η διαδικασία της εκπαίδευσης και της μάθησης έχουν αλλάξει δραματικά. Η μάθηση δεν είναι πλέον μια κλασσική διαδικασία που στηρίζεται μόνο στα βιβλία. Η εργασία ασχολείται με την παιχνιδοκεντρική μάθηση και τη χρήση των παιχνιδιών σε αυτή τη διαδικασία, ενώ περιγράφεται και η ανάπτυξη ενός τέτοιου εκπαιδευτικού παιχνιδιού. Στο πρώτο μέρος περιγράφεται η έννοια της παιχνιδοκεντρικής μάθησης, εκείνης της διαδικασίας μάθησης που χρησιμοποιεί ως μηχανισμό το παιχνίδι. Επίσης περιγράφονται οι διάφορες κατηγορίες εκπαιδευτικών παιχνιδιών. Στο δεύτερο μέρος γίνεται αναφορά στη γλώσσα Python, το μοντέλο εκτέλεσής της και την ιστορία της. Έπειτα γίνεται αναφορά στη βιβλιοθήκη Pygame και στα εργαλεία που χρησιμοποιήθηκαν στην ανάπτυξη του παιχνιδιού. Στο τρίτο μέρος της εργασίας αναλύεται η υλοποίηση ενός εκπαιδευτικού ψηφιακού παιχνιδιού με τίτλο «Binary Droids», υλοποιημένο σε Python, με χρήση της Pygame. Το παιχνίδι έχει σκοπό την εκμάθηση μιας βασικής έννοιας της Πληροφορικής, αυτήν του δυαδικού συστήματος αρίθμησης, και της μετατροπής αριθμών από το δυαδικό σύστημα στο γνωστό σε όλους δεκαδικό. Το παιχνίδι χρησιμοποιεί επιβραβεύσεις και ποινές, όταν ο χρήστης εκτελεί τις μετατροπές των αριθμών σωστά και όταν τις εκτελεί λάθος, αντίστοιχα. Όσο ο χρήστης επιβραβεύεται για τις επιδόσεις του στο παιχνίδι, ανεβαίνει επίπεδα και συνεπώς αυξάνεται και η δυσκολία. -

Laura Tateosian Python for Arcgis Python for Arcgis
Laura Tateosian Python For ArcGIS Python For ArcGIS Laura Tateosian Python For ArcGIS Laura Tateosian North Carolina State University Raleigh , NC , USA ISBN 978-3-319-18397-8 ISBN 978-3-319-18398-5 (eBook) DOI 10.1007/978-3-319-18398-5 Library of Congress Control Number: 2015943490 Springer Cham Heidelberg New York Dordrecht London © Springer International Publishing Switzerland 2015 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifi cally the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfi lms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specifi c statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. Esri images are used by permission. Copyright © 2015 Esri. All rights reserved. Python is copyright the Python Software Foundation. Used by permission. PyScripter is an OpenSource software authored by Kiriakos Vlahos. -
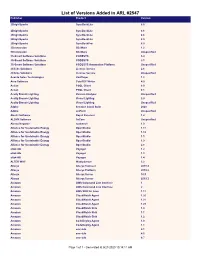
List of Versions Added in ARL #2547 Publisher Product Version
List of Versions Added in ARL #2547 Publisher Product Version 2BrightSparks SyncBackLite 8.5 2BrightSparks SyncBackLite 8.6 2BrightSparks SyncBackLite 8.8 2BrightSparks SyncBackLite 8.9 2BrightSparks SyncBackPro 5.9 3Dconnexion 3DxWare 1.2 3Dconnexion 3DxWare Unspecified 3S-Smart Software Solutions CODESYS 3.4 3S-Smart Software Solutions CODESYS 3.5 3S-Smart Software Solutions CODESYS Automation Platform Unspecified 4Clicks Solutions License Service 2.6 4Clicks Solutions License Service Unspecified Acarda Sales Technologies VoxPlayer 1.2 Acro Software CutePDF Writer 4.0 Actian PSQL Client 8.0 Actian PSQL Client 8.1 Acuity Brands Lighting Version Analyzer Unspecified Acuity Brands Lighting Visual Lighting 2.0 Acuity Brands Lighting Visual Lighting Unspecified Adobe Creative Cloud Suite 2020 Adobe JetForm Unspecified Alastri Software Rapid Reserver 1.4 ALDYN Software SvCom Unspecified Alexey Kopytov sysbench 1.0 Alliance for Sustainable Energy OpenStudio 1.11 Alliance for Sustainable Energy OpenStudio 1.12 Alliance for Sustainable Energy OpenStudio 1.5 Alliance for Sustainable Energy OpenStudio 1.9 Alliance for Sustainable Energy OpenStudio 2.8 alta4 AG Voyager 1.2 alta4 AG Voyager 1.3 alta4 AG Voyager 1.4 ALTER WAY WampServer 3.2 Alteryx Alteryx Connect 2019.4 Alteryx Alteryx Platform 2019.2 Alteryx Alteryx Server 10.5 Alteryx Alteryx Server 2019.3 Amazon AWS Command Line Interface 1 Amazon AWS Command Line Interface 2 Amazon AWS SDK for Java 1.11 Amazon CloudWatch Agent 1.20 Amazon CloudWatch Agent 1.21 Amazon CloudWatch Agent 1.23 Amazon -

Physical Sciences
Current classroom software 2018-19 Physical Sciences These applications are available in the Physical Sciences folder on all PCs in teaching labs and ad-hoc areas unless otherwise stated. Please refer any problems you may have running these applications to the Service Desk ([email protected]). • Engineering • Geosciences • Natural and Computing Sciences Engineering Folder Name Software Comments Engineering ABAQUS 2017 ANSYS 18.1 Arduino BBC BASIC for Windows Bloodshed Dev C++ CES EduPack 2018 Cygwin -X Drillbench Emacs Flexcom - HASP Fritzing KAPPA Landmark LTspice MathCAD Matlab 2018 Orcaflex Petrel 2017 Petroleum Experts v10 PipeSim Design Spark PCB v8.1 SAP 2000 v20 Rhinoceros Schlumberger SL Solidworks 2018 SprutCAM11 tNavigator Visio 2017 Certain Locations Visual Studio UniSim Design R430 STAAD GeoSciences Folder Name Software Comments Archaeology ArcGIS Bonn Archaeology Software Basp Past CastCor LuminCor PerCor Posthole RadCor Slides Winbasp MapViewer Harris Matrix Program ArchEd Luminescence Analyst MorphoJ OxCal Stratify 1.5 Gimp 2.10 inkscape yEd Graph Editor Tools for Quantitative Documentation Archaeology TFQA Programs Geography and Environment Canvis 2.3 Coastal Ecology Coastal Habitat Restoration Coastal Engineering Coast Ranger Inverbervie Rosehearty SANDS Stonehaven Digital Elevation Models Micro DEM Digital Mapping and Admiralty RYA Chartplotter Cartology Training Atlas of Switzerland Map Design Mapviewer 6 Maptime RYA Plotter Digital Tutorial Surfer 9 Geographical Information ArcExplorer 2.0 Systems (GIS) ArcGIS -

Phycore-MPC5554
QuickStart Instructions PowerPC Kit phyCORE-MPC5554 Using iSYSTEM winIDEA for PowerPC Development Tool Chain Note: The PHYTEC Tool-CD includes the electronic version of the phyCORE-MPC5554 English Hardware Manual Edition: January 2013 A product of a PHYTEC Technology Holding company phyCORE-MPC5554 QuickStart Instructions In this manual are descriptions for copyrighted products that are not explicitly indicated as such. The absence of the trademark () and copyright () symbols does not imply that a product is not protected. Additionally, registered patents and trademarks are similarly not expressly indicated in this manual. The information in this document has been carefully checked and is believed to be entirely reliable. However, PHYTEC Messtechnik GmbH assumes no responsibility for any inaccuracies. PHYTEC Messtechnik GmbH neither gives any guarantee nor accepts any liability whatsoever for consequential damages resulting from the use of this manual or its associated product. PHYTEC Messtechnik GmbH reserves the right to alter the information contained herein without prior notification and accepts no responsibility for any damages which might result. Additionally, PHYTEC Messtechnik GmbH offers no guarantee nor accepts any liability for damages arising from the improper usage or improper installation of the hardware or software. PHYTEC Messtechnik GmbH further reserves the right to alter the layout and/or design of the hardware without prior notification and accepts no liability for doing so. Copyright 2013 PHYTEC Messtechnik GmbH, D-55129 Mainz. Rights - including those of translation, reprint, broadcast, photomechanical or similar reproduction and storage or processing in computer systems, in whole or in part - are reserved. No reproduction may occur without the express written consent from PHYTEC Messtechnik GmbH. -

Programming Shadows
Programming Shadows Computer programming in the context of the Sundial Simon Wheaton-Smith FRI, MBCS, CITP Phoenix, AZ 1 ILLUSTRATING TIME’S SHADOW Programming Shadows by Simon Wheaton-Smith my business card in 1970 ISBN 978-0-9960026-2-2 Library of Congress Control Number: 2014904841 Simon Wheaton-Smith www.illustratingshadows.com [email protected] (c) 2004-2020 Simon Wheaton-Smith All rights reserved. February 14, 2017 April 1, 2020 2 THE ILLUSTRATING SHADOWS COLLECTION Illustrating Shadows provides several books or booklets:- Simple Shadows Build a horizontal dial for your location. Appropriate theory. Cubic Shadows Introducing a cube dial for your location. Appropriate theory. Cutting Shadows Paper cutouts for you to make sundials with. Illustrating Times Shadow the big book Illustrating Times Shadow ~ Some 400 pages covering almost every aspect of dialing. Includes a short appendix. Appendices Illustrating Times Shadow ~ The Appendices ~ Some 180 pages of optional detailed appendix material. Supplement Supplemental Shadows ~ Material in the form of a series of articles, covers more on the kinds of time, declination confusion, other proofs for the vertical decliner, Saxon, scratch, and mass dials, Islamic prayer times (asr), dial furniture, and so on! Programming Shadows A book discussing many programming languages, their systems and how to get them, many being free, and techniques for graphical depictions. This covers the modern languages, going back into the mists of time. Legacy languages include ALGOL, FORTRAN, the IBM 1401 Autocoder and SPS, the IBM 360 assembler, and Illustrating Shadows provides simulators for them, including the source code. Then C, PASCAL, BASIC, JAVA, Python, and the Lazarus system, as well as Octave, Euler, and Scilab. -

Python Web Aplikacija
Python web aplikacija Rebrović, Ivona Undergraduate thesis / Završni rad 2015 Degree Grantor / Ustanova koja je dodijelila akademski / stručni stupanj: Polytechnic of Međimurje in Čakovec / Međimursko veleučilište u Čakovcu Permanent link / Trajna poveznica: https://urn.nsk.hr/urn:nbn:hr:110:257734 Rights / Prava: In copyright Download date / Datum preuzimanja: 2021-10-01 Repository / Repozitorij: Polytechnic of Međimurje in Čakovec Repository - Polytechnic of Međimurje Undergraduate and Graduate Theses Repository MEĐIMURSKO VELEUČILIŠTE U ČAKOVCU RAČUNARSTVO IVONA REBROVIĆ PYTHON WEB APLIKACIJA ZAVRŠNI RAD ČAKOVEC, 2015. MEĐIMURSKO VELEUČILIŠTE U ČAKOVCU RAČUNARSTVO IVONA REBROVIĆ PYTHON WEB APLIKACIJA PYTHON WEB APPLICATION ZAVRŠNI RAD Mentor: mr. sc. Bruno Trstenjak ČAKOVEC, 2015. Ivona Rebrović Python web aplikacija ZAHVALA Zahvalila bih se svim profesorima Međimurskog veleučilišta u Čakovcu i mentoru mr.sc. Bruni Trstenjaku na svom pruženom znanju i podršci tokom studiranja te pomoći kod izrade i realizacije ovog završnog rada. Međimursko Veleučilište u Čakovcu Ivona Rebrović Python web aplikacija SAŽETAK Cilj ovog završnog rada je prikazati karakteristike i mogućnosti Pythona te rad Python web aplikacije. Python web aplikacija rađena je u Eclipse Java EE IDE razvojnom okruženju. Korištena je verzija Luna Release 4.4.0. Eclipse nudi šest vrsta alata za Python razvojnu okolinu. U razvoju aplikacije korišten je PyDev alat te Django open-source web razvojna okolina. Django je pisan u Pythonu te koristi model - pogled - predložak ( MVT ) arhitekturu. U svom radu, Python web aplikacija upotrebom SciKit razvojnog paketa i Naive Bayes-ovog algoritma izračunava vjerojatnost uspješnosti studenta u studiranju. SciKit razvojni paket sadrži biblioteku raznih klasa iz područja strojnog učenja i Data mininga. Klase omogućuju implementaciju raznih metoda i algoritama za klasifikaciju podataka te određivanje regresije među podacima i atributima. -

Development Software Downloads
Development software downloads New Mexico Supercomputing Challenge, Oct. 2019 Java Java Development Kit (JDK) Most widely available versions of the JDK have at least 2 sources. Below, we’ve listing Oracle-licensed JDK and GPL-licensed OpenJDK downloads. Oracle-licensed releases permit no-cost non-commercial (including educational) use, while OpenJDK-based releases are licensed under the GPL w/ classpath exception license, which permits even most commercial use at no cost. Apart from that, there is little (if any) practical difference between releases of the same version from the different sources. We’ve listed several different versions of Java here. Unfortunately, this is necessitated by the practical fact that different versions are used for different purposes. For example: If you want to take advantage of the latest features added to the Java language, you should use the latest release; currently, that’s JDK 13. If you want to use the jshell read-evaluate-print-loop (command-line interpreter) tool, you have to use a JDK 9 or higher—which, for most practical purposes, means you need to use (for now) JDK 11, JDK 12, or JDK 13. If you want to use a JDK that has an expectation of long-term support (LTS), your options (at least until 2021) are limited to JDK 8 and JDK 11. If you want to write Android apps, you must use JDK 8. If you want to use a single JDK for writing Java programs and for running NetLogo, you must use JDK 8. If you want to write and run Java code on a flash drive -based environment, and if you don’t want to do the extra work required to setup a suitably-featured Linux environment on a flash drive, you’re limited to using portableApps.com (which is Windows-only) with JDK 8 or JDK 12. -

Towards Left Duff S Mdbg Holt Winters Gai Incl Tax Drupal Fapi Icici
jimportneoneo_clienterrorentitynotfoundrelatedtonoeneo_j_sdn neo_j_traversalcyperneo_jclientpy_neo_neo_jneo_jphpgraphesrelsjshelltraverserwritebatchtransactioneventhandlerbatchinsertereverymangraphenedbgraphdatabaseserviceneo_j_communityjconfigurationjserverstartnodenotintransactionexceptionrest_graphdbneographytransactionfailureexceptionrelationshipentityneo_j_ogmsdnwrappingneoserverbootstrappergraphrepositoryneo_j_graphdbnodeentityembeddedgraphdatabaseneo_jtemplate neo_j_spatialcypher_neo_jneo_j_cyphercypher_querynoe_jcypherneo_jrestclientpy_neoallshortestpathscypher_querieslinkuriousneoclipseexecutionresultbatch_importerwebadmingraphdatabasetimetreegraphawarerelatedtoviacypherqueryrecorelationshiptypespringrestgraphdatabaseflockdbneomodelneo_j_rbshortpathpersistable withindistancegraphdbneo_jneo_j_webadminmiddle_ground_betweenanormcypher materialised handaling hinted finds_nothingbulbsbulbflowrexprorexster cayleygremlintitandborient_dbaurelius tinkerpoptitan_cassandratitan_graph_dbtitan_graphorientdbtitan rexter enough_ram arangotinkerpop_gremlinpyorientlinkset arangodb_graphfoxxodocumentarangodborientjssails_orientdborientgraphexectedbaasbox spark_javarddrddsunpersist asigned aql fetchplanoriento bsonobjectpyspark_rddrddmatrixfactorizationmodelresultiterablemlibpushdownlineage transforamtionspark_rddpairrddreducebykeymappartitionstakeorderedrowmatrixpair_rddblockmanagerlinearregressionwithsgddstreamsencouter fieldtypes spark_dataframejavarddgroupbykeyorg_apache_spark_rddlabeledpointdatabricksaggregatebykeyjavasparkcontextsaveastextfilejavapairdstreamcombinebykeysparkcontext_textfilejavadstreammappartitionswithindexupdatestatebykeyreducebykeyandwindowrepartitioning -

Python Scripting in FME
Webinar Python Scripting in FME Ken Bragg Tino Miegel Stefan Offermann Christian Dahmen European Services Software Engineer Software Engineer Consultant Manager con terra GmbH con terra GmbH con terra GmbH Safe Software Inc. Poll: About You #1 How long have you been using FME? > Never > Less than 1 year > 1-2 years > More than 3 years 2 © con terra GmbH Powering the Flow of Spatial Data 3 © con terra GmbH FME Workbench 4 © con terra GmbH Agenda What is Python? FME and Python Best Practice 5 © con terra GmbH Poll: About You #2 Do you have any experience with Python? > Yes, long time Python user > Yes, also within FME > Some > None 6 © con terra GmbH What is Python? Programming/Scripting Language Easy to learn and use, well documented Great user community Platform independent Great for GIS automatization tasks It‘s free! More details on www.python.org 7 © con terra GmbH Python Basics Variables (data-types) > String, Integer, Float, List, Dictionary, Tuple > Dynamic typing Built-In methods a=1 #integer > len(), max(), min(), … b='Hello, World!' #string Modules > Thematic-grouped extensions > e.g. math, os, numpy, zip, re IDEs > IDLE, PyWin, PyDev for Eclipse, PyScripter, … 8 © con terra GmbH Sample #1 # Sample #1 # print even numbers from 1 to 9 a = range(1,10) # list from…to [excluded] # for-loop for i in a: if i%2 == 0: # condition print 'number %i is even' %i else: print 'number %i is odd' %i Line indentation is very important in Python! 9 © con terra GmbH FME and Python Why and when should one make use of Python with FME Workbench? Want