DOCSLIB.ORG

Design Study for a Formation-Flying Nanosatellite Cluster

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Design Study for a Formation-Flying Nanosatellite Cluster 2005:147 CIV EXAMENSARBETE Design Study for a Formation-Flying Nanosatellite Cluster SARA GIDLUND MASTER OF SCIENCE PROGRAMME in Space Engineering Luleå University of Technology Department of Space Science, Kiruna 2005:147 CIV • ISSN: 1402 - 1617 • ISRN: LTU - EX - - 05/147 - - SE Design Study for a Formation- Flying Nanosatellite Cluster. Centre for Large Space Structures and Systems Inc. (CLS3) 1425 Blvd. René Lévesque W-700 Montreal, Québec H3G 1T7 Canada Abstract Nanosatellites flying in formation vastly increase the capability of small satellite missions. The approach is within reach of technology, but there are severe challenges for the subsystems. The most demanding task is to implement effective control of the satellites. There are many options for solving the high and the low level control. The propulsion system and the communication system are the subsystems that will determine the constraints on the formation that may be used, and the duration of the mission. The mission of the cluster that the Centre for Large Space Structures and Systems Inc (CLS3) intends to launch will make use of existing technologies for nanosatellites and merge them with an in-house Guidance Navigation and Control system. The project will be developed as a collaboration between companies and organizations, in North America and Europe. The objective of the initial study was to summarize the state-of-the-art for the subsystems, and to stimulate discussions with potential partners. Negotiations with launch companies were also initiated. The satellites will fly in a circular or projected circular formation. In order to calculate the orbits of the satellites, it is of great importance to understand the Hill’s equations. Even though they do not include any of the major perturbations of the orbits, these equations are widely used for design of the control loops for formation-flying constellations. Acknowledgements This thesis would not have been completed if not for the guidance of Professor Hannah Michalska and the support of Björn Graneli. She was there to guide me on location, and he has been a great support, always calm, inspirational and encouraging. Björn Söderlund and Vladislav Ganine were also a great help. Thank you both for lighting up the days when the whole world seemed to rest on my shoulders, especially Björn Söderlund who had to put up with me 24-7. Thank you Dr Milind Pimprikar for taking me on, and giving me the opportunity to become a part of this interesting project, and thank you Rozita for the help with reports and presentations while in Montreal. Also thank you Roland Magnusson, for the use of your computer when mine crashed, and for your positive everything-works-out-in-the-end attitude. Last but not least, thanks to my parents: Without your loving care and support – where would I be today? 1. Table of Contents 1. Table of Contents............................................................................................................ 1 2. Abbreviations used.......................................................................................................... 5 3. List of Figures................................................................................................................. 7 4. List of Tables .................................................................................................................. 9 5. Introduction................................................................................................................... 11 6 Introductory literature study .......................................................................................... 13 6.1 Comparative analysis of Small Satellites.................................................................................................13 6.2 Comparison of formation flight missions ................................................................................................15 7 Subsystems..................................................................................................................... 17 7.1 GNC.........................................................................................................................................................17 7.1.1 Sensors........................................................................................................................................17 7.1.1.1 GPS ..................................................................................................................................................... 17 7.1.1.2 Sun sensors.......................................................................................................................................... 17 7.1.1.3 Star tracker .......................................................................................................................................... 18 7.1.1.4 Earth-horizon sensor ........................................................................................................................... 18 7.1.1.5 Inertia sensors...................................................................................................................................... 18 7.1.2 Actuators.....................................................................................................................................18 7.1.3 Control architectures...................................................................................................................18 7.1.3.1 Centralized approach........................................................................................................................... 19 7.1.3.2 Decentralized approach ....................................................................................................................... 19 7.1.3.3 Executive controller approaches.......................................................................................................... 19 7.1.3.3.1 Intelligent agent based system..................................................................................................... 19 7.1.3.3.2 Rule-based expert system............................................................................................................ 19 7.1.3.3.3 Flocking/Market-oriented programming system......................................................................... 20 7.2 Thermal ...................................................................................................................................................20 7.2.1 Background.................................................................................................................................20 7.2.1.1 Passive Thermal Control ..................................................................................................................... 20 7.2.1.1.1 Phase Change Devices ................................................................................................................ 20 7.2.1.1.2 Thermal Control Coatings........................................................................................................... 20 7.2.1.1.3 Multi Layer Insulation (MLI)...................................................................................................... 20 7.2.1.1.4 Thermal Doublers ....................................................................................................................... 20 7.2.1.2 Active Thermal Control....................................................................................................................... 21 7.2.1.2.1 Smart thermal coatings................................................................................................................ 21 7.2.1.2.2 Heat Pipe..................................................................................................................................... 21 7.2.1.2.3 Louvers ....................................................................................................................................... 21 7.2.1.2.4 Second-Surface Mirror................................................................................................................ 22 7.2.1.2.5 Electrical Heater.......................................................................................................................... 22 7.2.2 Design .........................................................................................................................................22 7.2.3 Specifications..............................................................................................................................23 7.2.3.1 From the launching company .............................................................................................................. 23 7.2.3.2 From the orbit...................................................................................................................................... 23 7.3 Structure & Separation ............................................................................................................................24 7.3.1 Specifications..............................................................................................................................24 7.3.2 Design .........................................................................................................................................25 7.4 Power.......................................................................................................................................................25 7.4.1 Solar Cells...................................................................................................................................25
Load more

Recommended publications
  • Sixty Years of Australia in Space
    Journal & Proceedings of the Royal Society of New South Wales, vol. 153, part 1, 2020, pp. 46–57. ISSN 0035-9173/20/010046-12 Sixty years of Australia in space Kerrie Dougherty Space Humanities Department, International Space University, Strasbourg, France Email: [email protected] Abstract Australia’s involvement in space activities commenced in 1957, at the beginning of the Space Age, with space tracking and sounding rocket launches at Woomera. By 1960, Australia was considered one of the leading space-active nations and in 1967 became one of the earliest countries to launch its own satellite. Yet by 1980, Australia’s space prominence had dwindled, with the country lacking both a national space agency and a coherent national space policy. Despite attempts in the latter part of the 1980s to develop an Australian space industry, the lack of a coherent and consistent national space policy and an effective co-ordinating body, left Australia constantly “punching below its weight” in global space activities until the Twenty First Century. This paper will briefly examine the often-contradictory history of Australian space activities from 1957 to the announcement of the Australian Space Agency in 2017, providing background and context for the later papers in this issue. Introduction Launchpad: the Woomera or 60,000 years the Indigenous people of Rocket Range FAustralia have looked to the sky, using “If the Woomera Range did not already exist, the stars to determine their location, find the proposal that Australia should engage in their way across the land and mark the a program of civil space research would be passage of the seasons and the best times unrealistic”.
    [Show full text]
  • A Software Package to Support Mission Analysis and Orbital Mechanics Calculations
    A Software Package to Support Mission Analysis and Orbital Mechanics Calculations Jorge Tiago Melo Barbosa da Silva e Vila Thesis to obtain the Master of Science Degree in Aerospace Engineering Supervisor: Prof. Paulo Jorge Soares Gil Examination Committee Chairperson: Prof. João Manuel Lage de Miranda Lemos Supervisor: Prof. Paulo Jorge Soares Gil Members of the Committee: Prof. Bertinho Manuel D'Andrade da Costa July of 2015 Dedicated to the loving memory of my grandfather Joaquim Barbosa, whom I shall always remember. Acknowledgements Firstly, I would like to express my gratitude to my supervisor Prof. Paulo Gil for the ideas, remarks, comments, and many engaging conversations which not only saw me through the learning process of this thesis, but also helped me personally. I want to thank Dr. Carlos del Burgo Díaz for the confidence shown in future applications of the software and the help provided with the star map alignment. I want to acknowledge Patrice-Emmanuel Schmitz, from the Open Source Observatory and Repository, for his legal opinions regarding the EUPL licensing. Furthermore, I want to thank Pavel Holoborodko for the excellent MPFR C++ interface class and the professionalism, sympathy, and cooperation displayed while resolving licensing issues. I would also like to thank my parents for the care and interest shown throughout the years in my education, and for the support given in pursuing the interests which led me here. Lastly, I want to express my deepest gratitude to Ana Morais for the love, patience, and continuous support during the development of this thesis. Without you none of this would have been possible.
    [Show full text]
  • Aerospace, Defense, and Government Services Mergers & Acquisitions
    Aerospace, Defense, and Government Services Mergers & Acquisitions (January 1993 - April 2020) Huntington BAE Spirit Booz Allen L3Harris Precision Rolls- Airbus Boeing CACI Perspecta General Dynamics GE Honeywell Leidos SAIC Leonardo Technologies Lockheed Martin Ingalls Northrop Grumman Castparts Safran Textron Thales Raytheon Technologies Systems Aerosystems Hamilton Industries Royce Airborne tactical DHPC Technologies L3Harris airport Kopter Group PFW Aerospace to Aviolinx Raytheon Unisys Federal Airport security Hydroid radio business to Hutchinson airborne tactical security businesses Vector Launch Otis & Carrier businesses BAE Systems Dynetics businesses to Leidos Controls & Data Premiair Aviation radios business Fiber Materials Maintenance to Shareholders Linndustries Services to Valsef United Raytheon MTM Robotics Next Century Leidos Health to Distributed Energy GERAC test lab and Technologies Inventory Locator Service to Shielding Specialities Jet Aviation Vienna PK AirFinance to ettain group Night Vision business Solutions business to TRC Base2 Solutions engineering to Sopemea 2 Alestis Aerospace to CAMP Systems International Hamble aerostructure to Elbit Systems Stormscope product eAircraft to Belcan 2 GDI Simulation to MBDA Deep3 Software Apollo and Athene Collins Psibernetix ElectroMechanical Aciturri Aeronautica business to Aernnova IMX Medical line to TransDigm J&L Fiber Services to 0 Knight Point Aerospace TruTrak Flight Systems ElectroMechanical Systems to Safran 0 Pristmatic Solutions Next Generation 911 to Management
    [Show full text]
  • INTERNATIONAL Call for Papers & Registration of Interest
    ORGANIZED BY: HOSTED BY: st 71 INTERNATIONAL ASTRONAUTICAL CONGRESS 12–16 October 2020 | Dubai, United Arab Emirates Call for Papers & Registration of Interest Second Announcement SUPPORTED BY: Inspire, Innovate & Discover for the Benefit of Humankind IAC2020.ORG Contents 1. Message from the International Astronautical Federation (IAF) 2 2. Message from the Local Organizing Committee 2 3. Message from the IPC Co-Chairs 3 4. Messages from the Partner Organizations 4 5. International Astronautical Federation (IAF) 5 6. International Academy of Astronautics (IAA) 10 7. International Institute of Space Law (IISL) 11 8. Message from the IAF Vice President for Technical Activities 12 9. IAC 2020 Technical Sessions Deadlines Calendar 49 10. Preliminary IAC 2020 at a Glance 50 11. Instructions to Authors 51 Connecting @ll Space People 12. Space in the United Arab Emirates 52 www.iafastro.org IAF Alliance Programme Partners 2019 1 71st IAC International Astronautical Congress 12–16 October 2020, Dubai 1. Message from the International Astronautical Federation (IAF) 3. Message from the International Programme Committee (IPC) Greetings! Co-Chairs It is our great pleasure to invite you to the 71st International Astronautical Congress (IAC) to take place in Dubai, United Arab Emirates On behalf of the International Programme Committee, it is a great pleasure to invite you to submit an abstract for the 71st International from 12 – 16 October 2020. Astronautical Congress IAC 2020 that will be held in Dubai, United Arab Emirates. The IAC is an initiative to bring scientists, practitioners, engineers and leaders of space industry and agencies together in a single platform to discuss recent research breakthroughs, technical For the very first time, the IAC will open its doors to the global space community in the United Arab Emirates, the first Arab country to advances, existing opportunities and emerging space technologies.
    [Show full text]
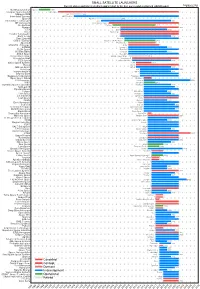
  • Small Satellite Launchers
    SMALL SATELLITE LAUNCHERS NewSpace Index 2020/04/20 Current status and time from development start to the first successful or planned orbital launch NEWSPACE.IM Northrop Grumman Pegasus 1990 Scorpius Space Launch Demi-Sprite ? Makeyev OKB Shtil 1998 Interorbital Systems NEPTUNE N1 ? SpaceX Falcon 1e 2008 Interstellar Technologies Zero 2021 MT Aerospace MTA, WARR, Daneo ? Rocket Lab Electron 2017 Nammo North Star 2020 CTA VLM 2020 Acrux Montenegro ? Frontier Astronautics ? ? Earth to Sky ? 2021 Zero 2 Infinity Bloostar ? CASIC / ExPace Kuaizhou-1A (Fei Tian 1) 2017 SpaceLS Prometheus-1 ? MISHAAL Aerospace M-OV ? CONAE Tronador II 2020 TLON Space Aventura I ? Rocketcrafters Intrepid-1 2020 ARCA Space Haas 2CA ? Aerojet Rocketdyne SPARK / Super Strypi 2015 Generation Orbit GoLauncher 2 ? PLD Space Miura 5 (Arion 2) 2021 Swiss Space Systems SOAR 2018 Heliaq ALV-2 ? Gilmour Space Eris-S 2021 Roketsan UFS 2023 Independence-X DNLV 2021 Beyond Earth ? ? Bagaveev Corporation Bagaveev ? Open Space Orbital Neutrino I ? LIA Aerospace Procyon 2026 JAXA SS-520-4 2017 Swedish Space Corporation Rainbow 2021 SpinLaunch ? 2022 Pipeline2Space ? ? Perigee Blue Whale 2020 Link Space New Line 1 2021 Lin Industrial Taymyr-1A ? Leaf Space Primo ? Firefly 2020 Exos Aerospace Jaguar ? Cubecab Cab-3A 2022 Celestia Aerospace Space Arrow CM ? bluShift Aerospace Red Dwarf 2022 Black Arrow Black Arrow 2 ? Tranquility Aerospace Devon Two ? Masterra Space MINSAT-2000 2021 LEO Launcher & Logistics ? ? ISRO SSLV (PSLV Light) 2020 Wagner Industries Konshu ? VSAT ? ? VALT
    [Show full text]
  • 1 James Webb Space Telescope Initial Mid-Course Correction Monte Carlo Implementation Using Task Parallelism Jeremy Petersen
    James Webb Space Telescope Initial Mid-Course Correction Monte Carlo Implementation using Task Parallelism Jeremy Petersen(1), Jason Tichy(2), Geoffrey Wawrzyniak(3), and Karen Richon(4) (1,2,3)a.i. solutions, Inc., 10001 Derekwood Lane, Lanham, MD 20706, 301-306-1756, [email protected]. (4)Code 595.0, NASA Goddard Space Flight Center, 8800 Greenbelt Road, Greenbelt MD, 20771. 301-286-8845, [email protected]. The James Webb Space Telescope will be launched into a highly elliptical orbit that does not possess sufficient energy to achieve a proper Sun-Earth/Moon L2 libration point orbit. Three mid-course correction (MCC) maneuvers are planned to rectify the energy deficit: MCC-1a, MCC-1b, and MCC-2. To validate the propellant budget and trajectory design methods, a set of Monte Carlo analyses that incorporate MCC maneuver modeling and execution are employed. The first analysis focuses on the effects of launch vehicle injection errors on the magnitude of MCC-1a. The second on the spread of potential V based on the performance of the propulsion system as applied to all three MCC maneuvers. The final highlights the slight, but notable, contribution of the attitude thrusters during each MCC maneuver. Given the possible variations in these three scenarios, the trajectory design methods are determined to be robust to errors in the modeling of the flight system. Keywords: James Webb Space Telescope, Task Parallelism, Monte Carlo, Mid-Course Correction, Libration Point Orbit 1. Introduction The James Webb Space Telescope (JWST) is the scientific successor of the Hubble Space Telescope and the Spitzer Space Telescope.
    [Show full text]
  • NATIONAL ACADEMIES of SCIENCES and ENGINEERING NATIONAL RESEARCH COUNCIL of the UNITED STATES of AMERICA
    NATIONAL ACADEMIES OF SCIENCES AND ENGINEERING NATIONAL RESEARCH COUNCIL of the UNITED STATES OF AMERICA UNITED STATES NATIONAL COMMITTEE International Union of Radio Science National Radio Science Meeting 4-8 January 2000 Sponsored by USNC/URSI University of Colorado Boulder, Colorado U.S.A. United States National Committee INTERNATIONAL UNION OF RADIO SCIENCE PROGRAM AND ABSTRACTS National Radio Science Meeting 4-8 January 2000 Sponsored by USNC/URSI NOTE: Programs and Abstracts of the USNC/URSI Meetings are available from: USNC/URSI National Academy of Sciences 2101 Constitution Avenue, N.W. Washington, DC 20418 at $5 for 1983-1999 meetings. The full papers are not published in any collected format; requests for them should be addressed to the authors who may have them published on their own initiative. Please note that these meetings are national. They are not organized by the International Union, nor are the programs available from the International Secretariat. ii MEMBERSHIP United States National Committee INTERNATIONAL UNION OF RADIO SCIENCE Chair: Gary Brown* Secretary & Chair-Elect: Umran S. !nan* Immediate Past Chair: Susan K. Avery* Members Representing Societies, Groups, and Institutes: American Astronomical Society Thomas G. Phillips American Geophysical Union Donald T. Farley American Meteorological Society vacant IEEE Antennas and Propagation Society Linda P.B. Katehi IEEE Geosciences and Remote Sensing Society Roger Lang IEEE Microwave Theory and Techniques Society Arthur A. Oliner Members-at-Large: Amalia Barrios J. Richard Fisher Melinda Picket-May Ronald Pogorzelski W. Ross Stone Richard Ziolkowski Chairs of the USNC/URSI Commissions: Commission A Moto Kanda Commission B Piergiorgio L. E. Uslenghi Commission C Alfred 0.
    [Show full text]
  • Progress Towards Fedsat 2001 A'stralian Space Odyssey
    SCC99-IX-6 Progress Towards FedSat 2001 A’stralian Space Odyssey Stephen Russell and Mirek Vesely Cooperative Research Centre for Satellite Systems, VIPAC Engineers and Scientists Ltd 21 King William St, Kent Town, South Australia, 5067 email: [email protected] ph. +618 8362 5445 fax. +618 8362 0793 Chris Graham Cooperative Research Centre for Satellite Systems CSIRO Telecommunications and Industrial Physics GPO Box 1483, Canberra ACT 2601, Australia email: [email protected] ph. +612 6216 7285 fax +612 6216 7272 and Mike Petkovic Cooperative Research Centre for Satellite Systems, Auspace Ltd, PO Box 17, Mitchell ACT 2911, Australia email: [email protected] ph. +612 6242 2611 fax +612 6241 6664 Abstract. In mid-1997, the Australian Government approved the setting up of a Cooperative Research Centre for Satellite Systems (CRCSS) to promote Australian space research. A key outcome of the research activities is intended to be the launching of a research satellite - FedSat- by the year 2001, the centenary year of Australian Federation. This will be the first Australian built satellite since 1970, and vital a step towards Australia's re- entry into the satellite business. This talk describes the aims of the FedSat mission; the design of the overall system; and provides up-to-date details of progress towards project completion. Neither the options of a turn-key contract, nor of Introduction building the whole system from scratch, have The FedSat satellite is, like its earlier sisters been taken. Instead, the CRCSS has opted to WRESAT and OSCAR V, a micro-satellite. take the middle road – buying a platform from However, with a mass of only 58 kilograms, she an experienced provider, with accompanying is packed with a selection of scientific payloads technology transfer, and building, assembling that are unusually complex for a nation stepping and testing the system themselves.
    [Show full text]
  • Redalyc.Status and Trends of Smallsats and Their Launch Vehicles
    Journal of Aerospace Technology and Management ISSN: 1984-9648 [email protected] Instituto de Aeronáutica e Espaço Brasil Wekerle, Timo; Bezerra Pessoa Filho, José; Vergueiro Loures da Costa, Luís Eduardo; Gonzaga Trabasso, Luís Status and Trends of Smallsats and Their Launch Vehicles — An Up-to-date Review Journal of Aerospace Technology and Management, vol. 9, núm. 3, julio-septiembre, 2017, pp. 269-286 Instituto de Aeronáutica e Espaço São Paulo, Brasil Available in: http://www.redalyc.org/articulo.oa?id=309452133001 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative doi: 10.5028/jatm.v9i3.853 Status and Trends of Smallsats and Their Launch Vehicles — An Up-to-date Review Timo Wekerle1, José Bezerra Pessoa Filho2, Luís Eduardo Vergueiro Loures da Costa1, Luís Gonzaga Trabasso1 ABSTRACT: This paper presents an analysis of the scenario of small satellites and its correspondent launch vehicles. The INTRODUCTION miniaturization of electronics, together with reliability and performance increase as well as reduction of cost, have During the past 30 years, electronic devices have experienced allowed the use of commercials-off-the-shelf in the space industry, fostering the Smallsat use. An analysis of the enormous advancements in terms of performance, reliability and launched Smallsats during the last 20 years is accomplished lower prices. In the mid-80s, a USD 36 million supercomputer and the main factors for the Smallsat (r)evolution, outlined.
    [Show full text]
  • Commercial Space Transportation Year in Review
    Associate Administrator for Commercial Space Transportation (AST) January 2001 COMMERCIAL SPACE TRANSPORTATION: 2000 YEAR IN REVIEW Cover Photo Credits (from left): International Launch Services (2000). Image is of the Atlas 3A launch on May 24, 2000, from Cape Canaveral Air Force Station. It successfully orbited the Eutelsat W4 communications satellite for Eutelsat. Boeing Corporation (1999). Image is of the Delta 2 7420 launch on July 10, 1999, Cape Canaveral Air Force Station. It successfully orbited four Globalstar communications satellites for Globalstar, Inc. Orbital Sciences Corp. (1997). Image is of the Pegasus XL that launched August 1, 1997 and deployed the Orbview 2 (Seastar) remote sensing satellite. Sea Launch (1999). Image is of the inaugural Zenit 3SL launch on March 27, 1999, from the Odyssey Sea Launch Platform. 2000 YEAR IN REVIEW INTRODUCTION INTRODUCTION In 2000, there were ten commercial launches 3A vehicle, which deployed a communications licensed by the Federal Aviation Administration spacecraft for Eutelsat. (FAA) for revenue that totaled about $625 million. This total represents seven launches Several new commercial space applications from U.S. ranges for commercial and contributed to the worldwide commercial launch government customers plus three launches by the total. Three Proton rockets deployed satellites multinational Sea Launch venture. for Sirius Satellite Radio, a company that will offer direct radio broadcast services to the United Overall, 35 worldwide commercial launches States. Three Soyuz vehicles carried cargo and a occurred in 2000. This number is slightly less cosmonaut crew to the Mir space station with than prior years (39 in 1999 and 41 in 1998). private financing from MirCorp, a company that However, the U.S.
    [Show full text]
  • Debris Mitigation, Assembly, Integration, and Test, in the Context of the Istsat-1 Project
    Debris Mitigation, Assembly, Integration, and Test, in the context of the ISTsat-1 project Paulo Luís Granja Macedo Thesis to obtain the Master of Science Degree in Aerospace Engineering Supervisors: Prof. Paulo Jorge Soares Gil Prof. Agostinho Rui Alves da Fonseca Examination Committee Chairperson: Prof. José Fernando Alves da Silva Supervisor: Prof. Paulo Jorge Soares Gil Member of the Committee: Prof. Elsa Maria Pires Henriques November 2018 ii Dedicado ao meu Pai, Mae˜ e Irma˜ iii iv Acknowledgments I want to thank my supervisors, Professor Paulo Gil and Professor Agostinho Fonseca, for guiding me thorough the project. I also want to thank the ISTsat-1 team members, both professors and students, for giving me the opportunity to be part of such a great project and for the availability they had for my questions. The project would not happen if we did not have the University help and the ESA initiative Fly Your Satellite. I want to thank both organizations, that provided and will keep providing financial support, development rooms, test facilities and expertise in Space related matters. I want to thank all the other people that helped me through this phase, my fiends and girlfriend, thank you. Tambem´ quero agradecer aos meus pais e irma,˜ que me ajudaram em tudo o que foi preciso para chegar a este dia, sem eles nao˜ seria poss´ıvel. Obrigado. v vi Resumo O ISTsat-1 e´ um CubeSat desenvolvido por estudantes e professores do Instituto Superior Tecnico´ (IST), com a ajuda de um programa da ESA chamado Fly Your Satellite (FYS). O objectivo principal e´ educar estudantes em cienciaˆ e tecnologia espacial.
    [Show full text]
  • <> CRONOLOGIA DE LOS SATÉLITES ARTIFICIALES DE LA
    1 SATELITES ARTIFICIALES. Capítulo 5º Subcap. 10 <> CRONOLOGIA DE LOS SATÉLITES ARTIFICIALES DE LA TIERRA. Esta es una relación cronológica de todos los lanzamientos de satélites artificiales de nuestro planeta, con independencia de su éxito o fracaso, tanto en el disparo como en órbita. Significa pues que muchos de ellos no han alcanzado el espacio y fueron destruidos. Se señala en primer lugar (a la izquierda) su nombre, seguido de la fecha del lanzamiento, el país al que pertenece el satélite (que puede ser otro distinto al que lo lanza) y el tipo de satélite; este último aspecto podría no corresponderse en exactitud dado que algunos son de finalidad múltiple. En los lanzamientos múltiples, cada satélite figura separado (salvo en los casos de fracaso, en que no llegan a separarse) pero naturalmente en la misma fecha y juntos. NO ESTÁN incluidos los llevados en vuelos tripulados, si bien se citan en el programa de satélites correspondiente y en el capítulo de “Cronología general de lanzamientos”. .SATÉLITE Fecha País Tipo SPUTNIK F1 15.05.1957 URSS Experimental o tecnológico SPUTNIK F2 21.08.1957 URSS Experimental o tecnológico SPUTNIK 01 04.10.1957 URSS Experimental o tecnológico SPUTNIK 02 03.11.1957 URSS Científico VANGUARD-1A 06.12.1957 USA Experimental o tecnológico EXPLORER 01 31.01.1958 USA Científico VANGUARD-1B 05.02.1958 USA Experimental o tecnológico EXPLORER 02 05.03.1958 USA Científico VANGUARD-1 17.03.1958 USA Experimental o tecnológico EXPLORER 03 26.03.1958 USA Científico SPUTNIK D1 27.04.1958 URSS Geodésico VANGUARD-2A
    [Show full text]