Paper Title [Font: Times New Roman, Size:20]
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Belgaum), Karnataka, India
Public Disclosure Authorized GOVERNMENT OF KARNATAKA Karnataka Urban Water Supply Modernization Project (KUWSMP) Public Disclosure Authorized ENVIRONMENTAL AND SOCIAL ASSESSMENT (ESA) OF CONTINUOUS WATER SUPPLY PROJECT IN BELAGAVI (BELGAUM), KARNATAKA, INDIA Public Disclosure Authorized DRAFT FINAL REPORT 2014 Public Disclosure Authorized Karnataka Urban Infrastructure Development Finance Corporation (KUIDFC) KUIDFC Abbreviations AE Assistant Engineer AEE Assistant Executive Engineer CMC City Municipal Corporation CPCB Central Pollution Control Board CPHEEO Central Public Health & Environmental Engineering Organisation DoEE Department of Ecology & Environment (DoEE) DPR Detailed Project Report DRIP Dam Rehabilitation and Improvement Project EA Environmental Assessment EAC Expert Appraisal Committee EC Empowered Committee EIA Environmental Impact Assessment EMP Environmental Management Plan EP Environment Protection ESMP Environmental and Social Management Plan FGD Focused Group Discussions GLSR Ground Level Storage Reservoir GoI Government of India GoK Government of Karnataka JE Junior Engineer Km Kilometer KSPCB Karnataka State Pollution control Board KUIDFC Karnataka Urban Infrastructure Development Finance Corporation KUWASIP Karnataka Urban Water Sector Improvement Project KUWSSDB Karnataka Urban Water Supply Sewerage and Drainage Board KUWSMP Karnataka Urban Water Supply Modernization Project LPCD Litres per capita per day mg/l Milligrams per liter MoEF Ministry of Environment & Forests NH National Highway NRRP National Rehabilitation -

Village Code NAME of STATE, DISTRICTS, SUB-DISTTS
State District Sub-District Village Code NAME OF STATE, DISTRICTS, SUB-DISTTS. & VILLAGES Code Code Code 2001 29 00 0000 00000000 KARNATAKA 29 01 0000 00000000 Belgaum 29 01 0001 00000000 Chikodi 29 01 0001 00000100 Hadnal 29 01 0001 00000200 Sulagaon 29 01 0001 00000300 Mattiwade 29 01 0001 00000400 Bhatnaganur 29 01 0001 00000500 Kurli 29 01 0001 00000600 Appachiwadi 29 01 0001 00000700 Koganoli 29 01 0001 00000800 Hanabarawadi 29 01 0001 00000900 Hanchinal (K.S.) 29 01 0001 00001000 Benadi 29 01 0001 00001100 Bolewadi 29 01 0001 00001200 Akkol 29 01 0001 00001300 Padlihal 29 01 0001 00001400 Lakhanapur 29 01 0001 00001500 Jatrat 29 01 0001 00001600 Adi 29 01 0001 00001700 Bhivashi 29 01 0001 00001800 Naganur 29 01 0001 00001900 Yamagarni 29 01 0001 00002000 Soundalga 29 01 0001 00002100 Budihal 29 01 0001 00002200 Kodni 29 01 0001 00002300 Gayakanawadi 29 01 0001 00002400 Shirguppi 29 01 0001 00002500 Pangeri (B) 29 01 0001 00002600 Budulmukh 29 01 0001 00002700 Shendur 29 01 0001 00002800 Gondikuppi 29 01 0001 00002900 Yarnal 29 01 0001 00003000 Nippani (Rural) 29 01 0001 00003100 Amalzari 29 01 0001 00003200 Gavan 29 01 0001 00003300 Tavadi 29 01 0001 00003400 Manakapur 29 01 0001 00003500 Kasanal 29 01 0001 00003600 Donewadi 29 01 0001 00003700 Boragaon 29 01 0001 00003800 Boragaonwadi 29 01 0001 00003900 Sadalaga (Rural) 29 01 0001 00004000 Janwad 29 01 0001 00004100 Shiradwad 29 01 0001 00004200 Karadaga 29 01 0001 00004300 Barwad 29 01 0001 00004400 Mangur 29 01 0001 00004500 Kunnur 29 01 0001 00004600 Gajabarwadi 29 01 0001 00004700 Shivapurawadi 29 01 0001 00004800 Bhoj 29 01 0001 00004900 Hunnaragi Page 1 of 1117 State District Sub-District Village Code NAME OF STATE, DISTRICTS, SUB-DISTTS. -

SONATA SOFTWARE LTD Dividend UNPAID REGISTER for the YEAR FNL
SONATA SOFTWARE LTD Dividend UNPAID REGISTER FOR THE YEAR FNL. DIV. 2018-2019 AS ON 31.12.2019 Sno Dpid Folio/Clid Name Warrant No Total_Shares Net Amount Address-1 Address-2 Address-3 Address-4 Pincode 1 SON013776 LALITENDU KESHARI BARIK 2800003 300 2400.00 1/M ARUNDOYA NAGAR CUTTACK BARODA 0 2 SOP001174 MAHATHI S S 2800005 1150 9200.00 1649 SILVER TREE LANE SIMI VALLEY CA 93065 3 IN301918 10011298 RANA CHAWLA 2800011 2000 16000.00 C 65 PANCHSHEEL ENCLAVE NEW DELHI 110017 4 SON007586 MADHU DHYANI 2800013 1000 8000.00 C/O ARUN KANDPAL 1696 LAXMI BAI NAGAR NEW DELHI 110023 5 SON011742 ARUDRA NAMARA TRADING PVT LTD 2800014 5000 40000.00 D-276 DEFENCE COLONY NEW DELHI 110024 6 SOP000394 ROBANJEET SINGH SONI 2800015 4600 36800.00 HOUSE NO 1/9120 STREET-4 WEST KOTHAS NAGAR SHAHDARA DELHI 110032 7 SON008004 ARUNA OBEROI 2800022 1000 8000.00 279 KAILASH HILLS EAST OF KAILASH NEW DELHI 110065 8 SON001393 CHINTALAPATI SURYANARAYANA RAJU 2800036 1000 8000.00 B-304 SUN-N-SEA APARTMENTS EAST POINT COLONY VISAKHAPATNAM NEAR TARAKARAMA PARK ANDHRA PRADESH 530017 9 IN301774 10057077 Bhupender Singh Beniwal 2800038 400 3200.00 MF/A-1 Old Campus CCS Hau Hisar 125004 10 SON005473 SURINDER KUMAR 2800043 1000 8000.00 388 SECTOR 11 AND 12 PHASE II HUDA PANIPAT 132103 11 IN301330 17924857 JANAK RAJ 2800047 300 2400.00 H NO 104 LAWRENCE ROAD AMRITSAR, AMRITSAR 143001 12 SON005492 RACHNA IYER 2800049 1000 8000.00 C/O DR CHOPRA 1712 SECTOR 16 FARIDABAD HARYANA 151203 13 IN301774 12008948 MOHD RAMZAN SOFI 2800055 194 1552.00 MATTAN ANANTNAG 192125 14 120447 0005178141 -

Government of Karnataka RURAL O/O Commissioner
Government of Karnataka RURAL O/o Commissioner for Public Instruction, Nrupatunga Road, Bangalore - 560001 Provisional Habitation wise Neighbourhood Schools - 2016 ( RURAL ) Habitation Name School Code Management type Lowest Highest class Entry class class Habitation code / Ward code School Name Medium Sl.No. District : Belgaum Block : BAILHONGAL Habitation : Anigol---29010200101 29010200101 29010200101 Govt. 1 7 Class 1 Anigol K.H.P.S. ANIGOL 05 - Kannada 1 Habitation : Amatur---29010200201 29010200201 29010200201 Govt. 1 7 Class 1 Amatur K.H.P.S. AMATUR 05 - Kannada 2 Habitation : Amarapur---29010200301 29010200301 29010200301 Govt. 1 5 Class 1 Amarapur K.L.P.S. AMARAPUR 05 - Kannada 3 Habitation : Avaradi---29010200401 29010200401 29010200401 Govt. 1 8 Class 1 Avaradi K.H.P.S. AVARADI 05 - Kannada 4 Habitation : Ambadagatti---29010200501 29010200501 29010200501 Govt. 1 7 Class 1 Ambadagatti K.H.P.S. AMBADAGATTI 05 - Kannada 5 29010200501 29010200502 Govt. 1 5 Class 1 Ambadagatti U.L.P.S. AMBADAGATTI 18 - Urdu 6 29010200501 29010200503 Govt. 1 5 Class 1 Ambadagatti K.L.P.S AMBADAGATTI AMBADAGATTI 05 - Kannada 7 Habitation : Aravalli---29010200601 29010200601 29010200601 Govt. 1 7 Class 1 Aravalli K.H.P.S. ARAVALLI 05 - Kannada 8 Habitation : Bailawad---29010200801 29010200801 29010200801 Govt. 1 7 Class 1 Bailawad K.H.P.S. BAILWAD 05 - Kannada 9 29010200801 29010200802 Govt. 1 5 Class 1 Bailawad ULPS BAILWAD BAILWAD 18 - Urdu 10 29010200801 29010200804 Pvt Unaided 1 7 Class 1 Bailawad SSKCS BILWAD BAILWAD 05 - Kannada 11 Habitation : Bevinaoppa---29010200901 29010200901 29010200901 Govt. 1 7 Class 1 Bevinaoppa K.H.P.S. BEVINKOPP 05 - Kannada 12 Habitation : Bhairanatti---29010201001 29010201001 29010201001 Govt. -

29/01/2020 Government of Karnataka Page: 88
29/01/2020 GOVERNMENT OF KARNATAKA PAGE: 88 DEPARTMENT OF PRE UNIVERSITY EDUCATION LIST OF PU COLLEGES IN CHIKODI DISTRICT AS ON 29/01/2020 ******************************************************************************** SLNO COLCD NAME AND ADDRESS YEAR OF OPEN & COLL TYPE OPENING & AIDED GO NOS. WITH DATE ******************************************************************************** 1177 DC013 GI BAGEWADI PU COLLEGE 61-62 BIFUR PU COL NIPANI CHIKODI TQ ED 031 UPC 61 DT 30-09-1961 BELGAUM DT 591237 -------------------------------------------------------------------------------- 1178 DC015 GOVT EX-MUNICIPAL PU COL 81-82 GOVT PU COL GOKAK ED 16 SHM 81 DT 01-07-1981 BELGAUM DT 591307 -------------------------------------------------------------------------------- 1179 DC016 SDVS SANGHA'S PU COLLEGE BIFUR PU COL SANKESHWAR HUKKERI TQ BELGAUM DT 591313 -------------------------------------------------------------------------------- 1180 DC018 BASAPRABHUKORE PU COLLEGE 69-70 BIFUR PU COL CHIKODI ANKALI ROAD AC2 GIA-MG 70-71 DT 16-11-1970 BELGAUM DT 591201 -------------------------------------------------------------------------------- 1181 DC025 S S M S PU COLLEGE BIFUR PU COL ATHANI BELGAUM DT 591304 -------------------------------------------------------------------------------- 1182 DC026 SHIVANANDA COLLEGE 67-68 BIFUR PU COL KAGVAD ATHANI TQ ED 94 UAC 67 DT 30-10-1967 BELGAUM DT 591223 -------------------------------------------------------------------------------- 1183 DC028 JA COMP PU COLLEGE 72-73 AIDED PU COL ATHANI ED 19 TPU 72 DT -

Aquifer Map of Gokak Taluk, Belagavi District ´ 1:80,000 GURLAPUR ") PWD IB HALLUR ") ")
Aquifer Map of Gokak Taluk, Belagavi District ´ 1:80,000 GURLAPUR ") PWD IB HALLUR ") ") SHIVAPUR ") KHANHATTI ") MUDALGI ") DHAVLESHWAR ") MUNYAL ") ARLIMATTI MUNYAL ") AURWADI RANGAPUR") ") ") IRALHATTI ") BISANKOP NAGNUR ") TUKANHATTI ") HUNSHYAL DANDAPUR ") ") ") KAMAL DINNI ") HALE TORGUDRI ") MANNAPUR ") RAJAPUR ") JOKANHATTI ") BHAIRANHATTI PAMALDINI ") ") DHARMATTI VENKATAPUR GUJANHATT")I ") ") PATGUNDI ") HOSHATTI ") BADIGWARD YARGUDRI ") SUNDHOLI ") HOSUR ") ") KALLOLI HANMAPU")R GULGANJIKOP DURDUNDI ") ") ") MUSGUPPI ") TIGDI VADERHATTI ") LAKSHMESHWAR TIMMAPUR ") ") ") MALLAPUR ") PHULGADDI KULIGOD KAMANKATTI ") ") ") GHATPRABHA R S ") YADAWAD IB ") SANGANKERI ") KOPPADAHATTI SANATARIUM ") ") ") TALKATNA ARBH")AVI MATH AGRICULTURAL SCHOOL ") ") ") ARBHAVI HONKUPPI NANDGAON ") ") M") UTNAL ") HUNSHAL TAKARHATTI ") ") UDGATTI ") SAVALGI BALABAL ") ") SHINDIKURBET ") KHANDARHATTI ") BIRANGADDI ") DHUPDAL ") GOKAK ROAD R ")S ") RADDERAHATTI KONNUR ") ") HADGINHAL NALLANHATTI MELVANKI ") KAUJALAGI MARADI MATH ") ") KALARKOP ") SHIVAPUR ") ") ") NAIKWADI CHIKDAULI ") ") KAPARHATTI BILKUNDI MANAMI MANIKWADI SINGANAPUR TAKKE ") ") ") ") ") ") BASALIGUNDI GOKAK COTTON MILLS ") LOLSUR ") ADIHATTI ") SAJJIHAL ") ") KALLIGUDDI SINGANAPUR ") ") MAILMATTI ") GOKAK ") PWD REST HOUSE JAPSI ") KEMALKO")L GOSBAL ") LINGAPUR ") ") MANNEKERI ") MALDINNI ") ")UPPARHATTI BETGERI ") BAGARNAL ") GODCHINMALKI ") KARABGATTI ") BENCHINMARDI ") MARDI SHIVAPUR ") AJJANKATTIMAMDAPUR ") ") HANMAPUR SHIGIHOLI HANMAPUR ") PANCHANAGAKANAHATTI ") KOLVI ") ") -

CONGRATULATIONS****** Graduate Engineer Trainee TECHFINIX PVT
Graduate Engineer Trainee ACC Limited ( ACC Concrete RMX Division) Pay Package: 3.6 Lakhs – 4.25 Lakhs SPOORTHY B.R. PREMALATA VADAGE TEJASWINI GHASARI PRIYANKA BASWANI SOUMYA METI AMITRAJ SHETTY SANDEEP SHENGUNSHI MANJUNATH GOUDAR VINAYAK CHAPLE RAHUL KULGUDE SHIVRAJ SHANMUKH SOURABH MEHTA SHIVRAJ M.B. VINAYAK KINAGI ****** CONGRATULATIONS****** Graduate Engineer Trainee TECHFINIX PVT. LTD., MUMBAI Pay Package: 1.56 Lakhs ( For first 6 months) 1.92 Lakhs ( For next 6 months) 2.4 Lakhs ( After one year ) PARASHRAM SHINDOLKAR ARIHANT AMANAJI Graduate Engineer Junior Associate Graduate Engineer Trainee- Civil PwC ( India) Trainee- Civil AFCONS Goregaon East, Mumbai AARBEE STRUCTURES INFRASTRUCTURE LTD. Package : 3.48 Lakhs Pay Package: 2.40 Lakhs Pay Package: 3.90 Lakhs JAYESH NANDYALKAR NAMRATA KAROSHI AMITRAJ SHETTY Assistant System Engineer -Trainee TATA CONSULTANCY SERVICES LTD. Pay Package: 3.4 Lakhs SAGAR GOUDAPPANAVAR VINAYAK KINAGI Graduate Engineer Trainee- Civil Post Graduate Trainee DON CONSTRUCTION CHEMICALS PVT. LTD. ZAMIL STEEL BUILDINGS Pay Package: PVT. LTD., PUNE 2.40 Lakhs ( For first 6 months) Pay Package: 4.00 Lakhs ( After 6 months) 4.00 Lakhs SANTOSHKUMAR SULLAD SUSHMITA LONI BHAMINI GUMAJA M.Tech.( Structures) Graduate Engineer Trainee- Civil ASHOK BUILDCON LTD. Pay Package: 2.4 Lakhs MANJUNATH MATH GURURAJ MANNUR Graduate Assistant Project Graduate Engineer Trainee- Civil Engineer Trainee- Engineer CHAITANYA ASSOCIATES, BELAGAVI Civil INFRA SUPPORT SWASTIK ENGINEERING PVT. CONSTRUCTIONS LTD., BELAGAVI MANJUNATH GOKAK -

Prl. District and Session Judge, Belagavi. Sri
Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL. DISTRICT AND SESSIONS JUDGE BELAGAVI Cause List Date: 16-10-2020 Sr. No. Case Number Timing/Next Date Party Name Advocate 11.00 AM-02.00 PM 1 R.A. 387/2019 Shantadevi Wd/o Virupaxi Shedbal Age Masekar Ratan (NOTICE) 80yrs R/o Pl.No.76,CTS G IA/1/2019 No.219/2B/30,Khanapur Rd,Tilakwadi,BGV. S N Patil Vs Gajendrakumar Virupaxi Shedbal Age 52yrs R/o C/o,S.C.Hiremath,P.No.1868/C,Anjeneya Ng,M.M.Extn.BGV. 2 Misc 23/2020 Vijayabai Sarjerao Deshpande age 87 Joshi O.B. (NOTICE) yrs R/o Gokak Tq Gokak Vs Premabai Ramachandra Deshpande age major R/o Hukkeri since deceased leaving behind no LRs. 3 Misc 72/2020 Ramappa Laxmappa Chougla age 65 yrs Praveen V (NOTICE) R/o Sultanpur Tq Raibag Dt Belagavi Hiremath IA/1/2020 Vs Balappa Shankareppa Mushi age 69 yrs R/o Kappalaguddi tq Raibag Dt Belagavi 4 R.A. 77/2020 Basavaraj Shivarayappa Betageri,Age V.S.Gotakhindi (NOTICE) 54 yrs R/o. Goravanakolla Tq Saundatti IA/1/2020 Belagavi IA/2/2020 Vs Suvarna W/o. Shidramappa Arali Age 57 yrs R/o. 138, Bairidevarkoppa ,Hubbalili, Tq Hubbali Dt Dharw 5 R.A. 125/2020 Siddappa S/o Rudrappa Horatti Age SHRI. NAGRAJ (NOTICE) 58Yrs R/o Nekar Colony, Benakatti, Tq S. TARAGAR, IA/1/2020 Saundatti Dist Belagavi. IA/2/2020 Vs Rudrappa S/o Hanamantappa Kurubar @ Bannur Age 69Yrs R/o Benakatti, tq Saundatti Dist Belagavi. -

Bedkar Veedhi S.O Bengaluru KARNATAKA
pincode officename districtname statename 560001 Dr. Ambedkar Veedhi S.O Bengaluru KARNATAKA 560001 HighCourt S.O Bengaluru KARNATAKA 560001 Legislators Home S.O Bengaluru KARNATAKA 560001 Mahatma Gandhi Road S.O Bengaluru KARNATAKA 560001 Rajbhavan S.O (Bangalore) Bengaluru KARNATAKA 560001 Vidhana Soudha S.O Bengaluru KARNATAKA 560001 CMM Court Complex S.O Bengaluru KARNATAKA 560001 Vasanthanagar S.O Bengaluru KARNATAKA 560001 Bangalore G.P.O. Bengaluru KARNATAKA 560002 Bangalore Corporation Building S.O Bengaluru KARNATAKA 560002 Bangalore City S.O Bengaluru KARNATAKA 560003 Malleswaram S.O Bengaluru KARNATAKA 560003 Palace Guttahalli S.O Bengaluru KARNATAKA 560003 Swimming Pool Extn S.O Bengaluru KARNATAKA 560003 Vyalikaval Extn S.O Bengaluru KARNATAKA 560004 Gavipuram Extension S.O Bengaluru KARNATAKA 560004 Mavalli S.O Bengaluru KARNATAKA 560004 Pampamahakavi Road S.O Bengaluru KARNATAKA 560004 Basavanagudi H.O Bengaluru KARNATAKA 560004 Thyagarajnagar S.O Bengaluru KARNATAKA 560005 Fraser Town S.O Bengaluru KARNATAKA 560006 Training Command IAF S.O Bengaluru KARNATAKA 560006 J.C.Nagar S.O Bengaluru KARNATAKA 560007 Air Force Hospital S.O Bengaluru KARNATAKA 560007 Agram S.O Bengaluru KARNATAKA 560008 Hulsur Bazaar S.O Bengaluru KARNATAKA 560008 H.A.L II Stage H.O Bengaluru KARNATAKA 560009 Bangalore Dist Offices Bldg S.O Bengaluru KARNATAKA 560009 K. G. Road S.O Bengaluru KARNATAKA 560010 Industrial Estate S.O (Bangalore) Bengaluru KARNATAKA 560010 Rajajinagar IVth Block S.O Bengaluru KARNATAKA 560010 Rajajinagar H.O Bengaluru KARNATAKA -

Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL
Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL. DISTRICT AND SESSIONS JUDGE BELAGAVI Cause List Date: 06-10-2020 Sr. No. Case Number Timing/Next Date Party Name Advocate 2.45 PM- 5.45 PM 1 Crl.Misc. 1528/2020 Rayappa S/o Bhimappa Khot Age P.K.HUKKERIMATH (ORDERS) 60yrs R/o Mirapurhatti Tq Chikkodi Dt Belagavi Vs The State of Karnataka Chikkodi PS Rb/y PP Belagavi 2 Crl.Misc. 1543/2020 Umesh Muttappa Bevanur Age A.K.Ingale and (ORDERS) 25Yrs R/o Mavinhatti, Abbihal P.R.Rodabasannavar. Tq Athani Dist Belagavi. Vs The State of Karnataka R/by Its P.P. Belagavi. 1/1 Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL. DISTRICT AND SESSIONS JUDGE BELAGAVI Cause List Date: 06-10-2020 Sr. No. Case Number Timing/Next Date Party Name Advocate 11.00 AM-02.00 PM 1 R.A. 576/2019 Demappa Gangappa Bandagi H.C.Savasuddi (NOTICE) Age 75 yrs R/o IA/1/2019 Inchal,Tq.Saundatti,Dt.Belagavi. IA/2/2019 Vs IA/3/2019 Shivappa Gangappa Bandagi Age 67 yrs R/o Inchal,Tq.Saundatti,Dt.Belagavi. 2 A.S. 9/2018 Rajappa Laxman Bajantri Age Y. G. GUMAJ, (SUMMONS) 45yrs R/o B No , Room NO 149, IA/1/2018 Dar Police Head Quaters S P KULKARNI Belagavi Vs The Shriram Transport Finance Co R/o 1st Flr CTS No.4801/1/A, Behind RTO Office P.B.Road BGV 3 Misc 101/2020 Competent Authority and Sub A.B.BASAPURE (APPEARANCE OF Divisional Magistrate Belagavi PARTY) Sub Div. -
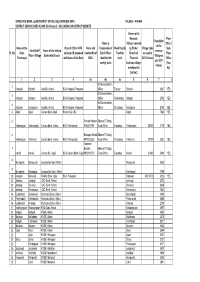
Sl. No. Name of the Gram Panchayat Identified FI Place / Village Name Of
SYNDICATE BANK, LEAD DISTRICT OFFICE, BELGAUM (BIC-0541) TALUKA :- ATHANI DISTRICT SERVICE AREA PLANS (Re-Revised) - UPLOADING ON DISTRICT WEBSITE Names of all Revenue Post Population Name & Villages covered Office / of the Name of the Branch / BCA / ATM Name and Designation of Week Day (S) by BCAs / Village Code Sub- Identified FI Name of the allotted revenue Sl. No. Gram existing OR proposed Contact No.of Bank Officer Fixed for Branch of as used in Post Place / Village Bank with Branch Village as Panchayat with Name of the Bank BCA identified for visits Financial 2011 Census Office per 2001 weekly visits Inclusion villages (Yes / Census mentioned in No) Col.No.2 1 2 3 4 4a 4b 4c 5 6 7 8 Mr.Somashekhar, 1 Katageri Badachi Axis Bk, Athani BCA Katageri, Proposed Officer Tueday Badachi 3387 YES Mr.Somashekhar, 2 Katageri Katageri Axis Bk, Athani BCA Katageri, Proposed Officer Wednesday Katageri 2792 YES Mr.Somashekhar, 3 Katageri Kodaganur Axis Bk, Athani BCA Katageri, Proposed Officer Thursdays Kodaganur 2193 YES 4 Aigali Aigali Canara Bank Aigali Branch Can. Bk. Aigali 7425 YES 5 Santosh Magar Shweta S Totagi, Yalihadagali Yalihadagali Canara Bank, Athani BCA Yalihadagali 9740411581 Rural Officer Tuesdays Yalihadagali 22000 3178 YES 6 Basappa Kiwadi Shweta S Totagi, Yalihadagali Yakkanchi Canara Bank, Athani BCA Yalihadagali 9972025353 Rural Officer Thursdays Yakkanchi 22100 2052 YES Appanna 7 Biradar, Shweta S Totagi, Kohalli Kohalli Canara Bk., Aigali BCA Canara Bank, Aigali 9902013573 Rural Officer Tuesdays Kohalli 21600 5948 YES 8 -
Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL
Prl. District and Session Judge, Belagavi. Sri. Chandrashekhar Mrutyunjaya Joshi PRL. DISTRICT AND SESSIONS JUDGE BELAGAVI Cause List Date: 15-09-2020 Sr. No. Case Number Timing/Next Date Party Name Advocate 11.00 AM-02.00 PM CROSS EXAMINATION OF PW 1 SC 122/2018 State of Karnataka R/by P P PP (EVIDENCE) Belagavi. Vs S N PATTAR Suvarna alias Shivakka Neelappa Ganagi Age 37 yrs R/o Aralikatti Tq Dt Belagavi. 2 SC 280/2018 The State of Karnataka R/by PP PP Belagavi (ACCUSSED Belagavi STATEMENT u/s 313 Vs V K Kallimani CrPC) Sambhaji Yoganna Andhare Age 45 Yrs R/o Yadoga Tq Khanapur Dt Belagavi 3 Crl.Misc. 1282/2020 Suresh Ramappa Dange Age R.G. PATIL (ARGUMENTS) 29Yrs R/o Itanal Village, in Raibag Tq, Dist Bealgavi. Vs The State of Karnataka Through PSI Raibag P.S. R/by Learned P.P. Bealgavi. 4 Crl.Misc. 1323/2020 Basu @ Basavaraj S/o Rudrappa A.C.Dongare. (OBJECTION) Nesaragi Age 27Yrs R/o Killa Gokak Tq Gokak Dt Belagavi. Vs The state of Karnataka R/by P.P. Belagavi 5 Crl.Misc. 1334/2020 Vittal Shankar Kempashetty Age A.S.PATIL (OBJECTION) 25Yrs R/o Balobal Tq Gokak Dist Belagavi. Vs The State of Karnataka Through Gokak Town Police, By Public Prosecutor, Belagavi. 6 Crl.Misc. 1342/2020 Guljar Ahamadsab Desai Age L.S.Kuri (OBJECTION) 55Yrs R/o Ankalagi Tq Gokak Dist Belagavi. Nw/at Malini Ngar, Belagavi. Vs The State of Karnataka R/by P.P. Belagavi. 1/3 Prl. District and Session Judge, Belagavi.