Basic Parameters of Open Star Clusters DOLIDZE 14 and NGC 110 in Infrared Bands
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

LIST of PUBLICATIONS Aryabhatta Research Institute of Observational Sciences ARIES (An Autonomous Scientific Research Institute
LIST OF PUBLICATIONS Aryabhatta Research Institute of Observational Sciences ARIES (An Autonomous Scientific Research Institute of Department of Science and Technology, Govt. of India) Manora Peak, Naini Tal - 263 129, India (1955−2020) ABBREVIATIONS AA: Astronomy and Astrophysics AASS: Astronomy and Astrophysics Supplement Series ACTA: Acta Astronomica AJ: Astronomical Journal ANG: Annals de Geophysique Ap. J.: Astrophysical Journal ASP: Astronomical Society of Pacific ASR: Advances in Space Research ASS: Astrophysics and Space Science AE: Atmospheric Environment ASL: Atmospheric Science Letters BA: Baltic Astronomy BAC: Bulletin Astronomical Institute of Czechoslovakia BASI: Bulletin of the Astronomical Society of India BIVS: Bulletin of the Indian Vacuum Society BNIS: Bulletin of National Institute of Sciences CJAA: Chinese Journal of Astronomy and Astrophysics CS: Current Science EPS: Earth Planets Space GRL : Geophysical Research Letters IAU: International Astronomical Union IBVS: Information Bulletin on Variable Stars IJHS: Indian Journal of History of Science IJPAP: Indian Journal of Pure and Applied Physics IJRSP: Indian Journal of Radio and Space Physics INSA: Indian National Science Academy JAA: Journal of Astrophysics and Astronomy JAMC: Journal of Applied Meterology and Climatology JATP: Journal of Atmospheric and Terrestrial Physics JBAA: Journal of British Astronomical Association JCAP: Journal of Cosmology and Astroparticle Physics JESS : Jr. of Earth System Science JGR : Journal of Geophysical Research JIGR: Journal of Indian -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

Cas – Objektauswahl NGC
Cas – Objektauswahl NGC NGC 0103 NGC 0278 NGC 0637 NGC 7635 NGC 0110 NGC 0281 NGC 0654 NGC 7654 NGC 0129 NGC 0366 NGC 0657 NGC 7788 NGC 0133 NGC 0381 NGC 0659 NGC 7789 NGC 0136 NGC 0433 NGC 0663 NGC 7790 NGC 0146 NGC 0436 NGC 0743 NGC 0147 NGC 0457 NGC 0886 NGC 0185 NGC 0559 NGC 0896 Sternbild- NGC 0189 NGC 0581 NGC 1027 Übersicht NGC 0225 NGC 0609 NGC 1343 Zur Objektauswahl: Nummer anklicken Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken Cas Übersichtskarte Auswahl N103_129_133_136_146_189_225 Aufsuchkarte Auswahl Auswahl NGC 0103_NGC 0136 Übersichtskarte 0103_NGC NGC Aufsuch- karte Auswahl NGC 0129 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 0133_NGC 0146 Übersichtskarte 0133_NGC NGC Aufsuch- karte Auswahl NGC 0189 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 0225 ÜbersichtskarteNGC Aufsuch- karte NGC 0110 Aufsuchkarte Auswahl Auswahl NGC 0110 ÜbersichtskarteNGC Aufsuch- karte NGC 0147_NGC 0185_NGC 0278 Aufsuchkarte Auswahl Auswahl NGC 147 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 185 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 278 ÜbersichtskarteNGC Aufsuch- karte NGC 0281 Aufsuchkarte Auswahl Auswahl NGC 0281 ÜbersichtskarteNGC Aufsuch- karte NGC 0366_NGC 0381 Aufsuchkarte Auswahl Auswahl NGC 0366_NGC 0381 Übersichtskarte 0366_NGC NGC Aufsuch- karte N 433_N 436_N 457_N 581 Aufsuchkarte Auswahl Auswahl NGC 0433 ÜbersichtskarteNGC Aufsuch- karte Auswahl NGC 0436_NGC 0457 Übersichtskarte 0436_NGC NGC Aufsuch- karte Auswahl NGC 0581 ÜbersichtskarteNGC Aufsuch- karte N -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

My Finest NGC Album
My Finest NGC Album A detailed record of my journey through The Royal Astronomical Society of Canada’s Finest NGC list Name: ______________________________ Centre or Home Location: ______________________________ The New General Catalogue or NGC contains 7,840 entries and forms the core of most people's " life list" of observing targets. The NGC was originally published in 1888 by J.L.E. Dreyer and therefore predated photographic astronomy. The Finest NGC list, compiled by Alan Dyer complements the Messier List, as there is no overlap. The list features many fine deep-sky treasures as well as a few somewhat more challenging objects. Once you have observed all of the objects on this list, application forms can be found on the RASC website at www.rasc.ca. The FNGC certificate has been awarded since 1995. Here is an overview of the Finest NGC Observing List Finest NGC Objects Number Notes Open Clusters 12 Including the famous Double Cluster in Perseus, NGC 7789 in Cassiopeia, and NGC 6633 in Ophiuchus. Globular Clusters 2 NGC 5466 in Bootes and NGC 6712 in Scutum. Diffuse Nebulae 14 Includes the great Veil Nebula as well as the North America and Rosette nebulae. Planetary Nebulae 24 Includes many fine PN's like the Ghost of Jupiter, the Cat's Eye, the Blinking Planetary, the Helix, the Blue Snowball, and the Clown Face nebulae. Galaxies 58 Includes the amazing NGC 4565 in Coma Berenices, NGC 253 in Sculptor, and NGC 5907 in Draco. Total 110 The Finest NGC list can be started during any season. Why Record Your Observations? Recording observations is important for two reasons. -

My Finest NGC Album
My Finest NGC Album A detailed record of my journey through The Royal Astronomical Society of Canada’s Finest NGC list Name: ______________________________ Centre or Home Location: ______________________________ The New General Catalogue or NGC contains 7,840 entries and forms the core of most people's "life list" of observing targets. The NGC was originally published in 1888 by J.L.E. Dreyer and therefore predated photographic astronomy. The Finest NGC list, compiled by Alan Dyer complements the Messier List, as there is no overlap. The list features many fine deep-sky treasures as well as a few somewhat more challenging objects. Once you have observed all of the objects on this list, application forms can be found on the RASC website at www.rasc.ca. The FNGC certificate has been awarded since 1995. Here is an overview of the Finest NGC Observing List Finest NGC Objects Number Notes Open Clusters 12 Including the famous Double Cluster in Perseus, NGC 7789 in Cassiopeia, and NGC 6633 in Ophiuchus. Globular Clusters 2 NGC 5466 in Bootes and NGC 6712 in Scutum. Diffuse Nebulae 14 Includes the great Veil Nebula as well as the North America and Rosette nebulae. Planetary Nebulae 24 Includes many fine PN's like the Ghost of Jupiter, the Cat's Eye, the Blinking Planetary, the Helix, the Blue Snowball, and the Clown Face nebulae. Galaxies 58 Includes the amazing NGC 4565 in Coma Berenices, NGC 253 in Sculptor, and NGC 5907 in Draco. Total 110 The Finest NGC list can be started during any season. Why Record Your Observations? Recording observations is important for two reasons. -
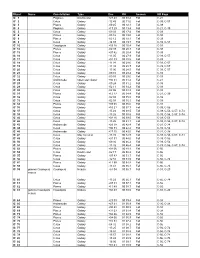
HB-NGC Index
Object Name Constellation Type Dec RA Season HB Page IC 1 Pegasus Double star +27 43 00 08.4 Fall C-21 IC 2 Cetus Galaxy -12 49 00 11.0 Fall C-39, C-57 IC 3 Pisces Galaxy -00 25 00 12.1 Fall C-39 IC 4 Pegasus Galaxy +17 29 00 13.4 Fall C-21, C-39 IC 5 Cetus Galaxy -09 33 00 17.4 Fall C-39 IC 6 Pisces Galaxy -03 16 00 19.0 Fall C-39 IC 8 Pisces Galaxy -03 13 00 19.1 Fall C-39 IC 9 Cetus Galaxy -14 07 00 19.7 Fall C-39, C-57 IC 10 Cassiopeia Galaxy +59 18 00 20.4 Fall C-03 IC 12 Pisces Galaxy -02 39 00 20.3 Fall C-39 IC 13 Pisces Galaxy +07 42 00 20.4 Fall C-39 IC 16 Cetus Galaxy -13 05 00 27.9 Fall C-39, C-57 IC 17 Cetus Galaxy +02 39 00 28.5 Fall C-39 IC 18 Cetus Galaxy -11 34 00 28.6 Fall C-39, C-57 IC 19 Cetus Galaxy -11 38 00 28.7 Fall C-39, C-57 IC 20 Cetus Galaxy -13 00 00 28.5 Fall C-39, C-57 IC 21 Cetus Galaxy -00 10 00 29.2 Fall C-39 IC 22 Cetus Galaxy -09 03 00 29.6 Fall C-39 IC 24 Andromeda Open star cluster +30 51 00 31.2 Fall C-21 IC 25 Cetus Galaxy -00 24 00 31.2 Fall C-39 IC 29 Cetus Galaxy -02 11 00 34.2 Fall C-39 IC 30 Cetus Galaxy -02 05 00 34.3 Fall C-39 IC 31 Pisces Galaxy +12 17 00 34.4 Fall C-21, C-39 IC 32 Cetus Galaxy -02 08 00 35.0 Fall C-39 IC 33 Cetus Galaxy -02 08 00 35.1 Fall C-39 IC 34 Pisces Galaxy +09 08 00 35.6 Fall C-39 IC 35 Pisces Galaxy +10 21 00 37.7 Fall C-39, C-56 IC 37 Cetus Galaxy -15 23 00 38.5 Fall C-39, C-56, C-57, C-74 IC 38 Cetus Galaxy -15 26 00 38.6 Fall C-39, C-56, C-57, C-74 IC 40 Cetus Galaxy +02 26 00 39.5 Fall C-39, C-56 IC 42 Cetus Galaxy -15 26 00 41.1 Fall C-39, C-56, C-57, C-74 IC -

Observer Le Ciel En Octobre 2018
OBSERVER LE CIEL EN OCTOBRE 2018 LE CIEL D'AUTOMNE ET NOTRE AMAS LOCAL En tout début de nuit de ce mois d'octobre, ce sont encore les constellations du ciel d'été qui dominent la voûte céleste : Le Bouvier, avec l'éclatante Arcturus suivi de Hercule sur l'hori- zon ouest, puis au zénith le somptueux triangle d'été marqué par les brillants jalons, d'abord Véga de la constellation de la Lyre au zénith, puis plus au sud est, Deneb du Cygne, puis au sud, Altaïr de l'Aigle. Ce mois d'octobre 2018 est encore marqué par la présence de deux belles planètes de notre sys- tème solaire : tout d'abord Saturne, entre le méridien et l'ho- rizon ouest et enfin, presque au méridien, la star de l'été, Mars, la planète rouge, exceptionnellement brillante, ce qui est du à son exceptionnelle proximité de la Terre en 2018. Précisons cependant que ces deux planètes sont situées assez basses sur l'horizon sud car l'écliptique d'été traverse les constellations les plus australes du zodiaque. Pour admirer ces deux bijoux planétaires, il faut disposer d'une petite lunette astronomique ou mieux encore d'un téles- cope, même de faible puissance, le but étant de disposer d'un instrument offrant des amplifications d'au moins 50 à 80 fois. Avec de tels grossissements, on pourra sans problème aper- cevoir les magnifiques anneaux de Saturne, et si le ciel est clément, pas trop turbulent, et si la tempête de poussière qui a sévi sur l'ensemble de la planète depuis juin dernier s'est to- Lettre d'Information IMCCE – Septembre 2018 talement estompée, on pourra voir la calotte polaire de Mars et quelques éléments de sa surface. -

A Catalog of 120 Ngc Open Star Clusters
Journal of The Korean Astronomical Society doi:10.5303/JKAS.2011.44.1.1 44: 1 ∼ 11, 2011 February ISSN:1225-4614 °c 2011 The Korean Astronomical Society. All Rights Reserved. http://jkas.kas.org A CATALOG OF 120 NGC OPEN STAR CLUSTERS A. L. Tadross National Research Institute of Astronomy and Geophysics, 11421 - Helwan, Cairo, Egypt E-mail: [email protected] (Received November 02, 2010; Revised November 18, 2010; Accepted December 01, 2010) ABSTRACT A sample of 145 JHK–2MASS observations of NGC open star clusters is studied, of which 132 have never been studied before. Twelve are classified as non-open clusters and 13 are re-estimated self-consistently, after applying the same methods in order to compare and calibrate our reduction procedures. The fundamental and structural parameters of the 120 new open clusters studied here are derived using color-magnitude diagrams of JHK Near-IR photometry with the fitting of solar metallicity isochrones. We provide here, for the first time, a catalog of the main parameters for these 120 open clusters, namely, diameter, distance, reddening and age. Key words : Galaxy: open clusters and associations — individual: NGC — astrometry — Stars — astronomical databases: catalogs 1. INTRODUCTION can be improved. The JHK Near-IR 2MASS catalog has the advantage Systematic studies of open star clusters (OCs) are of being a homogeneous database, enabling us to ob- very important for understanding galactic structure serve young clusters in their dusty environments and and star formation processes, as well as stellar evo- reach their outer regions where low mass stars dom- lution and evolution of the Galactic disk. -

Arxiv:1108.2134V2
Journal of The Korean Astronomical Society 44: 1 ∼ 11, 2011 doi:10.5303/JKAS.2011.44.1.1 A CATALOG OF 120 NGC OPEN STAR CLUSTERS A. L. Tadross National Research Institute of Astronomy & Geophysics, Helwan, Cairo, Egypt. email: [email protected] Abstract A sample of 145 JHK–2MASS observations of NGC open star clusters is studied, of which 132 have never been studied before. Twelve are classified as non-open clusters and 13 are re-estimated self-consistently, after applying the same methods in order to compare and calibrate our reduction procedures. The fundamental and structural parameters of the 120 new open clusters studied here are derived using color-magnitude diagrams of JHK Near-IR photometry with the fitting of solar metallicity isochrones. We provide here, for the first time, a catalog of the main parameters for these 120 open clusters, namely, diameter, distance, reddening and age. Keywords: Galaxy: open clusters and associations — individual: NGC — astrometry — Stars — astronom- ical databases: catalogs 1 INTRODUCTION Systematic studies of open star clusters (OCs) are very important for understanding galactic structure and star formation processes, as well as stellar evolution and evolution of the Galactic disk. By utilizing color-magnitude diagrams (CMDs) of the stars observed in the near-infrared (NIR) bands, it is possible to determine the properties of open clusters such as distance, reddening, age and metallicity. Such parameters are necessary for studying clusters and Galactic disk. The Galactic (radial and vertical) abundance gradient also can be studied using OCs (Hou, Prantzos, & Boissier 2000; Chen, Hou, & Wang 2003; Kim & Sung 2003; Tadross 2003; Kim et al. -

A Catalog of 120 Ngc Open Star Clusters
Journal of The Korean Astronomical Society doi:10.5303/JKAS.2011.44.1.1 44: 1 » 11, 2011 February ISSN:1225-4614 °c 2011 The Korean Astronomical Society. All Rights Reserved. http://jkas.kas.org A CATALOG OF 120 NGC OPEN STAR CLUSTERS A. L. Tadross National Research Institute of Astronomy and Geophysics, 11421 - Helwan, Cairo, Egypt E-mail: [email protected] (Received November 02, 2010; Revised November 18, 2010; Accepted December 01, 2010) ABSTRACT A sample of 145 JHK{2MASS observations of NGC open star clusters is studied, of which 132 have never been studied before. Twelve are classi¯ed as non-open clusters and 13 are re-estimated self-consistently, after applying the same methods in order to compare and calibrate our reduction procedures. The fundamental and structural parameters of the 120 new open clusters studied here are derived using color-magnitude diagrams of JHK Near-IR photometry with the ¯tting of solar metallicity isochrones. We provide here, for the ¯rst time, a catalog of the main parameters for these 120 open clusters, namely, diameter, distance, reddening and age. Key words : Galaxy: open clusters and associations | individual: NGC | astrometry | Stars | astronomical databases: catalogs 1. INTRODUCTION can be improved. The JHK Near-IR 2MASS catalog has the advantage Systematic studies of open star clusters (OCs) are of being a homogeneous database, enabling us to ob- very important for understanding galactic structure serve young clusters in their dusty environments and and star formation processes, as well as stellar evo- reach their outer regions where low mass stars dom- lution and evolution of the Galactic disk. -

I N S I D E T H I S I S S
Publications and Products of June/juin 2000 Volume/volume 94 Number/numéro 3 [683] The Royal Astronomical Society of Canada Observer’s Calendar — 2000 This calendar was created by members of the RASC. All photographs were taken by amateur astronomers using ordinary camera lenses and small telescopes and represent a wide spectrum of objects. An informative caption accompanies every photograph. The Journal of the Royal Astronomical Society of Canada Le Journal de la Société royale d’astronomie du Canada It is designed with the observer in mind and contains comprehensive astronomical data such as daily Moon rise and set times, significant lunar and planetary conjunctions, eclipses, and meteor showers. The 1998, 1999, and 2000 editions each won the Best Calendar Award from the Ontario Printing and Imaging Association. (designed and produced by Rajiv Gupta) Price: $14.95 (members); $16.95 (non-members) (includes taxes, postage and handling) The Beginner’s Observing Guide This guide is for anyone with little or no experience in observing the night sky. Large, easy to read star maps are provided to acquaint the reader with the constellations and bright stars. Basic information on observing the moon, planets and eclipses through the year 2005 is provided. There is also a special section to help Scouts, Cubs, Guides and Brownies achieve their respective astronomy badges. Written by Leo Enright (160 pages of information in a soft-cover book with otabinding which allows the book to lie flat). Price: $15 (includes taxes, postage and handling) Promotional Items The RASC has many fine promotional items that sport the National Seal.