Gravitational Waves from Dark Sectors, Oscillating Inflatons
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ligo-India Proposal for an Interferometric Gravitational-Wave Observatory
LIGO-INDIA PROPOSAL FOR AN INTERFEROMETRIC GRAVITATIONAL-WAVE OBSERVATORY IndIGO Indian Initiative in Gravitational-wave Observations PROPOSAL FOR LIGO-INDIA !"#!$ Indian Initiative in Gravitational wave Observations http://www.gw-indigo.org II Title of the Project LIGO-INDIA Proposal of the Consortium for INDIAN INITIATIVE IN GRAVITATIONAL WAVE OBSERVATIONS IndIGO to Department of Atomic Energy & Department of Science and Technology Government of India IndIGO Consortium Institutions Chennai Mathematical Institute IISER, Kolkata IISER, Pune IISER, Thiruvananthapuram IIT Madras, Chennai IIT, Kanpur IPR, Bhatt IUCAA, Pune RRCAT, Indore University of Delhi (UD), Delhi Principal Leads Bala Iyer (RRI), Chair, IndIGO Consortium Council Tarun Souradeep (IUCAA), Spokesperson, IndIGO Consortium Council C.S. Unnikrishnan (TIFR), Coordinator Experiments, IndIGO Consortium Council Sanjeev Dhurandhar (IUCAA), Science Advisor, IndIGO Consortium Council Sendhil Raja (RRCAT) Ajai Kumar (IPR) Anand Sengupta(UD) 10 November 2011 PROPOSAL FOR LIGO-INDIA II PROPOSAL FOR LIGO-INDIA LIGO-India EXECUTIVE SUMMARY III PROPOSAL FOR LIGO-INDIA IV PROPOSAL FOR LIGO-INDIA This proposal by the IndIGO consortium is for the construction and subsequent 10- year operation of an advanced interferometric gravitational wave detector in India called LIGO-India under an international collaboration with Laser Interferometer Gravitational–wave Observatory (LIGO) Laboratory, USA. The detector is a 4-km arm-length Michelson Interferometer with Fabry-Perot enhancement arms, and aims to detect fractional changes in the arm-length smaller than 10-23 Hz-1/2 . The task of constructing this very sophisticated detector at the limits of present day technology is facilitated by the amazing opportunity offered by the LIGO Laboratory and its international partners to provide the complete design and all the key components required to build the detector as part of the collaboration. -

View Print Program (Pdf)
PROGRAM November 3 - 5, 2016 Hosted by Sigma Pi Sigma, the physics honor society 2016 Quadrennial Physics Congress (PhysCon) 1 31 Our students are creating the future. They have big, bold ideas and they come to Florida Polytechnic University looking for ways to make their visions a reality. Are you the next? When you come to Florida Poly, you’ll be welcomed by students and 3D faculty who share your passion for pushing the boundaries of science, PRINTERS technology, engineering and math (STEM). Florida’s newest state university offers small classes and professors who work side-by-side with students on real-world projects in some of the most advanced technology labs available, so the possibilities are endless. FLPOLY.ORG 2 2016 Quadrennial Physics Congress (PhysCon) Contents Welcome ........................................................................................................................... 4 Unifying Fields: Science Driving Innovation .......................................................................... 7 Daily Schedules ............................................................................................................. 9-11 PhysCon Sponsors .............................................................................................................12 Planning Committee & Staff ................................................................................................13 About the Society of Physics Students and Sigma Pi Sigma ���������������������������������������������������13 Previous Sigma Pi Sigma -

The Perils of Complacency
THE PERILS OF COMPLACENCYTHE PERILS : America at a Tipping Point in Science & Engineering : America at a Tipping Point THE PERILS OF COMPLACENCY America at a Tipping Point in Science & Engineering An Update to Restoring the Foundation: The Vital Role of Research in Preserving the American Dream AMERICAN ACADEMY OF ARTS & SCIENCES AMERICAN ACADEMY THE PERILS OF COMPLACENCY America at a Tipping Point in Science & Engineering An Update to Restoring the Foundation: The Vital Role of Research in Preserving the American Dream american academy of arts & sciences Cambridge, Massachusetts This report and its supporting data were finalized in April 2020. While some new data have been released since then, the report’s findings and recommendations remain valid. Please note that Figure 1 was based on nsf analysis, which used existing oecd purchasing power parity (ppp) to convert U.S. and Chinese financial data.oecd adjusted its ppp factors in May 2020. The new factors for China affect the curves in the figure, pushing the China-U.S. crossing point toward the end of the decade. This development is addressed in Appendix D. © 2020 by the American Academy of Arts & Sciences All rights reserved. isbn: 0- 87724- 134- 1 This publication is available online at www.amacad.org/publication/perils-of-complacency. The views expressed in this report are those held by the contributors and are not necessarily those of the Officers and Members of the American Academy of Arts and Sciences. Please direct inquiries to: American Academy of Arts and Sciences 136 Irving Street Cambridge, Massachusetts 02138- 1996 Telephone: 617- 576- 5000 Email: [email protected] Website: www.amacad.org Contents Acknowledgments 5 Committee on New Models for U.S. -

Rainer Weiss, Professor of Physics Emeritus and 2017 Nobel Laureate
Giving to the Department of Physics by Erin McGrath RAINER WEISS ’55, PHD ’62 Bryce Vickmark Rai Weiss has established a fellowship in the Physics Department because he is eternally grateful to his advisor, the late Jerrold Zacharias, for all that he did for Rai, so he knows firsthand the importance of supporting graduate students. Rainer Weiss, Professor of Physics Emeritus and 2017 Nobel Laureate. Rainer “Rai” Weiss was born in Berlin, Germany in 1932. His father was a physician and his mother was an actress. His family was forced out of Germany by the Nazis since his father was Jewish and a Communist. Rai, his mother and father fled to Prague, Czecho- slovakia. In 1937 a sister was born in Prague. In 1938, after Chamberlain appeased Hitler by effectively giving him Czechoslovakia, the family was able to obtain visas to enter the United States through the Stix Family in St. Louis, who were giving bond to professional Jewish emigrants. When Rai was 21 years-old, he visited Mrs. Stix and thanked her for what she had done for his family. The family immigrated to New York City. Rai’s father had a hard time passing the medi- cal boards because of his inability to answer multiple choice exams. His mother, who Rai says “held the family together,” worked in a number of retail stores. Through the services of an immigrant relief organization Rai received a scholarship to attend the prestigious Columbia Grammar School. At the end of 1945, when Rai was 13 years old, he became fascinated with electronics and music. -
Physics of LIGO Lecture 4
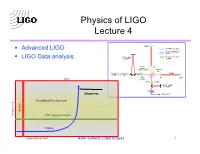
Physics of LIGO Lecture 4 40KG § Advanced LIGO SAPPHIRE, 31.4CMf SILICA, HERAEUS SV 35CMf INPUT MODE SILICA, LIGO I GRADE § LIGO Data analysis CLEANER ~26CMf ACTIVE THERMAL CORRECTION T=0.5% 125W 830KW LASER MOD. BS PRM ITM ETM time T~6% SRM T=7% OUTPUT MODE CLEANER PD Ringdowns GW READOUT Broadband Background Bursts frequency CW (quasi-periodic) Chirps LIGO-G000165-00-R AJW, Caltech, LIGO Project 1 Initial LIGO Þ Advanced LIGO schedule 1995 NSF Funding secured ($360M) 1996 Construction Underway (mostly civil) 1997 Facility Construction (vacuum system) 1998 Interferometer Construction (complete facilities) 1999 Construction Complete (interferometers in vacuum) 2000 Detector Installation (commissioning subsystems) 2001 Commission Interferometers (first coincidences) 2002 Sensitivity studies (initiate LIGO I Science Run) 2003+ Initial LIGO data run (one year integrated data at h ~ 10-21) 2007 Begin Advanced LIGO installation 2008 Advanced LIGO science run (2.5 hours ~ 1 year of Initial LIGO) LIGO-G000165-00-R AJW, Caltech, LIGO Project 2 Advanced LIGO incremental improvements § Reduce shot noise: higher power CW-laser: 12 watts Þ120 watts § Reduce shot noise: Advanced optical configuration: signal recycling mirror (7th suspended optic) to tune shot-noise response in frequency § Reduce seismic noise: Advanced (active) seismic isolation. Seismic wall moved from 40 Hz Þ ~ 12 Hz. § Reduce seismic and suspension noise: Quadrupal pendulum suspensions to filter environmental noise in stages. § Reduce suspension noise: Fused silica fibers, silica welds. § Reduce test mass thermal noise: Last pendulum stage (test mass) is controlled via electrostatic or photonic forces (no magnets). § Reduce test mass thermal noise: High-Q material (40 kg sapphire). -

National Science Foundation LIGO FACTSHEET NSF and the Laser Interferometer Gravitational-Wave Observatory
e National Science Foundation LIGO FACTSHEET NSF and the Laser Interferometer Gravitational-Wave Observatory In 1916, Albert What is LIGO? Einstein published the LIGO consists of two widely separated laser paper that predicted interferometers located within the United States – one gravitational waves – in Hanford, Washington, and the other in Livingston, ripples in the fabric of Louisiana – each housed inside an L-shaped, ultra-high space-time resulting vacuum tunnel. The twin LIGO detectors operate in from the most violent unison to detect gravitational waves. Caltech and MIT phenomena in our led the design, construction and operation of the NSF- universe, from funded facilities. supernovae explosions to the collision of black What are gravitational waves? holes. For 100 years, Gravitational waves are distortions of the space and that prediction has time which emit when any object that possesses mass stimulated scientists accelerates. This can be compared in some ways to how around the world who accelerating charges create electromagnetic fields (e.g. have been seeking light and radio waves) that antennae detect. To generate to directly detect gravitational waves that can be detected by LIGO, the gravitational waves. objects must be highly compact and very massive, such as neutron stars and black holes. Gravitational-wave In the 1970s, the National Science Foundation (NSF) detectors act as a “receiver.” Gravitational waves travel joined this quest and began funding the science to Earth much like ripples travel outward across a pond. and technological innovations behind the Laser However, these ripples in the fabric of space-time carry Interferometer Gravitational-Wave Observatory (LIGO), information about their violent origins and about the the instruments that would ultimately yield a direct nature of gravity – information that cannot be obtained detection of gravitational waves. -

A Brief History of Gravitational Waves
Review A Brief History of Gravitational Waves Jorge L. Cervantes-Cota 1, Salvador Galindo-Uribarri 1 and George F. Smoot 2,3,4,* 1 Department of Physics, National Institute for Nuclear Research, Km 36.5 Carretera Mexico-Toluca, Ocoyoacac, Mexico State C.P.52750, Mexico; [email protected] (J.L.C.-C.); [email protected] (S.G.-U.) 2 Helmut and Ana Pao Sohmen Professor at Large, Institute for Advanced Study, Hong Kong University of Science and Technology, Clear Water Bay, 999077 Kowloon, Hong Kong, China. 3 Université Sorbonne Paris Cité, Laboratoire APC-PCCP, Université Paris Diderot, 10 rue Alice Domon et Leonie Duquet 75205 Paris Cedex 13, France. 4 Department of Physics and LBNL, University of California; MS Bldg 50-5505 LBNL, 1 Cyclotron Road Berkeley, CA 94720, USA. * Correspondence: [email protected]; Tel.:+1-510-486-5505 Abstract: This review describes the discovery of gravitational waves. We recount the journey of predicting and finding those waves, since its beginning in the early twentieth century, their prediction by Einstein in 1916, theoretical and experimental blunders, efforts towards their detection, and finally the subsequent successful discovery. Keywords: gravitational waves; General Relativity; LIGO; Einstein; strong-field gravity; binary black holes 1. Introduction Einstein’s General Theory of Relativity, published in November 1915, led to the prediction of the existence of gravitational waves that would be so faint and their interaction with matter so weak that Einstein himself wondered if they could ever be discovered. Even if they were detectable, Einstein also wondered if they would ever be useful enough for use in science. -

50 Years of Pulsars: Jocelyn Bell Burnell an Interview P
LIGO Scientific Collaboration Scientific LIGO issue 11 9/2017 LIGO MAGAZINE O2: Third Detection! 10:11:58.6 UTC, 4 January 2017 ELL F, H O L P IS L A E ! Y B D O O G 50 Years of Pulsars: Jocelyn Bell Burnell An interview p. 6 The Search for Continuous Waves To name a neutron star p.10 ... and in 1989: The first joint interferometric observing run p. 26 Before the Merger: Spiraling Black Holes Front cover image: Artist’s conception shows two merging black holes similar to those detected by LIGO. The black holes are spinning in a non-aligned fashion, which means they have different orientations relative to the overall orbital motion of the pair. LIGO found a hint of this phenomenon in at least one black hole of the GW170104 system. Image: LIGO/Caltech/MIT/Sonoma State (Aurore Simonnet) Image credits Front cover main image – Credit: LIGO/Caltech/MIT/Sonoma State (Aurore Simonnet) Front cover inset LISA – Courtesy of LISA Consortium/Simon Barke Front cover inset of Jocelyn Bell Burnell and the 4 acre telescope c 1967 courtesy Jocelyn Bell Burnell. Front cover inset of the supernova remnant G347.3-0.5 – Credit: Chandra: NASA/CXC/SAO/P.Slane et al.; XMM-Newton:ESA/RIKEN/J.Hiraga et al. p. 3 Comic strip by Nutsinee Kijbunchoo p. 4-5 Photos by Matt Gush, Bryce Vickmark and Josh Meister p. 6 Jocelyn Bell Burnell and the 4 acre telescope courtesy Jocelyn Bell Burnell. Paper chart analysis courtesy Robin Scagell p. 8 Pulsar chart recordings courtesy Mullard Radio Astronomy Observatory p. -

Fall 2016 for Basic Research in Science
The Adolph C. and Mary Sprague Newsletter MILLER INSTITUTE Fall 2016 for Basic Research in Science Understanding Dark Energy and Neutrinos Inside this edition: from the South Pole Miller Fellow Focus 1-3 From the Executive Director 4 Miller Fellow Focus: Tijmen de Haan Call for Nominations 5 odern cosmology provides an 6 Mincredibly powerful description In the News of the universe we live in. The stan- 20th Annual Symposium 7 dard model of Big Bang cosmology 8 takes only a few assumptions about Next Steps & Birth Announcements the physical laws and initial condi- tions, and makes a wealth of predic- Call for Nominations: tions. As our techniques for measur- ing the large-scale properties of the Miller Research Fellowship universe improve, the observations are found to be consistent with the Nominations predictions of the standard model Deadline: Saturday, September 10, 2016 of Big Bang cosmology time and time again. However, several open ques- Miller Research Professorship tions remain. Applications e can also use our measure- Deadline: Thursday, September 15, 2016 n the late 1990s, we learned that the Wments of the expansion rate Iexpansion of the universe is current- and growth of structure in the uni- Visiting Miller Professorship ly accelerating. This is due to a mysteri- verse to determine the properties of Departmental Nominations ous type of energy cosmologists have its contents. Around the turn of the Deadline: Friday, September 16, 2016 termed dark energy. This discovery millenium, neutrinos, long thought to led to the 2011 Nobel Prize in Phys- be massless particles, were found to See page 5 for more details. -

Project Description Advanced LIGO: Context and Overview
LIGO M030023-00M Project Description Advanced LIGO: Context and Overview Advanced LIGO Gravitational waves offer a remarkable opportunity to see the universe from a new perspective, providing access to astrophysical insights that are available in no other way. The initial LIGO gravitational wave detectors have started observations, and are already yielding data that are being interpreted to establish new upper limits on gravitational-wave flux. The sensitivity of the initial LIGO instruments is such that it is perfectly possible that discoveries will be made. If they succeed, there will be a strong demand from the community to improve the sensitivity allowing more astrophysical information to be recovered from the signals. If no discovery is made, there will be no lesser urgency to improve the sensitivity of the instrument to the point where there is a general consensus that gravitational waves will be detected often and with a good signal-to-noise ratio. The development of the next generation of instrument must be pursued aggressively to make the transition from the initial to the Advanced detector in a timely way – after the complete science run of the initial detector, but as quickly as possible thereafter. The Advanced LIGO detector upgrade meets these requirements for an instrument that will establish gravitational-wave astronomy. It is more than ten times more sensitive, and over a much broader frequency band, than initial LIGO. It can see a volume of space more than a thousand times greater than initial LIGO, and extends the range of compact masses that can be observed at a fixed signal strength by a factor of four or more. -

How to Measure Displacements of 10-19 Meters
The technology behind LIGO: how to measure displacements of 10-19 meters The LIGO interferometers Interferometry: displacement sensing Noise limits Advanced LIGO "Colliding Black Holes" National Center for Supercomputing Applications (NCSA) 4pm today, 1 West: Results from science runs Alan Weinstein, Caltech AJW, UTeV, October 28, 2005 Gravitational wave detectors • Bar detectors • Invented and pursued by Joe Weber in the 60’s • Essentially, a large “bell”, set ringing (at ~ 900 Hz) by GW • Challenge: reduce noise (thermal ringing, readout) • Michelson interferometers • At least 4 independent discovery of method: • Pirani `56, Gerstenshtein and Pustovoit, Weber, Weiss `72 • Pioneering work by Weber and Robert Forward, in 60’s • Now: large, earth-based detectors. Soon: space-based (LISA). AJW, UTeV, October 28, 2005 Resonant bar detectors AURIGA bar near Padova, Italy (typical of some ~5 around the world – Maryland, LSU, Rome, CERN, UWA) 2.3 tons of Aluminum, 3m long; Cooled to 0.1K with dilution fridge in LHe cryostat Q = 4×106 at < 1K Fundamental resonant mode at ~900 Hz; narrow bandwidth Ultra-low-noise capacitive transducer and electronics (SQUID) AJW, UTeV, October 28, 2005 Resonant Bar detectors around the world International Gravitational Event Collaboration (IGEC) Baton Rouge, Legarno, CERN, Frascati, Perth, LA USA Italy Suisse Italy Australia AJW, UTeV, October 28, 2005 Interferometric detection of GWs GW acts on freely mirrors falling masses: laser Beam For fixed ability to splitter Dark port measure ΔL, make L photodiode -

Mathematics People
NEWS Mathematics People “In 1972, Rainer Weiss wrote down in an MIT report his Weiss, Barish, and ideas for building a laser interferometer that could detect Thorne Awarded gravitational waves. He had thought this through carefully and described in detail the physics and design of such an Nobel Prize in Physics instrument. This is typically called the ‘birth of LIGO.’ Rai Weiss’s vision, his incredible insights into the science and The Royal Swedish Academy of Sci- challenges of building such an instrument were absolutely ences has awarded the 2017 Nobel crucial to make out of his original idea the successful Prize in Physics to Rainer Weiss, experiment that LIGO has become. Barry C. Barish, and Kip S. Thorne, “Kip Thorne has done a wealth of theoretical work in all of the LIGO/Virgo Collaboration, general relativity and astrophysics, in particular connected for their “decisive contributions to with gravitational waves. In 1975, a meeting between the LIGO detector and the observa- Rainer Weiss and Kip Thorne from Caltech marked the tion of gravitational waves.” Weiss beginning of the complicated endeavors to build a gravi- receives one-half of the prize; Barish tational wave detector. Rai Weiss’s incredible insights into and Thorne share one-half. the science and challenges of building such an instrument Rainer Weiss combined with Kip Thorne’s theoretical expertise with According to the prize citation, gravitational waves, as well as his broad connectedness “LIGO, the Laser Interferometer with several areas of physics and funding agencies, set Gravitational-Wave Observatory, is the path toward a larger collaboration.