DOCSLIB.ORG

On Products of Gaussian Random Variables

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
On Products of Gaussian Random Variables On products of Gaussian random variables Zeljkaˇ Stojanac∗1, Daniel Suessy1, and Martin Klieschz2 1Institute for Theoretical Physics, University of Cologne, Germany 2 Institute of Theoretical Physics and Astrophysics, University of Gda´nsk,Poland May 29, 2018 Sums of independent random variables form the basis of many fundamental theorems in probability theory and statistics, and therefore, are well understood. The related problem of characterizing products of independent random variables seems to be much more challenging. In this work, we investigate such products of normal random vari- ables, products of their absolute values, and products of their squares. We compute power-log series expansions of their cumulative distribution function (CDF) based on the theory of Fox H-functions. Numerically we show that for small arguments the CDFs are well approximated by the lowest orders of this expansion. For the two non-negative random variables, we also compute the moment generating functions in terms of Mei- jer G-functions, and consequently, obtain a Chernoff bound for sums of such random variables. Keywords: Gaussian random variable, product distribution, Meijer G-function, Cher- noff bound, moment generating function AMS subject classifications: 60E99, 33C60, 62E15, 62E17 1. Introduction and motivation Compared to sums of independent random variables, our understanding of products is much less comprehensive. Nevertheless, products of independent random variables arise naturally in many applications including channel modeling [1,2], wireless relaying systems [3], quantum physics (product measurements of product states), as well as signal processing. Here, we are particularly motivated by a tensor sensing problem (see Ref. [4] for the basic idea). In this problem we consider n1×n2×···×n tensors T 2 R d and wish to recover them from measurements of the form yi := hAi;T i 1 2 d j nj with the sensing tensors also being of rank one, Ai = ai ⊗ai ⊗· · ·⊗ai with ai 2 R . Additionally, j we assumed that the entries of ai are iid Gaussian random variables. Applying such maps to arXiv:1711.10516v2 [math.PR] 27 May 2018 properly normalized rank-one tensor results in a product of d Gaussian random variables. Products of independent random variables have already been studied for more than 50 years [5] but are still subject of ongoing research [6{9]. In particular, it was shown that the probability density function of a product of certain independent and identically distributed (iid) random variables from the exponential family can be written in terms of Meijer G-functions [10]. In this work, we characterize cumulative distribution functions (CDFs) and moment generating functions arising from products of iid normal random variables, products of their squares, and products of their absolute values. We provide power-log series expansions of the CDFs of these distributions and demonstrate numerically that low-order truncations of these series provide tight ∗E-mail: [email protected] yE-mail: [email protected] zE-mail: [email protected] Comparison in Prop. 1.1 of true bound and C for N= 3 Comparison in Prop. 1.1 of true bound and C for N= 6 Comparison in Prop. 1.1 of true bound and C for N= 13 3 3 3 1.2 1.2 1 0.9 1 1 0.8 ) ) ) t t t 5 5 0.8 0.8 5 0.7 2 2 2 i i i g g g Q Q Q 0.6 ( ( ( P P 0.6 0.6 P y y y 0.5 t t t i i i l l l i i i b b b a a a 0.4 b b b o o 0.4 0.4 o r r r p p p 0.3 0.2 0.2 true bound 0.2 true bound true bound upper bound C upper bound C upper bound C 3 3 0.1 3 const=1 const=1 const=1 0 0 0 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 0 0.005 0.01 0.015 0.02 0.025 0.03 0.035 0.04 0.045 0.05 t t t QN 2 Figure 1: Comparison of the CDF P( i=1 gi ≤ t) (blue lines) with the bound stated in Proposi- tion1 (red lines) for different values of N. Here, we chose θ for each value t numerically from all possible values between 10−5 and 0:5 − 10−5 with step size 10−5 such that the right hand side in (1) is minimal. approximations. Moreover, we express the moment generating functions of the two latter distribu- tions in terms of Meijer-G functions. We state the corresponding Chernoff bounds, which bound the CDFs of sums of such products. Finally, we find simplified estimates of the Chernoff bounds and illustrate them numerically. 1.1. Simple bound We first state a simple but quite loose bound to the CDF of the product of iid squared standard Gaussian random variables. N Proposition 1. Let fgigi=1 be a set of iid standard Gaussian random variables (i.e., gi ∼ N (0; 1)). Then " N # Y 2 N θ P gi ≤ t ≤ inf Cθ t ; (1) θ2(0;1=2) i=1 where Γ(−θ + 1 ) C = p 2 > 0: θ π2θ 1 2 1 Proof. For θ < 2 the moment generating function of log(gi ) is given by Z 2 −θ log g2 −2θ 1 −2θ − x Ee i = E jgij = p jxj e 2 dx 2π R (2) 2−θ Z 1 1 2−θ Γ(−θ + 1 ) = p z−θ− 2 e−zdz = p 2 ; π 0 π x2 1 where we have used the substitution z = 2 . Note that for θ ≥ 2 the integral diverges. Now, the proposition is a simple consequence of Chernoff bound: N ! N ! Y 2 X 2 P gi ≤ t = P log(gi ) ≤ log t i=1 i=1 N θ log t −θ log g2 ≤ inf e Ee i (3) θ>0 θ N t = π− 2 inf Γ(−θ + 1 )N : 1 2N 2 θ2(0; 2 ) 1Throughout the article, log(x) denotes the natural logarithm of x. 2 Figure1 shows that this bound is indeed quite loose. This holds in particular for values of t that are very small. However, since Proposition1 is based on Chernoff inequality { a tail bound on sums of random variables { one cannot expect good results for those intermediate values. As a matter of fact, the upper bound in (1) becomes slightly larger than the trivial bound P(Y ≤ t) ≤ 1 already for quite small values of t. Deriving a good approximations for such values t and any N is in the focus of the next section. 2. Power-log series expansion for cumulative distribution functions N Throughout the article, we use the following notation. Let N 2 N and denote by fgigi=1 a set of iid standard Gaussian random variables (i.e., gi ∼ N (0; 1), for all i 2 [N]). We denote the random variables considered in this work by N N N Y Y 2 Y X := gi;Y := gi ;Z := jgij: (4) i=1 i=1 i=1 The probability density function of X can be written in terms of Meijer G-functions [10]. We provide a similar representation for the CDF of X, Y , and Z as well as the corresponding power-log series expansion using the theory developed for the more general Fox H-functions [11]. It is worth noting that series of Meijer-G functions have already been extensively studied. For example, in [12] the expansions in series of Meijer G-functions as well as in series of Jacobi and Chebyshev's polynomials have been provided. In this work, we investigate the power-log series expansion of special instances of Meijer-G functions. An advantage of this expansion is that it does not contain any special functions (excpet derivatives of the Gamma function at 1). For the sake of completeness, we give a brief introduction on Meijer G-functions together with some of their properties in AppendixA; see Refs. [6, 10] for more details. The following proposition is a special case of a result by Cook [13, p. 103] which relies on the Mellin transform. However, for this particular case we provide an elementary proof. N Proposition 2 (CDFs in terms of Meijer G-functions). Let fgigi=1 be a set of independent iden- QN tically distributed standard Gaussian random variables (i.e., gi ∼ N (0; 1)) and X := i=1 gi, QN 2 QN Y := i=1 gi , Z := i=1 jgij with N 2 N. Define the function Gα by 1 1 1; 1=2;:::; 1=2 G (z) := 1 − · G0;N+1 z : (5) α α N N+1;1 2 π 2 0 Then, for any t > 0, 2N (X ≤ t) = (X ≥ −t) = G (6) P P 1 t2 2N (Y ≤ t) = G (7) P 0 t 2N (Z ≤ t) = G : (8) P 0 t2 In Ref. [4] we have provided a proof of the above proposition by deriving first a result for the random variable X. The results for random variables Y and Z then follow trivially. For completeness, we derive a proof for a random variable Y in the AppendixB (see Lemma 16). The statements for X and Z are simple consequences of this result, since for t > 0, 2 2 2 P(Z ≤ t) = P(Z ≤ t ) = P(Y ≤ t ) ; (9) 1 1 (X ≤ t) = (2 (X ≤ t)) = ( (X ≤ t) + 1 − (X ≤ −t)) P 2 P 2 P P 1 1 1 = ( (−t ≤ X ≤ t) + 1) = (X2 ≤ t2) + 1 = (Y ≤ t2) + 1 : (10) 2 P 2 P 2 P 3 Now we are ready to present the main result of this section.
Load more

Recommended publications
  • Thompson Sampling on Symmetric Α-Stable Bandits
    Thompson Sampling on Symmetric α-Stable Bandits Abhimanyu Dubey and Alex Pentland Massachusetts Institute of Technology fdubeya, [email protected] Abstract Thompson Sampling provides an efficient technique to introduce prior knowledge in the multi-armed bandit problem, along with providing remarkable empirical performance. In this paper, we revisit the Thompson Sampling algorithm under rewards drawn from α-stable dis- tributions, which are a class of heavy-tailed probability distributions utilized in finance and economics, in problems such as modeling stock prices and human behavior. We present an efficient framework for α-stable posterior inference, which leads to two algorithms for Thomp- son Sampling in this setting. We prove finite-time regret bounds for both algorithms, and demonstrate through a series of experiments the stronger performance of Thompson Sampling in this setting. With our results, we provide an exposition of α-stable distributions in sequential decision-making, and enable sequential Bayesian inference in applications from diverse fields in finance and complex systems that operate on heavy-tailed features. 1 Introduction The multi-armed bandit (MAB) problem is a fundamental model in understanding the exploration- exploitation dilemma in sequential decision-making. The problem and several of its variants have been studied extensively over the years, and a number of algorithms have been proposed that op- timally solve the bandit problem when the reward distributions are well-behaved, i.e. have a finite support, or are sub-exponential. The most prominently studied class of algorithms are the Upper Confidence Bound (UCB) al- gorithms, that employ an \optimism in the face of uncertainty" heuristic [ACBF02], which have been shown to be optimal (in terms of regret) in several cases [CGM+13, BCBL13].
    [Show full text]
  • Constructing Copulas from Shock Models with Imprecise Distributions
    Constructing copulas from shock models with imprecise distributions MatjaˇzOmladiˇc Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia [email protected] Damjan Skuljˇ Faculty of Social Sciences, University of Ljubljana, Slovenia [email protected] November 19, 2019 Abstract The omnipotence of copulas when modeling dependence given marg- inal distributions in a multivariate stochastic situation is assured by the Sklar's theorem. Montes et al. (2015) suggest the notion of what they call an imprecise copula that brings some of its power in bivari- ate case to the imprecise setting. When there is imprecision about the marginals, one can model the available information by means of arXiv:1812.07850v5 [math.PR] 18 Nov 2019 p-boxes, that are pairs of ordered distribution functions. By anal- ogy they introduce pairs of bivariate functions satisfying certain con- ditions. In this paper we introduce the imprecise versions of some classes of copulas emerging from shock models that are important in applications. The so obtained pairs of functions are not only imprecise copulas but satisfy an even stronger condition. The fact that this con- dition really is stronger is shown in Omladiˇcand Stopar (2019) thus raising the importance of our results. The main technical difficulty 1 in developing our imprecise copulas lies in introducing an appropriate stochastic order on these bivariate objects. Keywords. Marshall's copula, maxmin copula, p-box, imprecise probability, shock model 1 Introduction In this paper we propose copulas arising from shock models in the presence of probabilistic uncertainty, which means that probability distributions are not necessarily precisely known. Copulas have been introduced in the precise setting by A.
    [Show full text]
  • Field Guide to Continuous Probability Distributions
    Field Guide to Continuous Probability Distributions Gavin E. Crooks v 1.0.0 2019 G. E. Crooks – Field Guide to Probability Distributions v 1.0.0 Copyright © 2010-2019 Gavin E. Crooks ISBN: 978-1-7339381-0-5 http://threeplusone.com/fieldguide Berkeley Institute for Theoretical Sciences (BITS) typeset on 2019-04-10 with XeTeX version 0.99999 fonts: Trump Mediaeval (text), Euler (math) 271828182845904 2 G. E. Crooks – Field Guide to Probability Distributions Preface: The search for GUD A common problem is that of describing the probability distribution of a single, continuous variable. A few distributions, such as the normal and exponential, were discovered in the 1800’s or earlier. But about a century ago the great statistician, Karl Pearson, realized that the known probabil- ity distributions were not sufficient to handle all of the phenomena then under investigation, and set out to create new distributions with useful properties. During the 20th century this process continued with abandon and a vast menagerie of distinct mathematical forms were discovered and invented, investigated, analyzed, rediscovered and renamed, all for the purpose of de- scribing the probability of some interesting variable. There are hundreds of named distributions and synonyms in current usage. The apparent diver- sity is unending and disorienting. Fortunately, the situation is less confused than it might at first appear. Most common, continuous, univariate, unimodal distributions can be orga- nized into a small number of distinct families, which are all special cases of a single Grand Unified Distribution. This compendium details these hun- dred or so simple distributions, their properties and their interrelations.
    [Show full text]
  • QUANTIFYING EEG SYNCHRONY USING COPULAS Satish G
    QUANTIFYING EEG SYNCHRONY USING COPULAS Satish G. Iyengara, Justin Dauwelsb, Pramod K. Varshneya and Andrzej Cichockic a Dept. of EECS, Syracuse University, NY b Massachusetts Institute of Technology, Cambridge, MA c RIKEN Brain Science Institute, Japan ABSTRACT However, this is not true with other distributions. The Gaussian In this paper, we consider the problem of quantifying synchrony model fails to characterize any nonlinear dependence and higher or- between multiple simultaneously recorded electroencephalographic der correlations that may be present between the variables. Further, signals. These signals exhibit nonlinear dependencies and non- the multivariate Gaussian model constrains the marginals to also Gaussian statistics. A copula based approach is presented to model follow the Gaussian disribution. As we will show in the following the joint statistics. We then consider the application of copula sections, copula models help alleviate these limitations. Following derived synchrony measures for early diagnosis of Alzheimer’s the same approach as in [4], we then evaluate the classification (nor- disease. Results on real data are presented. mal vs. subjects with MCI) performance using the leave-one-out cross validation procedure. We use the same data set as in [4] thus Index Terms— EEG, Copula theory, Kullback-Leibler diver- allowing comparison with other synchrony measures studied in [4]. gence, Statistical dependence The paper is structured as follows. We discuss copula theory and its use in modeling multivariate time series data in Section 2. 1. INTRODUCTION Section 3 describes the EEG data set used in the present analysis and considers the application of copula theory for EEG synchrony Quantifying synchrony between electroencephalographic (EEG) quantification.
    [Show full text]
  • Joint Distributions Math 217 Probability and Statistics a Discrete Example
    F ⊆ Ω2, then the distribution on Ω = Ω1 × Ω2 is the product of the distributions on Ω1 and Ω2. But that doesn't always happen, and that's what we're interested in. Joint distributions Math 217 Probability and Statistics A discrete example. Deal a standard deck of Prof. D. Joyce, Fall 2014 52 cards to four players so that each player gets 13 cards at random. Let X be the number of Today we'll look at joint random variables and joint spades that the first player gets and Y be the num- distributions in detail. ber of spades that the second player gets. Let's compute the probability mass function f(x; y) = Product distributions. If Ω1 and Ω2 are sam- P (X=x and Y =y), that probability that the first ple spaces, then their distributions P :Ω1 ! R player gets x spades and the second player gets y and P :Ω2 ! R determine a product distribu- spades. 5239 tion on P :Ω1 × Ω2 ! R as follows. First, if There are hands that can be dealt to E1 and E2 are events in Ω1 and Ω2, then define 13 13 P (E × E ) to be P (E )P (E ). That defines P on 13 39 1 2 1 2 these two players. There are hands \rectangles" in Ω1×Ω2. Next, extend that to count- x 13 − x able disjoint unions of rectangles. There's a bit of for the first player with exactly x spades, and with 13 − x26 + x theory to show that what you get is well-defined.
    [Show full text]
  • Decision-Making with Heterogeneous Sensors - a Copula Based Approach
    Syracuse University SURFACE Electrical Engineering and Computer Science - Dissertations College of Engineering and Computer Science 2011 Decision-Making with Heterogeneous Sensors - A Copula Based Approach Satish Giridhar Iyengar Syracuse University Follow this and additional works at: https://surface.syr.edu/eecs_etd Part of the Electrical and Computer Engineering Commons Recommended Citation Iyengar, Satish Giridhar, "Decision-Making with Heterogeneous Sensors - A Copula Based Approach" (2011). Electrical Engineering and Computer Science - Dissertations. 310. https://surface.syr.edu/eecs_etd/310 This Dissertation is brought to you for free and open access by the College of Engineering and Computer Science at SURFACE. It has been accepted for inclusion in Electrical Engineering and Computer Science - Dissertations by an authorized administrator of SURFACE. For more information, please contact [email protected]. Abstract Statistical decision making has wide ranging applications, from communications and signal processing to econometrics and finance. In contrast to the classical one source - one receiver paradigm, several applications have been identified in the recent past that require acquiring data from multiple sources or sensors. Information from the multiple sensors are transmitted to a remotely located receiver known as the fusion center which makes a global decision. Past work has largely focused on fusion of information from homogeneous sensors. This dissertation extends the formulation to the case when the local sensors may possess disparate sensing modalities. Both the theoretical and practical aspects of multimodal signal processing are considered. The first and foremost challenge is to ‘adequately’ model the joint statistics of such heterogeneous sensors. We propose the use of copula theory for this purpose. Copula models are general descriptors of dependence.
    [Show full text]
  • Arxiv:2103.03751V1 [Math.PR] 5 Mar 2021 6.6
    ANALYTIC COMBINATORICS OF COMPOSITION SCHEMES AND PHASE TRANSITIONS WITH MIXED POISSON DISTRIBUTIONS CYRIL BANDERIER, MARKUS KUBA, AND MICHAEL WALLNER Abstract. Multitudinous combinatorial structures are counted by generating func- tions satisfying a composition scheme F(z) = G(H(z)). The corresponding asymp- totic analysis becomes challenging when this scheme is critical (i.e., G and H are simultaneously singular). The singular exponents appearing in the Puiseux expan- sions of G and H then dictate the asymptotics. In this work, we first complement results of Flajolet et al. for a full family of singular exponents of G and H. We identify the arising limit laws (for the number of H-components in F) and prove moment convergence. Then, motivated by many examples (random mappings, planar maps, directed lattice paths), we consider a natural extension of this scheme, namely F(z) = G(H(z))M(z). We discuss the number of H-components of a given size in F; this leads to a nice world of limit laws involving products of beta distributions and of Mittag-Leffler distributions. We also obtain continuous to discrete phase transitions involving mixed Poisson distributions, giving an unified explanation of the associated thresholds. We end with extensions of the critical composition scheme to a cycle scheme and to the multivariate case, leading again to product distributions. Applications are presented for random walks, trees (supertrees of trees, increasingly labelled trees, preferential attachment trees), triangular Pólya urns, and the Chinese restaurant process. This article is kindly devoted to Alois Panholzer, on the occasion of his 50th birthday. Contents 1. Introduction2 2.
    [Show full text]
  • Copula Models of Economic Capital for Life Insurance Companies
    Copula Models of Economic Capital for Life Insurance Companies June 2019 2 Copula Models of Economic Capital for Life Insurance Companies AUTHOR Arkady Shemyakin SPONSOR Joint Risk Management Research Huan Zhang Comittee Sydney Benson Regina Burroughs Jessica Mohr University of St. Thomas Caveat and Disclaimer The opinions expressed and conclusions reached by the authors are their own and do not represent any official position or opinion of the Society of Actuaries or its members. The Society of Actuaries makes no representation or warranty to the accuracy of the information Copyright © 2019 by the Society of Actuaries. All rights reserved. Copyright © 2019 Society of Actuaries Copula Models of Economic Capital for Life Insurance Companies Arkady Shemyakin, Huan Zhang, 1 Sydney Benson, Regina Burroughs, and Jessica Mohr 1 University of St. Thomas, USA E–mail: [email protected] Abstract The objective of this project is to construct, select, calibrate and validate a prac- tically applicable copula internal model of economic capital for insurance compa- nies. Copula methodology makes it possible to address multiple dependent risk factors. We identify the relevant set of asset and liability variables, and suggest a copula model for the joint distribution of these variables. Estimates of economic capital can be based on the tails of this joint distribution. Models are implemented in open source software (R and Microsoft EXCEL) and tested using simulated as- set/liability data. The results are presented as a finished software product which can be utilized for customization and direct user application. The novelty of the approach consists in estimating interdependent mortality, morbidity, lapse and in- vestment risks in one multivariate model.
    [Show full text]
  • Graphical Models, Exponential Families, and Variational Inference
    Foundations and Trends ® in sample Vol. xx, No xx (xxxx) 1–294 © xxxx xxxxxxxxx DOI: xxxxxx Graphical models, exponential families, and variational inference Martin J. Wainwright1 and Michael I. Jordan2 1 Department of Statistics, and Department of Electrical Engineering and Computer Science Berkeley 94720, USA, [email protected] 2 Department of Statistics, and Department of Electrical Engineering and Computer Science Berkeley 94720, USA, [email protected] Abstract The formalism of probabilistic graphical models provides a unifying framework for capturing complex dependencies among random vari- ables, and building large-scale multivariate statistical models. Graph- ical models have become a focus of research in many statistical, com- putational and mathematical fields, including bioinformatics, commu- nication theory, statistical physics, combinatorial optimization, signal and image processing, information retrieval and statistical machine learning. Many problems that arise in specific instances—including the key problems of computing marginals and modes of probability distributions—are best studied in the general setting. Working with exponential family representations, and exploiting the conjugate du- ality between the cumulant function and the entropy for exponential families, we develop general variational representations of the prob- lems of computing likelihoods, marginal probabilities and most prob- able configurations. We describe how a wide variety of algorithms— among them sum-product, cluster variational methods, expectation- propagation, mean field methods, and max-product—can all be un- derstood in terms of exact or approximate forms of these variational representations. The variational approach provides a complementary alternative to Markov chain Monte Carlo as a general source of ap- proximation methods for inference in large-scale statistical models.
    [Show full text]
  • On the Product of Two Hypoexponential Random Variables
    BAU Journal - Science and Technology Volume 1 Issue 1 ISSN: 2706-784X Article 7 December 2019 ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES Therrar Kadri Faculty of Sciences, Lebanese International University, Lebanon, [email protected] Khaled Smaili Faculty of Sciences, Lebanese University, Zahle, Lebanon, [email protected] Seifedine Kadry Associate Professor, Faculty of Science, Beirut Arab University, Beirut, Lebanon, [email protected] Ali El-Joubbeh Faculty of Sciences, Lebanese University, Zahle, Lebanon, [email protected] Follow this and additional works at: https://digitalcommons.bau.edu.lb/stjournal Part of the Architecture Commons, Business Commons, Engineering Commons, and the Physical Sciences and Mathematics Commons Recommended Citation Kadri, Therrar; Smaili, Khaled; Kadry, Seifedine; and El-Joubbeh, Ali (2019) "ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES," BAU Journal - Science and Technology: Vol. 1 : Iss. 1 , Article 7. Available at: https://digitalcommons.bau.edu.lb/stjournal/vol1/iss1/7 This Article is brought to you for free and open access by Digital Commons @ BAU. It has been accepted for inclusion in BAU Journal - Science and Technology by an authorized editor of Digital Commons @ BAU. For more information, please contact [email protected]. ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES Abstract In this paper, we consider the product of two independent Hypoexponential distributions which has many applications in sciences and engineering. We find analytically the probability density function, the cumulative distribution function, moment generating function, the reliability function and hazard function, which was proved to be a linear combination of the K distribution. Finally, we will apply our results application in stochastic PERT Network.
    [Show full text]
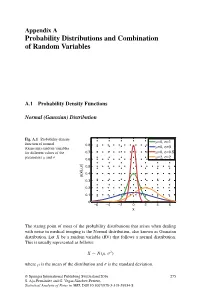
  • Probability Distributions and Combination of Random Variables
    Appendix A Probability Distributions and Combination of Random Variables A.1 Probability Density Functions Normal (Gaussian) Distribution Fig. A.1 Probability density μ σ function of normal =0, =1 0.8 μ σ (Gaussian) random variables =0, =3 for different values of the 0.7 μ=0, σ=0.5 μ σ μ=2, σ=2 parameters and 0.6 ) σ 0.5 , μ 0.4 p(x| 0.3 0.2 0.1 0 −6 −4 −2 0 2 4 6 x The stating point of most of the probability distributions that arises when dealing with noise in medical imaging is the Normal distribution, also known as Gaussian distribution. Let X be a random variable (RV) that follows a normal distribution. This is usually represented as follows: X ∼ N(μ, σ2) where μ is the mean of the distribution and σ is the standard deviation. © Springer International Publishing Switzerland 2016 275 S. Aja-Fernandez´ and G. Vegas-Sanchez-Ferrero,´ Statistical Analysis of Noise in MRI, DOI 10.1007/978-3-319-39934-8 276 Appendix A: Probability Distributions and Combination of Random Variables PDF: (Probability density function) 1 (x − μ)2 p(x|μ, σ) = √ exp − (A.1) σ 2π 2σ2 MGF: (Moment generating function) σ2t2 M (t) = exp μt + X 2 Main parameters: Mean = μ Median = μ Mode = μ Variance = σ2 Main moments: μ1 = E{x}=μ 2 2 2 μ2 = E{x }=μ + σ 3 3 2 μ3 = E{x }=μ + 3μσ 4 4 2 2 4 μ4 = E{x }=μ + 6μ σ + 3σ Rayleigh Distribution Fig.
    [Show full text]
  • Global Warming – Impacts and Future Perspective
    GLOBAL WARMING – IMPACTS AND FUTURE PERSPECTIVE Edited by Bharat Raj Singh Global Warming – Impacts and Future Perspective http://dx.doi.org/10.5772/2599 Edited by Bharat Raj Singh Contributors Juan Cagiao Villar, Sebastián Labella Hidalgo, Adolfo Carballo Penela, Breixo Gómez Meijide, C. Aprea, A. Greco, A. Maiorino, Bharat Raj Singh, Onkar Singh, Amjad Anvari Moghaddam, Gabrielle Decamous, Oluwatosin Olofintoye, Josiah Adeyemo, Fred Otieno, Silvia Duhau, Sotoodehnia Poopak, Amiri Roodan Reza, Hiroshi Ujita, Fengjun Duan, D. Vatansever, E. Siores, T. Shah, Robson Ryu Yamamoto, Paulo Celso de Mello-Farias, Fabiano Simões, Flavio Gilberto Herter, Zsuzsa A. Mayer, Andreas Apfelbacher, Andreas Hornung, Karl Cheng, Bharat Raj Singh, Alan Cheng Published by InTech Janeza Trdine 9, 51000 Rijeka, Croatia Copyright © 2012 InTech All chapters are Open Access distributed under the Creative Commons Attribution 3.0 license, which allows users to download, copy and build upon published articles even for commercial purposes, as long as the author and publisher are properly credited, which ensures maximum dissemination and a wider impact of our publications. After this work has been published by InTech, authors have the right to republish it, in whole or part, in any publication of which they are the author, and to make other personal use of the work. Any republication, referencing or personal use of the work must explicitly identify the original source. Notice Statements and opinions expressed in the chapters are these of the individual contributors and not necessarily those of the editors or publisher. No responsibility is accepted for the accuracy of information contained in the published chapters. The publisher assumes no responsibility for any damage or injury to persons or property arising out of the use of any materials, instructions, methods or ideas contained in the book.
    [Show full text]