DOCSLIB.ORG

Joint Distributions Math 217 Probability and Statistics a Discrete Example

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Joint Distributions Math 217 Probability and Statistics a Discrete Example F ⊆ Ω2, then the distribution on Ω = Ω1 × Ω2 is the product of the distributions on Ω1 and Ω2. But that doesn't always happen, and that's what we're interested in. Joint distributions Math 217 Probability and Statistics A discrete example. Deal a standard deck of Prof. D. Joyce, Fall 2014 52 cards to four players so that each player gets 13 cards at random. Let X be the number of Today we'll look at joint random variables and joint spades that the first player gets and Y be the num- distributions in detail. ber of spades that the second player gets. Let's compute the probability mass function f(x; y) = Product distributions. If Ω1 and Ω2 are sam- P (X=x and Y =y), that probability that the first ple spaces, then their distributions P :Ω1 ! R player gets x spades and the second player gets y and P :Ω2 ! R determine a product distribu- spades. 5239 tion on P :Ω1 × Ω2 ! R as follows. First, if There are hands that can be dealt to E1 and E2 are events in Ω1 and Ω2, then define 13 13 P (E × E ) to be P (E )P (E ). That defines P on 13 39 1 2 1 2 these two players. There are hands \rectangles" in Ω1×Ω2. Next, extend that to count- x 13 − x able disjoint unions of rectangles. There's a bit of for the first player with exactly x spades, and with 13 − x26 + x theory to show that what you get is well-defined. the remaining deck there are Extend to complements of those unions. Again, y 13 − y more theory. Continue by closing under countable hands for the second player with exactly y spades. unions and complements. A lot more theory. But Thus, there are it works. That theory forms part of the the topic 13 39 13 − x26 + x called measure theory which is included in courses on real analysis. x 13 − x y 13 − y When you have the product distribution on Ω1 × ways of dealing hands to those two players with x Ω2, the random variables X and Y are independent, and y spades. Thus, but there are applications where we have a distri- bution on Ω1 × Ω2 that differs from the product 13 39 13 − x26 + x distribution, and for those, X and Y won't be in- x 13 − x y 13 − y f(x; y) = : dependent. That's the situation we'll look at now. 5239 13 13 Definition. A joint random variable (X; Y ) is a random variable on any sample space Ω which is You can write that expression in terms of trino- the product of two sets Ω1 × Ω2. mial coefficients, or in terms of factorials, but we'll Joint random variables do induce probability dis- leave it as it is. If you were a professional Bridge tributions on Ω1 and on Ω2. If E ⊆ Ω1, de- player, you might want to see a table of the values fine P (E) to be the probability in Ω of the set of f(x; y). E × Ω2. That defines P :Ω1 ! R which satisfies It's intuitive that X and Y are not indepen- the axioms for a probability distributions. Simi- dent joint random variables. The more spades the larly, you can define P :Ω2 ! R by declaring for first player has, the fewer the second will proba- F ⊆ Ω2 that P (F ) = P (Ω1 × F ). If it happens bly have. In order to show they're not indepen- that P (E × F ) = P (E)P (F ) for all E ⊆ Ω1 and dent, it's enough to find particular values of x 1 and y so that f(x; y) = P (X=x and Y =y) does We can summarize the cumulative distribution not equal the product of fX (x) = P (X=x) and function as f (y) = P (Y =y). For example, we know they can't Y 8 0 if x < 0 or y < 0 both get 7 spades since there are only 13 spades in > > x2 if 0 ≤ x ≤ 1 and x ≤ y all, so f(7; 7) = 0. But since the first player can get <> F (x; y) = 2xy − y2 if 0 ≤ x ≤ 1 and x > y 7 spades, f (7) > 0, also the second player can, so X > 2y − y2 if x > 1 and 0 ≤ y ≤ 1 f (y) > 0. Therefore f(7; 7) 6= f (7)f (7). We've > Y Y Y :> 1 if x > 1 and y > 1 proven that X and Y are not independent. Generally speaking, joint cumulative distribution A continuous example. Let's choose a point functions aren't used as much as joint density func- from inside a triangle ∆ uniformly at random. Let's tions. Typically, joint c.d.f.'s are much more com- take ∆ to be half the unit square, namely the half plicated to describe, just as in this example. with vertices at (0; 0), (1; 0), and (1; 1). Then Joint distributions and density functions. ∆ = f(x; y) j 0 ≤ y ≤ x ≤ 1g: Density functions are the usual way to describe joint continuous real-valued random variables. 1 The area of this triangle is 2 , so we can find the Let X and Y be two continuous real-valued ran- probability of any event E, a subset of ∆, simply dom variables. Individually, they have their own by doubling its area. The joint probability density cumulative distribution functions 1 function is constantly 2 inside ∆ and 0 outside. FX (x) = P (X ≤ x) FY (y) = P (Y ≤ y); 2 if 0 ≤ y ≤ x ≤ 1 f(x; y) = 0 otherwise whose derivatives, as we know, are the probability density functions A continuous joint random variable (X; Y ) is de- d d termined by its cumulative distribution function f (x) = F (x) f (y) = F (y): X dx X Y dy Y F (x; y) = P (X ≤ x and Y ≤ y): Furthermore, the cumulative distribution functions can be found by integrating the density functions We'll figure out it's value for this example. Z x Z y First, if either x or y is negative, then the event FX (x) = fX (t) dt FY (y) = fY (t) dt: (X ≤ x and Y ≤ y) completely misses the triangle, −∞ −∞ so it's actually empty, so its probability is 0. There is also a joint cumulative distribution func- Second, if x is between 0 and 1 and x ≤ y, then tion for (X; Y ) defined by the event (X ≤ x and Y ≤ y) is a triangle of width 1 2 and height x, so its area is 2 x . Doubling the area F (x; y) = P (X ≤ x and Y ≤ y): gives a probability of x2. Third, if x is between 0 and 1 and x > y, then the The joint probability density function f(x; y) is point (x; y) lies inside the triangle, and the event found by taking the derivative of F twice, once with (X ≤ x and Y ≤ y) is a trapezoid. Its bottom respect to each variable, so that length is x, top length is x − y, and height is y, so @ @ its area is xy − y2=2. Therefore, the probability of f(x; y) = F (x; y): @x @y this event is 2xy − y2. There remain two more cases to be considered, (The notation @ is substituted for d to indicate that but their analyses are omitted. there are other variables in the expression that are 2 held constant while the derivative is taken with respect to the given variable.) The joint cumula- tive distribution function can be recovered from the joint density function by integrating twice Z x Z y F (x; y) = f(s; t) dt ds: −∞ −∞ (When more that one integration is specified, the R y inner integral, namely −∞ f(s; t) dt, is written without parentheses around it, even though the parentheses would help clarify the expression.) Furthermore, the individual cumulative distribu- tion functions are determined by the joint distribu- tion function. FX (x) = P (X ≤ x and Y ≤ 1) = lim F (x; y) = F (x; 1) y!1 FY (y) = P (X ≤ 1 and Y ≤ y) = lim F (x; y) = F (1; y) x!1 The volume under that surface is 1, as it has to be for f to be a probability density function. To find Likewise, the individual density functions can be the probability that (X; Y ) lies in an event E, a found by integrating joint density function. subset of the unit square, just find the volume of Z 1 Z 1 the solid above E and below the surface z = f(x; y). fX (x) = f(x; y) dy; fY (x) = f(x; y) dx −∞ −∞ That's a double integral These individual density functions fX and fy ZZ are often called marginal density functions to dis- P ((X; Y ) 2 E) = f(x; y) dx dy: E tinguish them from the joint density function For example, suppose we want to find the proba- f(X;Y ). Likewise the corresponding individual cu- bility P (0 ≤ X ≤ 3 and 1 ≤ Y ≤ 1). The event mulative distribution functions FX and FY are 4 3 3 1 called marginal cumulative distribution functions to E is (0 ≤ X ≤ 4 and 3 ≤ Y ≤ 1), and that de- scribes a rectangle. The double integral giving the distinguish them form the joint c.d.f F(X;Y ). probability is Another continuous example. The last exam- Z 3=4Z 1 2 ple was a uniform distribution on a triangle.
Load more

Recommended publications
  • Thompson Sampling on Symmetric Α-Stable Bandits
    Thompson Sampling on Symmetric α-Stable Bandits Abhimanyu Dubey and Alex Pentland Massachusetts Institute of Technology fdubeya, [email protected] Abstract Thompson Sampling provides an efficient technique to introduce prior knowledge in the multi-armed bandit problem, along with providing remarkable empirical performance. In this paper, we revisit the Thompson Sampling algorithm under rewards drawn from α-stable dis- tributions, which are a class of heavy-tailed probability distributions utilized in finance and economics, in problems such as modeling stock prices and human behavior. We present an efficient framework for α-stable posterior inference, which leads to two algorithms for Thomp- son Sampling in this setting. We prove finite-time regret bounds for both algorithms, and demonstrate through a series of experiments the stronger performance of Thompson Sampling in this setting. With our results, we provide an exposition of α-stable distributions in sequential decision-making, and enable sequential Bayesian inference in applications from diverse fields in finance and complex systems that operate on heavy-tailed features. 1 Introduction The multi-armed bandit (MAB) problem is a fundamental model in understanding the exploration- exploitation dilemma in sequential decision-making. The problem and several of its variants have been studied extensively over the years, and a number of algorithms have been proposed that op- timally solve the bandit problem when the reward distributions are well-behaved, i.e. have a finite support, or are sub-exponential. The most prominently studied class of algorithms are the Upper Confidence Bound (UCB) al- gorithms, that employ an \optimism in the face of uncertainty" heuristic [ACBF02], which have been shown to be optimal (in terms of regret) in several cases [CGM+13, BCBL13].
    [Show full text]
  • On Products of Gaussian Random Variables
    On products of Gaussian random variables Zeljkaˇ Stojanac∗1, Daniel Suessy1, and Martin Klieschz2 1Institute for Theoretical Physics, University of Cologne, Germany 2 Institute of Theoretical Physics and Astrophysics, University of Gda´nsk,Poland May 29, 2018 Sums of independent random variables form the basis of many fundamental theorems in probability theory and statistics, and therefore, are well understood. The related problem of characterizing products of independent random variables seems to be much more challenging. In this work, we investigate such products of normal random vari- ables, products of their absolute values, and products of their squares. We compute power-log series expansions of their cumulative distribution function (CDF) based on the theory of Fox H-functions. Numerically we show that for small arguments the CDFs are well approximated by the lowest orders of this expansion. For the two non-negative random variables, we also compute the moment generating functions in terms of Mei- jer G-functions, and consequently, obtain a Chernoff bound for sums of such random variables. Keywords: Gaussian random variable, product distribution, Meijer G-function, Cher- noff bound, moment generating function AMS subject classifications: 60E99, 33C60, 62E15, 62E17 1. Introduction and motivation Compared to sums of independent random variables, our understanding of products is much less comprehensive. Nevertheless, products of independent random variables arise naturally in many applications including channel modeling [1,2], wireless relaying systems [3], quantum physics (product measurements of product states), as well as signal processing. Here, we are particularly motivated by a tensor sensing problem (see Ref. [4] for the basic idea). In this problem we consider n1×n2×···×n tensors T 2 R d and wish to recover them from measurements of the form yi := hAi;T i 1 2 d j nj with the sensing tensors also being of rank one, Ai = ai ⊗ai ⊗· · ·⊗ai with ai 2 R .
    [Show full text]
  • Constructing Copulas from Shock Models with Imprecise Distributions
    Constructing copulas from shock models with imprecise distributions MatjaˇzOmladiˇc Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia [email protected] Damjan Skuljˇ Faculty of Social Sciences, University of Ljubljana, Slovenia [email protected] November 19, 2019 Abstract The omnipotence of copulas when modeling dependence given marg- inal distributions in a multivariate stochastic situation is assured by the Sklar's theorem. Montes et al. (2015) suggest the notion of what they call an imprecise copula that brings some of its power in bivari- ate case to the imprecise setting. When there is imprecision about the marginals, one can model the available information by means of arXiv:1812.07850v5 [math.PR] 18 Nov 2019 p-boxes, that are pairs of ordered distribution functions. By anal- ogy they introduce pairs of bivariate functions satisfying certain con- ditions. In this paper we introduce the imprecise versions of some classes of copulas emerging from shock models that are important in applications. The so obtained pairs of functions are not only imprecise copulas but satisfy an even stronger condition. The fact that this con- dition really is stronger is shown in Omladiˇcand Stopar (2019) thus raising the importance of our results. The main technical difficulty 1 in developing our imprecise copulas lies in introducing an appropriate stochastic order on these bivariate objects. Keywords. Marshall's copula, maxmin copula, p-box, imprecise probability, shock model 1 Introduction In this paper we propose copulas arising from shock models in the presence of probabilistic uncertainty, which means that probability distributions are not necessarily precisely known. Copulas have been introduced in the precise setting by A.
    [Show full text]
  • Field Guide to Continuous Probability Distributions
    Field Guide to Continuous Probability Distributions Gavin E. Crooks v 1.0.0 2019 G. E. Crooks – Field Guide to Probability Distributions v 1.0.0 Copyright © 2010-2019 Gavin E. Crooks ISBN: 978-1-7339381-0-5 http://threeplusone.com/fieldguide Berkeley Institute for Theoretical Sciences (BITS) typeset on 2019-04-10 with XeTeX version 0.99999 fonts: Trump Mediaeval (text), Euler (math) 271828182845904 2 G. E. Crooks – Field Guide to Probability Distributions Preface: The search for GUD A common problem is that of describing the probability distribution of a single, continuous variable. A few distributions, such as the normal and exponential, were discovered in the 1800’s or earlier. But about a century ago the great statistician, Karl Pearson, realized that the known probabil- ity distributions were not sufficient to handle all of the phenomena then under investigation, and set out to create new distributions with useful properties. During the 20th century this process continued with abandon and a vast menagerie of distinct mathematical forms were discovered and invented, investigated, analyzed, rediscovered and renamed, all for the purpose of de- scribing the probability of some interesting variable. There are hundreds of named distributions and synonyms in current usage. The apparent diver- sity is unending and disorienting. Fortunately, the situation is less confused than it might at first appear. Most common, continuous, univariate, unimodal distributions can be orga- nized into a small number of distinct families, which are all special cases of a single Grand Unified Distribution. This compendium details these hun- dred or so simple distributions, their properties and their interrelations.
    [Show full text]
  • QUANTIFYING EEG SYNCHRONY USING COPULAS Satish G
    QUANTIFYING EEG SYNCHRONY USING COPULAS Satish G. Iyengara, Justin Dauwelsb, Pramod K. Varshneya and Andrzej Cichockic a Dept. of EECS, Syracuse University, NY b Massachusetts Institute of Technology, Cambridge, MA c RIKEN Brain Science Institute, Japan ABSTRACT However, this is not true with other distributions. The Gaussian In this paper, we consider the problem of quantifying synchrony model fails to characterize any nonlinear dependence and higher or- between multiple simultaneously recorded electroencephalographic der correlations that may be present between the variables. Further, signals. These signals exhibit nonlinear dependencies and non- the multivariate Gaussian model constrains the marginals to also Gaussian statistics. A copula based approach is presented to model follow the Gaussian disribution. As we will show in the following the joint statistics. We then consider the application of copula sections, copula models help alleviate these limitations. Following derived synchrony measures for early diagnosis of Alzheimer’s the same approach as in [4], we then evaluate the classification (nor- disease. Results on real data are presented. mal vs. subjects with MCI) performance using the leave-one-out cross validation procedure. We use the same data set as in [4] thus Index Terms— EEG, Copula theory, Kullback-Leibler diver- allowing comparison with other synchrony measures studied in [4]. gence, Statistical dependence The paper is structured as follows. We discuss copula theory and its use in modeling multivariate time series data in Section 2. 1. INTRODUCTION Section 3 describes the EEG data set used in the present analysis and considers the application of copula theory for EEG synchrony Quantifying synchrony between electroencephalographic (EEG) quantification.
    [Show full text]
  • Decision-Making with Heterogeneous Sensors - a Copula Based Approach
    Syracuse University SURFACE Electrical Engineering and Computer Science - Dissertations College of Engineering and Computer Science 2011 Decision-Making with Heterogeneous Sensors - A Copula Based Approach Satish Giridhar Iyengar Syracuse University Follow this and additional works at: https://surface.syr.edu/eecs_etd Part of the Electrical and Computer Engineering Commons Recommended Citation Iyengar, Satish Giridhar, "Decision-Making with Heterogeneous Sensors - A Copula Based Approach" (2011). Electrical Engineering and Computer Science - Dissertations. 310. https://surface.syr.edu/eecs_etd/310 This Dissertation is brought to you for free and open access by the College of Engineering and Computer Science at SURFACE. It has been accepted for inclusion in Electrical Engineering and Computer Science - Dissertations by an authorized administrator of SURFACE. For more information, please contact [email protected]. Abstract Statistical decision making has wide ranging applications, from communications and signal processing to econometrics and finance. In contrast to the classical one source - one receiver paradigm, several applications have been identified in the recent past that require acquiring data from multiple sources or sensors. Information from the multiple sensors are transmitted to a remotely located receiver known as the fusion center which makes a global decision. Past work has largely focused on fusion of information from homogeneous sensors. This dissertation extends the formulation to the case when the local sensors may possess disparate sensing modalities. Both the theoretical and practical aspects of multimodal signal processing are considered. The first and foremost challenge is to ‘adequately’ model the joint statistics of such heterogeneous sensors. We propose the use of copula theory for this purpose. Copula models are general descriptors of dependence.
    [Show full text]
  • Arxiv:2103.03751V1 [Math.PR] 5 Mar 2021 6.6
    ANALYTIC COMBINATORICS OF COMPOSITION SCHEMES AND PHASE TRANSITIONS WITH MIXED POISSON DISTRIBUTIONS CYRIL BANDERIER, MARKUS KUBA, AND MICHAEL WALLNER Abstract. Multitudinous combinatorial structures are counted by generating func- tions satisfying a composition scheme F(z) = G(H(z)). The corresponding asymp- totic analysis becomes challenging when this scheme is critical (i.e., G and H are simultaneously singular). The singular exponents appearing in the Puiseux expan- sions of G and H then dictate the asymptotics. In this work, we first complement results of Flajolet et al. for a full family of singular exponents of G and H. We identify the arising limit laws (for the number of H-components in F) and prove moment convergence. Then, motivated by many examples (random mappings, planar maps, directed lattice paths), we consider a natural extension of this scheme, namely F(z) = G(H(z))M(z). We discuss the number of H-components of a given size in F; this leads to a nice world of limit laws involving products of beta distributions and of Mittag-Leffler distributions. We also obtain continuous to discrete phase transitions involving mixed Poisson distributions, giving an unified explanation of the associated thresholds. We end with extensions of the critical composition scheme to a cycle scheme and to the multivariate case, leading again to product distributions. Applications are presented for random walks, trees (supertrees of trees, increasingly labelled trees, preferential attachment trees), triangular Pólya urns, and the Chinese restaurant process. This article is kindly devoted to Alois Panholzer, on the occasion of his 50th birthday. Contents 1. Introduction2 2.
    [Show full text]
  • Copula Models of Economic Capital for Life Insurance Companies
    Copula Models of Economic Capital for Life Insurance Companies June 2019 2 Copula Models of Economic Capital for Life Insurance Companies AUTHOR Arkady Shemyakin SPONSOR Joint Risk Management Research Huan Zhang Comittee Sydney Benson Regina Burroughs Jessica Mohr University of St. Thomas Caveat and Disclaimer The opinions expressed and conclusions reached by the authors are their own and do not represent any official position or opinion of the Society of Actuaries or its members. The Society of Actuaries makes no representation or warranty to the accuracy of the information Copyright © 2019 by the Society of Actuaries. All rights reserved. Copyright © 2019 Society of Actuaries Copula Models of Economic Capital for Life Insurance Companies Arkady Shemyakin, Huan Zhang, 1 Sydney Benson, Regina Burroughs, and Jessica Mohr 1 University of St. Thomas, USA E–mail: [email protected] Abstract The objective of this project is to construct, select, calibrate and validate a prac- tically applicable copula internal model of economic capital for insurance compa- nies. Copula methodology makes it possible to address multiple dependent risk factors. We identify the relevant set of asset and liability variables, and suggest a copula model for the joint distribution of these variables. Estimates of economic capital can be based on the tails of this joint distribution. Models are implemented in open source software (R and Microsoft EXCEL) and tested using simulated as- set/liability data. The results are presented as a finished software product which can be utilized for customization and direct user application. The novelty of the approach consists in estimating interdependent mortality, morbidity, lapse and in- vestment risks in one multivariate model.
    [Show full text]
  • Graphical Models, Exponential Families, and Variational Inference
    Foundations and Trends ® in sample Vol. xx, No xx (xxxx) 1–294 © xxxx xxxxxxxxx DOI: xxxxxx Graphical models, exponential families, and variational inference Martin J. Wainwright1 and Michael I. Jordan2 1 Department of Statistics, and Department of Electrical Engineering and Computer Science Berkeley 94720, USA, [email protected] 2 Department of Statistics, and Department of Electrical Engineering and Computer Science Berkeley 94720, USA, [email protected] Abstract The formalism of probabilistic graphical models provides a unifying framework for capturing complex dependencies among random vari- ables, and building large-scale multivariate statistical models. Graph- ical models have become a focus of research in many statistical, com- putational and mathematical fields, including bioinformatics, commu- nication theory, statistical physics, combinatorial optimization, signal and image processing, information retrieval and statistical machine learning. Many problems that arise in specific instances—including the key problems of computing marginals and modes of probability distributions—are best studied in the general setting. Working with exponential family representations, and exploiting the conjugate du- ality between the cumulant function and the entropy for exponential families, we develop general variational representations of the prob- lems of computing likelihoods, marginal probabilities and most prob- able configurations. We describe how a wide variety of algorithms— among them sum-product, cluster variational methods, expectation- propagation, mean field methods, and max-product—can all be un- derstood in terms of exact or approximate forms of these variational representations. The variational approach provides a complementary alternative to Markov chain Monte Carlo as a general source of ap- proximation methods for inference in large-scale statistical models.
    [Show full text]
  • On the Product of Two Hypoexponential Random Variables
    BAU Journal - Science and Technology Volume 1 Issue 1 ISSN: 2706-784X Article 7 December 2019 ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES Therrar Kadri Faculty of Sciences, Lebanese International University, Lebanon, [email protected] Khaled Smaili Faculty of Sciences, Lebanese University, Zahle, Lebanon, [email protected] Seifedine Kadry Associate Professor, Faculty of Science, Beirut Arab University, Beirut, Lebanon, [email protected] Ali El-Joubbeh Faculty of Sciences, Lebanese University, Zahle, Lebanon, [email protected] Follow this and additional works at: https://digitalcommons.bau.edu.lb/stjournal Part of the Architecture Commons, Business Commons, Engineering Commons, and the Physical Sciences and Mathematics Commons Recommended Citation Kadri, Therrar; Smaili, Khaled; Kadry, Seifedine; and El-Joubbeh, Ali (2019) "ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES," BAU Journal - Science and Technology: Vol. 1 : Iss. 1 , Article 7. Available at: https://digitalcommons.bau.edu.lb/stjournal/vol1/iss1/7 This Article is brought to you for free and open access by Digital Commons @ BAU. It has been accepted for inclusion in BAU Journal - Science and Technology by an authorized editor of Digital Commons @ BAU. For more information, please contact [email protected]. ON THE PRODUCT OF TWO HYPOEXPONENTIAL RANDOM VARIABLES Abstract In this paper, we consider the product of two independent Hypoexponential distributions which has many applications in sciences and engineering. We find analytically the probability density function, the cumulative distribution function, moment generating function, the reliability function and hazard function, which was proved to be a linear combination of the K distribution. Finally, we will apply our results application in stochastic PERT Network.
    [Show full text]
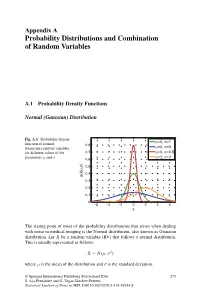
  • Probability Distributions and Combination of Random Variables
    Appendix A Probability Distributions and Combination of Random Variables A.1 Probability Density Functions Normal (Gaussian) Distribution Fig. A.1 Probability density μ σ function of normal =0, =1 0.8 μ σ (Gaussian) random variables =0, =3 for different values of the 0.7 μ=0, σ=0.5 μ σ μ=2, σ=2 parameters and 0.6 ) σ 0.5 , μ 0.4 p(x| 0.3 0.2 0.1 0 −6 −4 −2 0 2 4 6 x The stating point of most of the probability distributions that arises when dealing with noise in medical imaging is the Normal distribution, also known as Gaussian distribution. Let X be a random variable (RV) that follows a normal distribution. This is usually represented as follows: X ∼ N(μ, σ2) where μ is the mean of the distribution and σ is the standard deviation. © Springer International Publishing Switzerland 2016 275 S. Aja-Fernandez´ and G. Vegas-Sanchez-Ferrero,´ Statistical Analysis of Noise in MRI, DOI 10.1007/978-3-319-39934-8 276 Appendix A: Probability Distributions and Combination of Random Variables PDF: (Probability density function) 1 (x − μ)2 p(x|μ, σ) = √ exp − (A.1) σ 2π 2σ2 MGF: (Moment generating function) σ2t2 M (t) = exp μt + X 2 Main parameters: Mean = μ Median = μ Mode = μ Variance = σ2 Main moments: μ1 = E{x}=μ 2 2 2 μ2 = E{x }=μ + σ 3 3 2 μ3 = E{x }=μ + 3μσ 4 4 2 2 4 μ4 = E{x }=μ + 6μ σ + 3σ Rayleigh Distribution Fig.
    [Show full text]
  • Global Warming – Impacts and Future Perspective
    GLOBAL WARMING – IMPACTS AND FUTURE PERSPECTIVE Edited by Bharat Raj Singh Global Warming – Impacts and Future Perspective http://dx.doi.org/10.5772/2599 Edited by Bharat Raj Singh Contributors Juan Cagiao Villar, Sebastián Labella Hidalgo, Adolfo Carballo Penela, Breixo Gómez Meijide, C. Aprea, A. Greco, A. Maiorino, Bharat Raj Singh, Onkar Singh, Amjad Anvari Moghaddam, Gabrielle Decamous, Oluwatosin Olofintoye, Josiah Adeyemo, Fred Otieno, Silvia Duhau, Sotoodehnia Poopak, Amiri Roodan Reza, Hiroshi Ujita, Fengjun Duan, D. Vatansever, E. Siores, T. Shah, Robson Ryu Yamamoto, Paulo Celso de Mello-Farias, Fabiano Simões, Flavio Gilberto Herter, Zsuzsa A. Mayer, Andreas Apfelbacher, Andreas Hornung, Karl Cheng, Bharat Raj Singh, Alan Cheng Published by InTech Janeza Trdine 9, 51000 Rijeka, Croatia Copyright © 2012 InTech All chapters are Open Access distributed under the Creative Commons Attribution 3.0 license, which allows users to download, copy and build upon published articles even for commercial purposes, as long as the author and publisher are properly credited, which ensures maximum dissemination and a wider impact of our publications. After this work has been published by InTech, authors have the right to republish it, in whole or part, in any publication of which they are the author, and to make other personal use of the work. Any republication, referencing or personal use of the work must explicitly identify the original source. Notice Statements and opinions expressed in the chapters are these of the individual contributors and not necessarily those of the editors or publisher. No responsibility is accepted for the accuracy of information contained in the published chapters. The publisher assumes no responsibility for any damage or injury to persons or property arising out of the use of any materials, instructions, methods or ideas contained in the book.
    [Show full text]